大型圆柱滚子轴承滚动体素线形状对端面圆跳动检测值的影响

郑国胜，吴迎清

（1. 铁道部驻哈尔滨车辆验收室，黑龙江 哈尔滨 150036；2. 哈尔滨轴承集团公司 铁路轴承制造分厂，黑龙江 哈尔滨150036）

1 前言

大型圆柱滚子轴承是大型机械设备使用的重要部件之一，其质量的好坏直接影响到主机的性能及安全性。大型圆柱滚子轴承通常承受的载荷非常大，而且工作环境恶劣，所以如何提高其承载能力和使用寿命也就非常重要。为了降低边缘效应，防止应力集中，滚动体一般采用圆弧、直线加圆弧修形及对数曲线等形状。由于滚动体素线为圆弧形状，当以圆弧素线为基准测量滚子端面圆跳动时，造成测量值偏大，所测数值不是真实数值。本文就圆弧素线影响滚子端面圆跳动测量值展开讨论，并提出了解决办法。

2 滚子端面圆跳动测量存在的问题

图1 中，滚动体滚动面（φ32mm尺寸所标注的圆柱表面）素线方程：Y=3.58×10-3ln〔1/［1-（2X/49.2）2］〕，其中X≠49.2/2。素线是由两条满足此方程的彼此对称的对数曲线所组成。

该轴承滚动体的加工工艺如下：

1.棒料锯断→2.毛坯车成型→3.热处理→4.粗磨外径→5.粗磨端面→6.细磨外径→7.细磨端面→8.硬车倒角→9.精磨外径→10.精磨端面→11.终磨外径→12.尺寸分组→13.精研外径→14.磁粉探伤15.光饰→16.超精外径→17.清洗→18外观→19.尺寸分组→20.涂油包装→21.终检验收。

在检验过程中发现，端面圆跳动合格的滚动体，经“超精外径”工序加工之后，端面圆跳动变得不合格了。

图1 某轴承滚动体的相关技术要求

“超精外径”工序加工前后比较，除滚动体直径有变化外，滚动体滚动面的素线形状也与加工前的不同。经“超精外径”工序加工后，素线形状由加工前的直线变成了对数曲线。

工艺中其它的外径加工工序，如：“终磨外径”、“精磨外径”等，虽然加工前后，滚动体直径同样有变化，但素线形状却没变（加工前后都是直线）。这些工序加工后，没有出现类似于“超精外径”工序加工后的测量问题，因此，素线形状是导致出现端面圆跳动测量问题的原因。

滚动面素线形状对滚动体端面圆跳动测量的影响，有必要进行深入的分析。

3 对数形素线对测量端面圆跳动影响的定性分析

测量滚动体端面圆跳动使用的仪器是C742型轴承检测专用仪器。检测时，被测滚动体的滚动面被置于“支撑三角台”的两个倾斜面上，滚动体滚动面与两倾斜面呈线接触状态，实现了径向的定位；在滚动体轴向上，用“轴向定位快”加以单方向定位。图2 给出测量时被测滚动体、支撑三角台、轴向定位快、检测仪表的相互位置关系。

测量时，滚动体必须被旋转一周以上，并记录下滚动体旋转过程中千分表示值的最大和最小值。最大和最小值的差值，就是滚动体的端面圆跳动数值。

图2 滚动体端面跳动测量示意图

采用图2 的测量定位方式，当滚动体滚动表面的素线是直线时，测量时对被测滚动体施以向下和向“轴向定位块”方向力时，滚动体只剩下一个自由度——绕自身轴线的转动，因而，测量的结果是准确的。

图3 轴承滚动体的素线比例图

如前所述，该轴承滚动体滚动面的素线，在“精研外径”工序后，由直线变成了两条相对称的对数曲线组合曲线，其单条曲线方程：Y=3.58×10-3ln〔1/［1-（2X/49.2）2］〕。素线形状的比例图见图3。

由于滚动体的素线呈现图3曲线的形状。因此，其滚动表面与图2 中“支撑三角台”的两个倾斜支撑面，不像直素线滚动体那样呈直线接触，而是呈点接触的状态。

按图2，滚动体在被施加向下和向“轴向定位块”方向的力时，被测滚动体实际上有2个自由度：一个是绕其自身轴线的转动，另一个是在垂直平面内，绕其与“支撑三角台”两支撑面支撑点的转动。

由于存在着绕支撑点转动的现象，测值必然存在误差。导致了端面圆跳动合格的滚动体，在“超精外径”工序加工之后，变得不合格了。

4 对数形素线对测量端面圆跳动影响的定量分析

测量中，由于被测滚动体承受的法向力不超过20N，径向定位面（“支撑三角台”的两倾斜面）与滚动体的滚动面之间的弹性变形可以忽略。因此，可以认为被测滚动体与“支撑三角台”的两倾斜支撑面间，是相切的位置关系。

当径向支撑点位于滚动体轴向的不同横截面上时，“支撑三角台”的倾斜支撑面与滚动体轴线的夹角是不同的。

从素线方程Y=3.58×10-3l n〔1/［1-（2X/49.2）2］〕出发，可以得出径向支撑点在滚动体轴向的不同横截面上时，支撑面与滚动体轴线间的夹角。其公式如下（推导过程略）：

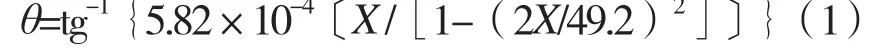
其中：θ——滚动体轴线与“支撑三角台”支撑面间的夹角；

X——滚动体支撑点所在的轴向横截面与滚子轴向中截面间的距离。

由公式（1）可知，当X=0时、θ=0；当X≠0时、θ≠0。即除支撑点位于中截面外，位于任意横截面上，被测滚动体的轴线都会与水平面存在夹角。

被测滚动体的轴线与水平面间的夹角可以用下述公式计算（推导过程略）：

其中：α——滚动体轴线与水平面间的夹角；

θ——滚动体的轴线与“支撑三角台”支撑面间的夹角；

γ——“支撑三角台”两倾斜支撑面间的夹角。

从表1 是按公式（1）和（2）计算后得出的支撑点在不同位置时，滚动体的轴线与水平面间的夹角（γ取60°），计算过程略。

表1 支撑点所在的横截面与中截面间间距和滚动体轴线与水平面间夹角的对应表

表1 得出，支撑点离中截面越远，滚动体轴线与水平面夹角越大。按图2 测量时，不可能控制住支撑点位置，也就是测量过程中滚动体的轴线存在着摆动现象。

轴线的摆动对端面圆跳动测值的影响，可以用下述公式计算（推导过程略）。

其中：δ——轴线摆动对端面跳动测值的影响值；

R——测量端面跳动时测点距滚动体端面中心的距离；

α——滚动体轴线与水平面的夹角。

滚动体轴线摆动对端面圆跳动测值的最大影响值计算如下：

（1）实际测量操作时，支撑点与滚动体中截面的距离不会超过6mm。取X=6mm。

（2）测量端面圆跳动时，测量点要求尽量靠近滚动体的端面倒角边缘。由图1可知，滚动体的端面上的倒角最大值为1.4mm，滚动体直径φ32mm。因而，R=32/2-1.4=14.6（mm）。考虑到实际应用，取R=14mm。

将X=6mm、R=14mm代入公式（3），计算得：δmax=0.103mm。

计算结果反应出：素线是对数曲线时，按图2 的测量方法，会产生很大的误差。

5 解决方法

从定性和定量的分析结果看，该轴承滚动体在“超精外径”工序加工之后，图2 的端面圆跳动测量方法不再适用了。

当采取措施，消除检测时滚动体在垂直平面内绕其与“支撑三角台”的两倾斜支撑面上支撑点的转动现象，被测滚动体就仅存绕其自身轴线的转动的一个自由度，可实现测量的准确性。

理论上采用径向的两点定位方式，可限制滚动体在垂直平面内的转动。

图4 是最简单的改进方法之一。对 原有“支撑三角台”作了改进，在“支撑三角台”的中部开出槽。由于中部带槽，被测滚动体的滚动面与“支撑三角台”槽的边缘相接触，相当于每侧斜面有两个接触点，消除了测量过程中滚动体在垂直面内摆动现象。

此改进不仅使原有测量方式得以继续沿用，而且直接用原“支撑三角台”进行改进，加工简单、成本低。同时，对带有直线性素线的滚动体，可以直接应用。

通过100粒样本的试验证明，改进之后，消除了改进之前存在的测量误差。

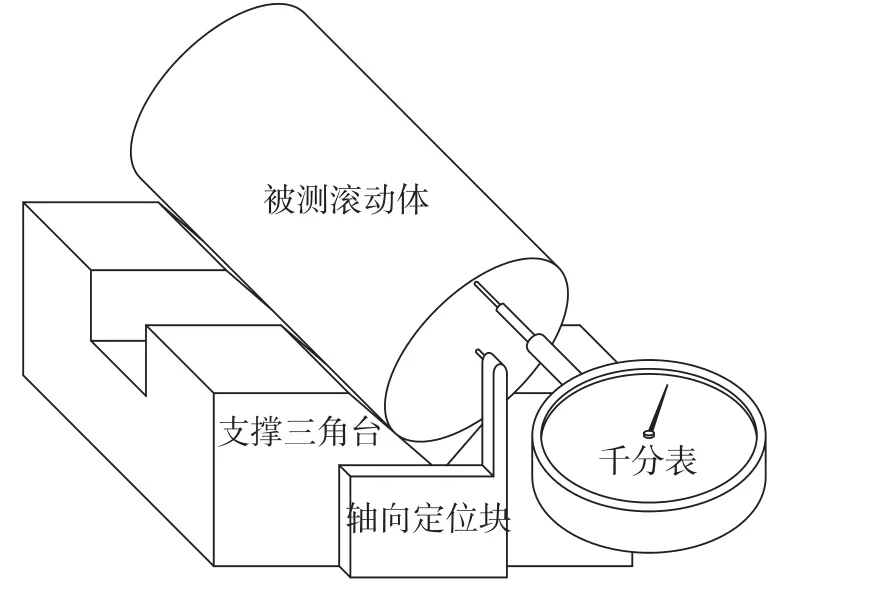
图4 改进后的滚动体端面跳动测量示意图

6 结束语

在超精外径加工之后（素线加工成对数曲线后），该轴承滚动体滚动面素线形状，由直线变为对数曲线，不能采用原有的检测手段。

由于存在着绕径向支撑点转动的现象，测值必然存在误差，且误差很大。

为消除滚动面素线形状所带来的测量误差，采用对“支撑三角台”中部加槽的方法，最简单、有效。

无论何种方式，采用径向支撑面的两点支撑，就可以消除对数形素线滚动体绕支撑点转动的现象，实现对滚动体端面圆跳动的准确测量。