应用数理统计方法减少偏心轴承内孔加工误差

薛 萍，陈立萍，娄志鹏

（1. 哈尔滨哈轴精密轴承制造有限公司，黑龙江 哈尔滨 150036；2.哈尔滨轴承配件有限公司 滚子制造分厂，黑龙江哈尔滨150036；3. 哈尔滨市精密特种轴承厂，黑龙江 哈尔滨150036）

1 前言

统计分析法是以现场观察与实际测量所得的数据为基础，应用概率论和统计学原理，确定在一定加工条件下，一批零件加工误差的大小及其分布情况，这种方法既可以识别系统误差的大小与方向，也可识别各种随机误差因素对加工精度的综合影响，由于这种方法是建立在对大量实测数据进行统计的基础上，故非常适用于轴承零件的生产。

2 加工误差的统计分析

统计分析方法是通过测量一批零件加工后的实际尺寸，作出尺寸分布曲线，然后按此曲线的位置（相对于理想尺寸）和形状（分散范围）判断这种加工方法产生误差的性质和大小。

以下通过铰削加工偏心轴承PTU120一批尺寸为φ12±0.01mm孔的例子，介绍尺寸分布及其应用。若使用 的铰刀，并保持切削用量不便，设铰削后测得孔径尺寸接近正态分布，其值xi见数据表1 。

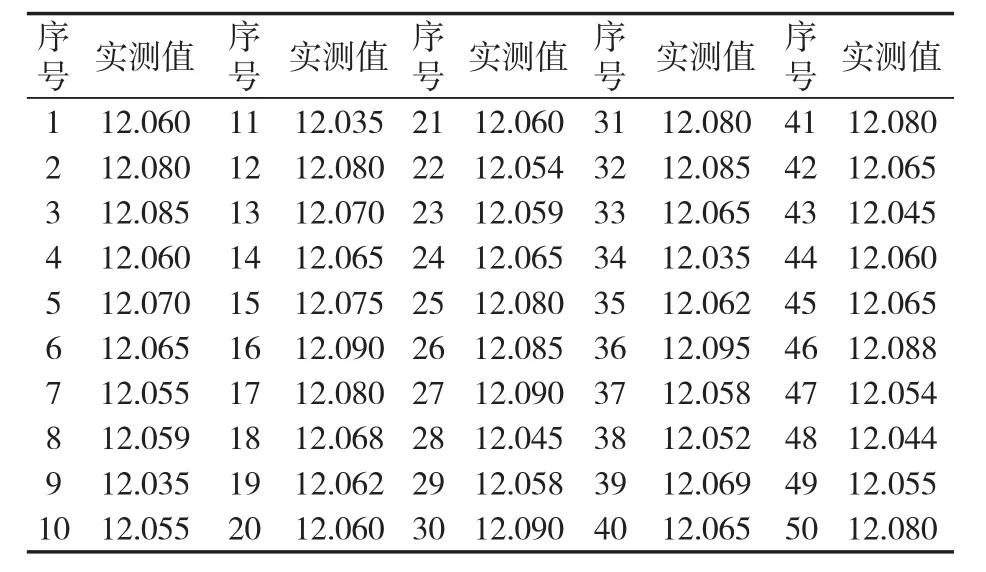
表1 孔径尺寸实测数据/mm

2.1 计算孔的平均尺寸x

按下式球样本平均值：

式中，xi——各实测尺寸,

n——实测零件的总数。

由上面所给的实测数据可求得 x=12.080mm。

2.2 计算常值系统误差

在加工误差接近正态分布的情况下，常值系统误差实际上是实测尺寸算术平均值相对于理想尺寸的偏移值，可表示为：

式中，xm——工件的理想尺寸，即公差带中心值,

由此可计算得本例的常值系统误差为0.08mm,这说明每个零件孔的直径尺寸与设计要求的平均尺寸都有0.08mm的误差存在，常值系统误差决定正态分布曲线的位置，此误差一般可以通过对工艺系统进行适当的调整来消除或减小。

2.3 计算随机误差

在加工误差接近正态分布的条件下，通常以一批零件尺寸的分散范围代表随机误差的大小，即：

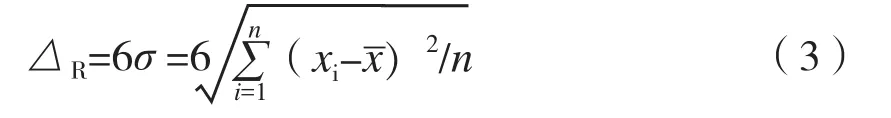
本例中，由所测数据计算可得：

△R=6×0.0067mm≈0.04mm

随机误差以平均尺寸为中心，有正有负对称分布，其大小决定了正态分布曲线的形状。

3 确定工序能力系数

可以用工序能力系数Cp来表示工序能力的大小。当加工误差接近正态分布时，工序能力系数按下式计算：

根据工序能力系数Cp的大小，可将工序能力分为五个等级，见表2。一般情况下，工序能力不应低于2级，即要求Cp＞1。

需要指出的是，Cp＞1只说明工序能力足够，但并不能保证所加工的零件均是合格品。若存在较大的常值或变值系统误差，仍可能出现不合格品。为此，又引入实际工艺能力系数Cpk:

表2 工序能力等级

工序能力系数Cp表示工艺过程本身的能力，而实际工艺能力系数Cpk则表示工艺过程满足加工质量要求的能力，实际上是对“工艺过程能力”和“质量控制能力”的综合，两者侧重点不同，常需同时加以考虑。

4 计算不合格率

通过分布曲线不仅可以掌握某道工序随机误差的分布范围，而且还可根据分布曲线和公差带之间的相对位置得知不同误差范围的内出现的零件数占全部零件数的百分比，估算在采用调整法加工时产生不合格品的可能性及其数量。

在通常情况下，计算不合格品率需要同时考虑常值系统误差和随机误差。仍以前述孔加工要求为例，若改进后加工这批零件得到：则由变换：

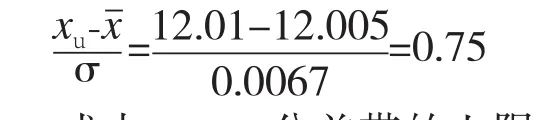
式中，xu—公差带的上限。可查标准正态分布曲线值表有：F（z）=0.2730。可求出尺寸过大的不合格品率为：

0.5-0.2730 =0.2270

同理，可求出尺寸过小的不合格品率，得：

表3 孔径尺寸实测数据/mm

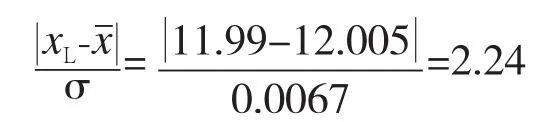
式中，xL—公差带的下限。

可查标准正态分布曲线值表对应的F（z）=0.4874，可求出尺寸过小的不合格率为

0.5-0.4874 =0.0126

则总不合格率为：0.2270+0.0126=0.2396，即23.96%。

5 减少不合格品的措施

依据尺寸分布图和公差带要求，减少不合格品率有以下主要措施：

5.1 消除常值系统误差

本例中孔的加工尺寸要求为φ12±0.01mm，即公差T=0.02mm。由前述实测并计算得知，铰孔工序的随机误差6σ=6×0.067mm=0.04mm，而改进前其常值系统误差已达0.08mm（图1），也就是说所加工的零件均为不合格品，即不合格率100%。

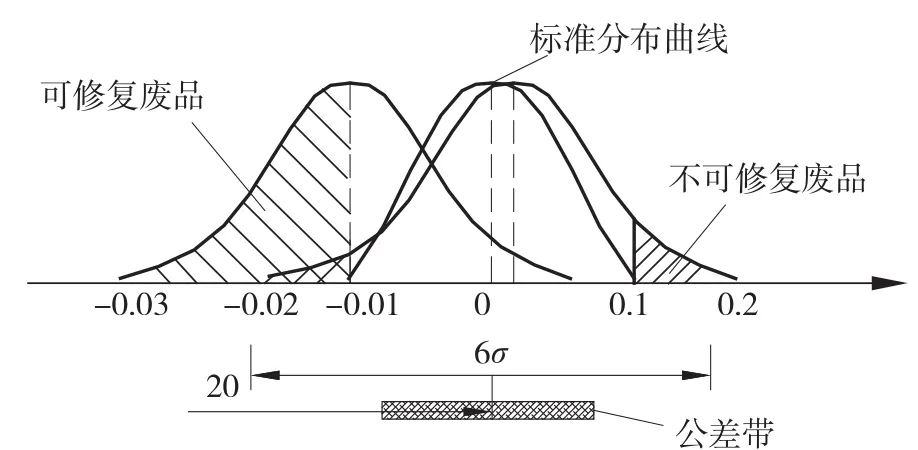
图1 尺寸调整前后的不合格品率

为减少不合格品数量，首先应考虑消除常值系统误差，本例中就是将铰刀直径磨小0.08mm，在其铰孔是常值误差为零，如图2 所示的右边一条曲线。但此时由于工艺系统的随机误差大于零件的公差，即6σ＞T，故仍会产生不合格品。由Z=1.5，查标准正态分布曲线值表可得F（z）=0.4332，故超出公差带以外的过大尺寸（对孔加工来说是不可修复品）、过小尺寸（对孔加工来说是可修复品）的不合格率均为0.5-0.4332=0.0668，即总的不合格品率降低为13.36%。

5.2 提高工序能力

有针对性地采取相应的工艺措施，如选择精度更高的机床、改变工艺参数、调整工序安排等，是工艺系统的随机误差6σ减小，也即使工序能力提高，从而减小不合格品率。

5.3 增大不合格品的可修复性

根据图1 所示尺寸分布曲线，若在消除常值系统误差的基础上将铰刀直径再磨小0.01mm，也就是将分布中心调整到比公差带中心小0.01mm，如图2 所示左边的一条分布曲线，就不会出现不可修复废品，而只有尺寸过小的可修复废品，此时可知可修复的合格品率为97%。

6 结束语

根据统计数据，分析加工误差的存在形式，及时调整机床和加工状态，此方法分析研究加工误差的缺点是，需在全部工件加工之后，才能绘制出分布曲线，故不能反映出零件的加工先后顺序。

【1】于惠力，向敬忠，张春宜.机械设计.科学出版社，2007.

【2】张世昌，李旦，高航.机械制造技术基础.高等教育出版社，2007.

【3】成大先主编.机械设计手册.化学工业出版社，2007.

【4】彭志源主编.最新机械工程师应用技术与机械构造设计参数及计算方法应用手册.银声音像出版社,2005.