基于相关向量机的赖氨酸反应过程参数软测量

嵇小辅，张孟尧，王博，黄丽

（江苏大学 电气信息工程学院，江苏 镇江212013）

赖氨酸发酵过程是一个多变量、非线性、强耦合的复杂动态过程 .目前使用的测量方法主要是在线取样，离线分析的方法，存在较大的测量延时，难以实施在线实时控制，同时在线取样容易引入人为污染，降低发酵过程品质.在现有技术条件下，一些直接反映发酵品质的基质浓度、菌体浓度、产物浓度等关键生物量参数目前还缺乏在线实时测量的仪器与手段，成为制约在线控制的技术瓶颈.软测量是利用在线可测的辅助变量对难以在线测量的主导变量进行在线估计的技术，是解决生物反应过程测量瓶颈的有效途径.生物反应过程的软测量建模有很多方法，大体可分为机理建模、黑箱建模和混合建模三大类.黑箱建模是基于过程数据，采用数据拟合回归方法建立软测量模型.文献［1-4］分别提出了采用标准支持向量机（SVM）建立了赖氨酸反应过程的软测量模型，以及基于模糊最小二乘支持向量机、聚类动态最小二乘支持向量机、粒子群最小二乘支持向量机等软测量方法.为了解决支持向量机实际应用时存在的难题［5］，Michael提出一种与支持向量机相似的稀疏概率模型，即相关向量机（RVM），其训练在贝叶斯框架下进行，克服了支持向量机的上述所有缺点，已被证实在回归精度、泛化能力等方面优于前者.本文将RVM引入赖氨酸反应过程的软测量，建立基质浓度、菌体浓度、产物浓度等不可直接测量参量的软测量模型，实现了赖氨酸反应过程不可直接测量的关键参量的在线实时测量.

1 相关向量机原理

给定训练数据样本集｛xi，ti其中xi∈Rn是输入变量，ti∈R是与xi对应的输出变量，是回归过程中的真实值.假设输出变量全部由带有白噪声的回归模型产生，即有

式（1）中：样本噪声εi满足均值为0，方差为σ2的高斯分布，即εi～N（ε｜0，σ2）.

与SVM类似，RVM将回归函数表示成基函数K（x，xi）的线性组合形式，即

式（2）中：ω＝［ω0，ω1，…，ωM］T是可调的权重向量；ω0是回归函数中的偏置.由于噪声εi满足高斯分布，由式（1）可知：ti也满足于均值y（xi；ω），方差σ2的高斯分布，即

为了描述方便起见，引入超参数β＝1／σ2，则整个训练数据集的似然函数为

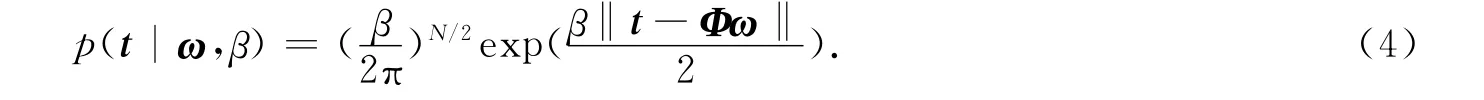
式（4）中：t＝［t1，t2，…，tN］T；Φ∈RN×（N+1）是设计矩阵，定义为Φ＝［Φ1（x1），Φ（x2），…，Φ（xN）］T；基函数向量Φ（xi）＝［1，K（xi，x1），…，K（xi，xN）T］，i＝1，2，…，N，即

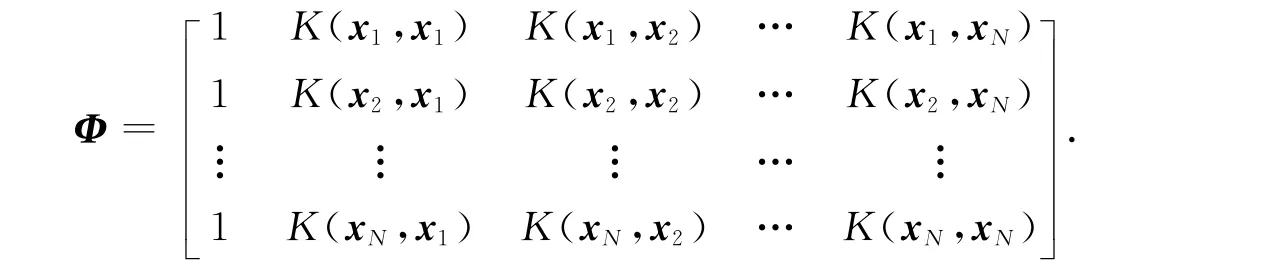
RVM训练过程的目标是求取权值向量ω的后验分布.为了保证模型稀疏性，需要定义权值ωi的先验分布.假设ωi满足均值为0，方差为α-1j的高斯分布，则ω的先验可以表示为

式（5）中：α＝［α0，α1，…，αN］T每个独立的超参数αj只与其对应的权值ωj相关.根据贝叶斯公式，利用样本似然函数（4）和ω先验分布（5）可得ω的后验分布为

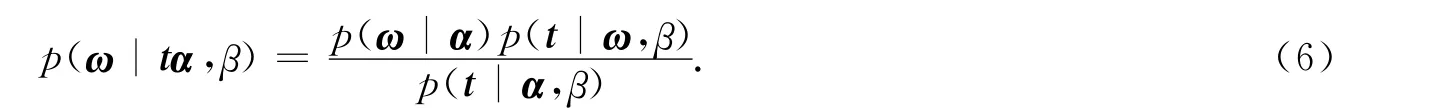
由于p（ω｜α）和p（t｜ω，β）均满足高斯分布，因此其乘积p（ω｜α）p（t｜ω，β）也满足高斯分布，而p（t｜ω，β）不含有参数ω，可以看作是归一化系数，所以ω的后验能进一步表示为

其协方差均值为

而其均值为

式（9）中：A＝diag｛α0，α1，…，αN｝.

可以看出，超参数β和αj直接影响ω的后验分布，需要对其进行优化，从而获得ω的最大后验分布.优化过程可以依据贝叶斯证据框架，通过最大化边缘似然p（ω｜α，β）取负对数得到目标函数，然后令目标函数分别对超参数αj和β求偏导并令偏导数为0而得到 .即

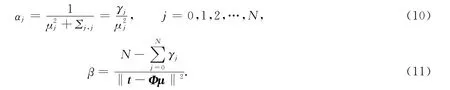
式（10），（11）中：μj为权值后验均值向量μ的第j个元素；Σj，j为协方差矩阵Σ的第j个对角元素；γj＝1-αjΣj，j.在RVM模型训练过程中，式（8）～（11）要依次迭代计算，直到所有参数都收敛或者达到最大收敛次数为止，这时可认为RVM建模过程完成.

2 赖氨酸反应过程软测量模型构建

赖氨酸软测量模型的精度和泛化能力与软测量模型输入数据的预处理有很大关系.为了消除测量噪声，首先对输入数据采用巴特沃思滤波器进行滤波处理，产生一个平滑的样本数据.同时，由于各变量的变化范围差别很大，因此采用最大最小值归一化方法对数据进行归一化处理，将原始数据映射到区间［0，1］内，即

式（12）中：xs，i为标准化数据，xi为原始数据；maxxi和minxi分别为原始数据的最大值和最小值.

基于滤波和归一化处理后的数据，对RVM模型进行学习训练，由此可以看出，RVM学习过程是基于贝叶斯框架对权重的后验分布进行推理的过程 .具体算法有如下6个主要步骤：1）初始化超级参数αi，i＝1，2，…，M；2）计算权重后验分布的均值μ和方差Σ；3）计算γi，i＝1，2，…，M，再估计αi，i＝1，2，…，M；4）重复步骤2），3），直到所有的超级参数都收敛；5）由于αi＝∞对应的权重均值为μi＝0，删除其对应的权重；6）对于新的输入数据x，通过收敛的αMP和σ2MP对目标数据进行预测，所采用的预测分布函数为

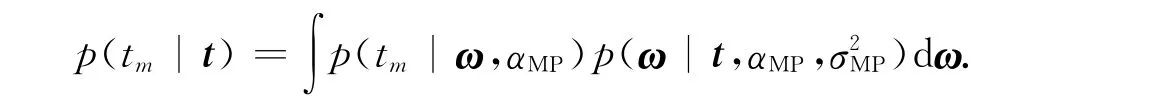
3 仿真结果与分析

针对实验室的WKT型生物反应器，以L-赖氨酸流加发酵过程为对象进行实验研究 .为使实验过程能客观反映实际生产过程，对实验和建模过程进行设计.

1）根据前期对赖氨酸反应过程的机理和数据分析，赖氨酸反应过程的基质浓度、菌体浓度、产物浓度的软测量模型与溶解氧值、发酵液pH值、二氧化碳释放率、氧吸收率和葡萄糖流加速率等参量紧密相关 .因此，选择上述变量为RVM软测量模型的输入变量.

2）每批次发酵周期72h，采样周期为15min，通过测试仪器对溶解氧值、发酵液pH值、二氧化碳释放率、氧吸收率、葡萄糖流加速率等参量进行实时采集，每2min取样并离线化验得到基质质量浓度ρ（基质）、菌体质量浓度ρ（菌体）、产物质量浓度ρ（产物）的值 .其中：菌体质量浓度采用细胞干重法计算得到，即取10mL发酵液于离心管中，在3 000r·min-1下离心5min，弃上清，蒸馏水洗涤2次，在105℃干燥至恒质量后称量；基质质量浓度采用SBA-40C型多功能生物传感器测定；产物质量浓度采用改进的茚三酮比色法进行测定，即取上清液2mL加茚三酮试剂4mL混合，沸水浴加热20min，冷却后通过分光分度计测定475mm处的吸光度值，通过查标准L-赖氨酸曲线得到.

3）考虑5个批次培养以检验赖氨酸反应过程的RVM软测量模型，每批次间的初始条件设为不同，补料策略亦有相应变化，以增强各批次间的差异性 .发酵罐罐压控制在0～0.25MPa，发酵罐罐温控制在（（0～50）±0.5）℃，发酵前搅拌电机转速为400r·min-1时标定溶解氧电极的基准读数，其中前4批次发酵数据作为训练样本集，离线训练获得RVM软测量模型，第5个批次用于检验RVM软测量模型的泛化能力.

采用训练好的RVM模型对第5批数据进行泛化能力检验.基质质量浓度基质质量浓度ρ（基质）、菌体质量浓度ρ（菌体）、产物质量浓度ρ（产物）的预测曲线，如图1～3所示 .从图1～3可以看出：所建立的RVM模型具有拟合精度高、泛化能力强的优点.

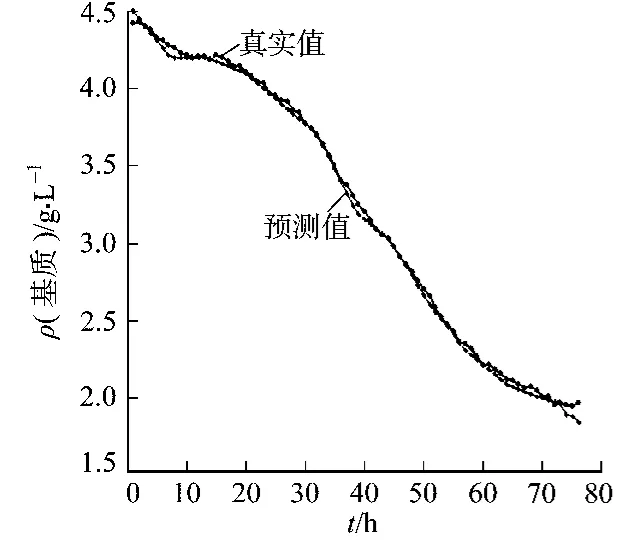
图1 基质浓度预测曲线图Fig.1 Predicted value of glucose concentration

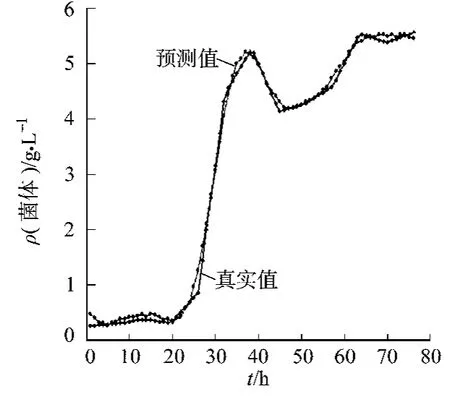
图2 菌体浓度预测曲线Fig.2 Predicted value of cell concentration

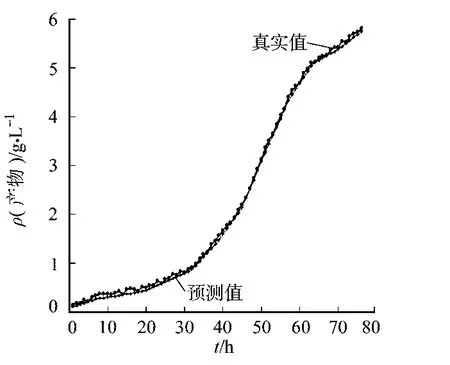
图3 产物浓度预测曲线Fig.3 Predicted value of product concentration

4 结论

在分析赖氨酸反应过程特性的基础上，提出一种基于相关向量机的赖氨酸反应过程基质浓度、菌体浓度和产物浓度的软测量模型.由于采用贝叶斯方法进行概率预测，相对于支持向量机稀疏性更好，所需要的核函数向量个数更少，因此测试时间更短，可以实现赖氨酸反应过程的实时、在线测量.

［1］ 孙玉坤，陈明忠，嵇小辅，等.基于支持向量机的赖氨酸发酵生物参数软测量［J］.仪器仪表学报，2008，29（10）：2067-2071.

［2］ 王博，嵇小辅，孙玉坤.基于自适应模糊支持向量机的L-赖氨酸发酵过程建模研究［J］.仪器仪表学报，2010，31（8）：467-481.

［3］ 王博，孙玉坤，嵇小辅，等.基于 PSO-SVM 逆的L-赖氨酸发酵过程软测量方法［J］.化工学报，2012，26（3）：224-227.

［4］ 孙玉坤，王博，黄永红，等.基于聚类动态LS-SVM 的L-赖氨酸发酵过程软测量方法［J］.仪器仪表学报，2010，24（2）：1024-1028.

［5］ TIPPING M E.Sparse Bayesian learning and the relevance vector machine［J］.Journal of Machine Learning Research，2001，1（3）：211-244.