一种基于非线性系统的直接加权优化辨识算法

姚杰，朱永红

（景德镇陶瓷学院 机械电子工程学院，江西 景德镇333403）

系统辨识只是利用数学的方法，从输入、输出观测数据序列中提炼出对象的数学模型，为控制器的设计作充分的模型准备基础.根据系统对象模型的类别，可将系统辨识的理论研究分为线性系统辨识和非线性系统辨识.线性系统辨识的研究较为成熟，已有现成的理论分析基础和系统辨识仿真软件可直接调用［1-10］；而非线性系统的辨识研究也正日益开展.文献［7］对多种特殊的非线性系统展开研究，如Wiener系统、Hammerstein系统和二者之间的任意组合形式，提出了诸如最小概率法、互方差辅助变量法、盲极大似然法等多种辨识方法.文献［10］分析了正交基函数的构造方法，即当采用所构造的正交基函数形式来表示原非线性系统时，有限脉冲响应模型、Laruerre模型和双参数Kautz模型都可以作为该正交基函数模型结构的特例.文献［3］中提出了一种新的非线性系统辨识方法——直接加权优化法.文献［4］将直接加权优化辨识方法的基本思想应用于对分段仿射系统中各个权重值的辨识 .文献［5］分析了直接加权优化辨识法对某参数的摄动所带来的影响 .本文在文献［3］的思想基础之上，进行直接加权优化辨识方法的研究.

1 问题描述

给定观测数据｛φ（t），y（t），其非线性系统可描述为

式（1）中：f0（φ（t））称为未知待辨识估计的非线性系统函数，φ（t）为回归矢量 .通常情况下，φ（t）有两种形式分别对应于非线性有限脉冲响应形式和外部输入下的非线性自回归形式，即

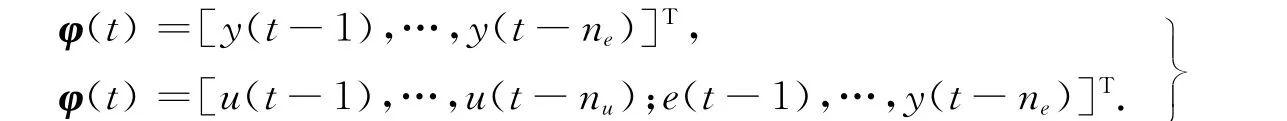
其中：e（t）为零均值的独立同分布的随机白噪声，对应的方差值记为σ2e.

设非线性系统f0（φ（t））的一个逼近线性仿射函数形式为

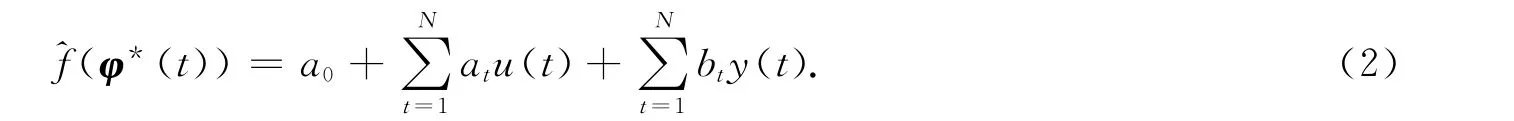
将式（2）与文献［3］中对应的式子相对比，可知式（2）增加了N个关于输入观测数据序列｛u（t）的线性项，从而增加了N个待求解的未知权重值.由此可见，文献［3］中的线性仿射函数形式是本文中的特例，其中特殊之处在于本文中所有的全取为零值.

因此，文中以下内容的目的就在于如何确定出由这2N+1个未知权重值构成的参数矢量θ.即

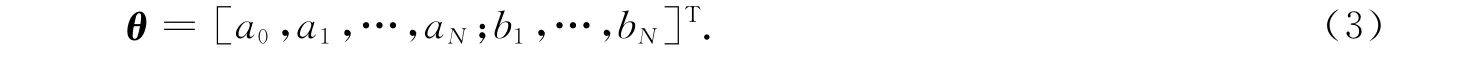
2 直接加权优化辨识

为了能够在任意指定点φ＊（t）处都得到良好的逼近程度，用（φ＊（t））来近似地逼近原非线性系统f0（φ（t）），逼近的准确度依赖于权重值和的选取 .则建立衡量逼近性能的目标函数为

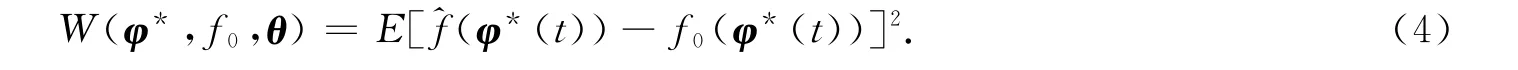
将式（2）代入到式（4）中，可得

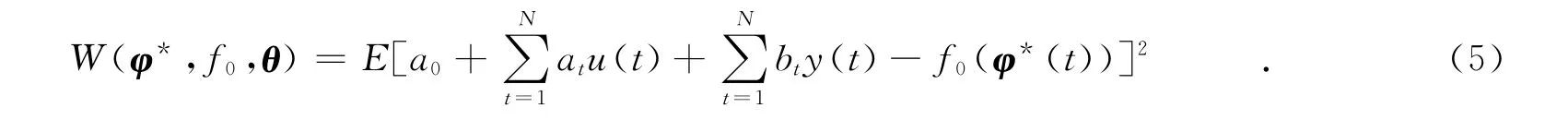
将式（1）代入式（5）中，可得展开后的目标函数为

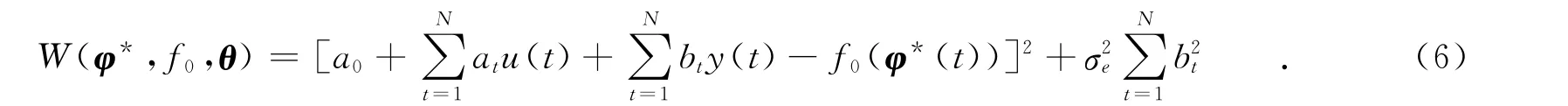
式（6）中的数学期望运算过程利用了噪声e（t）为独立同分布的白噪声假设条件，并且白噪声e（t）与输入、输出观测数据序列｛u（t），y（t）均为不相关.引入符号表示（t）＝φ（t）-φ＊（t）后，在式（6）中进行增加和减去相同的两项，等式不变，可得

式（7）中得到的平方项即为通常的平方偏差，后一项为由未建模引起的方差误差项.从式（7）可看出：偏差项将会变得任意大，除非增加关于权重值的两个约束条件在上述两个施加的约束条件下，式（7）的目标函数可以简化为

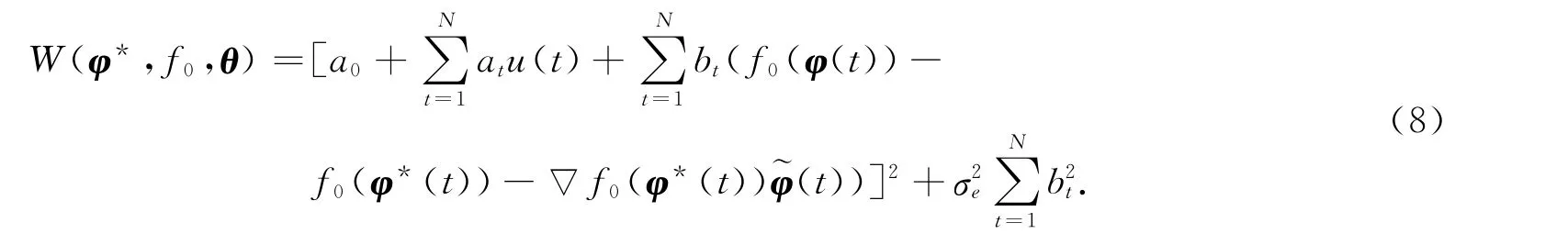
利用泰勒级数公式，将非线性系统f0（φ（t））在f0（φ＊）处展开得

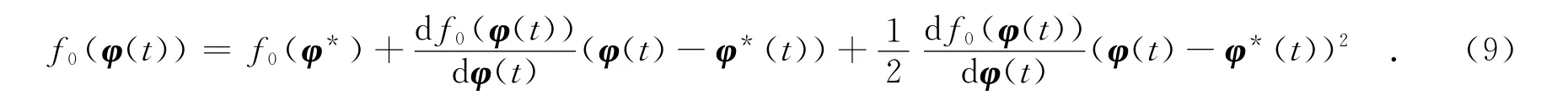
假设非线性函数f0满足Lipschitz条件，即

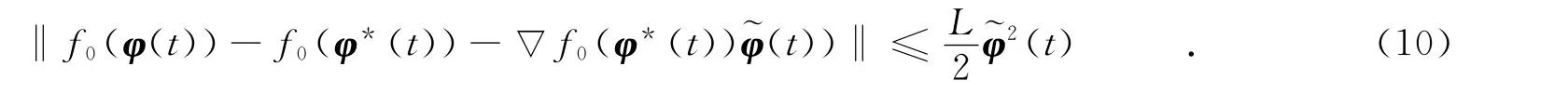
式（10）中：L为一常数 .联合以上三式可得到式（10）均方误差期望的一个上界值为

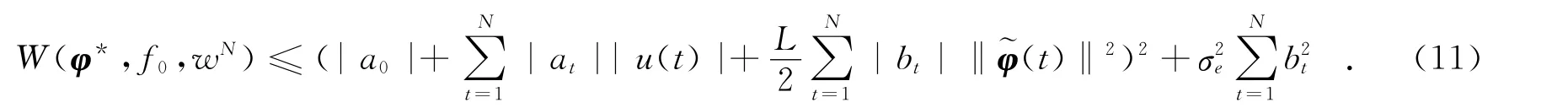
直接加权优化辨识算法中的最小化均方误差期望值W（φ＊，f0，wN），可转化为最小化式（11）右边的上界值，即得到的最优化问题为

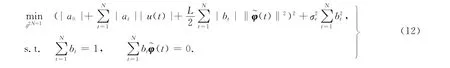
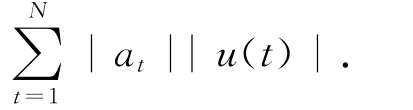
3 最优Karush-Kuhn-Tucker充要条件

为了从式（12）所示的带有约束条件的最优化问题中求解出未知权重值组成的未知参数矢量θ，引入松弛变量st，wt，使得｜bt｜≤st，t＝1，2，…，N；｜at｜≤wt，t＝0，1，…，N.将引入的两松弛变量st，wt应用于最优化问题式（12）中，可得最优化问题为

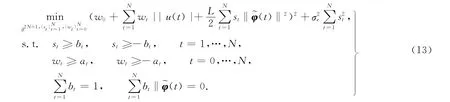
要想得到最优化问题式（13）的最优解（a0，a1，…，aN；b1，…，bN；st｜N1，wt｜），根据最优 Karush-Kuhn-Tucker充要条件可知，对应的拉格朗日函数为

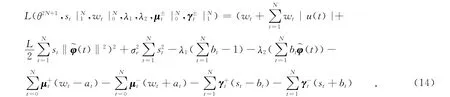
利用Karush-Kuhn-Tucker最优性充要条件，可得在最优处存在成立的等式，即

在最优解除包含有隐含的最优等式，｜bt｜＝st，t＝1，2，…，N；｜at｜＝wt，t＝0，1，…，N，故由第1个子式可知＝.在第9个子式中，若at＞0，则wt+at＝｜at｜+at＝2at＞0，要使第9个子式成立必须有，从而由第1个子式有，＝＝0.在第2个子式中，若at＜0，则wt-at＝｜at｜-at＝-2at＞0.同理要使得第8个子式成立，需要使得＝0.从而由第1个子式有＝＝0.当at＝0时即所有的输入观测数据序列前的未知权重值都为0，在线性仿射函数形式中仅剩下输出观测数据序列项，从而简化为文献［3］中的特殊形式.

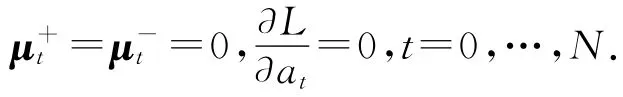
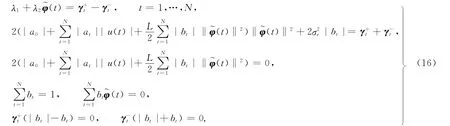
式（16）中：第4个和第5个子式所代表的等式关系已全部隐含在所构造的拉格朗日函数之中 .将第3个子式代入第2个子式中可得

当bt＞0时，由式（16）的第7个子式可得｜bt｜+bt＝2bt＞0.从而要使第7个子式成立，需要有γ-t＝0.将＝0代入到式（16）的第1个子式，可得

再代入到式（17）即有

同理考虑当bt＜0时，有

将式（18）代入式（16）的第3个子式，可得

若在实数域中，必然有等式

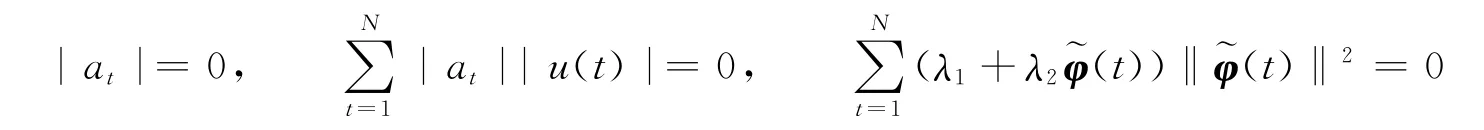
成立 .由此可解得

但这并不是此处所期望得到的结果.为此扩展到复数域中，考虑到

的｜u（t）｜表示的是输入激励信号的振幅值，当选择恒定振幅值的输入激励信号时，有｜u（t）｜＝k（k为一正常数）.因此，式（19）可改写为

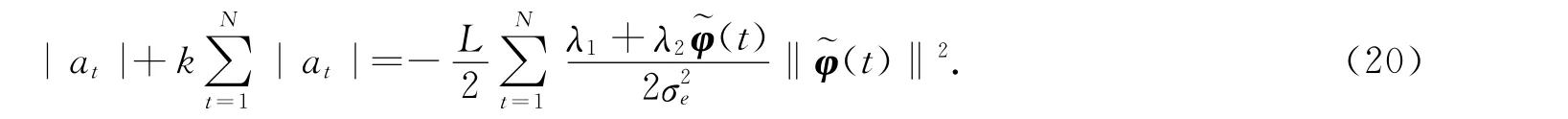
满足以上等式的未知权重值的选取方法有无穷多种，如

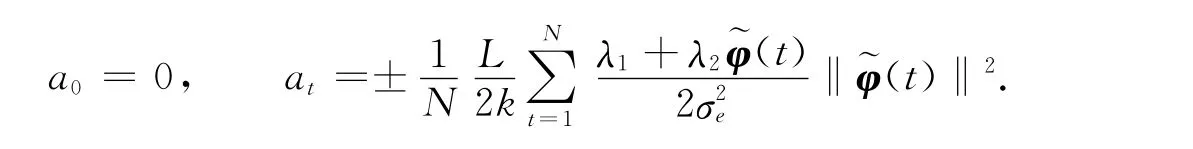
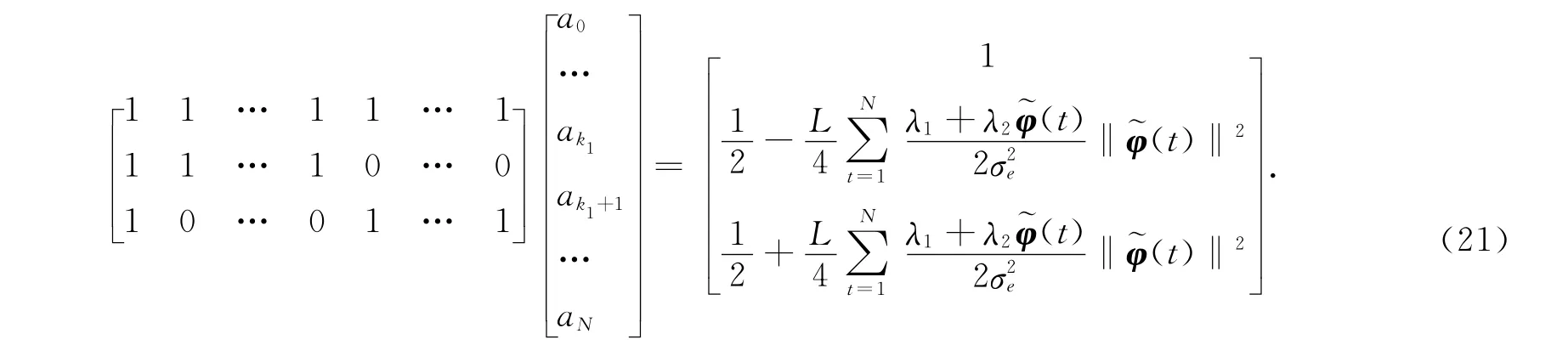
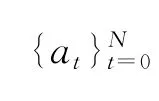
4 未知权重值的迭代求解

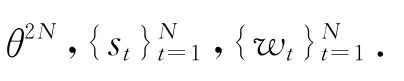
设上式左边4N×4N维的矩阵记为A，右边0表示4N×1维的零矢量，则不等式约束条件可简记为Aη≥0.同理，可将两等式约束条件简记为矩阵乘积的形式

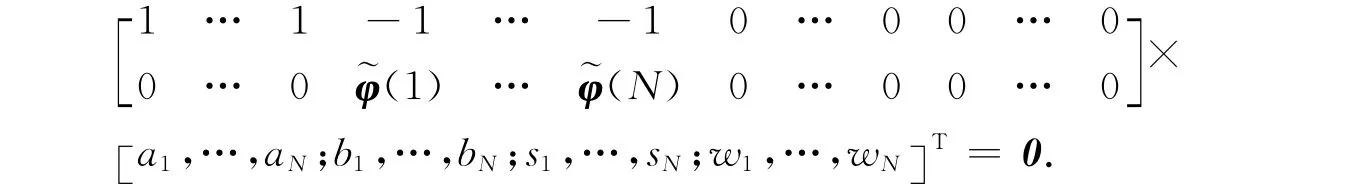
设上式左边2×4N维矩阵记为B，右边0表示2×1的零矢量，则等式约束条件可记为Bη＝0.

下面对目标函数进行整理 .很明显目标函数的第2项可改写为

而目标函数中第1项括号内的式子可改写成

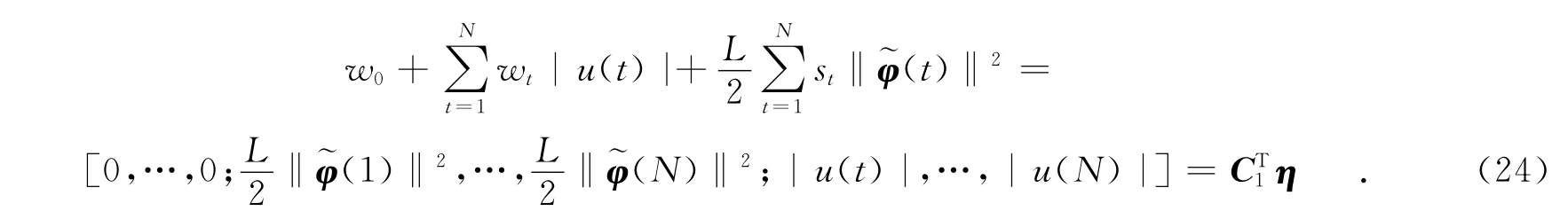
将式（24）平方后可得

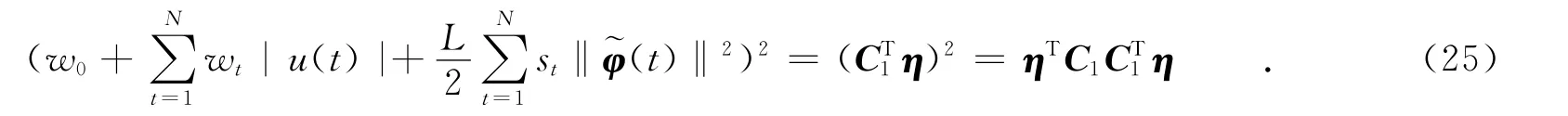
由此可构成最优化问题为

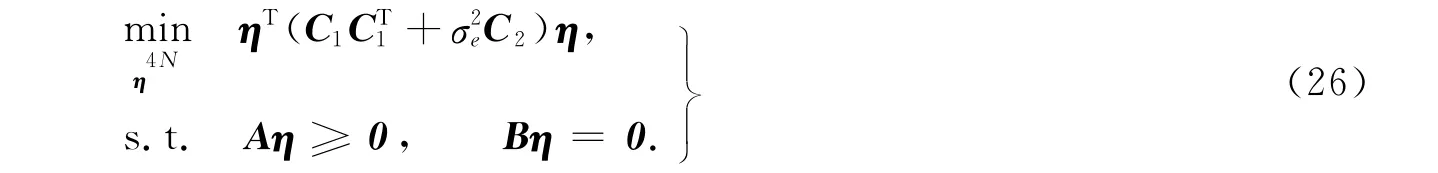
很明显，式（26）所表示的最优化问题中的目标函数为关于优化变量η的二次函数，不等式约束和等式约束均为关于优化变量η的线性函数.即式（26）为一个二次规划问题，可采用内点法迭代地求解.定义式（26）的拉格朗日函数为

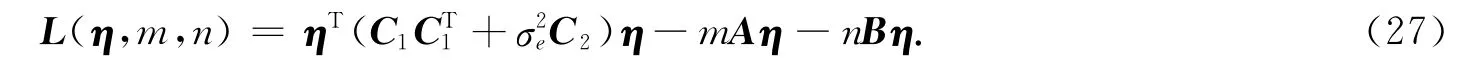
对式（27）关于η求偏导，可得

为了消去Aη≥0不等式约束中的不等号，引入一个松弛变量z≥0，对以上各式进行改写为

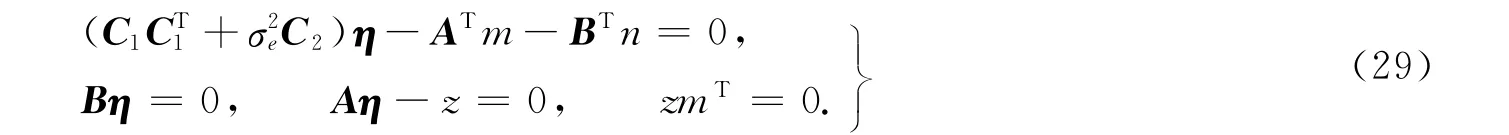
设由式（29）构成的矩阵记为

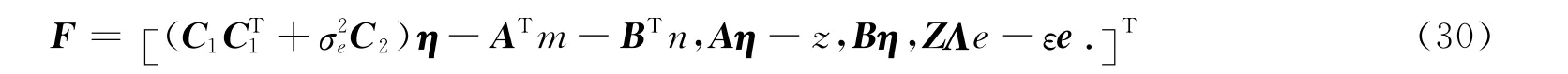
其中：Z＝diag（z1，…，z4N）；Λ＝diag（m1，…，m4N）；ε∈［0，1］；e＝［1，1，…，1］T.

约束最小化可通过迭代地更新矢量η来获得，该最小化包含在于寻找拉格朗日函数的平稳点.在最小化过程中，新的迭代值η是通过在此时估计值的基础之上增加一项Δη.利用约束高斯-牛顿法时，Δη应为等式

的解 .则第k+1次迭代更新值可取为

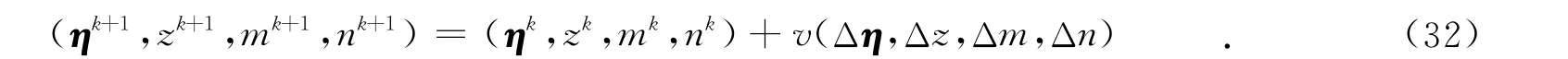
其中：搜索方向的步长应满足不等式（zk+1，mk+1）＞0成立，搜索方向由式（31）来求取.

5 结论

对于非线性系统的直接加权优化辨识算法，通过在原线性仿射函数形式中，增加若干项关于输入观测数据序列的线性项来增强逼近非线性，减少逼近的时间.对于增加若干线性项后展开式中的未知权重值的选取，分别从理论和实用上推导出这些未知权重值的选取过程.

理论上的推导分析，可明确增加的未知权重值在整个逼近非线性系统的目的中起着辅助作用；实用上的推导分析，则展示了如何将某些复杂的最优化问题经过整理变换成常见的最优化问题，从而可利用最为基础的优化方法来求解.

由于文中利用输入观测数据序列，而此输入观测数据需要人为事先选定以满足持续激励非线性系统，故对该非线性系统的选择持续激励的输入信号是目前需要深入研究的内容.

［1］ LJUNG L.System identification：Theory for the user［M］.New Jersey：Prentice Hall，1999.

［2］ BOYD S，VANDENBERGHE L.Convex optimization［M］.Cambridge：Cambridge University Press，2008.

［3］ ROLL J，NAZINY A，LIUNG L.Non-linear system identification via direct weight optimization［J］.Automatica，2005，41（3）：475-490.

［4］ ROLL J，BEMPORAD A，LIUNG L.Identification of piecewise affine systems via direct mixed integer programming［J］.Automatica，2004，40（1）：37-50.

［5］ ROLL J.Piecewise linear solution paths with application to direct weight optimization［J］.Automatica，2008，44（11）：2745-2753.

［6］ PAOLETTI S，ROLL J，GARULLI A，et al.On the input-output representation of piecewise affine state space models［J］.IEEE Transactions of Automatic Control，2010，55（1）：60-73.

［7］ BAI E W.Recursive direct weight optimization in nonlinear system identification：A minimal probability approach［J］.IEEE Transactions of Automatic Control，2007，52（7）：1218-1231.

［8］ PINTELON R，SCHOUKENS J.System identification：A frequency domain approach［M］.New York：IEEE Press，2001.

［9］ NOCEDAL J，WRIGHT S.Numerical optimization［M］.Berlin：Springer-Verlag，2002.

［10］ ZEILINGE M N，JONES CN，MORARI M.Real-time suboptimal model predictive control using a combination of explicit MPC and online optimization［J］.IEEE Transactions of Automatic Control，2011，56（7）：1524-1534.