发动机磁流变半主动悬置变论域模糊控制的研究

邓召学，郑 玲，李以农，张自伟

(重庆大学，机械传动国家重点实验室，重庆 400044)

前言

磁流变悬置是以磁流变液为载体构成的动力总成振动半主动控制装置，在磁场作用下，液体流变特性迅速改变［1］，从而使悬置阻尼力在较宽范围内可控。磁流变液悬置结构相对简单且便于实现，因此在发动机隔振中具有较高的研究价值［2］。

由于磁流变悬置本身的高度非线性和滞回特性［3］，建立合理的磁流变悬置正、逆模型是阻尼器用于振动控制的重要前提［4］。Bingham模型简单易于分析，能很好地表达阻尼器的力-位移特性，但不能描述磁流变阻尼器屈服前的特征［5－7］。文献［8］中提出了具有4参数的非线性滞回双黏模型，由实验发现该模型在低速区很难精确表示阻尼器的力学性能。神经网络［9］是最具应用前景的模型辨识方法之一。文献［10］中采用模糊自适应理论建立了磁流变阻尼器力学模型，该模型描述了阻尼器的滞回特性，但模型结构复杂，隶属度函数数目较多，易出现维数灾难。文献［11］中采用BP神经网络，以当前时刻和前一时刻的位移、速度、电流和前一时刻的阻尼力为输入及当前时刻的阻尼力为输出，建立了磁流变阻尼器的正向模型，但忽略了BP神经网络的权值和阈值选择的随机性对网络训练的影响，导致神经网络训练容易陷入局部极值。

目前，国内外学者对发动机磁流变悬置半主动控制也做了大量研究工作。文献［12］中对实时阻尼调节做了较深入的研究，实时阻尼可调方式的关键为确定输入信号(转速信号)与输出信号(磁流变悬置的励磁电流)之间精确的数学关系表达式，才能起到最佳的控制效果。文献［13］中以减小发动机对基座的垂向力为目标，设计了仿人思想修改参数的发动机垂直隔振模糊控制器。根据发动机激励频率和力传递率，通过建立的模糊规则可得到磁流变悬置需要的阻尼大小。文献［14］中为控制弹性梁结构振动，在结构中安装了混合模式的磁流变悬置，并设计了线性二次高斯(LQG)控制器，调节磁流变悬置的电流大小，从而得到最佳的控制力。

本文中以遗传算法(GA)优化BP神经网络的权值和阈值，利用遗传算法的全局搜索能力弥补了神经网络的局部极小化问题，通过磁流变悬置动态试验数据建立磁流变悬置GA-BPNN网络正、逆模型;最后通过编写变论域模糊控制S文件实现磁流变悬置系统的半主动控制。仿真结果表明:变论域模糊控制较传统模糊控制具有更好的宽频隔振效果，发动机转速对应的二阶主频位移和加速度振动峰值明显减小，验证了GA-BPNN网络模型及其变论域模糊控制算法的正确性和有效性。

1 磁流变悬置结构设计和动态性能试验

针对某动力总成设计了基于流动模式的磁流变液悬置结构，如图1所示。橡胶主簧上部通过加强块、连接螺栓与发动机连接，橡胶主簧与磁芯、磁芯与橡胶底膜之间分别形成上、下两个液室，液室中充满磁流变液体。上、下外磁芯和内磁芯之间构成环形阻尼通道，在外磁芯槽内缠绕励磁线圈。在发动机载荷作用下，橡胶主簧、加强块和连接螺栓一起上下运动，磁流变液通过阻尼通道在上下液室之间流动。当励磁电流改变时，环形阻尼通道内的磁感应强度也随之改变，阻尼通道中的磁流变液黏度发生改变，从而实现磁流变悬置输出阻尼力的无级、连续可调。

采用CRIMS电液伺服减振器性能试验机对自行设计的磁流变悬置进行动态性能试验。试验共采集了行程为0.5和1mm，频率范围为1～80Hz，频率间隔为5Hz，电流为0、0.25、0.5、0.75 和 1A 时的试验数据，为磁流变悬置模型的建立和控制算法的设计奠定基础。

2 GA-BP神经网络正、逆模型

神经网络具有高度的鲁棒性、自学习能力和非线性映射能力，为建立磁流变阻尼器的正、逆模型提供了一条有效的途径。前馈型BP神经网络拓扑结构见图2。图中，X1…Xn为BP神经网络的输入值，Y1…Ym为BP神经网络的预测值，ωij为输入层和隐含层之间的连接权值，ωjk为隐含层和输出层之间的连接权值，aj为隐含层阈值，bk为输出层阈值。但BP神经网络初始连接权值与阈值的随机选取，导致BP神经网络极易陷入局部极小值。因此，本文中提出以遗传算法(GA)优化BP神经网络的权值和阈值，用遗传算法的全局随机搜索能力弥补了神经网络的局部极小化问题，将优化后的GA-BPNN神经网络用于磁流变悬置的非线性正、逆模型的辨识，算法流程如图3所示。

GA-BP神经网络主要分为:BP神经网络结构确定、遗传算法优化和BP神经网络预测3部分。首先确定BP神经网络的初始结构，包括输入、输出参数的个数，隐含层节点数，进而确定遗传算法个体长度;然后用遗传算法对BP神经网络中的连接权值和阈值编码，确定适应度函数以得到误差较小的网络;最后采用选择、交叉和变异等遗传算子进行操作［15］，将遗传输出结果作为BP神经网络的初始权值和阈值，得到GA-BP预测模型，对GA-BP模型进行训练以达到要求精度。

2.1 GA-BP神经网络正模型

利用磁流变悬置动态性能试验数据，基于GABP神经网络对磁流变悬置正模型进行辨识，如图4所示。该网络有7个输入变量;前一时刻的位移Sk－1、电流 Ik－1、阻尼力 Fk－1与激振频率 fk－1和当前时刻的位移Sk、电流Ik与激振频率fk;网络输出变量为当前时刻的阻尼力Fk。

经过30代进化后，曲线收敛时对应的最小适应度值即阻尼力预测输出误差为10.35N，辨识结果具有较小的误差，如图5所示。图6为不同电流下，磁流变悬置阻尼力与激励频率关系的试验结果和GABP神经网络正模型预测结果，实线表示试验结果，虚线表示预测结果。从图中可以看出，辨识曲线与磁流变悬置性能试验数据趋势一致，表明GA-BP神经网络正模型预测结果具有较高的辨识精度。

2.2 GA-BP神经网络逆模型

基于GA-BP神经网络对磁流变悬置逆模型的辨识框图，如图7所示。该网络有7个输入变量:前一时刻的位移 Sk－1、电流 Ik－1、阻尼力 Fk－1与激振频率fk－1和当前时刻的位移Sk、阻尼力Fk与激振频率fk;网络输出变量为当前时刻的电流Ik。

经过30代进化后，曲线收敛时对应的最小适应度值即电流预测输出误差为0.011 3A，辨识结果具有较小的误差，如图8所示。图9为不同试验数据下，磁流变悬置激励电流的试验结果和GA-BP神经网络逆模型预测结果。辨识电流大小与磁流变悬置试验数据较好地吻合，表明GA-BP神经网络逆模型辨识精度高，满足控制系统设计的要求，为磁流变悬置半主动控制研究奠定了基础。

为评价GA-BP神经网络正、逆模型的逼近精度，建立如下指标［16］:

式中:Ex为阻尼力或电流相对逼近精度;xk为磁流变悬置的实际输出阻尼力或电流;x^k为神经网络辨识输出阻尼力或电流;n为离散点数。

表1为按式(1)算得的不同激励频率和不同电流下的相对逼近精度。由表可见:GA-BP神经网络正、逆模型的最低逼近精度为96.53%和97.94%，满足工程需要;表明GA-BP神经网络在磁流变悬置正、逆模型的辨识方面具有较高的辨识能力。

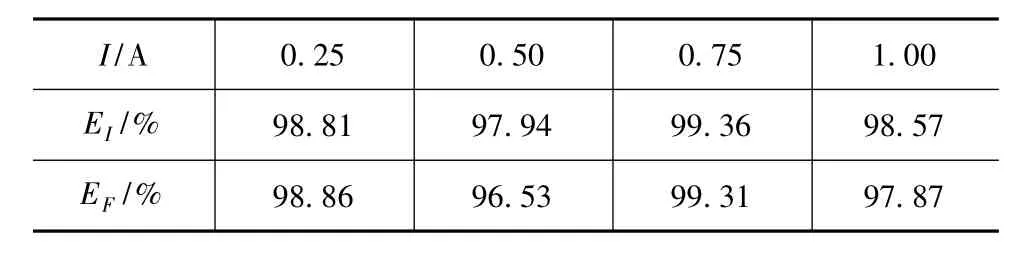
表1 GA-BP神经网络正、逆模型逼近精度

3 磁流变悬置变论域半主动控制

3.1 悬置系统动力学模型

图10为4缸四冲程直列式柴油发动机动力总成悬置系统的模型，它由3个磁流变悬置组成。

O0－XYZ为定坐标系，原点O0为发动机动力总成处于静平衡时的质心。X轴平行于曲轴，并指向汽车前方;Z轴垂直向上;Y轴依据右手定则确定。O－X'Y'Z'为动坐标系，当动坐标系处于静平衡时，动、定坐标系重合。同时，设系统的广义坐标为发动机动力总成沿X、Y、Z 3个方向的平动x、y、z和绕X、Y、Z 3 轴的转动 θx、θy、θz，即广义坐标 p 为

由拉格朗日方程推出发动机隔振的6自由度动力学方程［12］为

式中:Ms为质量矩阵;Cs为阻尼矩阵;Ks为刚度矩阵;F(t)为外激励矩阵;Bs为控制力输入矩阵;U为磁流变悬置可控力矩阵。发动机动力总成质量及其惯量参数如表2所示，发动机动力总成刚度、位置参数如表3所示。表3中ku、kv、kw分别表示悬置系统沿X、Y、Z轴的悬置刚度。

表2 发动机动力总成质量及其惯量参数

表3 发动机动力总成刚度、位置参数

3.2 变论域模糊控制系统设计

传统的模糊控制器输入、输出变量的论域一旦选定则在整个控制过程中都不能再修正，一旦论域选择偏大或偏小，都将严重影响模糊控制器的控制效果，并且控制器只具有相当于比例和微分的功能，无法在本质上消除系统静差，导致系统在微偏差范围内存在所谓的“控制死区”。

针对以上问题，本文中应用了变论域模糊控制算法［17－18］，变论域模糊控制能在控制过程中根据系统的输入和输出情况对初始论域进行动态调整，降低了对初始论域的要求;模糊控制器本质上就是插值控制器，采用变论域模糊控制器时，虽然规则形式不变，论域收缩使得规则局部细化，相当于增加了模糊规则数目，即插值点加密，从而提高了控制精度。

图11为双输入单输出变论域模糊控制器结构框图，输入论域随初始论域［－E，E］通过伸缩因子α变换为［－αE，αE］，输出论域随初始论域［－U，U］通过伸缩因子β变换为［－βU，βU］。α、β为误差变量的连续函数，本文中选用函数模型来表述［17］，设计输入和输出论域伸缩因子结构:

式中:ei∈［－E，E］，Δe∈［－U，U］，0 ＜λi＜1，i=1，2，0 ＜ γ ＜1。

图12为发动机磁流变悬置变论域模糊控制系统框图，发动机转速变化范围为650～3 000r/min。在变论域模糊控制器设计时，取各悬置点的垂向速度v和加速度a作为控制器的输入量，输出量为磁流变悬置理想控制力u，通过GA-BPNN神经网络磁流变悬置逆模型得到控制电流，再通过GA-BPNN神经网络磁流变悬置正模型得到实际的控制阻尼力。由于变论域模糊控制没有现成的Simulink框图，本文中通过编写S函数文件来实现。

取输入、输出量的模糊集合初始论域为［－6，6］。控制器的输入、输出语言变量均取7个模糊子集，分别为{NB，NM，NS，ZE，PS，PM，PB}，以经验和理论推导，建立“以最快的速度使发动机某点悬置的振动速度为零”标准的模糊控制规则，制定出求解悬置阻尼力的模糊控制规则，如表4所示。

表4 阻尼力的模糊控制规则

3.3 仿真试验

利用Matlab仿真软件，为YND485ZL 4缸四冲程的柴油发动机建立了基于被动液压悬置和磁流变液压悬置的发动机悬置系统仿真模型。仿真时，发动机采用单频率激励方式，对稳定转速为1 500r/min的磁流变悬置点1的垂向位移和加速度振动信号进行测量，对被动、模糊控制和变论域模糊控制3种策略进行对比，如图13～图16所示。

由图可见，发动机转速为1 500r/min时，在激振频率即发动机振动二阶主频50Hz位置处，相对被动悬置、模糊控制磁流变悬置的振动位移和加速度功率谱，变论域模糊控制振动位移和加速度功率谱幅值均有大幅下降。

从表5可知，发动机转速为1 500r/min时，模糊控制和变论域模糊控制位移均方根值相对于被动悬置分别降低了9.6%和24%;模糊控制和变论域模糊控制加速度均方根值相对于被动悬置分别降低了14.8%和30%。振幅下降非常显著，表明变论域模糊控制器设计是合理、有效的，很好地衰减了发动机工作时的振动幅值。

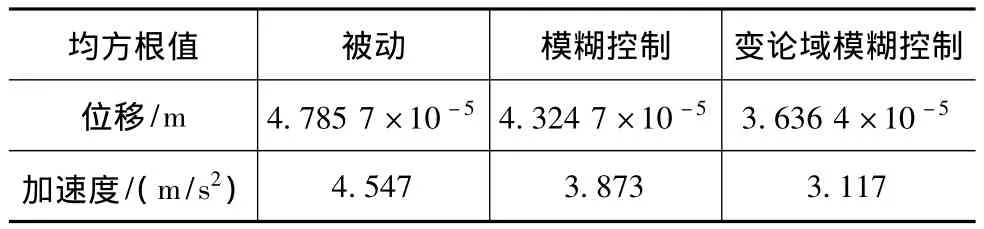
表5 悬置1点位移和加速度的均方根

4 结论

(1)由GA-BP神经网络正、逆模型训练迭代进化曲线和辨识精度结果可知，GA-BP神经网络的训练速度快，具有高度的辨识性能，适用于多批次、数据量大的磁流变悬置力学模型辨识，具有较好的应用前景。

(2)针对6自由度悬置系统，通过编写S函数文件，设计了变论域模糊控制策略;仿真分析结果表明，在模糊控制规则相同的情况下，变论域模糊控制的精度比传统的模糊控制精度高。

［1］ Koo J H，Goncalves F D，Ahmadian M．A Comprehensive Analysis of the Response Time of MR Dampers［J］．Smart Materials and Structures，2006，15(2):351 －358．

［2］ Carlson J D．Magnetorheological Fluid Actuators．Adaptronics and Smart Structures［M］．Edited by Jendritza DJ and Janocha H，Springer Verlag，1997．

［3］ Spencer Jr B F，Dyke S J．Phenomenological Model of a Magnetorheological Dampers［J］．ASCE Joumal of Engineering Mechanics，1997，123(3):230 －238．

［4］ Boada M J L，Calvo J A．Modeling of a Magnetorheological Damper by Recursive Lazy Learning［J］．International Journal of Non-Linear Mechanics 2011，46:479 －485．

［5］ Spencer B，Dyke S，Sain M，et al．Phenomenological Model for Magnetorheological Dampers［J］．Journal of Engineering Mechanics，1997，123(3):230 －238．

［6］ Gamato D，Filisko F E．High Frequency Dynamic Mechanical Study of an Aluminosilicate Electrorheological Material［J］．Journal of Rheology，1991，35:1411 －1425．

［7］ 周强，瞿伟廉．磁流变阻尼器的两种力学模型和试验［J］．地震工程与工程振动，2002，22(4):144 －150．

［8］ Wereley N，Pang L．Non-dimensional Analysis of Semi-active Electrorheological and Magnetorheological Dampers Using Approximate Parallel Plate Models［J］．Smart Materials and Structures，1998，7:732－743．

［9］ Du H，Lam J，Zhang N．Modeling of a Magneto-rheological Damper by Evolving Radial Basis Function Networks［J］．Engineering Applications of Artificial Intelligence，2006，19(8):869 －881．

［10］ Schurter K，Roschke P N．Fuzzy Modeling of a Magnetorheological Damper Using Anfis［C］．The Ninth IEEE International Conference Fuzzy Systems，2000．

［11］ 王修勇，宋璨．磁流变阻尼器的性能试验与神经网络建模［J］．振动与冲击，2009，28(4):42 －46．

［12］ 魏付俊．汽车动力总成磁流变悬置的设计和半主动控制研究［D］．南京:南京航空航天大学，2007．

［13］ 李锐．发动机磁流变悬置隔振模糊控制与仿真［J］．系统仿真学报，2009，21(4):944 －947．

［14］ Choi Seung-Bok，Hong Sung-Ryong，Sung Kum-Gil，et al．Optimal Control of Structural Vibrations Using a Mixed-mode Magnetorheological Fluid Mount［J］．International Journal of Mechanical Science，2008(50):559 －568．

［15］ 陈国良，王煦法．遗传算法及其应用［M］．北京:人民邮电出版社，2001．

［16］ 王昊，胡海岩．磁流变阻尼器的模糊逼近［J］．振动工程学报，2006，19(1):31 －36．

［17］ 李洪兴．变论域自适应模糊控制器［J］．中国科学E辑，1999，29(1):32－42．

［18］ 李良峰．变论域模糊控制算法研究［D］．成都:电子科技大学，2008．