高阶中立型偏微分系统的振动性分析
罗李平,罗振国,曾云辉
(衡阳师范学院 数学与计算科学系,湖南 衡阳 421002)
0 Introduction
The oscillation study of partial functional differential equations(PFDE)are of both theoretical and practical interest.Some applicable examples in such fields as population kinetics,chemistry reactors and control system can be found in the monograph of Wu[1].There have been some results on the oscillations of solutions of various types of partial functional differential equations.We mention here the literatures of Yu et al.[2],Liu and Fu[3],Wang and Yu[4],Wang and Feng[5],Luo et al.[6],Kiguradze et al.[7],Saker[8],Li and Debnath[9],Wang and Teo[10],Wang and Wu[11],Yang[12],Wang et al.[13]and the references cited therein.In addition,several authors including Li[14],Guan and Yang[15],Li and Cui[16],Li[17],Deng et al.[18],Li and Meng[19],Li et al.[20],Wang and Wu[21],Deng and Mu[22]have studied the oscillation problems of partial functional differential systems of different types.In spite of the above studies,hardly any attention was given to the problem of oscillation of high-order PFDE with continuous delay,especially the systems of high-order PFDE with continuous delay.However,we note that in many areas of their actual application,models describing these problems are often effected by such factors as seasonal changes.Therefore it is necessary,either theoretically or practically,to study a type of PFDE in a more general sense——PFDE with continuous delay.The main objective of this paper is to studythe oscillation of a class of systems of high-order neutral PFDE with continuous delay and nonlinear diffusion term.Some sufficient conditions are proved for the oscillation of such systems.It should be noted that in the proof we do not use the results of Dirichlet's eigenvalue problem.
1 Formulation of the Problem
In this paper,we study the oscillation of the following even order neutralpartial functional differential systems with continuous delay and nonlinear diffusion term

where n≥2is even,Ωis a bounded domain in Rmwith a piecewise smooth boundary∂Ω,Δis the Laplacian inRm,R+= (0,∞),the integral in(E)are Stieltjes ones.
Consider the Dirichlet's boundary condition:
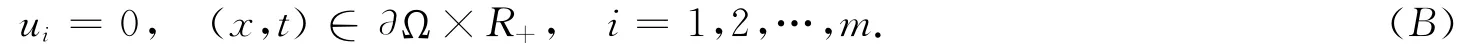
Throughout this paper,we assume that the following conditions hold:


(H7)τ(η),μ(ξ)is nondecreasing on[c,d]and[a,b],respectively.
Definition1.1A vector function u(x,t)= {u1(x,t),u2(x,t),…,um(x,t)}Tis said to be a solution of the boundary value problems(E),(B)if it satisfies(E)in Gand boundary condition(B)in∂Ω×R+.
Definition1.2A numeral function v(x,t)is said to be oscillatory in Gif for anyβ>0,there exists a point(x0,t0)∈ Ω× [β,∞)such that v(x0,t0)=0.A vector function u(x,t)of the boundary value problems(E),(B)is said to be oscillatory in Gif u(x,t)has at least one component as a numeral function to be oscillatory.We call a vector function u(x,t)of the boundary value problems(E),(B)to be nonoscillatory in Gif each component of u(x,t)is nonoscillatory.
The objective of this paper is to derive some newoscillatory criteria of solutions of the boundary value problems(E),(B).
To prove the main results of this paper,we need the following lemmas.
Lemma1.1(Kiguradze[23])Let y(t)∈Cn(I,R)be of constant sign,y(n)(t)≠0and y(n)(t)y(t)≤0on I,then
(ⅰ)there exists a t1≥t0,such that y(i)(t)(i=1,2,…,n-1)is of constant sign on[t1,∞);
(ⅱ)there exists an integer l∈ {0,1,2,…,n-1},with n+l odd,such that

Lemma1.2(Philos[24])Suppose that y(t)satisfies the conditions of Lemma 1.1,and y(n-1)(t)y(n)(t)≤0,t≥t1,then for everyθ∈ (0,1),there exists a constant N >0satisfying
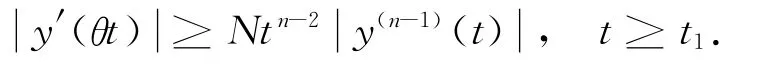
2 Main Results
Theorem2.1Suppose that there exists a functionρ(t)∈C1(I,R+),such that
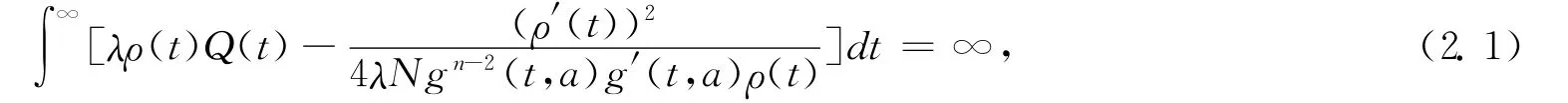
Whereλ=1-P ,the definitions of Pand Q(t)see(H1)and(H2),then all solutions of the boundary value problems(E),(B)are oscillatory in G.
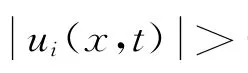
Integrating(E)with respect to xover the domainΩ,we have

It is easy to see that

Therefore,

TheGreen's formula,(B)and(D)yield

whereνis the unit exterior normal vector to∂Ω,dSis the surface element on∂Ω.
Combining(2.3)—(2.4),noting that(H2)and(H5),we have

Let Vi(t)=∫ΩZi(x,t)φ(x)dx ,t≥t1,i∈Im,it is obvious that Vi(t)>0,t≥t1,i∈Im.Then,from(2.5),we have

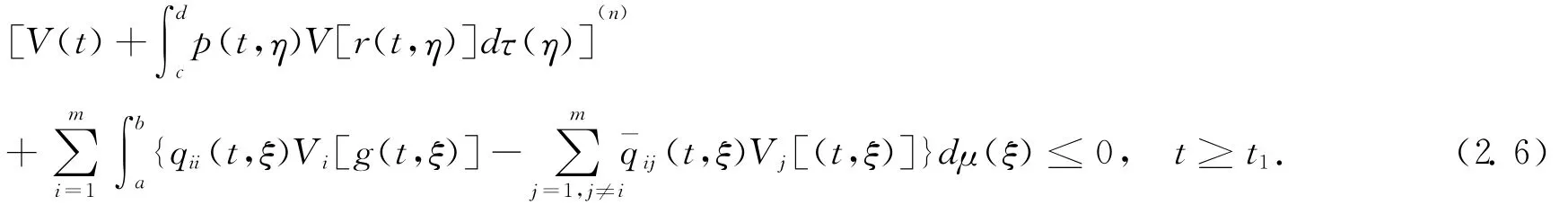
Noting that

Then,from (2.6),we have
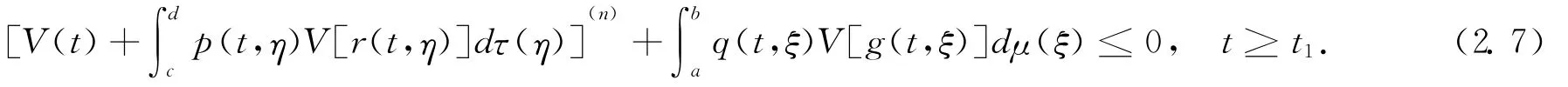
Setting

Noting that the assumption of p(t,η)and q(t,ξ),from (2.7)and(2.8),we have z(t)≥V(t)>0and

Thus,from Lemma 1.1,there exists a t2≥t1,such that

By choosing“l=1”and“l=n-1”,respectively,we have“z′(t)>0and z(n-1)(t)>0,t≥t2”.Form(2.8),we have

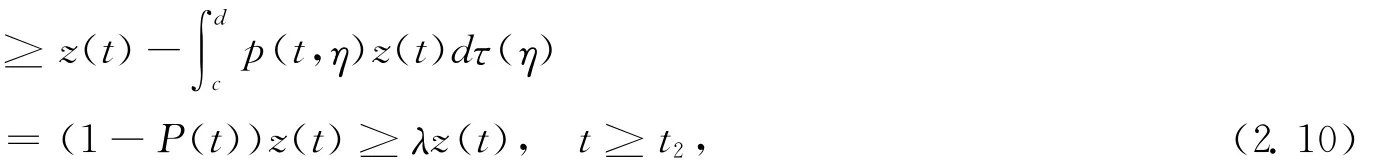
whereλ=1-P.
Combining(2.9)and(2.10)yields

where Q(t)is defined by(H2).
Letting

Then W(t)>0for t≥t2.Because z(t)is increasing,g(t,ξ)is nondecreasing with respect tot andξ,there exists a t3≥t2,such that


Thus,from (2.11)—(2.13),we have

Taking

From the fact that X2-2 XY+Y2≥0for any X,Y∈R,we obtain

Thus,form (2.14)—(2.15),we have

Integratingboth sides of(2.16)fromt4to t(t>t4),we have


The proof of Theorem 2.1is complete.
Hereinbelowwe consider the sets

Theorem2.2Assume that there exists functionρ(t),φ(t)∈C(I,R+),H(t,s)∈C(D,R),h(t,s)∈C(D0,R),such that
(ⅰ)H(t,t)=0,t≥t0,H(t,s)>0, (t,s)∈D0;
(ⅱ)H(t,s)φ(s)exists a continuous and nonpositive partial derivative on D0with respect to the variable s and satisfies the equality

If

for any T≥t0,whereλ=1-Pand

then all solutions of the boundary value problems(E),(B)are oscillatory in G.
Proof.Proceeding as in the proof of theorem 2.1,we have still(2.14)holds.Multiplying both sides of(2.14)by H(t,s)φ(s)for t≥T ≥t4,integrating fromTto t,we have

Therefore,

Taking

From the fact that X2-2 XY+Y2≥0for any X,Y∈R,we obtain

Combining(2.19)—(2.20),we get

The above formula yields

This contradicts(2.18).The proof of Theorem 2.2is complete.
Corollary2.3If condition(2.18)of Theorem 2.2is replaced by
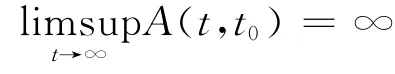
and

then the conclusions of Theorem 2.2remain true.
If the condition(2.18)don't hold,we have the following result.
Theorem2.4Assume that the other conditions of Theorem 2.2remain unchanged,the condition(2.18)of Theorem 2.2is replaced by

and

If there exists a functionψ(t)∈C(I,R)such that

and

whereψ+(s)= max{ψ(s),0},the definitions of A(t,T)and B(t,T)see(2.18),then all solutions of the boundary value problems(E),(B)are oscillatory in G.
Proof.Proceeding as in the proof of theorem 2.2,for any t≥T≥t4,we have still(2.21)holds,then

From(2.25)—(2.26),we have

and

From(2.24)and(2.27),we obtain
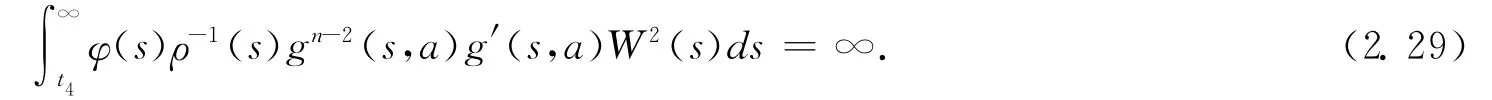
To complete the proof of this theorem,we merely need to prove that(2.29)is impossible.For this purpose,we definite

From(2.19)and(2.28),we have

From(2.22)and(2.29),we obtain


From(2.31),we have

Combining(2.32)and(2.33),we get

and
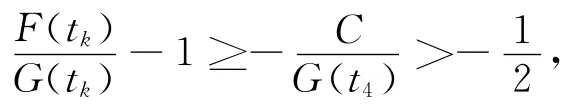
namely,

Fromthe above formula and(2.34),we have

On the other hand,by using the Schwarz's inequality,we obtain

Thus,we have

Noting that(2.35),we obtain

[1]Wu J H.Theory and applications of partial functional differential equations[M].New York:Springer-Verlag,1996.
[2]Yu Y H,Liu B,Liu Z R.Oscillation of solutions of nonlinear partial differential equations of neutral type[J].Acta Math.Sini.,1997,13(4):563-570.
[3]Liu X Z,Fu X L.Oscillation criteria for high order delay partial differential equations[J].J.Appl.Math.Stochastic A-nal.,1998,11(2):193-208.
[4]Wang P G,Yu Y H.Oscillation criteria for a nonlinear hyperbolic equations boundary value problem [J].Appl.Math.Lett.,1999,12(1):91-98.
[5]Wang P G,Feng C H.Oscillation of solutions for parabolic equation[J].Comput.Appl.Math.,2000,126(2):111-120.
[6]Luo J W,Liu Z R,Yu Y H.Oscillation theorems for hyperbolic equations of neutral type[J].Bull.Inst.Math.Acad.Sinica,2001,29(1):135-145.
[7]Kiguradze I T,Kusano T,Yoshida N.Oscillation criteria for a class of partial functional-differential equations of higher order[J].J.Appl.Math.Stochastic Anal.,2002,15(3):255-267.
[8]Saker S H.Oscillation criteria of hyperbolic equations with deviating arguments[J].Publ.Math.Debrecen,2003,62(1):165-185.
[9]Li W N,Debnath L.Oscillation of higher order neutral partial functional differential equations[J].Appl.Math.Lett.,2003,16:525-530.
[10]Wang P G,Teo K L.Oscillation of solutions of parabolic differential equations of neutral type[J].J.Math.Anal.Appl.,2005,311(2):616-625.
[11]Wang P G,Y.H.Wu Y H.Forced oscillation of a class of neutral hyperbolic differential equations[J].J.Comput.Appl.Math.,2005,177(2):301-308.
[12]Yang Q G.On the oscillation of certain nonlinear neutral partial differential equations[J].Appl.Math.Lett.,2007,20:900-907.
[13]Wang P G,Wu Y H,Caccetta L.Oscillation criteria for boundary value problems of high-order partial functional differential equations[J].J.Comput.Appl.Math.,2007,206(1):567-577.
[14]Li Y K.Oscillations of systems of hyperbolic differential equations with deviating arguments[J].Acta Math.Sinica 1997,40(1):100-105.
[15]Guan X P,Yang J.Oscillation of systems of nonlinear hyperbolic partial functional differential equations of neutral type[J].J.Sys.Sci.&Math.Scis.,1998,18(2):239-246.
[16]Li W N,Cui B T.Oscillation for systems of neutral delay hyperbolic differential equations[J].Indian J.Pure Appl.Math.,2000,31:933-948.
[17]Li W N.Oscillation properties for systems of hyperbolic differential equationsof neutral type[J].J.Math.Anal.Appl.,2000,248:369-384.
[18]Deng L H,Ge W G,Yu Y H.Oscillation of systems of quasilinear parabolic functional differential equations about boundary value problems[J].Acta Math.Appl.Sinica,2001,24(2):295-301.
[19]Li W N,Meng F W.Oscillation for systems of neutral partial differential equations with continuous distributed deviating arguments[J].Demonstratio Math.,2001,34:619-633.
[20]Li W N,Cui B T,Debnath L.Oscillation of systems of certain neutral delay parabolic differential equations[J].J.Appl.Math.Stochastic Anal.,2003,16(1):83-94.
[21]Wang P G,Wu Y H.Oscillation of solutions for systems of hyperbolic equations of neutral type[J].Electronic of Differential Equations,2004,2004(80):1-8.
[22]Deng L H,Mu C L.Oscillation of solutions of the systems of quasilinear hyperbolic equations under nonlinear boundary condition[J].Acta.Math.Scientia,2007,27B(3):656-662.

[24]Philos Ch G.A new criterion for oscillatory and asymptofic behavior of delay differential equations[J].Bull.Acad.Pol.Sci.Ser.Sci.Mat.,1981,29:367-370.
——庆祝湖南农业大学草业科学系建系20 周年

