基于多量子比特Greenberger－Horne－Zeilinger纠缠态的受控远程量子信息凝聚

陈银花，张登玉，汪新文，谢利军

（衡阳师范学院 物理与电子信息科学系，湖南 衡阳 421002）

0 Introduction

An unknown quantum state cannot be perfectly copied is a consequence of linearity of quantum theory.It has been shown by Bužek and Hillery［1］that it is possible to clone an unknown pure state of a single input qubit into two output qubits with a certain fidelity smaller than one.Although the fidelities of clones relative to the original state are less than one，the quantum information of the input system is not degraded but only distributed into a larger quantum system.That is，the quantum cloning process can be regarded as the distribution of quantum information from an initial system to final ones.Thus，quantum cloning combined with other quantum information processing tasks may have potential applications in multiparty quantum communication and distributed quantum computation.This leads to the advent of the concept of quantum telecloning［2］，which is the combination of quantum cloning and quantum teleportation［3］.Indeed，it can be seen as a process of distributing quantum information of a qubit from a sender to many distant receivers without violation of the quantum no－cloning theorem.Later，remote information concentration，the inverse of telecloning has been presented by Murao and Vedral［4］.They considered that the quantum information of a single qubit was previously distributed to three spatially separated qubits by the asymmetric telecloning procedure，can be remotely concentrated back to a single qubit by a four－qubit unlockable bound entangled state［4］based on Bell－state measurement and an appropriate unitary operation.Telecloning and concentrating process could be regarded as，respectively，remote information depositing and withdrawing，or remote information encoding and decoding，which are expected to find useful applications in network－based quantum information processing［4］.So a number of works were focused on remote information concentration due to its potential applications in quantum information science.Yu et al.［5］showed that a four－qubit GHZ state can be used to implement three－to－one remote information concentration.Later，a scheme for remote information concentration of three two－level atoms in cavity QED was proposed，which did not need Bell－state measurement［6］.Recently，remote information concentration was generalized to the N→1case in two－level systems［7－8］.Not long ago，it was shown that remote information concentration could be achieved probabilistically with a four－qubit cluster state［9］state as the quantum channel.Remote information concentration in d－level systems was also studied［10］.

In this Letter，we will give an efficient scheme of remote information concentration via a five－qubit GHZ state following idea of in quantum state sharing［11－13］.It will be shown that the quantum information of a single qubit which has been originally distributed into three spatially separated qubits can be remotely concentrated back to a single qubit in a control manner.The feature of the scheme is that the success of remote information concentration depends on the permission of the controller.Without the cooperation of the controller，the receiver cannot reconstruct the original state.We also generalize this scheme to the case with nspatially－separated controllers via an （n ＋ 4）－qubit GHZ state as the quantum channel.We expect our work combined with quantum cloning will be useful in quantum cryptography［14］and quantum key distribution［15］as the modern technology allows the quantum key distribution to be implemented in the laboratory and allows application for quantum cryptography in the future.

1 Controlled remote information concentration

Remote information concentration begins with a situationthat the information of an unknown state｜x〉＝α｜0〉＋β｜1〉（｜α｜2＋｜β｜2＝1）is diluted to a composite system consisting of qubits A，B，and C，which was hold by three separate parties，i.e.，Alice，Bob，and Charlie，respectively.Assume that the three qubits are in a cloning state｜ψ〉ABCafter the asymmetric telecloning procedure

whereαandβare complex numbers satisfying｜α｜2＋｜β｜2＝1.The states｜φ0〉ABCand｜φ1〉ABCare defined as

whereq＋p＝1，q≥p，Nis a normalization factor given by N＝1＋p2＋q2.Our goal is concentrating the information initially distributed in three spatially separated qubits A ，Band Cto a single remote qubit without performing any global operations.

For simplicity，let us first consider a way for the remote information concentration of one controller with a five－qubit GHZ state as the quantum channel：

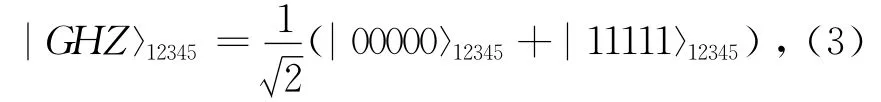
where the qubits 1，2，3，4and 5belong to Alice，Bob，Charlie，David，and Eve respectively.The whole system ｜Θ〉ABC12345＝ ｜ψ〉ABC｜GHZ〉12345is given by

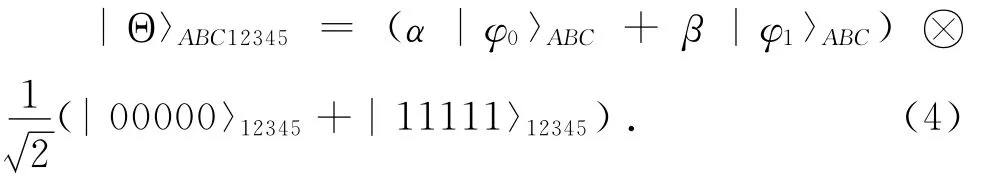
Same as in Ref.［5］，the three parties Alice，Bob，and Charlie perform Bell－state measurements on their respective pairs of qubits Aand 1，Band 2，Cand 3.They are randomly in one of the four Bell states

As an example for demonstrating the principle of this remote information concentration scheme，we assume that the outcomes obtained byAlice，Bob and Charlie are ｜Φ＋〉A1，｜Φ＋〉B2，and｜Φ＋〉C3respectively.Then the retained two qubits are in the state

The no－cloning theorem allows only one qubit to be in the original state｜x〉＝α｜0〉＋β｜1〉，so that any one of David and Eve，but not all，can recover such a state.In order to recover the original state，David and Eve need to cooperate.We assume that David agree to help Eve to reconstruct the original state，he performs the single－qubit measurement on his qubit 4in the basis｛｜＋〉，｜－〉｝，which are given by

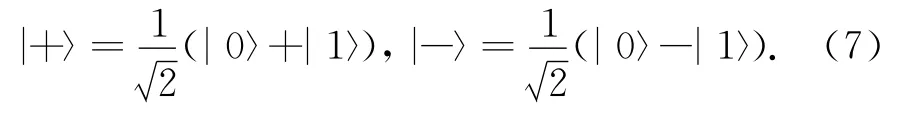
Then the state｜φ〉45can be written as

That is，Eve can recover the original state｜x〉＝α｜0〉＋β｜1〉with a unitary operation if he knows the single－qubit measurement outcome done by David.For example，when the outcome of David is｜＋〉4，Eve should perform the unitary operation U0on the qubit 5to recover the original state.The unitary operations Um（m ＝0，1，2，3）are given by

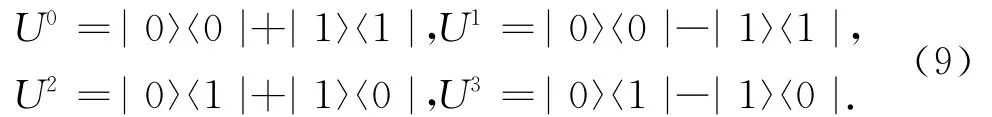
For the other case，the relation between the measurement results and the unitary operations needed to recover the original state｜x〉＝α｜0〉＋β｜1〉is shown in table1.Similar to Refs.［11－13］，we define Vas the bit value of the result of the Bell state，i.e.，V｜Φ±〉≡0，V｜ψ±〉≡1.That is，the bit value V＝0if the states of the two qubits are parallel，otherwise V＝1.Vtotal＝VA1⊕VB2⊕VC3.Pdenotes the parity of the result of the Bell－state measurement and the single－qubit measurement in the basis｛｜＋〉，｜－〉｝，i.e.，P｜Φ±〉 ≡± ，P｜ψ±〉≡±，P｜±〉≡±.Ptotal＝PA1⊗PB2⊗PC3.

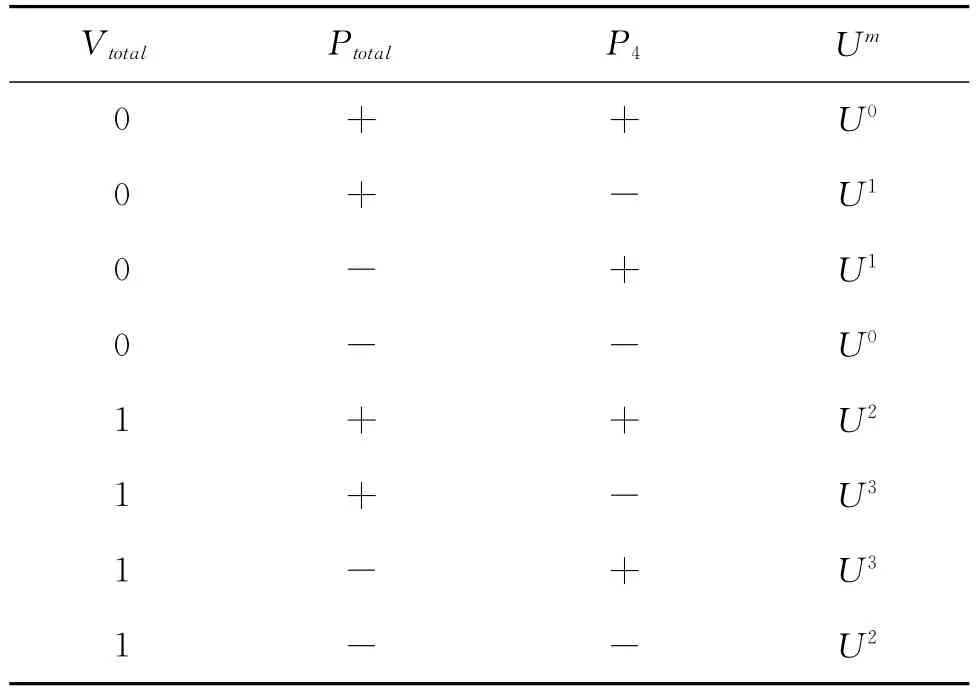
Table1.The relations between the measurement results and the unitary operations.Umis the unitary operation done by Eve on qubit 5to reconstruct the original state.

It is straightforward to generalize this scheme to the case with nspatially－separated controllers.Similar to Refs.＼［11－13］，for this multiparty remote information concentration scheme，Alice，Bob，Charlie，Davidi（i ＝ 4，5，…，n ＋3），and Eve share an（n＋4）－qubit GHZ state given by

Then the composite state of the system is

AfterAlice，Bob and Charlie takes the Bellstate measurements on the qubits Aand 1，Band 2，Cand 3，respectively，the state of the subsystem（without being normalized）becomes

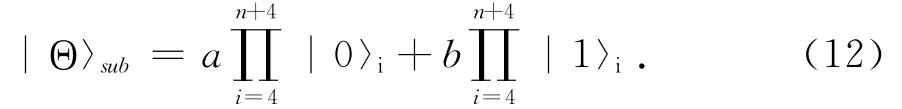
Therelations between the parameters a，band the results Vtotaland Ptotalare shown in table 2.

Table2.The relation between the values of a，band the results Vtotaland Ptotal.

When the spatially－separated controllers Davidi（i＝4，5，…，n＋3）want to help the receiver Eve to reconstruct the original state｜x〉＝α｜0〉＋β｜1〉，the nspatially－separated controllers perform the single－qubit measurements on their qubits in the basis｛｜＋〉，｜－〉｝independently.The measurements done by them can be expressed by the formula Mas follows

Heretis the number of the controllers who obtain the result｜－〉.After the measurements done by Alice，Bob，Charlie and the ncontrollers，the final state｜φ〉n＋4can be gained by means of performing the operation Mon the state｜Θ〉sub，

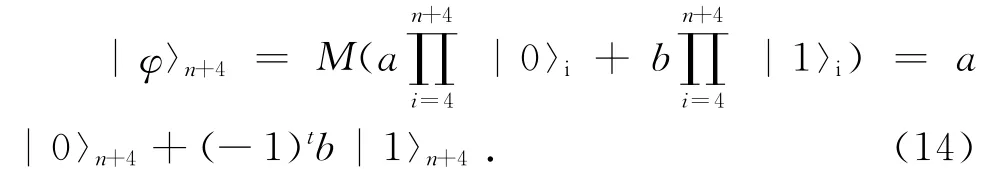
We define

WherePiis the result of the single－qubit measurement done by the i－th controllers.The relations between the results of the measurements and the unitary operations with which Eve can reconstruct the original state are the same as in table 2 just with a little modification.That is P4is replaced byPc.

2 Discussion and conclusion

Insummary，we have studied the remote information concentration scheme in a control manner.That is，the information of the three－qubit cloning state can be remotely and deterministically concen－trated back to a single qubit with the help of the controller via the five－qubit GHZ state.We have also generalized the scheme to the case with nspatially－separated controllers via an （n ＋ 4）－qubit GHZ state.In the scheme，the GHZ state serves as not only the control parameter but also the quantum channel.Moreover，telecloning and concentrating process could be regarded as remote information depositing and withdrawing，respectively，or remote information encoding and decoding，which are expected to find useful applications in network－based quantum information processing［4］.So our work will be useful in quantum information science such as quantum cryptography［14－15］.Especially，experimental realization of muti－photon GHZ state has been reported［16－18］.We hope our work will be realized in experiment in near future.

［1］Buzek V，Hillery M.Quantum copying：beyond the nocloning theorem ［J］.Phys.Rev.A，1996，54：1844－1852.

［2］Murao M，Jonathan D，Plenio M.B，et al.Quantum telecloning and multiparticle entanglement［J］.Phys.Rev.A，1999，59：156－161.

［3］Bennett C H，Brassard G，Crepeau C，et al.Teleporting an unknown quantum state via dual classical and Einstein－Podolsky－Rosen channels［J］.Phys.Rev.Lett.，1993，70（13）：1895－1899.

［4］Murao M，Vedral V.Remote information concentration using a bound entanled state［J］.Phys.Rev.Lett.，2001，86（2）：352－355.

［5］Yu Y F，Feng J，Zhan M S.Remote informtaiton concentration by a Greenberger－Horne－Zeilinger state and by a bound entangled state［J］.Phys.Rev.A，2003，68（2）：024303－024307.

［6］Wu Z Z，Fang M F.Remote three－atom information concentration without Bell－state measurement ［J］.Chin.Phys.Lett.，2006，23：1683－1686.

［7］Hsu L Y.Remote one－qubit information concentration and decoding of operator quantum error－correction codes［J］.Phys.Rev.A，2007，76（3）：032311－032314.

［8］Augusiak R，Horodecki P.Generalized Smolin states and their properties［J］.Phys.Rev.A，2006，73：012318－012327.

［9］Chen Y H，Zhang D Y，Gao F，et al.Remote information concentration via a four－particle cluster state ［J］.Chin.Phys.Lett.，2009，26：090304－090307.

［10］Wang X W，Zhang D Y，Yang G J，et al.Remote information concentration and multipartite entanglement in multilevel systems［J］.Phys.Rev.A，2011，84：042310－042317.

［11］Yang C P，Chu S I，Han S.Efficient many－party controlled teleportation of multiqubit quantum information via entanglement ［J］.Phys.Rev.A，2004，70：022329－022338.

［12］Deng F G，Li C Y，Li Y S，et al.Symmetric multiparty－controlled teleportation of an arbitrary two－particle entanglement ［J］.Phys.Rev.A， 2005， 72：022338－022346.

［13］Aldana S，Wang Y D，Bruder C.Greenberger－Horne－Zeilinger generation protocol for N superconductiong transmon qubits capacitively coupled to a quantum bus［J］.Phys.Rev.B，2011，84：134519－134527.

［14］Ekert A.Quantum cryptography based on Bell's theorem［J］.Phys.Rev.Lett.，1991，67：661－663.

［15］Karlsson A，Koashi M，Imoto N.Quantum entanglement for secret sharing and secret splitting［J］.Phys.Rev.A，1999，59：162－168.

［16］Zheng S B.One－step synthesis of multiatom Greenberger－Horne－Zeilinger states［J］. Phys.Rev.Lett.，2001，87：230404－230407.

［17］Wu C，Chen J L，Kwek L C，et al.Quantum nonlocality of N－qubit W states［J］.Phys.Rev.A，2006，73：012310－012314.

［18］Mikami H，Li Y，Fukuoka K，et al.New high－efficiency source of a three－photon W state and its full characterization using quantum state tomography［J］.Phys.Rev.Lett.，2005，95：150404－150407.