基于相对贴近度的不确定多属性决策法及其在人才引进中的应用

屈文阁

(陕西理工学院人事处，陕西汉中723000)

由于客观事物的复杂性和不确定性，以及决策者的积极参与，对方案有偏好信息的不确定多属性决策问题已成为现代决策科学中的一个研究热点[1-9］。目前，一些学者对此进行了研究并提出了一些方法。如文献[1-2］研究了属性权重未知、属性值和偏好信息均以区间数效用值形式给出的不确定多属性决策问题，分别提出了最小偏差法与线性规划法;文献[3-4］研究权重信息部分确知、偏好信息分别为区间数互反和互补矩阵判断的不确定多属性决策问题。分别提出了基于区间数正理想点及其投影的方案排序法[3］和基于C-OWA算子的决策方法[4］。文献[5］针对属性值以区间数形式给出并且已知方案偏好信息的多属性决策问题，提出了一种灰色关联分析的决策方法。文献[6］研究了方案偏好信息以区间数互反判断矩阵形式给出，属性偏好信息以区间数互补判断矩阵形式给出的不确定多属性决策问题。基于区间判断矩阵的一致性建立目标规划模型获得权重，并将区间属性值数值化进行排序，存在信息损失。文献[7］研究了权重信息为区间数、属性值为直觉模糊数且决策者对方案的偏好信息以直觉判断矩阵形式给出的模糊多属性决策问题。提出了基于线性规划和得分矩阵的决策方法。文献[8－9］基于直觉模糊集理论研究了对方案有偏好的不确定多属性决策问题，利用区间直觉模糊有序加权算术与几何平均算子对信息进行集结，利用得分函数和精确函数对方案进行排序。本研究在上述文献的基础上，针对权重信息部分确知且对方案有偏好的不确定多属性决策问题。基于主观偏好信息，建立一个目标规划模型，通过求解该模型得到属性权重，进而获得加权规范化矩阵。对TOPSIS法进行改进，并利用相对贴近度方案进行排序或择优。最后，将方法应用于人才引进问题验证了方法的可行性和有效性。

1 问题描述及决策矩阵的规范化

权重信息部分确知且对方案有偏好信息的不确定多属性决策问题的基本模型可以描述为:设X={x1，x2，…，xn}为方案集，S={s1，s2，…，sm}为属性集，ω =(ω1，ω2，…，ωm)T为权重向量，并设 Φ ={ω =(ω1，ω2，…，ωm)T，ω∈为已知的部分权重信息所确定的可能权重集合。记 M={1，2，…，m}，N={1，2，…，n}，则 i∈M，j∈N。决策者对方案 xj∈x的主观偏好信息为对于方案xj，按第i个属性si进行测量得到xj关于si的属性值为区间数从而构成属性决策矩阵，最常见的属性类型一般分为效益型和成本型。效益型是指越大越好的属性;成本型是指越小越好的属性。设I1、I2分别表示效益型、成本型下标集合，易知M=I1∪I2。

一般而言，不同的评价属性往往具有不同的物理量纲和量纲单位，为了消除不同量纲和量纲单位带来的不可公度性，决策之前应将属性进行无量纲和规范化处理。为此，根据评价属性的类型，按公式(1)、(2)把属性决策矩阵转为规范化[1］矩阵，其中，且

2 决策方法

定义[1］1 设区间数，称为区间数与的距离。

由于属性权重不完全确知，我们需先确定属性权重以便对方案排序。考虑决策信息与决策者的偏好一致化，且各决策方案之间是公平竞争的。为此，建立下列目标规划模型:

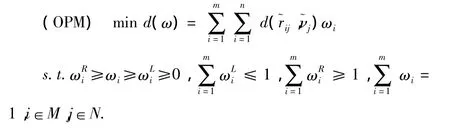
利用LINGO软件求解上述模型获得属性权重ω并代入(3)式，即可得到加权属性矩阵

为了对方案进行排序，首先，给出下列定义:

定义[4］2 如果记，且

其次，计算第j方案与正理想解和负理想解的投影:

最后，计算各方案的相对贴近度:

由于理想解和负理想解事实上不一定存在。易知，方案的优劣的排序即为λj由大到小的排序。

基于上述讨论，下面通过某高校人才引进的决策问题，给出求解步骤并说明模型及排序方法的有效性。

3 算例

高校人才引进是一个多因素的决策问题，决策者一方面要把德才优秀的人才引进，另一方面，也希望在条件相当的情况下引进自己所偏爱的人才。假设某高校制定的考核主要指标(属性)为:人力成本(s1);知识结构和创新能力(s2);思想品德(s3);后期培养费(s4)。显然，s2与s3为效益性属性，s1与s4为成本型属性。现有4名候选人xj(j=1，2，3，4)，决策者对每位候选人各指标进行打分，经过数据处理候，选人的属性值及属性权重信息列于表1:

表1 原始决策矩阵和权重信息Tab.1 Original decision-making matrices and weighting information

Setp1利用公式(1)、(2)，由表1可得到规范化决策矩阵如下:

Step2利用模型(OPM)，求解得属性权重向量为:ω=(0.32，0.15，0.35，0.18)T，从而由(3)式可得加权的规范化决策矩阵:

Step3由(4)、(5)式确定理想解和负理想解为:

由(6)、(7)、(8)式可计算解得相对贴进度为:λ1=0.531 7;λ2=0.037 4;λ3=0.276 5;λ4=0.912 2。从而 4位候选人的优先为x4＞x1＞x3＞x2，故首先考虑引进x4作为最佳选择。

4 结束语

本研究针对权重信息部分确知且对方案有主观偏好信息的不确定多属性决策问题，提出一种基于目标规划和相对贴进度的决策方法并应用于人才评价中。该方法不仅能充分利用主客观信息，最大限度地体现决策者的主观愿望，使得决策结果更具合理性。而且算例表明该方法具有计算简单易于上机实现的优点，从而为求解不确定性的多属性决策问题提供了一条新途径。

[1]徐泽水.不确定多属性决策方法及应用[M］.北京:清华大学出版社，2004.

[2]姜艳萍，樊治平.给出方案偏好信息的区间数多指标决策方法[J］.系统工程与电子技术，2005，27(2):250—252.

[3]Xu ZS.On method for uncertain multiple attribute decision making problems with uncertain multi-plicative preference information on alternatives[J］.Fuzzy Optimization and Decision Making，2005，4(2):131—139.

[4]Zhou HA，Liu SY，Fang XR.Method for uncertain multi-attribute decision making with preference information in the form of interval numbers complementary judgment matrix[J］.Journal of Systems Engineering and Electronics，2007，18(2):265—269.

[5]卫贵武，魏宇.对方案有偏好的区间数多属性灰色关联决策模型[J］.中国管理科学，2008，16(1):255—261.

[6]冯向前，魏翠萍，钱晓华.基于偏好信息一致性程度最大的多属性决策方法[J］.运筹与管理，2012，19(4):73—77.

[7]徐泽水.直觉模糊偏好信息下的多属性决策途径[J］.系统工程理论与实践，2007，27(11):62—71.

[8]卫贵武.对方案有偏好的区间直觉模糊多属性决策方法[J］.系统工程与电子技术，2009，31(1):116—120.

[9]夏梅梅，魏翠萍.对方案有偏好的直觉模糊多属性决策方法[J］.计算机工程与应用，2009，45(2):137—139.