移动机器人模糊滑模轨迹跟踪控制

张显伟， 吴忠伟， 张凤海， 刘克平＊

（1.中水东北勘测设计研究有限责任公司 机电设计处，吉林 长春 130021；2.长春工业大学 电气与电子工程学院，吉林 长春 130012）

0 引 言

近年来，移动机器人在工业、服务业、国防等很多领域发挥着重要的作用，由于移动机器人可以通过移动来完成一些如深海探测、地雷探测、无人机驾驶等危险的任务而受到广泛的关注［1－2］。

移动机器人有很多种，最常见的是在地面上依靠轮子移动的机器人，也被称为“无人驾驶车”或“移动小车”。移动机器人是一种受非完整约束的控制系统，对其控制及规划等问题显得较为复杂，因而一直被国内外很多专家学者所重视。由于在实际系统中难免会存在一些难以确定的外界干扰等因素的影响，使得一些基于确定模型设计的控制律不能达到理想的预期效果。因此，很多专家提出多种方法用来解决移动机器人的轨迹跟踪问题。Gu D［3］等用神经预测方法实现对机器人的轨迹跟踪，陈少斌［4］等设计了一种最优反馈状态跟踪器来达到跟踪参考轨迹的目的。U Kunar［5］等采用Backstepping反演控制的方法设计了轨迹跟踪控制律，很好地完成了轨迹的跟踪控制。

滑模控制是一种不需要获得被控对象精确的数学模型的非线性控制方法［5－6］，只需要知道模型中参数的变化范围。且其对一类有界的干扰和参数变化等影响具有不敏感性，这样在一定程度上大大地削弱了由于负载的变化或随机干扰给控制系统带来的影响。因此，滑模控制在轨迹跟踪控制方面得到了很大发展，也有很好的应用前景。然而，常规的滑模变结构控制的滑动模态是在逻辑切换能瞬时实现的条件下存在的，如果切换开关的选取不理想，就会产生高频抖振，使系统很难维持长时间的正常工作。模糊控制是一种适用于系统模型不能精确描述或者参数有变化的控制对象的智能控制方法，其基本思想是利用计算机来实现用模糊语言表达的反映专家经验和知识的控制规则。该方法是一种典型的计算机控制方法，与神经网络、预测控制等其它智能控制结合后，在实际应用中有很大的发展潜力。

文中结合模糊控制对系统模型的不完全依赖性和滑模控制的强鲁棒性提出了模糊滑模控制方案。基于模糊滑动面的定义给出模糊控制规则，通过适当的模糊逻辑推理给出模糊控制器的输出，设计一维的模糊控制器，根据S绝对值的大小来对趋近律参数进行调整，实现提高到达段运动品质的目的。保证了模糊控制系统的稳定性，有效地削弱了滑模控制中的抖振现象。

1 移动机器人运动学模型建立

文中研究对象是轮式移动机器人，该机器人由两个较大的后轮和两个较小的前轮组成，分别为驱动轮和从动轮。左右两个后轮分别各有一个电机来驱动小车的运动，若两个电机的转速不同，那么左右两个后轮会产生“差动”，即可实现移动小车的转弯动作［10－11］。该轮式移动机器人的位姿误差坐标图如图1所示。

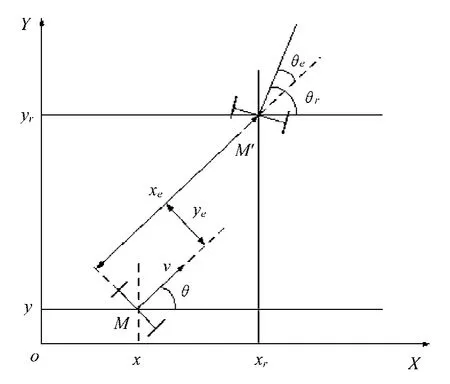
图1 移动机器人位姿误差坐标图

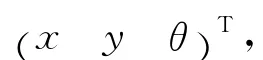
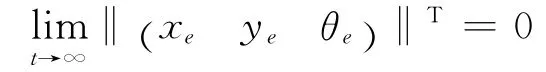
移动机器人的运动学方程为

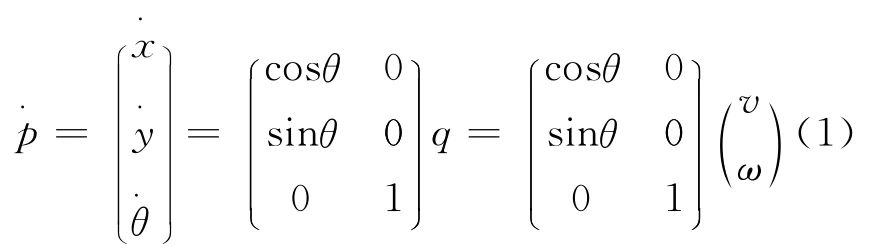
即

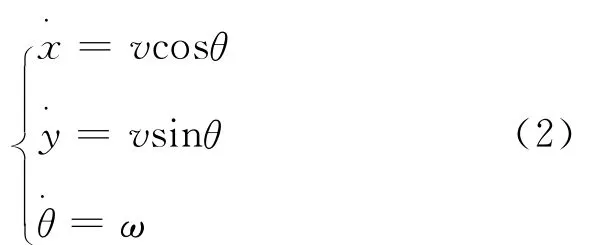
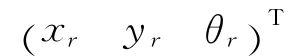
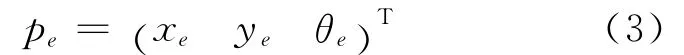
其中，θe＝θr－θ。设新坐标系Xe－Ye与坐标系X－Y之间的夹角即为θ。利用坐标变换得到：

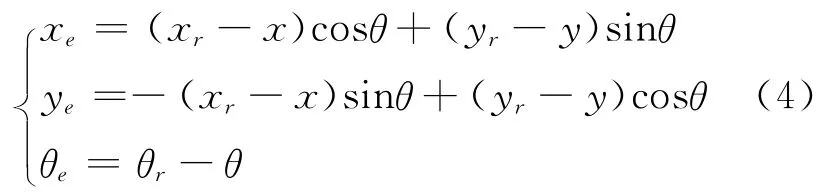
整理，得

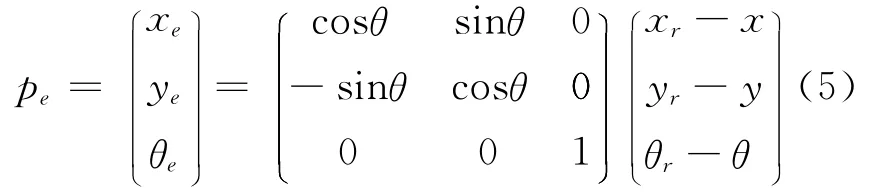
由式（2）可得

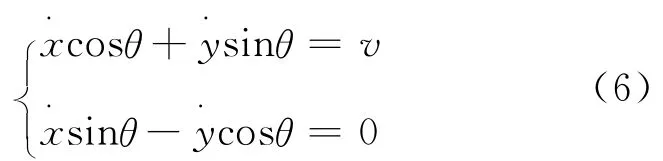
对式（4）各项求微分，得出关于机器人位姿误差的微分方程为

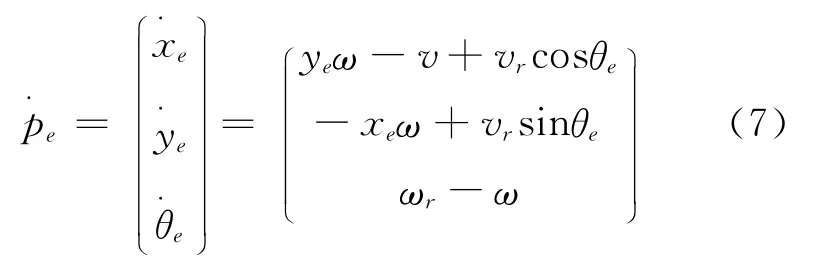
2 模糊滑模控制器的设计

2.1 基于反演（Backstepping）控制律的滑模切换函数设计

根据运动学方程和Backstepping的控制思想［8］构造滑模控制的切换函数。其设计思想是：

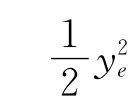
假设

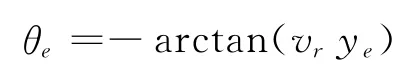
则

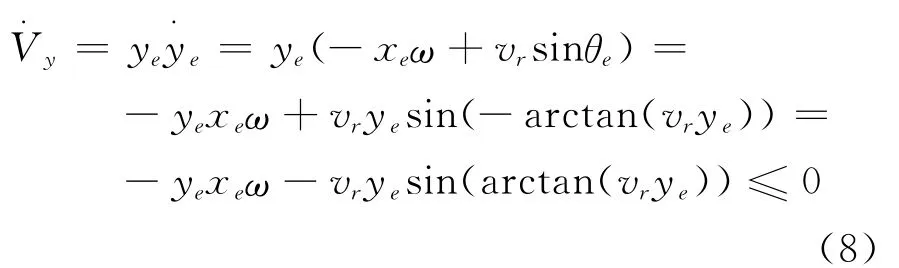
由此可知，θe＝－arctan（vrye）时可使ye收敛。因此，只要保证xe能够收敛到零，θe能够收敛到－arctan（vrye），那么ye也就能收敛到零。所以，只要设计出合适的控制输入v和ω，使xe→0，θe→－arctan（vrye），系统的状态都将是收敛的。根据这个思想，切换函数设计为：

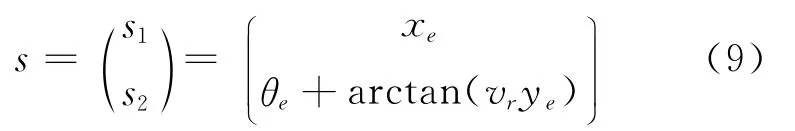
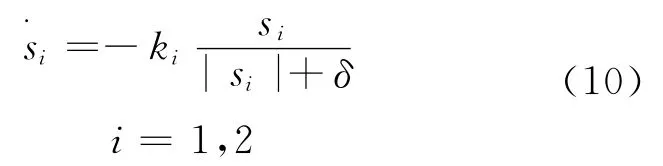
令α＝arctan（vrye），由式（7）和式（9），得

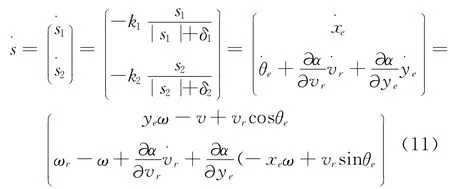
经整理，得控制律为

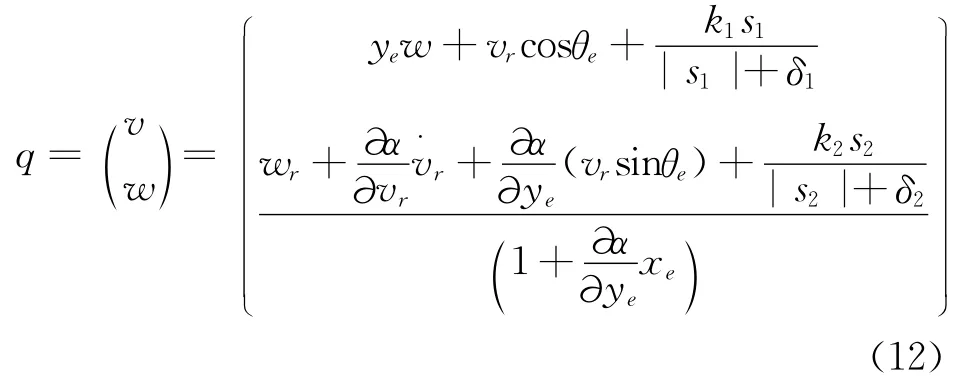
其中

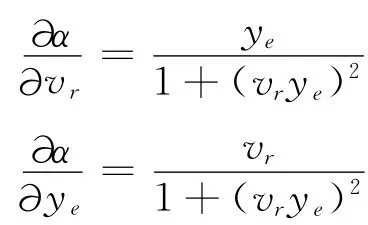
取Lyapunov函数

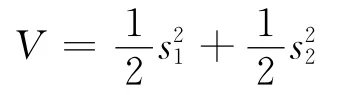
于是

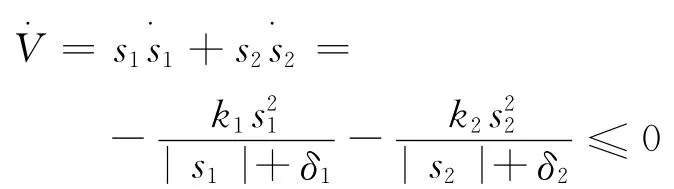
因此，可以看出系统是稳定的。

2.2 模糊滑模控制器设计

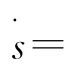
针对式（9）中设计的切换函数，选取｜s1｜（即xe的绝对值）和k1分别为模糊控制器的输入变量和输出变量。模糊子集定义为：｛Very Big（VB），Big（B），Medium（M），Small（S），Very Small（VS）｝。输入｜s1｜和输出k1的论域分别取为［0，4］和［0，100］。根据相关的控制经验设计了模糊逻辑控制规则。当｜s1｜为VB时，则系统运动点与切换面的距离较远，需要一个较大的趋近速度k1，即k1也应为 VB；而当｜s1｜为 VS时，系统运动点与切换面距离很小，于是只需要较小的k1，从而削弱抖振，即k1应为VS。模糊逻辑控制规则见表1。

表1 控制规则表

3 仿真实验研究

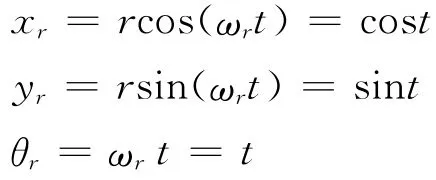
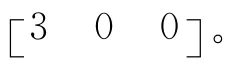
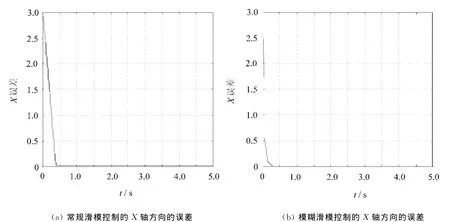
图2 常规滑模控制和模糊滑模控制的X轴方向的误差

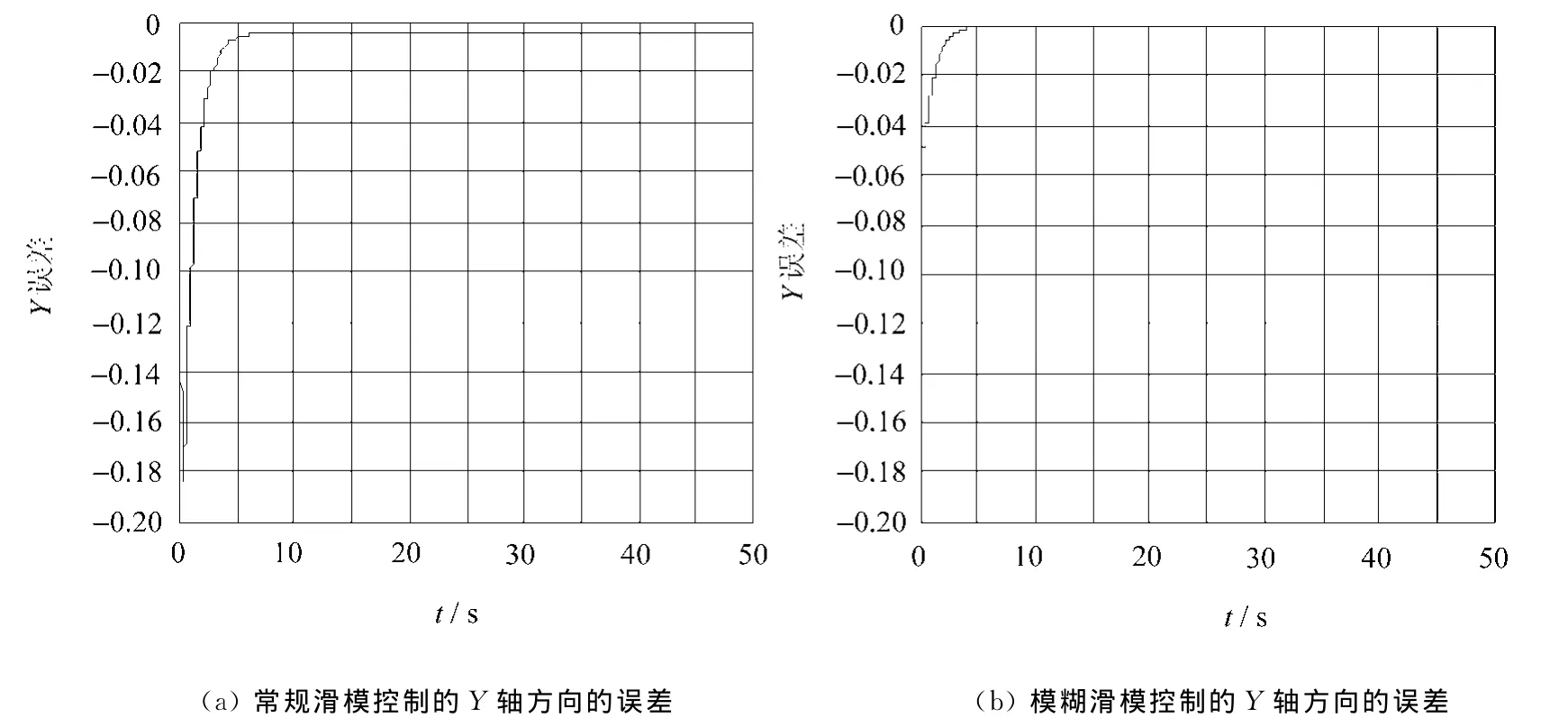
图3 常规滑模控制和模糊滑模控制的Y轴方向的误差

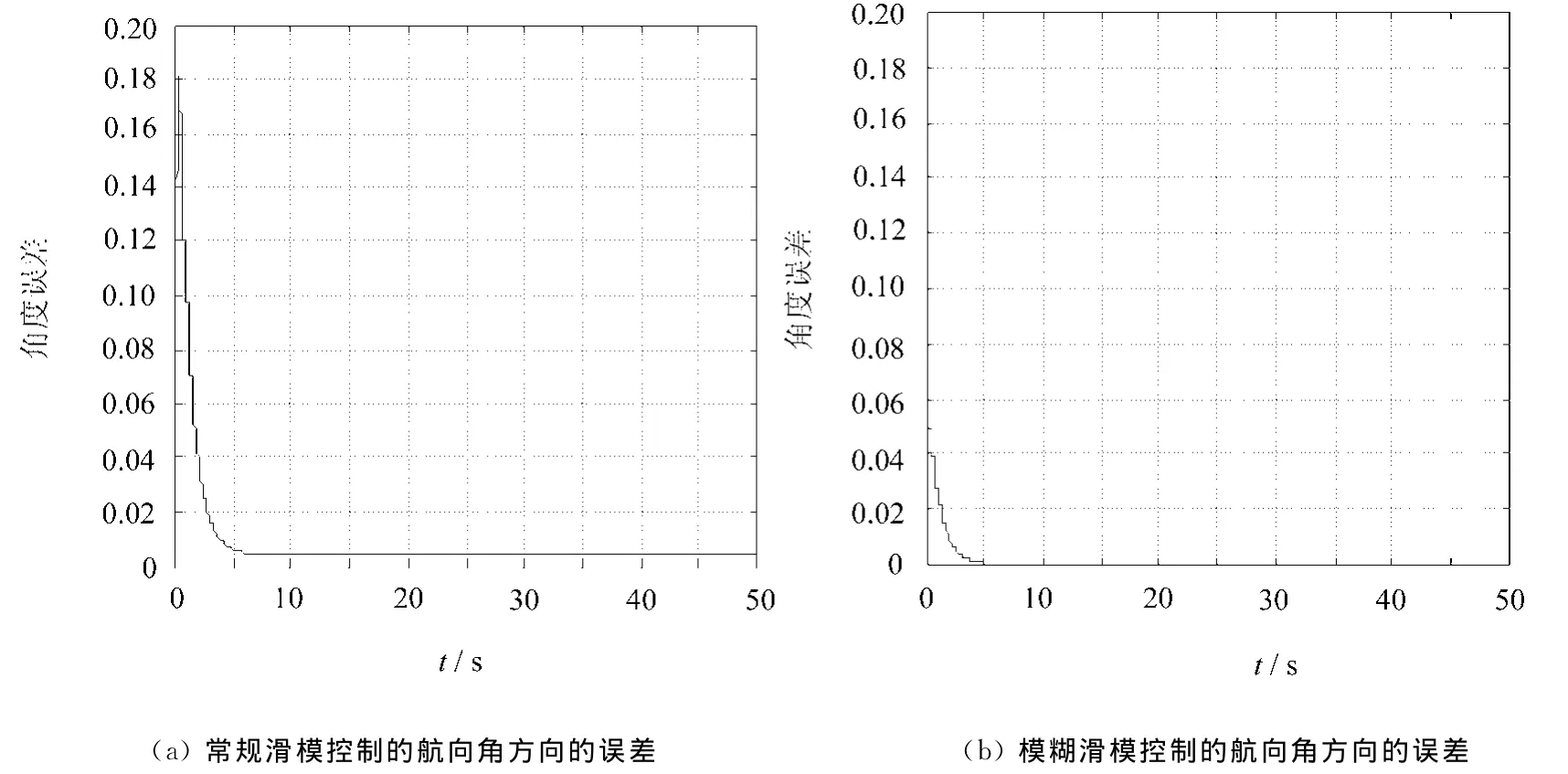
图4 常规滑模控制和模糊滑模控制的航向角方向的误差

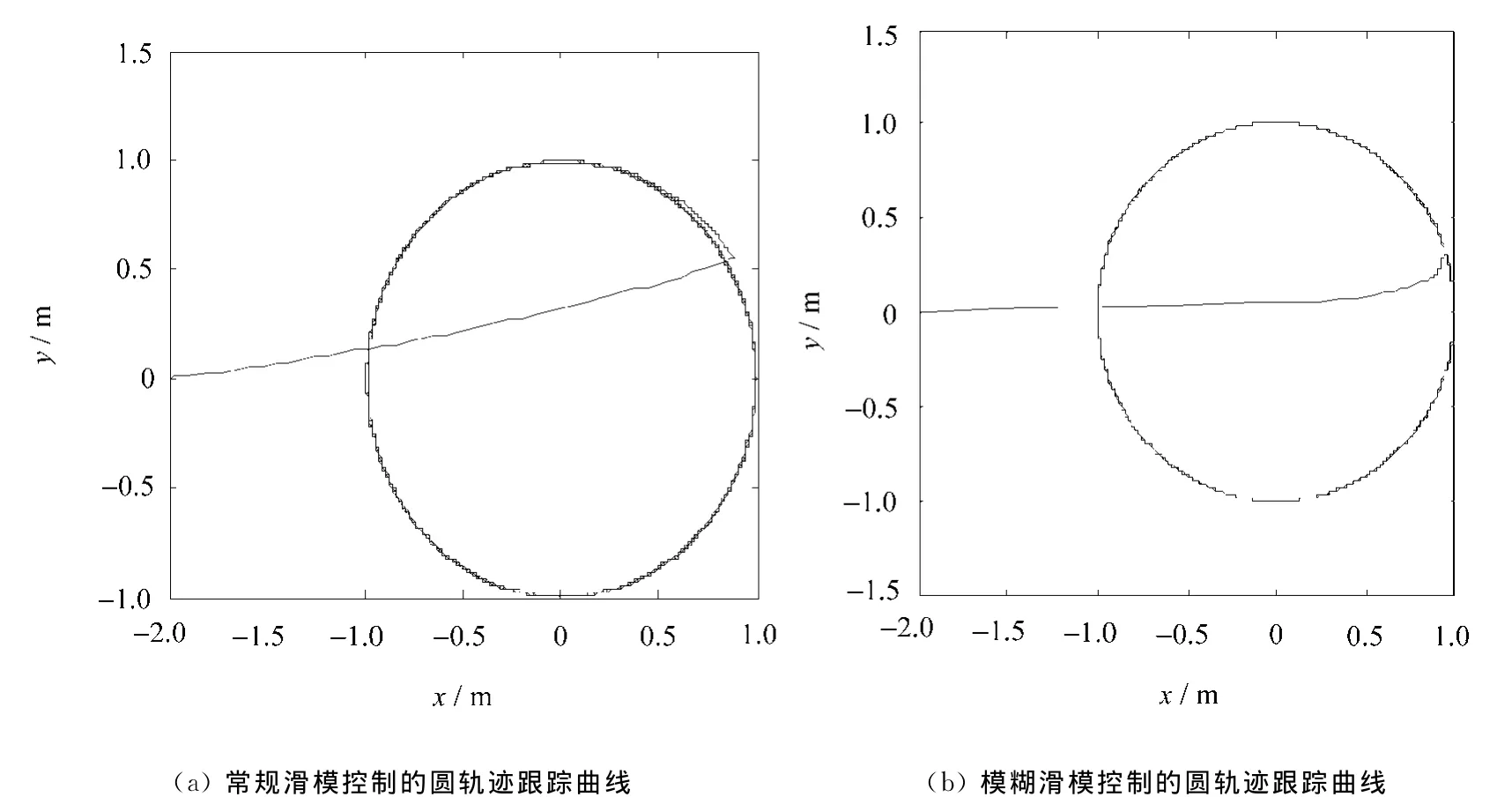
图5 常规滑模控制和模糊滑模控制的圆轨迹跟踪曲线

从图2可以看出，在前0.5s时间内常规滑模控制在X轴方向的误差（xe）明显大于加入模糊滑模控制后的误差，加入模糊滑模控制后xe最终为零，且趋近时间减小。

从图3可以看出，Y轴方向的误差（ye）幅值在常规滑模控制时最大幅值为0.18，加入模糊控制后最大幅值为0.05，幅值明显减小，最终ye为零，抖振的抑制作用加强。

同理，从图4可以看出，加入模糊控制后θe的振动幅度明显减小，最终为零，且趋近时间大大减小。

图5对比图表示的是圆轨迹位置跟踪图，由于模糊滑模控制的3个误差值均能最终达到零。其跟踪效果要远远好于常规滑模控制。

4 结 语

以非完整轮式移动机器人为研究对象，基于变结构控制思想提出了模糊滑模控制器的设计方法，并针对滑模控制的抖振问题构建模糊趋近律。通过MATLAB仿真软件在常规滑模控制和模糊滑模控制两种情况下，对圆形轨迹跟踪问题进行了仿真对比实验研究。由仿真结果可知，提出的模糊滑模控制方法不但大大削弱了滑模控制存在的抖振现象，同时，也很好地实现了期望轨迹的跟踪，改善移动机器人的控制系统性能，该方法是可行、有效的。

［1］吴卫国，陈辉堂，王月娟.移动机器人的全局轨迹跟踪控制［J］.自动化学报，2001，27（3）：326－331.

［2］任慧荣.类车移动机器人轨迹跟踪控制方法研究［D］：［硕士学位论文］.天津：天津大学，2008.

［3］Gu D，Hu H.Nerual predictive control for a carlike mobile robot［J］.Robotics and Autonomous Systems，2002，39（2）：73－86.

［4］陈少斌，蒋静坪.四轮移动机器人轨迹跟踪的最优状态反馈控制［J］.浙江大学学报，2009，43（12）：2186－2190.

［5］Kunar U，Sukavanam N.Backstepping based trajectory tracking control of a four wheeled mobile robot［J］.International Journal of Advanced Robotic Systems，2008，5（4）：403－410.

［6］张细政.王耀南.基于滑模观测器的永磁同步电机变结构鲁棒控制［J］.控制与决策，2009，24（1）：157－160.

［7］Liaw D C，Liang Y W，Cheng C C.Nonlinear control for missile terminal guidance［J］.Journal of Dynamic Syatems，Measurement and Control，2000，122：663－668.

［8］张元涛，石为人，邱明伯.基于非线性干扰观测器的减摇鳍滑模反演控制［J］.控制与决策，2010，25（8）：1255－1260.

［9］Jiang K，Zhang J G，Chen Z M.A new approach for the sliding mode control based on fuzzy reaching law［C］／／Intelligent control and Automation，Proceedings of the 4th World Congress on，2002，1：656－660.

［10］刘金坤.机器人控制系统的设计与MATLAB仿真［M］.北京：清华大学出版社，2008.

［11］杨敏，刘克平.柔性机械臂动力学建模与控制方法研究进展［J］.长春工业大学学报：自然科学版，2011，32（1）：13－19.