云平台中多任务分配集成蚁群优化算法
姚光伟
(韩山师范学院 潮州师范分院,广东 潮州 521000)
0 引 言
云计算是当今这个信息爆炸时代的研究热点,无论是传统企业,还是互联网企业都越来越重视对各种相关的数据进行分析和利用,如何对海量数据处理已成为互联网企业的核心竞争力之一。云计算的开源实现及其高容错、跨平台等众多优势,使之迅速得到众多企业的青睐,它利用分布式计算和虚拟资源管理等技术,将分散的ICT资源集中起来形成共享的资源池,改变传统用户必须购买昂贵的软硬件设备,只需向相应的服务提供商支付少量的租赁费用即可使用整个资源池的资源,从而有效地实现对互联网上资源设施等实时、按需、快捷地访问共享的计算模式。但是,这也预示着云计算的规模会非常庞大。因此,为云计算环境找到一个合理的任务分配方法已经迫在眉睫。
1 蚁群优化算法
蚁群算法是模拟自然界蚂蚁搜索行为的一种启发式仿生进化算法[1-2]。在求解复杂优化问题方面有一定优势,特别是在一些离散优化问题上具有良好优势。目前,基本蚁群算法都具有收敛速度快,且易陷入局部最优解等众多不足。同理,在云平台的资源服务中,在同一时刻越多的用户访问同一条服务路径上的资源和数据,就越容易造成相应的该网段网络负荷过重;倘若该最优路径上用户数量超出网络的承受能力,则极可能导致局部网络拥塞,严重则导致整个网络瘫痪,使厂商利益严重受损,乃至出现亏损等情况[3]。
为了改进蚁群算法使其性能更优,许多学者已经开始从各种层面或不同的策略蚁群算法提出了改进;如文献[4]中提出云模型蚁群算法(Cloud Ant Colony Algorithm,CACA),文献[5]提出混合蚁群算法(Hybrid Ant Colony Algorithm,HACA),文献[6]提出两步蚁群算法,文献[7]提出超管道蚁群算法,文献[8]提出广义蚁群算法,文献[9]提出启发式基于密度的蚁群算法,文献[10]提出倍城市当前城市号蚁群算法,文献[11]提出将蚁群算法与变异策略结合,文献[12]提出多态蚁群算法,文献[13]提出了用于连续域寻优的分组蚁群算法。然而这些算法在网络搜索中都容易陷入局部最优解,而且收敛速度和寻优精度等都有待进一步提高。
因此,如何充分利用云平台中实现云端多任务分配调度,是云计算领域的一个研究重点和难点。文中提出一种针对云计算资源中大量任务进行高效的调度研究。该算法在原有ANT算法基础上加以优化模拟,并通过数学模型运用于云计算平台中,最后通过仿真实验验证,使之能够在云计算资源高效、快捷地找到所需访问的服务节点,可有效解决ANT在网络搜索中出现停滞现象,大大提高了资源调度的效率。
2 基于蚁群优化算法的云端多任务调度
由于整个云计算的体系结构及其资源分布的实际情况都处于没有明确的机制中,任何一条线路上的网络负荷情况在不同的时刻都存在众多不可预期的动荡变幻中。部分算法单从调度性能方面进行了优化改进,但这并未充分考虑到网络负载也存在众多不可预期的大幅度变幻,这种从单方面角度去做优化改进,不仅不能高效地满足云资源调度的要求,且不利于云计算寻求资源共享和资源的最大利用率,尤其是优势资源的目标;同时,每个节点的软硬件环境、结构、吞吐量及容量等性能也都不同,使得各个网络节点和链路的负载动荡不均衡,这不仅造成资源浪费和成本增加,同时使服务的质量大打折扣。
云计算中资源异构且动态变化,在调度时随时可能有新的云资源加入,也随时有云资源故障或掉线,这种不确定性给云资源调度带来了很大困难,而蚁群算法中蚂蚁对路径的选择本身也存在诸多不确定因素,对此提出使用熵对云资源的不确定因素进行度量,提高算法收敛速度,利用信息素扩散原理更新信息素增加算法解的性能。
文中从物理学范畴中引入一个度量不确定方法的概念——信息熵,它是系统不确定性的有效度量,其定义如下:
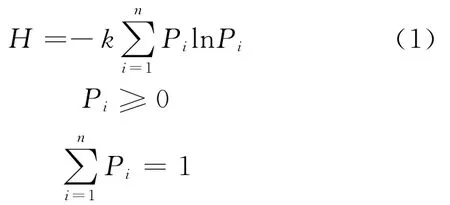
式中:P——信号源每个状态发生的概率值;
k——热 力 学 常 量 玻 尔 曼 常 数,k=1.380 650 5×10-23J/K。
当所有蚂蚁释放信息素后,通过式(1)计算系统的信息熵H(t):
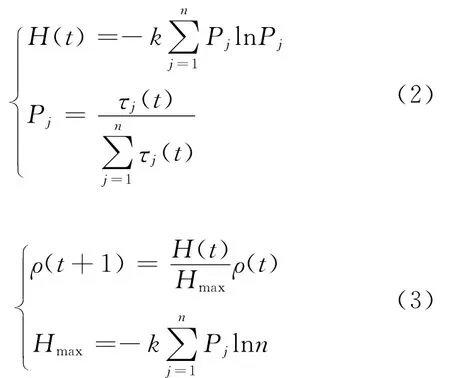
式中:ρ(t)——随时间t而改变;
n——资源j的内存总和。
根据式(2)将蚂蚁个体在一个搜索周期后更新系统信息熵,通过式(3)调节挥发因子。
这样伴随着系统信息熵调节挥发因子变化,使该算法能够通过挥发因子的变化自适应收敛调节,可有效避免蚂蚁在网络搜索中陷入局部最优解,从而提高算法效率。
2.1 算法描述
设云计算环境下t刻节点域slave表示为G=(V,E),V为所有云节点,m和E 分别代表搜索蚂蚁数目和所有链路集合。τsm(t)为t时刻路径(s,m)上的信息素,ρ表示信息素挥发系数,(1-ρ)表示信息素残留因子[14]。
s[s][m](s,m=0,1,2,…,m-1;i≠j)的计算如下:

dsm——以节点i为中心,到其它m-1个节点的最大距离。
据此结果,首先置初始时刻各条路径(s节点到m节点)上的信息量如下:

式中:Csm——节点sm路径上信息素的浓度初始值;
E——节点的个数;
S——CPU的速度。
针对搜索蚁群的做法是:蚂蚁k(k=1,2,…,n)在t时刻搜寻路径,从其中节点s出发,以一定的概率搜寻下一节点,蚂蚁k从节点s移动到节点m的概率的计算公式如下:

式中:η——权重因子,两个城市之间的距离越远,则权重值越小,ηsm=1/dsm;
tabuk——未被访问的节点集合,也就是禁忌表。
经过一次循环以后,更新每条通路上的信息素余量,对每条通路给出信息素反馈质量。该反馈质量将作为以后循环的判断依据,为蚂蚁选择通路提供信息。信息素的更新如下:


蚁群算法首先进行参数的初始化,随机选择一条路径并更新禁忌表。在第一次循环过后,更新信息素余量,然后根据式(4)计算得到的转移概率重新进行循环迭代,直到达到最大迭代次数或满足终止条件为止。
2.2 算法分析
蚁群之间通过所搜路径上的浓度变化进行互相协作和信息交换,以便迅速搜索到一条觅食的较短路径。但随着时间推移及迭代次数逐渐递增,后续的ANT所搜寻的路径逐渐趋于同一化,从而陷入云数据库中局部无休止搜寻中。而RACO算法充分兼顾了各个物理节点的时延、能量消耗等影响,并将这些负面因素作为判断条件因素;算法在开始时被初始化并保持原算法的搜索方式,随着算法的运行被更新,当各搜索的网络节点上的信息素浓度出现较为明显的变化时,便开始发挥云资源的节点上参数的有效性。
即每一次具体的分配与之前蚂蚁留在这次分配上的信息素相关。这样便可更好地消除原算法中蚂蚁个体在搜寻路径过程中“短视”的不足。使任务完成时间最短,减少资源消耗,提高云计算的效率和性能。
同时,RACO算法可利用μsm因子来自适应收敛调节蚂蚁搜索路径中信息素的浓度,可有效杜绝随机搜索陷入局部最优解难题。因为即使物理节点上ANT搜寻路径是最优解,则局部的节点更新仍能够适当地调节该路径上的信息素浓度,有效避免了后续的ANT所搜寻的路径逐渐趋于同一化,以适当抑制正反馈对全局搜寻具有积极的效用,从而实现名副其实的网络各物理节点的负载均衡自适应。
3 仿真实验分析
为了验证上述蚁群优化算法在云计算任务分配上的可行性及较好的稳定性,文中通过模拟构建云计算的局部仿真环境来测试算法的效率。
由于在云计算资源中存在众多不可预测的具体情况,且网络的拓扑结构时常变化不一,所以选择一个既有较短的时间跨度,保证任务能够被尽可能快地完成,又具有良好的负载平衡能力的云计算平台至关重要;这里主要验证改进后的蚁群算法能够高效地在云计算环境中完成计算资源搜索与分配的工作,并能够优化搜索性能,减少搜索时间,降低网络负载[14]。因此,实验是一个模拟云计算的局部域:实验设备为一般的IBM服务器及普通PC机、集中存储的磁盘阵列、SAN交换网络统一组成一个资源池,提供硬件平台资源,仿真软件为Matla7.8。
通过云计算仿真软件Matla7.8采用离散事件模拟了云计算实验环境,验证原始蚁群算法与改进后的蚁群算法在云环境中的运行情况。通过Matla7.8中的DataCenter和一系列的辅助类,模拟了云计算的计算和网络资源,以构建云计算局部环境。实验数据为实验室的模拟数据,首先随机获取1 000个个体物理资源,并对它们进行虚拟化,开始时集中存储在主服务器上,这样保证了云平台下的虚拟任务的多样性及物理资源的复杂性。由于本实验中的数据存储和传输的成本相对于CPU的计算成本而言基本可以忽略不计,因此,忽视了这部分的影响。随着时间的推移及不同数据量的逐渐增加,分别取其平均值作为算法的最终结果,该两种算法的延迟性及查询响应时间见表1。

表1 两种算法达到最优解的迭代次数及最优解对比
由表1的实验数据可以看出,改进算法无论在最优解的精确度还是收敛到最优解的速度都比原算法有很大提高,原因在于原有蚁群算法随着迭代次数逐渐增加,搜索的路径逐渐趋近于同一化,从而陷入局部最优而抑制了全局搜索能力,导致局部网络负荷过重,以致影响调度效果。而改进算法在局部更新时,不仅考虑到蚂蚁所走过的路径上的信息素,也考虑到其对周围路径信息素浓度的影响,从而兼顾到整体的网络负载均衡,所以,随着任务数和资源数增多,其优势更为明显,越能体现其最优解的性能。
4 结 语
云计算环境中如何实现将海量计算资源组成的IT资源池动态、实时、按需、合理的分配使用资源是一个非常关键的问题。因此,寻求一个好的资源调度算法至关重要。文中将改进蚁群算法(RACO)和云模型技术结合起来,进行了有力的探讨,均衡系统中各计算节点的负载,依据节点的处理能力和链路带宽状况进行不同数据量的分布,并结合网络带宽来确定任务调度最优策略,最终达到降低系统响应时间,提高了系统的整体性能与资源利用效率。实验表明,改进后的RACO可有效地运用在云平台上,很好地完成计算资源分配、搜寻等工作,消除搜索“短视”,均衡网络负载,迅速搜寻至最优解,对海量网络信息提取具有高效性和适应性。
[1]Dorigo M,Stutzle T.Ant colony optimization[M].Cambrige,UK:MIT Press,2009.
[2]史恒亮,唐振民,刘传领,等.基于蚁群优化算法的云数据库动态路径规划[J].计算机科学,2010,37(5):143-147.
[3]陈真.改进蚁群算法在云计算环境路径优化设计[J].江西理工大学学报,2012,33(3):66-70.
[4]段海滨,于道波,于秀芬.基于云模型理论的蚁群算法改进研究[J].哈尔滨工业大学学报:自然科学版,2005,37(11):115-119.
[5]Blum C,Valles M Y,Blesa M J.An ant colony optimization algorithm for DNA sequencing by hybrid-ization[J].Computers & Operations Research,2008,35(11):3620-3625.
[6]Wang H S.A two-phase ant colony algorithm for multi-echelon defective supply chain network design[J].European Journal of Operational Research,2009,192(1):243-252.
[7]Carpaneto E,Chicco G.Distribution system minimum loss reeonfiguration in the hypercube ant colony optimization framework[J].Electric Power Systems Research,2008,78(12):2037-2045.
[8]Hou Y H,Wu Y W,Lu L J,et al.Generalized ant colony optimization for economic dispatch of power system[C]//Proceedings of the 2002International Conference on Power System Technology.Washington,DC:IEEE Computer Society,2002,1:225-229.
[9]Cheny F,Liuy S,FAqTAH C A,et al.HDACC:A heuristic density based ant colony clustering algorithm[C]//Proceedings of the IEEE/W IC/ACM International Conference on Intelligent Agent Technology.Washington,DC:IEEE Computer Society,2004:397-400.
[10]Nalmi H M,Taherinejad N.New robust and efficient ant colony algorithms:Using new interpretation of local updating process[J].Expert Systems with Applications,2009,36(1):481-488.
[11]Yang J H,Shi X H,Marchese M,et al.An ant colony optimization method for generalized TSP problem[J].Progress in Natural Science,2008,18(11):1417-1422.
[12]徐精明,曹先彬,王煦法.多态蚁群算法[J].中国科学技术大学学报,2005,35(1):59-65.
[13]李秋云,朱庆保,马卫.用于连续域寻优的分组蚁群算法[J].计算机工程与应用,2010,46(30):46-49.
[14]陈真.基于蚁群优化算法的云计算资源分配[J].青岛科技大学学报,2012,33(6):619-624.

