基于有限差分的2.5维直流电阻率法的改进

蒋 亮， 邓居智， 陈 辉， 祝福荣， 孟小杰

(东华理工大学放射性地质与勘探技术国防重点学科实验室，江西 南昌 330013)

直流电阻率法根据地下岩石的导电性差异，通过记录观测和研究激发人工电流场所得到的数据规律来反演地下结构。在高精度正演计算中，应用有限差分法进行计算时，受傅里叶系数和边界条件的影响较大，会导致计算精度不够高(张华等，2012)。Dey等 (1979)开发的一款2.5D模型算法，在这种方法中，地质描述为2D，点电源为三维源，而不必明确3D模型，这是基于在很多地质情况下，可以假设地下的导电性在一维结构是不变的这一理论(吴信民等，2013)。根据这种模型理论，在应用有限差分的基础上，对公式中的傅里叶系数进行改进;采用边界校正，对其边界条件进行优化，使正演效果收边界条件的影响更小。

1 2.5维直流电阻率的理论推导

设点电源为水平地面上的A点，电流强度为I，用j表示电流的密度矢量，E为电场强度，u表示电位，ρ为岩石的电阻率，σ=1/ρ表示介质电导率，由稳定电流场的特性可以得到:

根据(1)(2)式得:

又由电荷守恒定律导出与j和q相关的连续性方程:

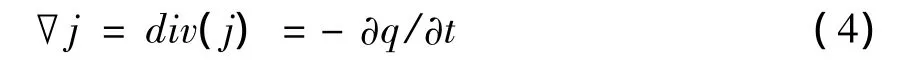
将(3)式代入(4)式得到U与q的分布式:

引入狄拉克函数δ，导出电位u与电流强度I的方程，将点电荷e放在(x0，y0，z0)处，最后由δ和 q得出:

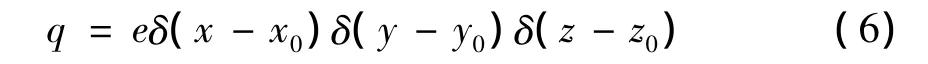
通过(5)(6)可以得到在合适的边界条件下，电导公式可以写成(杨金凤，2012):

式(7)中φ是电势场，r+r－是电流源的正负极位置。

假设(∂/∂y)σ(x，y，z)=0，那么方程(7)可以变为:

这是2.5D的电导率公式。

为了进一步求解需要进行傅里叶变换，这里傅里叶余弦变换的正向和逆向如下:

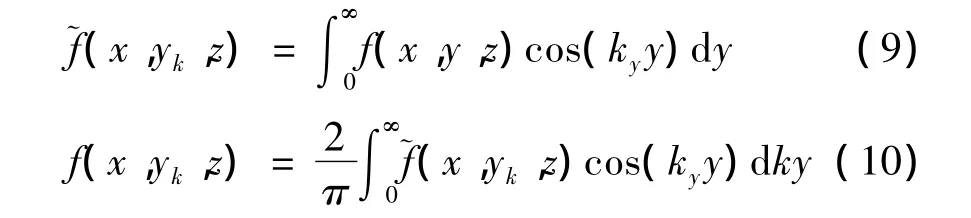
其中，ky是波数。

将上述变换代入(8)式可以得到:

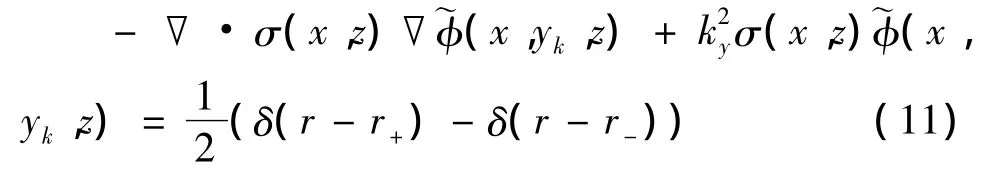
将上式用矩阵式表示为:

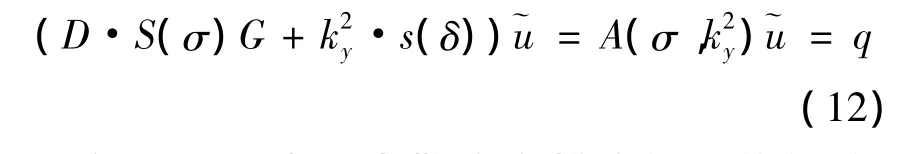
D和G分别表示为散度和梯度的二维矩阵，S(σ)是电导率，~u是转换后的电势矢量，A(σ，k2y)是前移算子矩阵，q是含有正负电流源位置的矢量。

当给定一个电导模型和波数，可以将上式改写为:

将公式(13)和(10)联合求解变形得到关于u的方程，这正是所要求的:

其中n是波数，gn是每个波数的总和(Moucha，2003)。

2 算法改进

2.1 傅里叶系数k和g的优化

要以最小的波数得到最准确的求解，需要一种优化技术，选择合适的k和g，优化k和g空间的点源，使其解决u，k和g的优化过程如下:

在一个均匀半空间的偶极源中可以得到电位:

r所处的坐标是(x，z)，rim是该源的边界位置，所以将(15)式带入到(9)式变为:

积分求解得:

K0是Bessel函数零阶修正的第二种，通过上式与(14)式进行离散反变换可得:

令Mg=v，g是包含n的向量，v是包含vi值的向量，可得到如下方程:

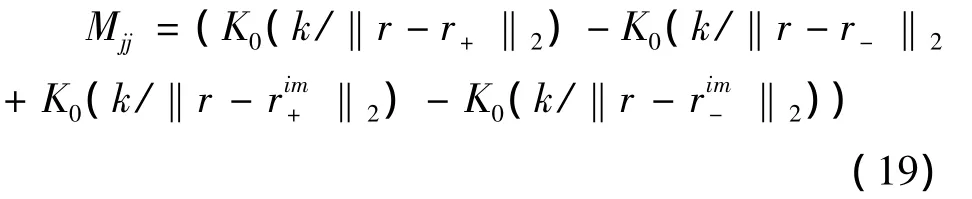
为了让误差达到最小，选择k和g使目标函数最小化，可以得出

I是一个向量，(20)式与k和g相关，而且与g成线性关系，M的出现是为了应对r的多变性，利用最小二乘法得到:

联合(19)式和(20)式得:

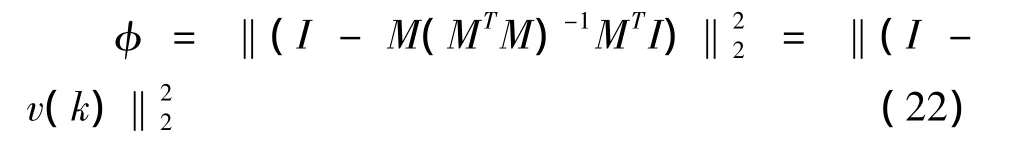
上式是一个与k相关的非线性函数。为了进一步优化，提出一个小的阻尼因子，使上式得到进一步改进:

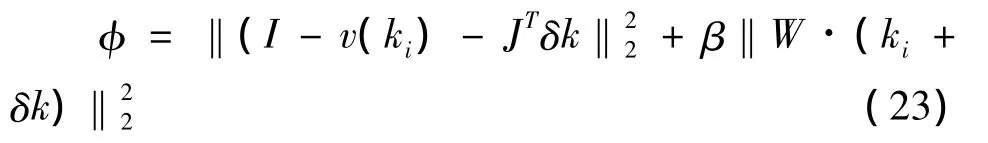
v(ki)是线性化的起点，JT是灵敏度矩阵，K是包含k值得向量，W是单位矩阵是对模型的加权，β是尽可能小的阻尼参数。对上式进行微分，得到关于K的第i次迭代方程:

定义一个新的k向量，则第i+1次迭代为:

α是为了减少(23)式迭代次数而设立的参数，当(23)式经过迭代到达理想值，就用该值来计算(20)式就可以得到 g(Pidlisecky et al.，2008)。

2.2 边界条件的优化

通过上式计算出的电压值会存在两个问题，①边界校正可以有效的解决边界效应，但要减少相关错误，需要对模型的边界网格进行填充。②奇点存在于源位置造成电势衰减迅速，故需要使这个位置得到精细的离散。为了解决上述问题，应用一个校正的源项q，使其降低BC的影响，并提出一个类似的校正因子实现减少源奇异的效果，并提高边界条件(Pidlisecky et al.，2008)。所以将(13)式代入(14)式得到:

将其变形可以得到:

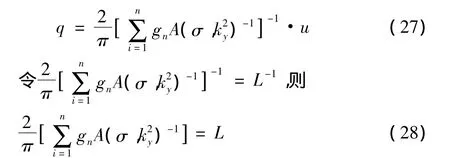
σH是稳定的电场的电导率，σT是所要求的真电导率，计算，为了量化误差，使 qcorr=L－1·uH，向量 qcorr代替 q在(15)中得到:

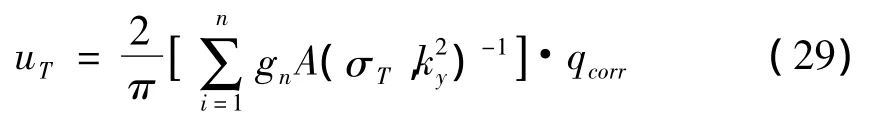
3 模型算例

这里就温纳装置建立模型进行算法验证和正演对比，温纳装置在测深过程中保持三等距，AM=MN=NB(李金铭，2005)。在温纳装置中，可以测得最佳深度是AB/6，所得测点一共有(n－1)(n－2)/6，其中n是电极数(姚文斌，1989)。故构建地下模型并将其剖分成80×30的网格，测区的剖分单元为0.5，分别建立2层均匀介质模型，高阻模型和低阻模型。为了方便验证算法的准确性，采用理想化的数值参数来构建模型。

3.1 算法验证

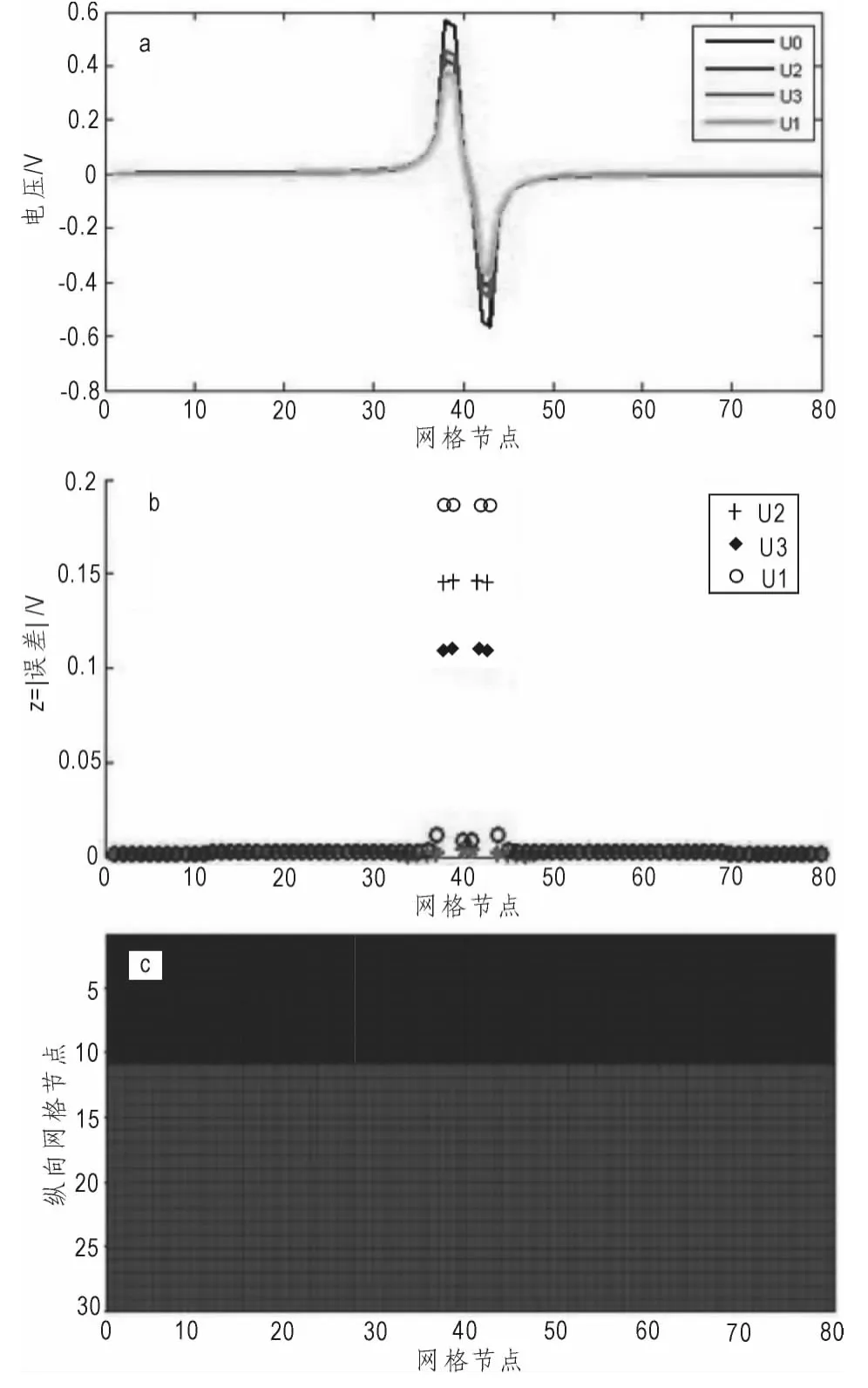
图1 算法验证对比图Fig.1 The algorithm validation comparison chart

为了方便验证算法的准确性，采用理想化的数值来构建模型，2层均匀介质的模型(图1)，第一层的电导率为σ=1 S/m，第二层的电导率为σ=100 S/m，经过计算可以得到其地表电压曲线图(U0理论曲线，U1只加入有限单元法，U2是在U1基础上加入傅里叶变换，U3是在U2基础上加入BC校正)，通过地表电压曲线可以看出，U3与U1，U2相比更加精确。最后对所得结果进行误差分析，由误差可以看出U3与U2，U1相比虽然大部分误差趋于零，但在靠近偶极源位置其误差更小，这充分说明了加入改进的傅里叶系数和边界条件，可以使计算精度进一步提高。

3.2 低阻模型

构建低阻模型(图2)，模型实际长度是30 m长，10 m深，这里剖分成80×30的网格，正方体剖分，低阻是图2中的红色区域，其大小是2×2，电导率为σ=100 S/m，周围区域为σ=1 S/m，经正演计算可以得到以x是长度，z是深度的视电阻率(图3)，其中图3a是以有限差分正常反演的结果，图3b是进一步加入傅里叶变换所产生的结果，图3c是在图3b的基础上加入了BC校正的结果。可以看出，图3b与图3a的结果基本相似略好一点，图3c与图3a，图3b相比层次感更加明显，反演结果有一定的提高，更能清晰反映出异常体所在。

图2 低阻模型Fig.2 Low resistivity model

3.3 高阻模型

构建高阻模型(其模型与低阻模型构建一样)，高阻异常其电导率为 σ=0.01 S/m，周围区域为σ=1 S/m，经计算反演可以得到其以x是长度，z是深度，的视电阻率ρ(Ω·m)(图4)其中图4a是正常反演的的结果，图4b是加入傅里叶变换所产生的结果，图4c在图4b的基础上加入了BC校正的结果。同样图4c与图4a，图4b相比层次感更加明显，反演结果有一定的提高，更能反映出异常体的现状。

4 结语

使用优化的傅里叶系数，可以有效提高数值模拟的计算精度;通过对边界进行优化，在正演过程可以使异常区域更加明显，结果受边界条件的影响更小。正演是反演的基础，希望上述改进可以对今 后反演工作有所帮助。

图3 低阻模型对比图Fig.3 Low resistance model contrast figure

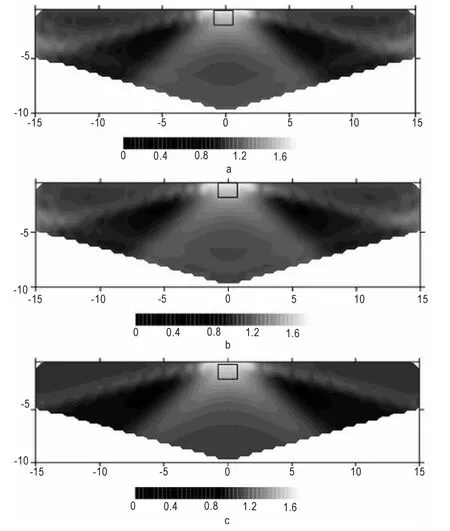
图4 高阻模型对比图Fig.4 High resistance model contrast figure

李金铭.2005地电场与电法勘探[M].北京:地质出版社:246-251.

吴信民，杨海燕，杨亚新，等.2013.论电法勘探的理论探测深度[J].东华理工大学学报:自然科学版，36(1):60-64.

杨金凤.2012.基于有限差分的直流电阻率法三维正演研究[D].南昌:东华理工大学.

姚文斌.1989.电测深数值计算和解释入门[M].北京:地震出版社:3-18.

张华，共育龄.2012.花岗岩裂隙储层各向异性高阶有限差分数值模拟[J].东华理工大学学报:自然科学版，35(4):416-421.

Dey A，Morrison H F.1979.Resistivity modeling for arbitrarily shaped two-dimensional structures[J].Geophysical Prospecting ，27:106-136.

Pidlisecky A，Knight R.2008.FW2_5D:A MATLAB 2.5D-D electrical resistivity modeling code[J].Computers ＆ Geosciences，34:1645-1654.

Moucha R.2003.Multigrid methods for forward and inverse resistivity problems in geophysics[M].Canada:National Library of Canada:1-63.