无限增益多路反馈带通滤波器的研究

熊俊俏，戴璐平，刘海英

(武汉工程大学电气信息学院，湖北武汉430205)

无限增益多路反馈带通MFB滤波器具有极高的选择性和陡峭的过渡带，在信号滤波中得到广泛应用。文献［1，2］分别介绍了其传输函数的推导过程，同时其参数的选取与设计方法已有规范化的流程与参数参考表格［3，4］。传统的滤波器设计并没有考虑电路参数与信噪比的关系，这会影响滤波器性能的优化。本文通过分析MFB滤波器的参数与指标关系，采用近似处理的方法，提出了一种兼顾滤波器指标与信噪比的电路参数选取方法。

1 MFB滤波器电路与性能分析

无限增益多路反馈带通MFB滤波器电路如图1所示。图中R3和C1构成两个反馈支路，反馈强弱与信号频率有关。理想运算放大器的增益为无穷大，因此称为无限增益多路反馈滤波器。增加RC环节后，滤波器的过渡带变窄，衰减斜率增大。

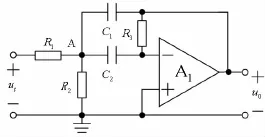
图1 无限增益多路反馈滤波器电路

令图1中A点电位为VA，则节点电位方程为

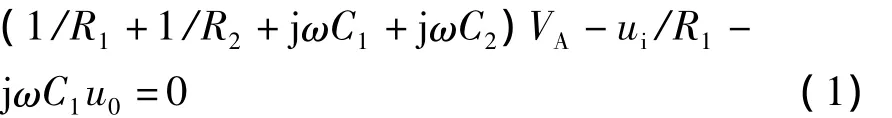
根据理想运算放大器反向输入端的“虚断”概念，可得

将上式代入式(1)，得到滤波器的传输函数为

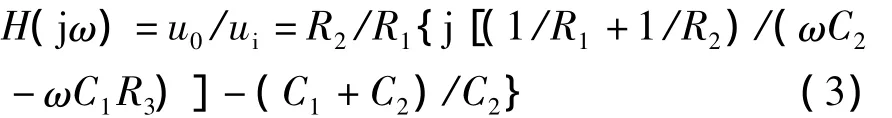
观察上式，令其虚部为零，得到滤波器的中心频率为

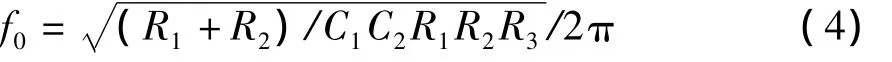
中心频率所对应的放大倍数为

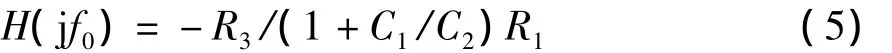
对应的品质因数Q为

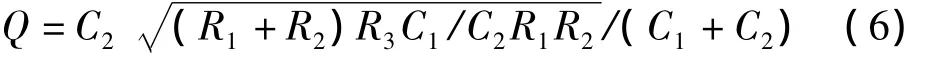
为设计方便，通常将电容取值为C1=C2=C，其对应的参数为

根据上式可见，电容C的大小并不影响带通滤波器的增益H(jf0)和品质因数Q，而电阻R3的变化会同时影响三个指标，R1、R2的并联值则影响滤波器的中心频率和品质因数，R2不影响通带增益。

2 MFB滤波器参数的选择

传统的无限增益多路反馈带通滤波器电路参数采用查表法选取［3，4］。本文通过分析，提出一种简洁的选取电阻值方法。

2.1 电容C的选取

电容的选取根据工作频率选择，依靠经验值决定，如表1所示。

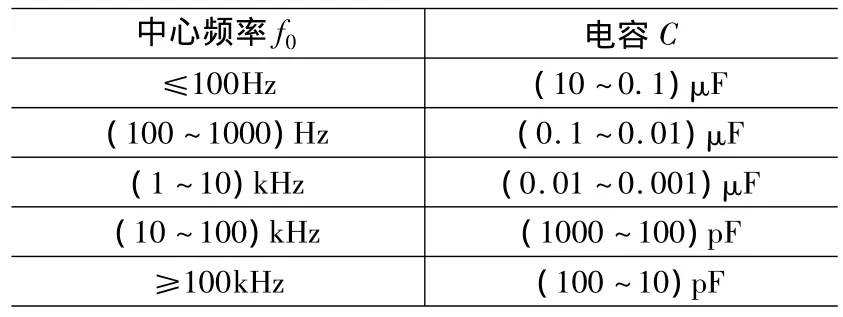
表1 中心频率与电容的取值

2.2 电阻的取值

由于滤波器的中心频率f0和品质因数Q均与电阻R1、R2的并联值有关，现在分别考虑R1R2和R1R2时电阻参数的选取。

(1)满足R1R2(工程上常取R1≥10R2)则式(7)可改为

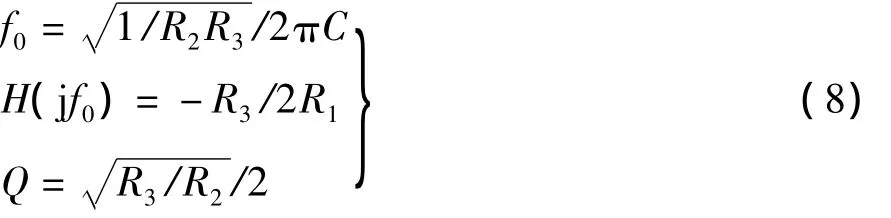
利用上式可快速获得元件参数值：

上式应用的条件是R1≥10R2，即Q≥，对应于低增益情形。

(2)满足R1R2(工程上常取R2≥10R1)则式(7)可改为

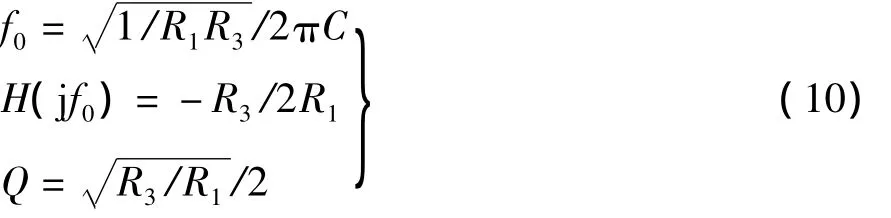
上式成立的条件是|H(jf0)|=2Q2，此时可简单快速获得元件参数值为

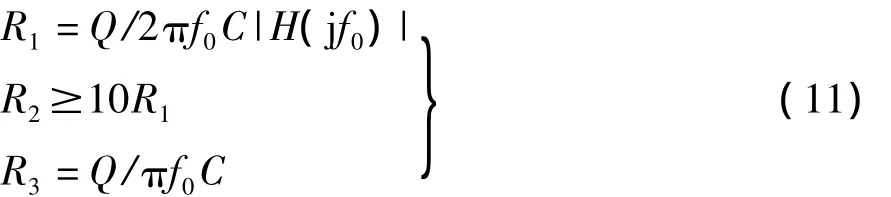
显然，R1R2只是|H(jf0)|=2Q2的特例，对应于高增益情形。

3 实际电路的分析与测试

3.1 电路原理

图2为一个中心频率为10kHz的级联无限增益多路反馈滤波器实际电路。第一级和第二级电路组成两级级联的无限增益多路反馈滤波器，第三级为低通滤波与放大电路，要求调整系统的增益。

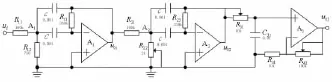
图2 中心频率为10kHz的多级MFB滤波器实际电路

根据式(4)～(6)，第一级电路的指标参数为

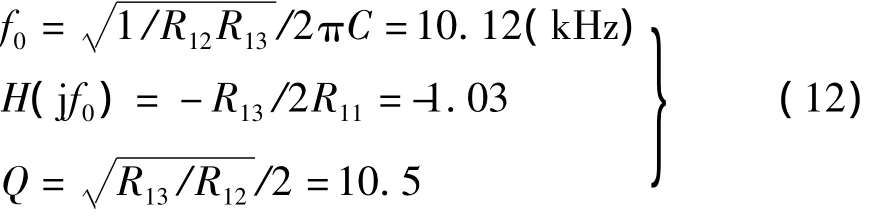
第二级无限增益多路反馈滤波器电路的R22采用电位器调整，使两级滤波器的参数相同。于是可得，该级联的带通滤波器的理论参数为f0=10kHz，H(jω0)=1，Q=16.4。

3.2 实验结果分析

从图2的电路的参数和配置看，级联的滤波器中心频率和品质因数由第一级和第二级决定，第三级实现增益要求，最大为11倍。但在实际测试中发现，输入中心频率的信号幅度须达到1V(不同的组别稍有差别)以上才能有稳定的信号输出，否则输出信号幅度会产生起伏。对此选取两组不同的R11、R21值进行分析，对应有表2所示的电路响应。表中电压为毫伏表测量的有效值(不考虑后一级放大电路，R12仍取750Ω，下同)。

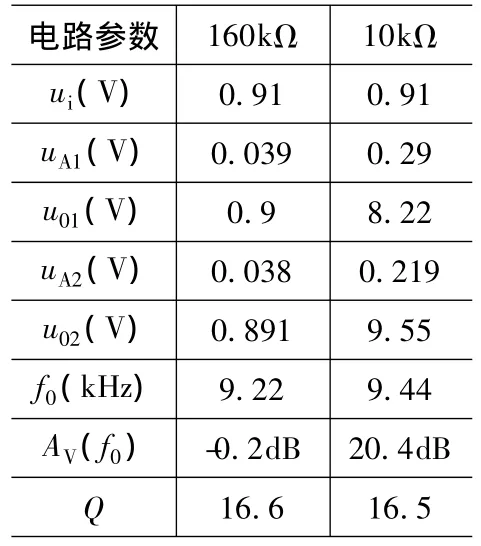
表2 不同R11=R21时的电路特性

当电阻R11=R21=160kΩ时，两级滤波器的总增益为-0.2dB，其中节点A1、A2的信号强度被衰减近28dB;当R11、R21=10kΩ 时，滤波器的总增益为20.4dB，其中节点 A1、A2的信号强度被衰减近10dB。此时中心频率有较小的偏移，但滤波器的品质因数没有变化。

从表2可以看出，R11、R21取值10kΩ时，级联的滤波器已经达到了设计指标，完全可以节省后一级放大电路;还可看出，当R11=R21取值过大时，导致信号衰减过大，引入了更大的电阻噪声，降低了输出信号的信噪比。因此，在输入信号幅度较小时，输出信号的信噪比下降，信号幅度会随噪声起伏明显变化，出现幅度不稳定的现象。所以，图2电路的输出信噪比下降和输入信号动态范围下降的主要原因是不合理。

由此可以认为：对于这种滤波器电路的参数选择应优先满足中心频率和品质因数，接着是滤波器元件参数，而增益参数作为次要参数。滤波器的增益不宜过小，以免降低输出信号的信噪比，降低输入信号的动态范围。

4 结语

本文提出了一种适合工程计算的无限增盖多路反馈带通滤波器元件参数选取方法。我们针对实际的滤波器电路调试所出现的问题进行了比较分析，从提高输入信号的动态范围与输出信号的信噪比角度出发，说明了滤波器电路指标分配原则。即：在满足滤波器频率特性的同时可尽量提高增益，避免滤波器设计过程中先衰减后放大所引起的信噪比下降问题。

［1］李永安.一种计算无限增益多路反馈滤波器增益的简便方法［J］.南京：电子工程师，2005，31(5)：31-32

［2］陈文渊，沈斌坚.二阶模拟带通滤波器的仿真和实现［J］.杭州：声学与电子工程，2010，99(3)：47-49

［3］D.E.约翰逊，J.L.希尔伯恩.有源滤波器的快速实用设计［M］.北京：人民邮电出版社，1983

［4］J.L.希尔伯恩.有源滤波器设计手册［M］.北京：地质出版社，1980