改进的基因拷贝数变异检测算法
李 平,杨洪斌,吴 悦
(上海大学计算机工程与科学学院,上海 200072)
1 概述
人类基因组在 2004年意外发现正常个体间部分基因的拷贝数存在差异,其中,2个科研小组率先公布了正常个体人类全基因组的拷贝数变异情况。拷贝数变异(Copy Number Variation, CNV)是指较之于参照基因组,DNA片段位点缺失或复制大于 1 Kb至1 Mb的结构变异[1]。拷贝数变异形式多样,包括DNA片段的缺失、嵌入、复制和复合多位点变异等。此后,相继有报道指出拷贝数变异对正常人群间的遗传变异作用。文献[2]观察基因中影响和调节细胞生长、新陈代谢的几种基因都与CNV有一定的联系。拷贝数变异检测的成果不断丰富,其中,拷贝数变异图是一新的人类基因图谱,它补充了被称为“生命之书”中残缺的章节,目的是使研究人员可以分辨基因的增加、减少和变化,从新的角度解释基因与疾病的关联[3]。
迅速发展的全基因组拷贝数扫描平台使 CNV用于全基因组关联分析成为可能,产生了大量不同的研究算法。常见的技术平台有基于大插入片段的比较基因组杂交(Comparative Genomic Hybridization, CGH),代表性寡核苷酸微阵列分析(Representational Oligonucleotide Microarray, ROMA),和单核苷酸多态性(Single Nucleotide Polymorphisms, SNP)芯片[4]。SNP 芯片是目前通量最高、使用范围最广的基因组拷贝数变异分析平台。它不仅可以有效地提高拷贝数变异检测精度,而且在一定的范围内可以增加样本,不需要额外的费用,其样本也可反复使用,增加效率。在高通量的基因检测中,数据量更为庞大,检测精确度更高[5]。最常见的 SNP阵列数据来自商业公司 affymetirix和illumina,他们所出售的 SNP阵列数据在检测 CNV区域有着一定的竞争力[6]。
cnvPartition算法是基于 SNP芯片上的常见算法[7],可以有效地检测出隐藏性小片段变异 CNV和新的CNV。但是由于SNP数据位点较多、数据量庞大、运行负担较大且速度缓慢,普通地运行检测算法也需要很好的软硬件支持。因此,改进 cnvPartition算法,提高其速度又能保持较好的运行结果是十分必要的。cnvPartition算法是基于三元分割的原理,为了找出显著变异点,需要不断进行测试。二元分割是一种简单快速的分割方法,可以快速地找出分割断点,但忽略了隐藏在大片段中的小片段检测。因此,本文基于分割原理[8]提出一种改进 cnvPartition算法的基因拷贝数变异检测算法,有效地结合了二元分割和三元分割[9]。
2 相关方法
2.1 cnvPartition算法
cnvPartition算法是使用 LRR(Log R Ratio))和BAF(B Allele Frequency)数据定义出基因组上拷贝数发生变异的区域。cnvPartition算法通过循环查找基因数据断点的方法去确定拷贝数变异和其存在的位置,其目的是在染色体内得到均值不同于其余区域的CNV区域。该算法可以分为:检测断点得到变异段和计算断点间片段的CNV值。在查找断点时,通过循环比较,确定可疑变异区域,进而查找确定变异断点[10]。该方法可以有效地检测出隐藏在大变异片段中的小型片段,但是需要重复比较,对软硬件要求较高,对高通量数据来说运行速度较慢。
2.2 二元分割
在二元分割中,使用Z-test公式检查出断点所在的位置,然后确定断点所做的分割区域[11]。断点将染色体片段分成2个部分,若断点所分割的2片段的差异度大于片段分割阈值,则肯定有一部分为变异片段。通过循环查找所有显著断点,以至于找到所有CNV变异片段。其基本过程为:在片段中根据Z-test公式查找其最大断点,判断此断点分成的2片段差异度是否大于片段阈值,以确定是否为显著断点。在显著断点分割形成的两侧片段中,再次查找出所有显著断点,最后根据显著断点所划分的变异区域计算其CNV值。
由于染色体上基因位点个数在数万个之上,因此使用Z-test算法进行计算,易发生小数被大数吞没而无法检测出隐藏在大片段中的小变异片段,有失准确性[12]。
2.3 环状二元分割算法
环状二元分割(Circular Binary Segmentation,CBS)算法是应用在CGH平台上的拷贝数变异检测算法,它是对二元分割方法的修改以提高CNV的检测效果[12]。为检测出隐藏在大片段中的小型变异区域,CBS算法将染色体两端连接起来形成环状分割,通过生成重置排列方法比较非正常数据片段。CBS可以有效地检测出小片异区域,但其运行速度易受到数据量大小限制。在 CBS算法中,重置排列计算时间与数组中位点数目的二次方位增长,对于高通量的 CGH数据将是巨大的负担。因此,这种方法在有效地检测CNV区域上也需要相应改进。
定义1(Z-test检验) Z检验是一般用于大样本(即样本容量大于 30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较2个样本的平均数的差异是否显著。
如果检验一个已知样本平均数 X与一个已知的总体平均数(μ0)的差异是否显著。Z值计算公式为:

其中,X是检验样本的平均数;μ0是已知总体的平均数;S是样本的标准差;n是样本容量。
如果检验2组样本平均数的差异性,从而判断它们各自代表的总体的差异是否显著。Z值计算公式为:

其中,X1和 X2是样本 1和样本2的平均数;S1和S2是样本 1和样本 2的标准差;n1和 n2是样本 1和样本2的容量。
定义2(断点) 假设X1, X2,…是一组随机变量,若X1, X2,…, Xv有符合分布函数 F1, Xv,…符合另一分布函数 F2,而 F1和 F2不同,则索引位置 v点即为断点[12]。
定义3(BAF) BAF表示基因位点中携带了B等位基因的杂交样本比例。在一个正常样本中,BAF有3种表达值,即0.0、0.5和 1,这分别表示位点的基因型为AA、AB和BB。当计算出BAF的值与这3个值有偏差时,说明该位置可能有拷贝数变异存在[13]。
定义4(LRR) LRR是基因位点的实际观测信号强度与期望信号强度比的lbn值。若LRR不等于0,则说明拷贝数有变化。这个函数可以测试出发生变异片段的信号强度与正常信号强度的偏异量,估计出变异强度[14]。
3 本文算法
本文将二元算法的快速性与 cnvPartition算法的准确性结合起来,可以有效地减少高通量数据中的循环比较,又保证对大型数据的详细检测,既提高速度又可保持良好的检测结果。
3.1 本文算法结构
本文算法总体流程如图1所示。
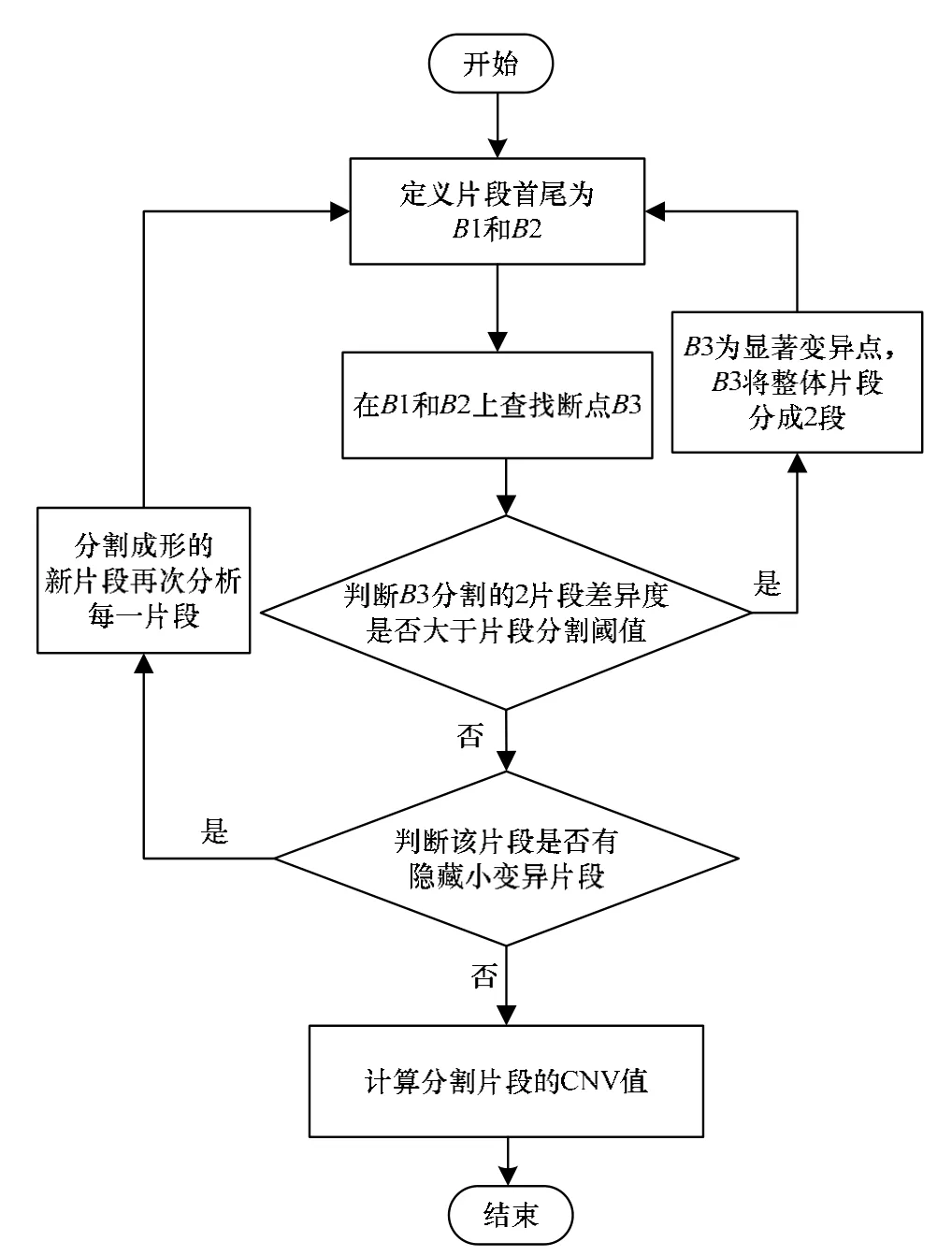
图1 本文算法总体流程
本文算法主要分为3个阶段:(1)在片段中使用二元分割方法查找断点且判断该断点是否为显著断点,是显著断点则转到阶段(2),否则转到阶段(3)。(2)根据显著断点划分的片段中用二元分割方法再次查找断点,直到无显著断点为止。(3)在无显著断点的片段中,用 cnvPartition算法查找是否有小变异片段,若有小变异片段则对新划分的片段转阶段(1)再次按二元分割查找数断点;否则将最后生成的无变异片段的片段计算其CNV值。
3.2 显著断点查找
在染色体上,每个位点的信号强度沿着染色体上的位置连续自然分布,用来检测拷贝数变异的阵列数据,也是按位点索引排序的 LRR值。若染色体上有多个断点,必然相应位点的 LRR值也发生变化。因此,本文算法最主要的内容就是根据染色体上的LRR值分布查找出所有显著CNV断点。
根据Z检验方法得到断点,将断点所划分的两区域比较其数据差异度,若差异度大于规定片段分割阈值 segment-threshold,则此断点为该片段内的显著断点。根据Z检验方法,此阈值可以应用尾部检测概率进行计算,即P值小于P(0.01)。其基本过程为:
(1)定义染色体片段X1, X2,…, Xm上T值最大的位点索引位置v为此区域内的断点B1,T的公式为:
T=max1≤i<m|Ti|
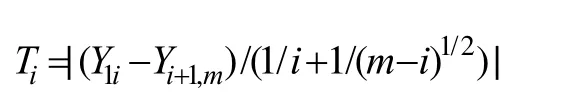
(2)计算由v所划分的染色体上2片段的差异度,并与片段分割阈值相比较。根据 Z检验方法,2片段的差异度计算方法的公式为:
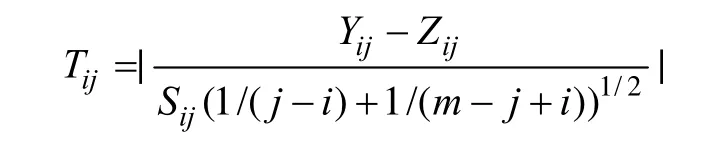
其中,Yij和 Zij表示 2片段 i到 j区域及 1到 i及j到m区域数据的平均值;Sij表示对应片段数据的平均差。若差异度大于 segment-threshold,则此断点 B1为显著断点,根据显著断点所分割的区域转步骤(2),否则转步骤(3)。
(3)在B1的2侧区域内根据步骤(1)描述查找断点B2和B3,根据步骤(2)描述分别比较B2B1段与该染色体区域中其余片段的差异度和B1B2段与其余片段的差异度,选择差异度值最大的区域端点定义为P1、P2。
(4)再次比较 P1和 P2所划分的 2相邻片段的差异度是否大于segment-threshold以确定P1和P2是否是显著断点。若P1和P2中至少有一个显著断点,则转步骤(1),否则转步骤(5)。
(5)该片段内没有显著断点,也即此区域内没有拷贝数变异片段。计算此片段的CNV值[12]。
3.3 CNV值计算
对于无显著断点的区域内,计算其CNV值,检测出CNV变异区域。根据染色体位点检测的LRR值和BAF值,与14个标准的正常位点值相比较计算每位点的初步拷贝值。对每一分割片段区域内,对每一假定的拷贝值(0~4),计算所有位点的 lbLk值之和,和值最大的 k值即为这一区域的拷贝数值。对于CNV值不为2的区域,对每个CNV值计算一个置信度。置信度的计算形式为区域为所有lbLK之和减去区域内所有位点的lbL2值[11]。
3.4 时间复杂度分析
在 cnvPartition算法中,确定一个显著断点至少需要比较7次。若一个区域内只有n个显著断点,至少需要比较 7×n次,同时为检查 n个断点所划分的n+1个区域内是否还有断点,共需要7×n+7×(n+1)次比较。在本次segcnv算法中,n个显著断点的区域中需要比较至少n+7×(n+1)次。当n值不断变大时,其算法运行时间提高7×(2n+1)/(8n+7)≈2倍。
4 实验结果与分析
本文将描述使用上述算法的运算结果,在Windows系统下使用 C++语言编写运行程序。通过infinium HD芯片得到的白血病样本数据阵列来进行模拟本文算法。这里选择了8份3号染色体下同种样本的数据去考虑在不同数据量下 cnvPartition和本文算法在运行时间和运行结果上的比较。
本文实验从运行时间和运行结果两方面考查本文算法的效率。图 2为本文算法与cnvPartition算法的相对运行时间比较。
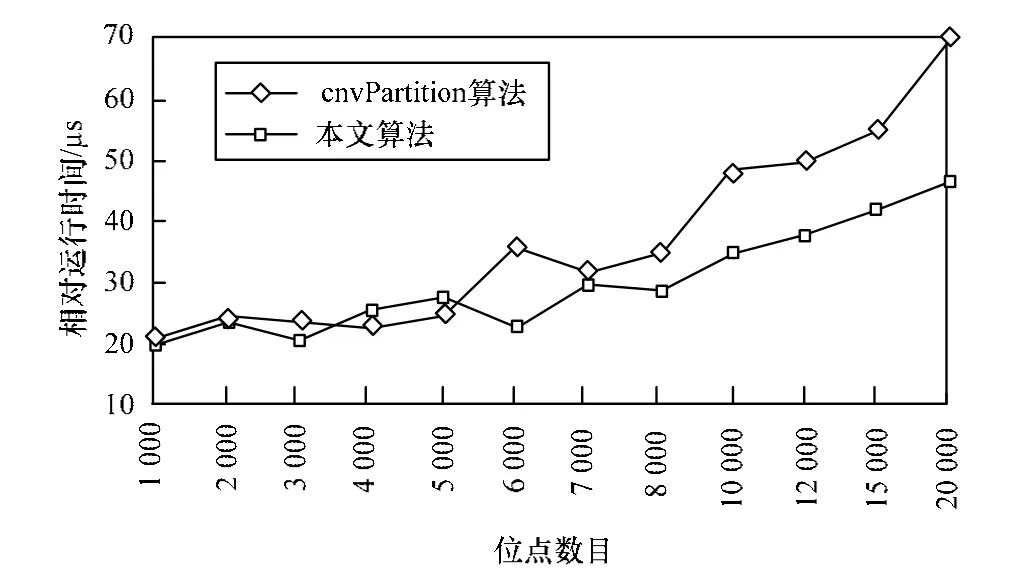
图2 2种算法的相对运行时间比较
从图2可以看出,cnvPartition算法在数据量较少时,可以维持着较短的运行时间。但是随着数据量的增加,运行时间不断增长,以至于在成千上万的高精度数据中,成为限制本文算法效率的重要原因。由二元分割算法和 cnvPartition算法结合的本文算法,其运行时间低于 cnvPartition算法。当数据量不断增大时,其运行时间并没有表现出指数增长,仅表现出一定的比率增长。相对于原算法,本文算法在高数据量运行时可以保持较低的运行时间,在位点数增加时,最高可提高将近50%的速度。这对于提高cnvPartition算法的效率是至关重要的。
2种算法分割片段数目比较如图3所示。
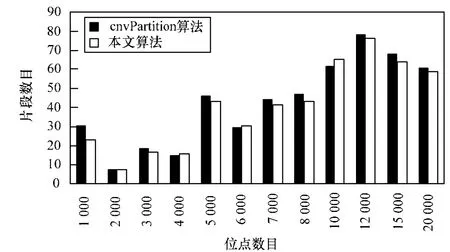
图3 2种算法分割片段数目比较
由图3可以看出,由于cnvPartition算法在选择显著变异断点时,进行详细检查,其可以有效地将大片段数据根据其所在的位置进行有效的划分,得到更多小型片段。且本文算法即保留了 cnvPartition良好的仔细检测模式,同时,对于显著断点的检测提高了检测速度,维持了良好的检测算法,非常有利于检测出小片段的CNV变异。
5 结束语
基因拷贝数变异作为影响人类疾病的一个重要因素已经得到了广泛关注。高通量的检测平台和有效的检测算法已经被提出,目前着重于提高算法的效率。研究发现,CNV的基本类型都为小型变异片段,因此,有效地检测出小型变异对CNV的研究具有重要意义。本文提出一种改进的基因拷贝数变异检测算法。通过改进 cnvPartition算法,减少部分内部循环比较,提高运行的速度,使用断点分割的原理,又重视对于小变异片段的检测。实验结果表明,该算法在高数据量运行时可以保持较低的运行时间,保持cnvPartition算法在检测隐藏性小片段变异上的良好效果。今后将着重研究染色体上位点数量庞大所造成计算速度下降的问题。
[1]吴志俊, 金 玮.拷贝数变异: 基因组多样性的新形式[J].遗传, 2009, 31(4): 339-347.
[2]陈执中.人类基因组拷贝数变异与新药研究开发[D].上海: 中国科学院上海冶金研究所, 2000.
[3]谭 琪, 曾凡一.遗传变异的又一来源: 拷贝数变异[J].生物技术通迅, 2009, 20(3): 396-398.
[4]孙玉琳, 刘 飞, 赵晓航.拷贝数变异的全基因组关联分析[J].生物化学与生物物理进展, 2009, 36(8): 968-977.
[5]Daniel A P, Jennie M L, Frank J S, et al.High-resolution Genomic Profiling of Chromosomal Aberrations Using Infinium Whole-genome Genotyping[J]. Genome Research, 2006, 16(9): 1136-1148.
[6]Winchester l, Christopher Y, Ragoussis J.Comparing CNV Detection Methods for SNP Arrays[J].Briefings in Functional Genomics and Proteomics, 2009, 8(5):353-366.
[7]Myungjin M, Jaegyoon A, Chihyun Y Y.A Computational Approach to Detect CNVs Using High-throughput Sequencing[C]//Proc.of the 9th IEEE International Conference on Bioinformatics and Bioengineering.[S.l.]:IEEE Press, 2009.
[8]Chihyun P, Youngmi Y, Jaegyoon A, et al.A Novel Approach to Detect Copy Number Variation Using Segmentation and Genetic Algorithm[C]//Proc.of ACM Symposium on Applied Computing.New York, USA:ACM Press, 2009.
[9]Erez B Y, Yonina E.A Fast and Flexible Method for the Segmentation of aCGH Data[J].Bioinformatics, 2008,24(16): 139-145.
[10]Gaellla M, Benjanim R S, Montserrat G C, et al.Assessment of Copy Number Variation Using the Illumina Infinium 1M SNP-array: A Comparison of Methodological Approaches in the Spanish Bladder Cancer/EPICURO Study[J].Human Mutation, 2011, 32(2): 240-248.
[11]Illumina Corporation.DNA Copy Number and Loss of Heterozygosity Analysis Algorithms[EB/OL].(2010-11-21).http://www.illumina.com.
[12]Adam B, Olshen E, Venkatraman S.Circular Binary Segmentation for the Analysis of Array-based DNA Copy Number Data[J].Biostatistics, 2004, 5(4): 557-572.
[13]Venkatraman E S, Adam B O.A Faster Circular Binary Segmentation Algorithm for the Analysis of Array CGH Data[J].Bioinformatics, 2007, 23(6): 657-663.
[14]Illumina Corporation.DNA Copy Number Analysis Algorithms[EB/OL].(2010-08-21).http://www.pasteur.fr/ip/portal/action/WebdriveActionEvent/oid/01s-00003f-00.

