基于产品定价机制的博弈模型
杨菊红,郝 睿,王旭明,霍 杰,王 鹏
(宁夏大学物理电气信息学院,银川 750021)
基于产品定价机制的博弈模型
杨菊红,郝 睿,王旭明,霍 杰,王 鹏
(宁夏大学物理电气信息学院,银川 750021)

结合博弈思想,提出了一个能反映市场经济规律的演化模型。模型突出了不同决策者的博弈行为,而市场的最终结果将决定于不同个体决策行为的综合作用。模拟结果印证了市场中的诸多经济规律,特别是产品价格随供需量的变化关系,同时也反映了不同生产背景下,两类生产者比例的多少对市场价格及供需量走势的影响。与供过于求的情形比较,供不应求的起始市场条件在任何比例下均可最终达到平衡,即该种环境更利于生产者做出正确选择,促使市场向良性方向发展。
定价机制;博弈;演化模型;供需关系
0 引言
自20世纪90年代“经济物理学”[1-2]这一概念被提出以来,在短短十几年里,该学科得到了迅速发展。所谓经济物理学,是指运用统计物理、理论物理、复杂系统理论、非线性科学、应用数学等的概念、方法和理论来研究金融市场通过自组织而涌现的宏观规律及其复杂性的一门新兴交叉学科。如将湍流、标度理论、随机矩阵定理、重正化群等理论运用于经济研究,可以得到诸多经济领域(国民财富和收入分布、金融市场的波动特性、组织与网络增长、人口经济与环境协调增长等)的重要理论成果[3-7]。近些年,蓬勃发展的复杂性研究也对经济理论提出了新的挑战,相关研究表明经济不再仅仅是市场稳定和供求均衡的结果,而是许多相互作用的个体都处于不稳定的动态过程中,每个个体都根据对未来的预测及其他个体的反应来采取行动,从而不断地学习和自适应调整的结果。
目前,经济物理学的研究主要集中在4个方面[8-9]:1)金融市场变量的统计规律研究[10-12];2)证劵的相关性、极端事件、金融风险管理和投资组合的研究[13-15];3)宏观市场的建模和预测;4)金融市场微观模型的建立[16-20]。其中金融市场微观模型的建立将更有助于深入理解市场的微观结构及价格的形成机制,该层面的研究包括基本投资者和噪声交易者博弈、逾渗模型及少数者博弈模型等。基于博弈思想并结合农产品产业特点,本文提出了一个能够反映市场价格形成机制的微观经济模型。模型重点考虑了两类生产者在未来市场价格不明确的前提下,凭借本期及前期价格走势来决定下一期的供给量。由于两类生产者采取完全不同的决策且决策行为具有随机性,所以模型给出的结果将与生产者的博弈行为紧密相关。这种过程更接近实际市场经济行为,也将为探讨投资者之间的静态博弈对市场供求关系及价格的影响提供新的启示。
1 博弈模型的建立
任何一种农产品,其价格总会因市场供求关系而发生变化,而市场供求关系又与价格、居民收入、居民消费期望、气候等诸多因素相关,为了简化模型,本文仅考虑价格与供求关系之间的反馈作用。
1.1 定价机制
市场上某种农产品的当前定价由两种因素决定:一是产品上一期的价格,二是产品本期的市场供求关系。若本期产品供大于求,则其价格将在上期价格的基础上有所下降;反之,若产品供不应求,则相应价格将会在上期价格的基础上上涨。考虑到价格的变动具有时段性特点,将时间离散化,以i表示第i个时期(计算模拟中,第i期等效于第i个计算时步),则相应的定价方程为

其中,Vi,Vi-1分别为产品第i(本期)及第i-1期(上一期)的价格,i=1,2,3,…,Ri为本期的价格影响因子,其大小取决于本期产品的供求关系,即

其中,Di为产品第i期(本期)的总需求量;Si为相应的总供给量。为体现价格影响因子对产品供求关系的响应程度,式(2)中引入系数A(A>0)。结合(1)、(2)两式,当Di-Si>0,表明产品供不应求,则Ri>0,价格上升;当Di-Si<0时,产品供大于求,此时Ri<0,价格下降。
1.2 生产预期
博弈论作为研究具有斗争或竞争性质现象的理论和方法,在经济领域得到广泛的应用。在竞争中,参与竞争的各个生产者作为博弈“局中人”为了达到各自的目标和利益,各方必须考虑对方的各种可能的行动方案,并力图选取对自己最为有利的合理方案。竞争过程中生产者将可能做出两种完全不同且具有强烈对抗的博弈策略。自然地,生产者被两种博弈策略区分为两类。一类生产者当价格下降时会减小生产规模,价格上升时则扩大生产规模,该选择总是顺应价格变动趋势而为,称之为 “顺势型”生产者。与此相反,另一类生产者作为博弈竞争方则会逆势而上,当价格下降时会扩大生产规模,而当价格上升时会缩小生产规模。相应的生产预期方程为
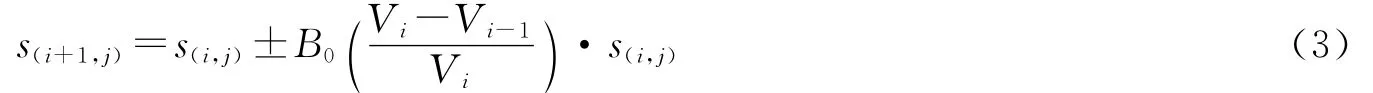
其中,s(i+1,j)代表第j个生产者在未来第i+1期的供应量,其值将围绕本期实际供应量s(i,j)上下浮动;B0(B0>0)表示价格相对变化量对生产规模的影响程度。该方程所包含的两种博弈行为具体表现为:
1)顺势型生产者:在市场价格呈下降趋势时,即Vi-Vi-1<0,生产者将降低下一期的产品供应量以减少未来亏损;而当市场价格走势上升时,Vi-Vi-1>0,生产者将扩大生产规模以提高产品供应量,其目的是为了在未来获取更多的利润。此时,式(3)中应取“+”号。该类生产者对未来市场的供求关系判断来源于本期的供求关系,即本期市场产品供大于求,未来市场也将供大于求;本期市场产品供不应求,则未来产品供求关系亦呈此态。
2)逆势型生产者:在市场价格呈下降趋势时(Vi-Vi-1<0),该生产者会逆势而行选择进一步扩大生产规模以增加产品未来供应量,以期当未来市场处于供不应求状态时获取丰厚的利润;当市场价格呈上升趋势时(Vi-Vi-1>0),为避免市场上有可能出现的供大于求状态,该生产者会缩小生产规模,降低生产量,以规避由于供大于求导致的价格下跌所造成的损失。这种选择与式(3)中的“-”号对应。可见,该类生产者对未来市场供求关系的判断与本期供求特征相反。他们对市场走势的判断是:若本期为供大于求,则下一期将会向供不应求转化;若本期供不应求,则未来市场产品将向供大于求转变,这也正是称之为“逆势型”生产者的原因。
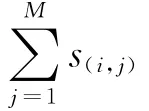
1.3 市场需求量变化趋势
一般的经济规律告诉我们产品价格变动不仅会影响未来的供应量,同时也会影响市场需求量。当价格变化呈上升趋势时(Vi-Vi-1>0),部分低收入者会退出消费行列,从而导致市场需求量降低;反之,当价格呈现下降趋势时(Vi-Vi-1<0),低收入者又会返回消费行列,致使市场需求量增加。相应的需求量方程为

其中,Di+1为第i+1期的产品需求量,C(C>0)为价格相对波动对产品需求量的影响程度。式(4)表明市场未来需求量将在本期需求量的基础上做上下调整。
至此,由方程(1)、(3)、(4)共同构成产品定价的生产者博弈模型。在给定V0,D1和S1后,模拟结果与两类生产者的比例紧密相关。值得一提的是,计算过程中,每一位生产者的决策行为具有随机性,这完全符合静态博弈思想。即在不了解市场宏观信息和博弈竞争方实施策略的背景下做出选择,而真正的市场供求关系由生产者的博弈结果共同决定。本模型将给出产品供应量、需求量、价格等变量与两类生产者选择比例之间的关系。
2 模拟结果
不同的供求关系将导致不同的价格走向,为此,本文将分别讨论本期产品供大于求与供不应求两种不同初设条件下的模拟结果。特别需要注意的是,若仅改变生产者总数,而不改变逆势者所占比例,则模型演化结果定性一致。
2.1 初始条件为供过于求
模型的初始条件为:M=200,A=0.2,B0=0.8,C=0.15,V0=28.0,D1=40 000,S1=49 705,此外,设逆势决策者所占百分比为P。
2.1.1 供需总量的变化趋势
由于初始条件为供过于求,所以价格将呈下降趋势。欲使供求平衡,需减少供给,增加需求,其中价格下降会刺激消费使需求量增加。与此同时,价格下降时,两种决策者的行为方式分别为顺势者减产,逆势者增产。当0%≤P<58%时,随着P值的增加,市场供给量呈现了从衰减到增加的变化过程,且P值越小,市场越易达到平衡,结果如图1所示。利用函数对曲线进行拟合,在不同比例下,市场总供给呈现出丰富的函数形式。具体结果为:1)P=58%时,供给量呈正比例函数增长趋势;2)70%≤P<73%时,总供给量增长且拟合函数类似幂函数;3)P≥73%时,总供给量出现不规则变化,其值围绕零点做大幅振荡;4)在其它比例下,曲线拟合类似指数函数形式,增减趋势如图1所示。
为了更多地展示模拟结果的细节,图2a,b给出了总需求量与演化时间的变化关系。结果表明,价格的下降会持续刺激需求,使需求量增加。值得注意的是,当0≤P<50%时,市场供给量与需求量变化趋势相反,且供给量随价格降低而减少,需求量随价格降低而增加,该特点与农产品的一般经济规律完全相符,此时,市场处于良性发展阶段;当50%<P<58%时,市场供给量与需求量变化虽均呈上升趋势,但经一段时间后仍可达到供需平衡;当P≥58%时,供求不能达到平衡。这一变化趋势说明,在合理范围内,生产者还可靠“薄利多销”来获取利润。一旦超过某一比例,供求关系已不能达到平衡,此时,市场已处于不稳定阶段。作为不能掌握全局信息的生产者如果在盲从效应影响下,绝大多数生产者选择逆势而为,则市场将向极度恶劣的方向发展(如P=73%),而位于其中的个体也将承担巨大的经营风险。
2.1.2 价格的变化趋势分析
逆势决策者所占比例不同时,产品价格与时间i之间的关系如图3a所示。图3a中不同曲线所对应的P值不同,表明产品价格随时间的增加呈降低趋势,这种趋势与起始条件中供过于求紧密相关。更多细节由图3 b,c表示,图3b,c表明在不同比例下价格总体趋势虽呈下降趋势,但下降程度不同。对曲线进行拟合,结果表明:1)当0≤P≤65.5%时,价格衰减且变化趋势类似指数衰减;2)当66%≤P≤73%时,价格呈现类似抛物线的下降趋势;3)当P>73%时,价格跌破甚至为负,此时曲线出现不规则变化。
价格的这一变化趋势与供需总量的变化趋势吻合。在小比例范围内,由于逆势增产人数较少以致减产总幅超过增产总幅,总供给量下降,市场在较短时间内达到供求平衡,产品价格减幅较小。在该比例范围内,P值越小,减幅越小,市场越易平衡。在中比例条件下,逆势增产与顺势减产总幅相当(原有差距未被抵消),达到平衡需要较长时间,相应的价格减幅增加。在大比例条件下,市场已不能达到平衡,此时的价格变化也已脱离了正常的价格浮动范围,表现为价格急剧下降甚至跌破为负,当然这种情况不会出现。图4给出了达到平衡所需时间随比例的变化关系。图中横轴为逆势决策者所占比例,纵轴为模型演化到供求平衡时所需要的时步数。图示结果与模型分析结果一致,其中极值点处的百分比为55.5%。
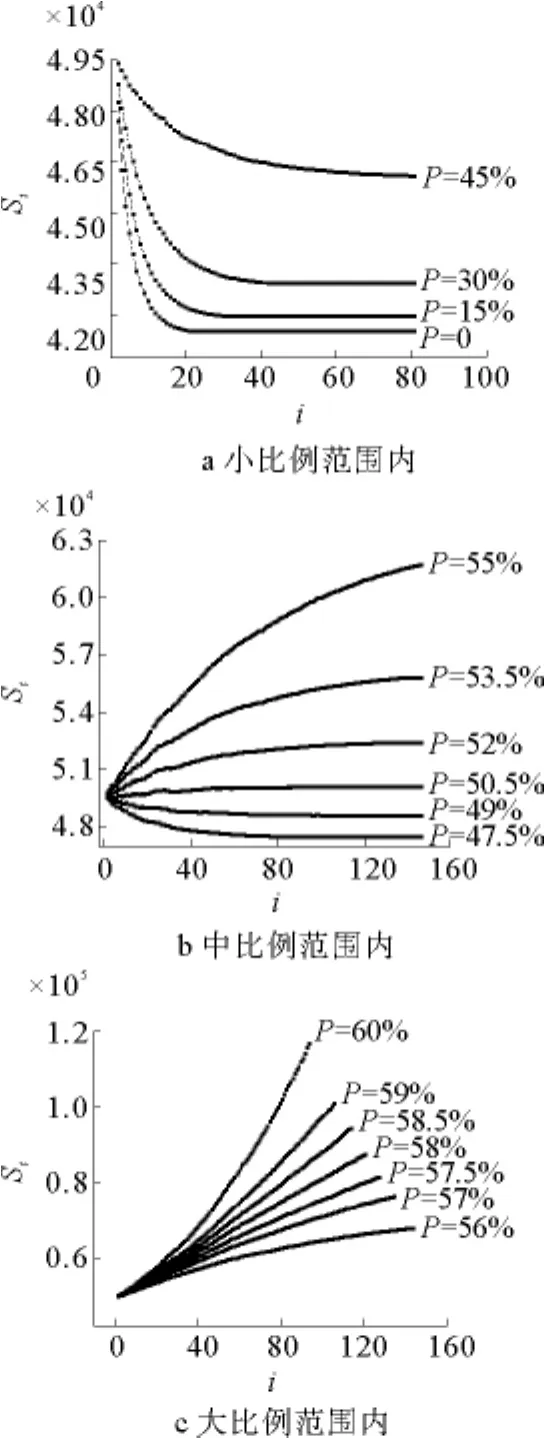
图1 总供给量随时间的变化Fig.1 Changing trends of product supply with time
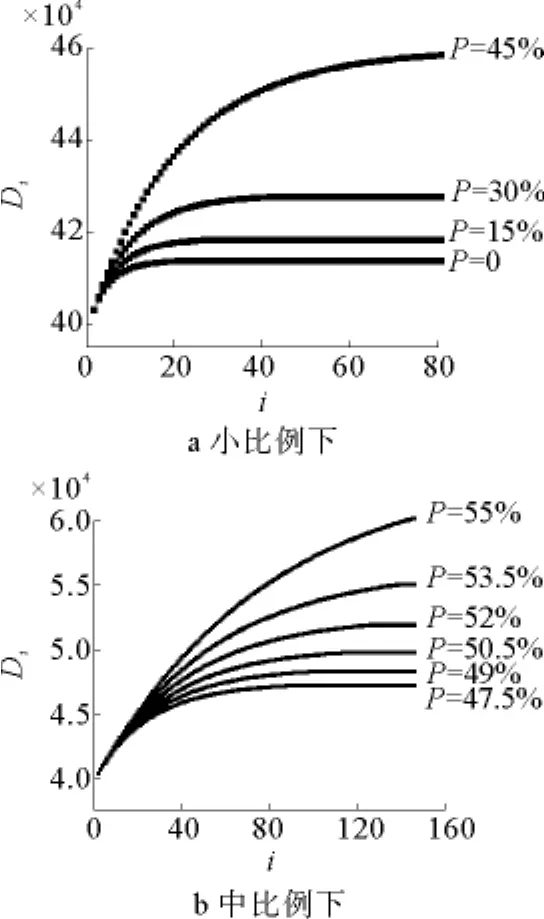
图2 需求量与时间的关系Fig.2 Changing trends of product demand with time
通过分析可知,当市场起始处于供过于求状态时,逆势者所占比例在中小范围内都可使供求关系达到平衡。不同的是小比例下价格降幅较小,中比例下降幅较大。当逆势而为的生产者占绝大多数时,突增的供给量会导致价格急剧下降,甚至跌破。此时,所有生产者选择放弃生产的概率加大,总供给急剧下滑,导致价格突增,市场进入到极其不稳定的状态,而价格波动也已脱离了正常的经济规律。这正是当模型比例超过73% 所引起图形不规则变化的原因。可见,价格急剧波动是市场不稳定的直接表现,对于生产规模较大的生产者更应谨慎决策,以免造成不可挽回的损失。
2.2 初始条件为供不应求
模型的计算初始条件为:M=200,A=0.2,B0=0.8,C=0.15,V0=16.0,D1=60 000,S1=49 705,逆势决策者所占比例依然为P。
2.2.1 供需总量的变化趋势
由于初始条件为供不应求,所以产品价格在本期内将增加。价格上升时,两种决策者对应的经营方式为顺势者增产,逆势者减产。当P值较小时,由于逆势减产的生产者占少数,所以市场供给量减幅低于增幅,总供给量呈上升趋势,如图5a所示,图中的百分比为0≤P≤50%。在该比例范围内,P值愈小,供给量总增幅越大,越易平衡初始条件下的供不应求关系,最终达到供求平衡且所需时间越短。在同等初始条件下,增加P值,即逆势减产者增加,供给关系从总增幅大于总减幅向总增幅小于总减幅过渡,相应的总供给量呈下降趋势,如图5b,该比例范围为51%≤P≤60%。继续增加P值,即P值在较大范围变动时(60%<P≤100%),总供给量如图5c所示。起初所有生产者中有相当多数采取了减产措施,所以总供给量呈陡然下降趋势。此后,由于各生产者间博弈行为的互相转化,使得供给量总降幅在博弈选择的综合作用下逐渐小于总增幅,以致总供给量上升,并最终达到供求平衡。利用函数对曲线进行拟合,市场总供给量随时间的变化关系为:1)0≤P≤50%,总供给量变化趋势类似指数增加;2)51%≤P≤60%,总供给量变化趋势类似于指数衰减;3)60%<P≤100%;演化形式呈“V”字型变化。
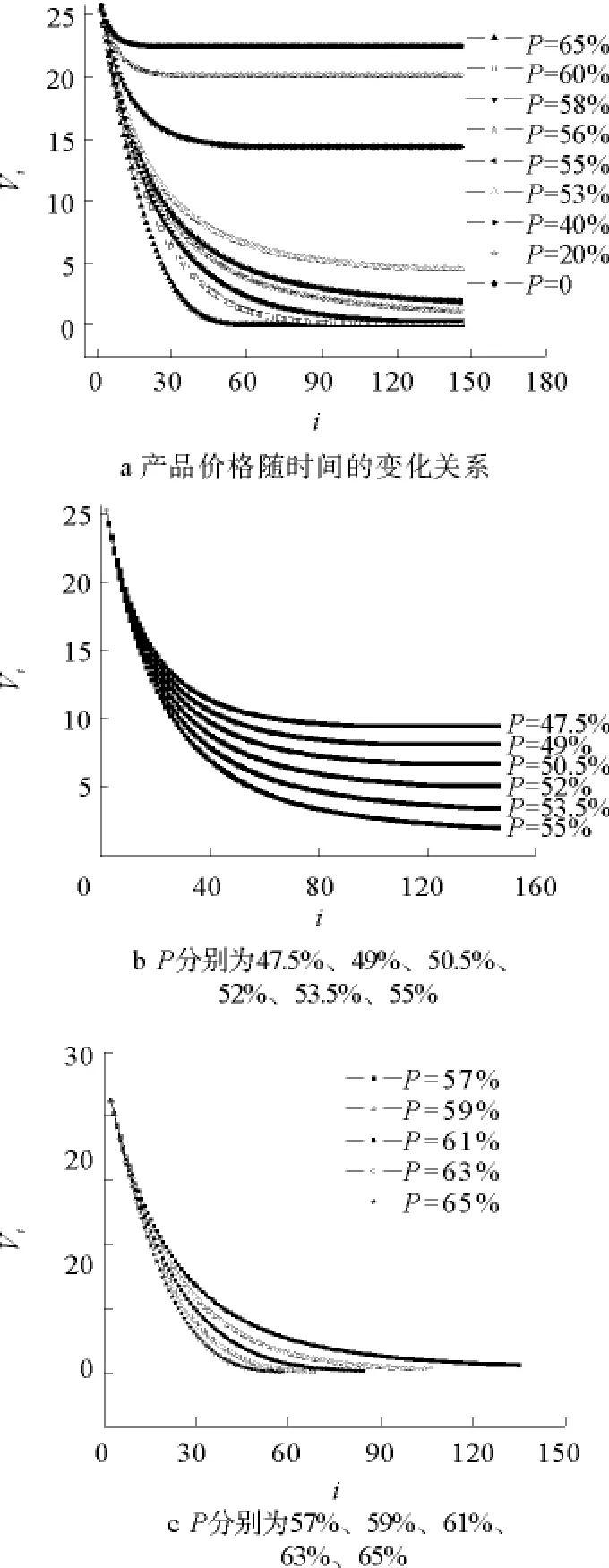
图3 产品价格随时间的变化关系Fig.3 Changing trends of product price with time
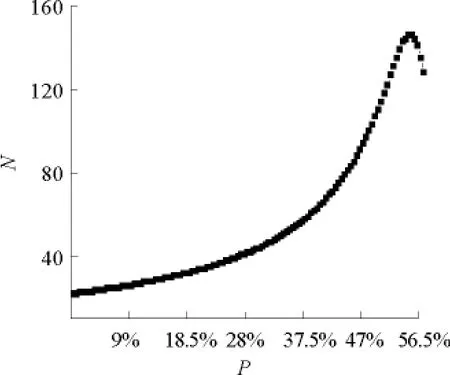
图4 模型演化时间与逆势者所占比例之间的关系Fig.4 Changing trends of model evolution time with the contrarian proportion
在价格上升过程中,市场需求量在各种比例下都将呈下降趋势,只是下降的快慢程度不同,具体结果见图6。其中,在中小比例范围内,需求量变化趋势类似指数衰减。
2.2.2 价格的变化趋势分析
起始供求关系为供不应求时,将会导致价格上升。为达到供需平衡,价格稳定,则需增加供给,降低需求。依据上述对供需量的分析,在小比例范围内(0≤P≤55%),由于供给量增幅较大,所以市场更易达到平衡,同时,受前期供不应求关系的影响,价格呈上升趋势。在该范围内,P值愈小,供需达到平衡所需时间愈短,平衡价格与起始价格愈接近,结果如图7a所示。当P>55%时,价格呈“S”型增长,如图7b。在同一比例下,价格变化经历了两边变化相对缓慢,中间变化相对剧烈的过程。起始时,价格缓慢上升。这是因为较大的P值引起的供给量降幅较大,同时价格前期历史趋势的上升使市场需求下降,且前者降幅小于后者,以致价格缓慢上升。随后,由于两类博弈者选择决策的随机性使供给量在原有基础上有所回升(图5c中供给量以较大幅度上升),而需求量始终下降。此时,价格与市场供求关系符合一般经济规律,即供给量随价格呈递增趋势,需求量随价格呈递减趋势,该趋势的出现意味着市场将向良性方向发展,价格在此过程中增幅较大。在最后阶段,回升的供给量与需求量逐渐趋于平衡,价格趋于稳定,其变化幅度相对较小。在整个变化过程中,P值越大,实现供给量由下降到升高的时间越短,市场越易走向平衡。
综上所述,起始供求关系将会导致价格,供需量的不同变化趋势。无论起始市场供求关系如何,逆势者百分比均不宜超过50%。若超过此比例,对于前者(供大于求),P值越大价格下滑越剧烈;而对于后者(供不应求),则价格会骤然上升。模拟结果还表明,初始条件为供过于求时,市场会在一定比例下失稳(P≥58%),此比例范围内,市场不会达到供求平衡;而市场初始条件为供不应求时,在任何比例下,市场均会达到供需平衡。这充分说明盲目扩大生产导致起始供求量过大,会掩盖市场原有的供求信息,使生产者决策失误的几率增加,市场向稳定方向发展的概率有所降低,在该市场环境下,决策者特别是大规模生产者的投资更需谨慎。相反地,若起始条件为供不应求时,市场总会通过调节达到供需平衡,这样的市场发展进程是健康的。这与现实生活中,某种新产品的生产规模总是从小规模开始相一致。这样的市场背景更有利于决策者做出正确的选择。
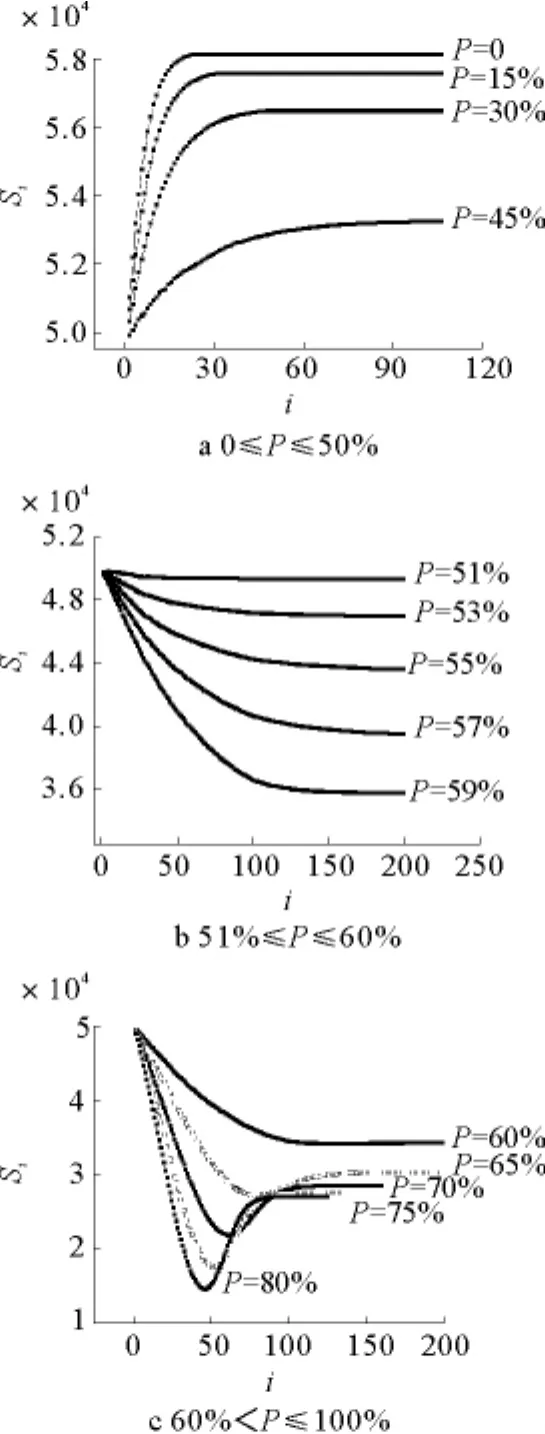
图5 总供给随时间的变化关系Fig.5 Changing trends of product supply with time

图6 需求量随时间的变化关系Fig.6 Changing trends of product demand with time
3 结论
本文结合静态博弈思想建立了一个能反映价格、供需量变化趋势的价格演化模型。模型重点考虑了生产者根据价格变化趋势所采取的不同决策行为。同时,在不同时期,生产者的博弈行为可以相互转化,市场的实际均衡由个体间博弈产生。模拟结果显示了诸多经济规律,如产品价格与需求量的变化趋势为价格与供给量呈正比,与需求量呈反比;市场中逆势而为的生产者不宜过多;更利于市场健康发展的生产背景为起始生产量满足供不应求关系等。模型还充分揭示了生产者相互作用产生的丰富的市场变化过程,其中既包括健康有序的发展过程,也包括市场走向崩溃的进程。生产者之间相互依赖、相互学习、相互模仿和相互竞争这种博弈是市场价格形成与供需平衡的动力学根源。

图7 价格随时间的变化关系Fig.7 Changing trends of product price with time
[1]Mantegna R N,Stanley H E.Scaling behaviour in the dynamics of an economic index[J].Nature,1995,376:46.
[2]Mantegna R N,Stanley H E.Turbulence and financial markets[J].Nature,1996,383:587.
[3]周炜星.金融物理学导论[M].上海:上海财经大学出版社,2007.
[4]杨晓光,马超群.金融系统的复杂性[J].系统工程,2003,21(5):1-4.
Yang Xiaoguang,Ma Chaoqun.Complexity of finance system [J].Sys Eng,2003,21(5):1-4.
[5]王有贵,郭良鹏.经济研究中的物理学[J].物理,2010,39(2):85-94.
Wang Yougui,Guo Liangpeng.Physics in the study on economics[J].Physics,2010,39(2):85-94.
[6]郑波.金融动力学的时空关联与大波动特性——兼谈中西方金融市场的对比研究[J].物理,2010,39(2):95-100.
Zheng Bo.Spatio-temporal correlations and large volatilities in financial dynamics[J].Physics,2010,39(2):95-100.
[7]黄登仕.金融市场的标度理论[J].管理科学学报,2000,3(2):27-33.
Huang Dengshi.Scaling and scaleinvariance in financial markets[J].Journal of Management Science,2000,3(2):27-33.
[8]李平,汪秉宏,全宏俊.金融物理的若干基本问题与研究进展(Ⅰ)[J].物理,2004,33(1):28-33.
Li Ping,Wang Binghong,Quan Hongjun.Some problems and progress about econophysics(Ⅰ)[J].Physics,2004,33(1):28-33.
[9]李平,汪秉宏,全宏俊.金融物理的若干基本问题与研究进展(Ⅱ)[J].物理,2004,33(3):205-212.
Li Ping,Wang Binghong,Quan Hongjun.Some problems and progress about econophysics(Ⅱ)[J].Physics,2004,33(3):205-212.
[10]Farmer J D,Shubik M,Smith E.The power(law)of Indian market:analysing NSE and BSE trading statistics[J].Physics Today,2005,58(9):37.
[11]Ding N,Wang Y G.Power-law tail in the Chinese wealth distribution[J].Chin Phys Lett,2007,24(8):2434.
[12]汪秉宏.价格的统计分析[J].广西师范大学学报,2002,20(1):19-26.
Wang Binghong.Statistical analysis of price[J].Journal of Guangxi Normal University,2002,20(1):19-26.
[13]Sornette D,Woodard R,Zhou W X.The 2006-2008oil bubble:evidence of speculation,and prediction[J].Physica A,2009,388(8):1571-1576.
[14]Sornette D,Johansen A.Large financial crashes[J].Physica A,1997,245(3/4):411.
[15]周炜星.金融市场的宏观建模和微观建模—从金融海啸与市场风险谈起[J].物理,2010,39(1):22-27.
Zhou Weixing.Macro and microscopic modeling of financial markets—sailing from financial tsunami and market risks[J].Physics,2010,39(1):22-27.
[16]Farmer J D,Foley D.The economy needs agent-based modeling[J].Nature,2009,460:685.
[17]Challet D,Zhang Y C.Emergence of cooperation and organization in an evolutionary game[J].Physica A ,1997,246(3/4):407.
[18]Dragulescu A,Yakovenko V M.Statistical mechanics of money[J].Eur Phys J B,2000,17(4):723.
[19]Johansen A,Ledoit O,Sornette D.Crashes as critical points[J].Int J Theor Appl Fin,2000,3(2):219.
[20]Lux T,Marchesi M.Scaling and criticality in a stochastic multi-agent model of a financial market[J].Nature,1999,397:498.
A Game Model Based on Pricing Mechanism
YANG Ju-hong,HAO Rui,WANG Xu-ming,HUO Jie,WANG Peng
(School of Physics and Electrical Information Engineering,Ningxia University,Yinchuan 750021,China)
An evolution model is suggested to describe the correlation between the production and the price in an agricultural commodities market.The model highlights the decisions of two kinds of producers.One follows the trend of price to determine the production,and the other goes against the stream of price.The behavior of the market will be determined by decision-making behaviors of all individuals.The numerical results show the laws that govern the real markets.Especially,they demonstrate the relation between price and quantity of supply and/or demand,and also reflect that under different production backgrounds.The proportion of two kinds of producers will influence the trend of market prices and quantity of supply and demand.Compared with the situation in which supply exceeds demand,the market that is initially in the situation that demand exceeds supply can reach a balance under any proportion of two kinds of producers.This may reveal a basic fact that the situation that demand exceeds supply contributes to the producers to make the right choice.It can promote the market to develop well.
pricing mechanism;game;evolution model;relation of supplyand demand
F224;N94
A
1672-3813(2013)02-0044-08
2012-05-14
国家自然科学基金(10965004,11265011);宁夏自然科学基金(NZ1140)
杨菊红(1985-),女,甘肃秦安人,硕士研究生,主要研究方向为人类行为动力学和复杂系统。
(责任编辑 耿金花)

