基于自然连通度的复杂网络抗毁性仿真优化研究

田 田，吴 俊，谭跃进

（1.中国人民解放军总后勤部油料研究所，北京 102300；2.国防科技大学信息系统与管理学院，长沙 410073）

基于自然连通度的复杂网络抗毁性仿真优化研究

田 田1，吴 俊2，谭跃进2

（1.中国人民解放军总后勤部油料研究所，北京 102300；2.国防科技大学信息系统与管理学院，长沙 410073）

建立了以自然连通度为目标函数的复杂网络抗毁性组合优化模型，进而提出了基于禁忌搜索的复杂网络抗毁性仿真优化算法，设计了变量编码、定义了移动操作、给出了特赦准则、设置了终止准则，给出了算法流程，最后基于仿真优化结果分析了最优抗毁性网络的结构属性，研究表明最优抗毁性网络呈现出明显的同配度关联模式，核心节点之间相互连接紧密形成“富人俱乐部”。

复杂网络；抗毁性；自然连通度；禁忌搜索；仿真优化

0 引言

因特网、交通网、电力网、通信网、物流网……，可以说，我们生活在一个网络的世界，这些我们赖以生存的网络越来越庞大，越来越复杂［1-7］。但面对越来越频繁发生的事故，我们不得不开始关注：这些复杂的网络系统到底有多可靠？一些微不足道的故障是否会导致整个网络系统的崩溃？在发生严重自然灾害或者敌对势力蓄意破坏的情况下，这些网络是否还能正常发挥作用？这一系列严峻的问题摆在我们面前，使得复杂网络系统的抗毁性研究刻不容缓、意义重大［8-10］。

网络抗毁性研究最早源于图论，早期主要应用于通信网络领域。点（边）连通度是最早被用来刻画网络抗毁性的测度指标［11］，它被定义为使得图变成不连通或平凡图所需去掉的最少节点（边）数。显然，点（边）连通度存在明显缺陷，它仅仅考虑了网络被破坏的难易程度，却未考虑网络遭受破坏的严重程度，之后很多测度被提出来弥补这个不足。例如，坚韧度［12］、完整度［13］、粘连度［14］、离散数［15］、膨胀系数［16］、核度［17-18］等等。这些改进的抗毁性测度不仅刻画了网络被破坏的难易程度还刻画了网络遭受破坏的严重程度。但是，由于这些测度指标追求对抗毁性的精确刻画而导致绝大多数指标的计算都是NP问题［19］。这意味着从计算复杂性角度来看，基于传统图论的抗毁性测度很难适用大规模复杂网络系统。

为了解决复杂网络抗毁性测度的计算复杂性以及度量精确性问题，吴俊等［20-21］最近提出建立了复杂网络抗毁性的谱测度理论与方法，所提出的自然连通度从复杂网络的内部结构属性出发，通过计算网络中不同长度闭环数目的加权和，刻画了网络中替代途径的冗余性，在数学形式上表示为一种特殊形式的平均特征根，可以从网络邻接矩阵特征谱直接导出，因此具有明确的物理意义和简洁的数学形式。相关成果发表不到一年立即得到学术界同行的关注，例如：复杂性研究领域知名学者Estrada教授对自然连通度作了详细介绍［22］，美国德克萨斯大学学者Shang跟踪研究了加权网络的自然连通度［23］以及局域自然连通度［24］。

复杂网络抗毁性研究需要回答以下3个科学问题：怎样度量复杂网络的抗毁性？什么样的复杂网络抗毁性好？怎样得到抗毁性好的复杂网络？其中，第1个问题，即复杂网络抗毁性的建模问题是基础；第2个问题，即复杂网络抗毁性的分析问题，是关键；第3个问题，即复杂网络抗毁性的优化问题，是核心，这也正是本文关注的问题。本文首先介绍复杂网络的自然连通度，在此基础上提出以自然连通度为目标函数的复杂网络抗毁性组合优化模型，进而提出基于禁忌搜索的复杂网络抗毁性仿真优化算法，最后分析最优抗毁性复杂网络的结构属性。

1 复杂网络的自然连通度

复杂网络在数学上可以描述成一个图G= （V，E），其中V= ｛v1，v2，v3…，vN｝表示节点集合，E= ｛e1，e2，e3，…，eW｝⊆V×V表示边的集合，N=｜V｜表示节点数量，W=｜E｜表示边数量。简单无权图G可以用邻接矩阵A（G）=（aij）M×N表示，其中aii=0，若vi与vj之间存在边则aij=1，否则aij=0。假设G为无向图，则A（G）为对称矩阵，即aij=aij。令λ1≥λN≥…≥λN为A（G）的特征根，称集合｛λi｝为图G的邻接矩阵特征谱。

称图G= （V，E）中节点和边的交替序列w=v0e1v1e2…ekvk为途径，其中vi∈V，ei= （vi-1，vi）∈E，k为途径w的长度，简单图中的途径w可简写为v0v1…vk。若途径w中v0=vk则称w为闭途径。考虑图1中节点v1和v6之间的途径数目。在图1a中，v1和v6之间长度为1和2的途径数目为零；长度为3的途径有4条：v1v2v4v6，v1v3v5v6，v1v2v5v6，v1v3v4v6；长 度 为 4 的 途 径 有 8 条：v1v2v3v5v6，v1v2v4v5v6，v1v3v5v4v6，v1v3v2v4v6，v1v2v5v4v6，v1v3v4v5v6，v1v2v3v4v6，v1v3v2v5v6。在图1b中，v1和v6之间长度为1，2和4的途径数目为零；长度为3的途径有2条：v1v2v4v6，v1v3v5v6。显然，图1 a中v1和v6之间连接的抗毁性更强，因为两个节点之间存在更多的替代途径，当网络中部分节点或者边失效后，v1和v6之间还能继续保持连通。

通过图1的例子可以看出，节点之间连接的抗毁性来源于节点之间替代途径的冗余性。由此可以认为网络的抗毁性来源于网络中替代途径的冗余性。那么，如何度量网络中替代途径的冗余性呢？直观上来说，可以统计任意节点对vi↔vj之间长度为k的途径数目n，然后对i，j，k求和

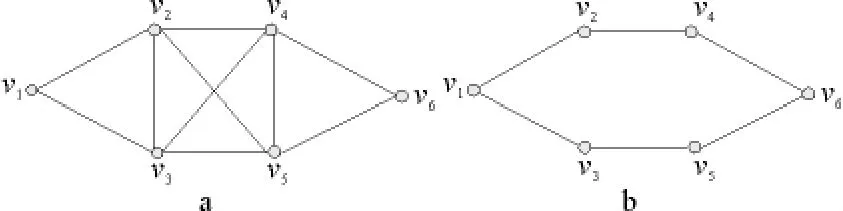
图1 网络中的途径数目示意图Fig.1 Illustration of number of walks

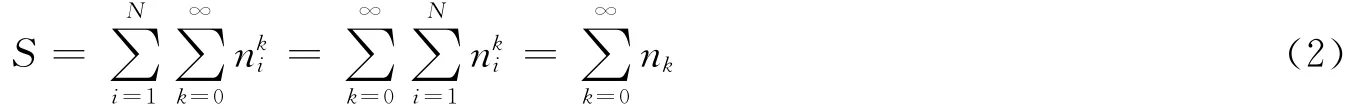
其中，nk表示网络中所有长度为k的闭途径数目。S越大，说明网络中替代路径的冗余性越高，网络的抗毁性就越强。注意到网络中的途径允许节点和边重复，这意味着闭途径的长度可以为任意长度，因此S→∞。为了克服这个问题，考虑对nk进行加权，即

选择这样加权有3方面原因：1）越长的途径被重复计算的次数越多，例如网络中一条边在计算长度为2的闭途径时被重复计算了2次，网络中一个三角形在计算长度为3的闭途径时被重复计算了6次；2）越长的途径对网络抗毁性贡献越小；3）保证S收敛。为了化简式（3），先给出一个引理。

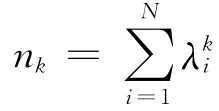
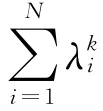
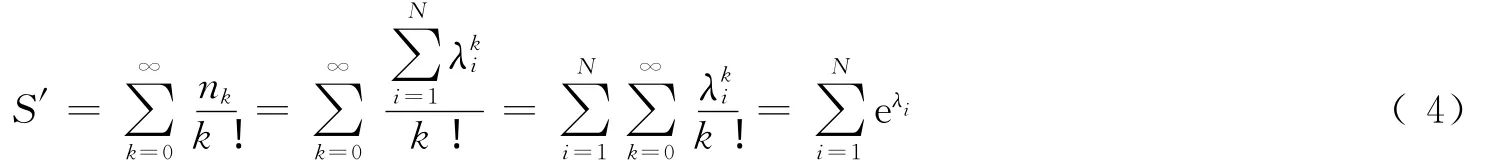
这表明闭途径数目的加权和可通过特征谱直接得到。注意到当N很大时S将是一个庞大的数字，考虑对S重新标度，并记为

定义1 称

为图G的自然连通度，其中λi为图G邻接矩阵A（G）的特征根。

2 基于自然连通度的复杂网络抗毁性组合优化模型

2.1 目标函数

目标函数是优化问题的关键，不同的目标函数将得到不同的优化结果。此外，目标函数也决定了优化的效率。对于大规模复杂网络，如果选择基于图论的抗毁性指标将很难执行优化过程。从定义1可知，自然连通度可以直接从网络邻接矩阵的特征谱导出，在数学形式上表示为一种特殊形式的平均特征根，具有明确的物理意义和简洁的数学形式并且计算简单。此外，自然连通度关于添加边或移除边是严格单调的［20-21］，这意味着自然连通度能够精确刻画网络抗毁性的细微差别。通过与其他抗毁性测度比较，发现自然连通度能够准确、清晰地刻画出复杂网络抗毁性的演化，得到的结果与直观判断相符，而且对于不连通图仍然有效［20-21］。

因此，本文选择既精确又便于计算的自然连通度作为复杂网络抗毁性优化的目标函数。

2.2 约束条件

网络的抗毁性受很多因素的影响，其中最主要的因素是网络中边的数目。由于自然连通度关于添加边是严格单调递增的，这意味着如果没有边的数量限制，完全图将是抗毁性最优的网络。但是，构造一个网络总是有一定成本约束的，边的数量越多网络的成本越大。因此，本文将网络中边的数量作为约束条件，即研究边的数量给定的条件下，如何使得网络的抗毁性最优。边的数量约束可以通过邻接矩阵表示

2.3 优化模型

根据前面讨论的目标函数以及约束条件，可以得到复杂网络抗毁性优化模型为

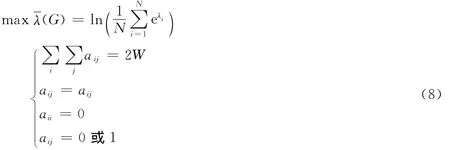
显然，这是一个典型的组合优化问题。

3 基于禁忌搜索的复杂网络抗毁性仿真优化算法

考虑到现代启发式方法是解决复杂组合优化问题的有效工具，本文采用现代启发式方法中的新成员——禁忌搜索（Tabu Search，TS）算法［26-27］来求解式（8）所描述的组合优化模型。禁忌搜索是局部领域搜索的一种扩展，通过局部邻域搜索机制和相应的禁忌准则来避免迂回搜索，并通过特赦准则来赦免一些被禁忌的优良解，进而保证多样化的有效探索以最终实现全局优化。

3.1 变量编码

由式（8）中的约束条件可知，只需要优化邻接矩阵中对角线以上的N（N-1）/2个元素aij（i＜j）。把这N（N-1）/2个元素重新排列，记为xi，其中xi=0或xi=1，∑ixi=W。将xi作为禁忌搜索算法的优化变量，即解的编码。

3.2 移动操作

禁忌搜索是局部邻域搜索的一种扩展，因此解的移动操作设计非常关键，它决定了当前解邻域的产生形式和数目以及各个解之间的联系。本文选择边随机重连作为移动操作，其算法为：

Step 1随机移除一条边，即在xi中随机选择一个等于1的变量令其等于0；

Step 2随机添加一条边，即在xi中随机选择一个等于0的变量令其等于1。

对于每一个当前解，通过边随机重连产生ncandidate个新网络作为当前解的候选解集。

3.3 特赦准则

特赦准则设置是算法避免遗失优良解，激励对优良解的局部搜索，进而实现全局优化的关键步骤。在禁忌搜索过程中，可能会出现一个被禁忌候选解的目标函数优于当前解，此时解禁该禁忌候选解，以实现更高的优化性能。

3.4 终止准则

通常终止准则选择为是否达到预定的最大迭代次数，而这种预定的最大迭代次数一般是根据经验确定。显然，迭代次数的多少应与寻优问题规模有关。凭经验给定最大迭代次数可能会产生两类问题：1）优化过程早己达到最优解，但是没有达到最大迭代次数，优化过程还要做不必要的迭代计算；2）优化过程己经达到最大迭代次数，但尚未达到最优解就退出优化过程。为了克服上述问题，采用最优解连续保持不变是否达到最大持续迭代步数niteration作为终止准则。

3.5 算法流程

具体的基于禁忌搜索的复杂网络抗毁性仿真优化算法：

Step 1初始化算法：设置禁忌表长度L、候选解集规模ncandidate以及最大持续迭代步数niteration；置禁忌表为空。

Step 2产生初始解G0：先置xi：=0，然后从中随机选取W 个变量置其等于1；置最优解G＊：=G0，置当前解Gnow：=G0；

Step 3判断终止准则是否满足，若是，则结束算法并输出优化结果；否则，继续以下步骤。

Step 4生成候选解集：通过边随机重连产生ncandidate个新网络，若产生的新网络不连通，则重新选择；计算每个新网络的自然连通度。

Step 5如果自然连通度最大的候选解不是被禁忌的，或者被禁忌的但满足特ncandidate=10赦准则，那么就把该候选解作为新的当前解Gnow；否则，选择不被禁忌的最好移动所对应的候选解作为当前解Gnow，并将该候选解加入禁忌表；如果当前解Gnow的自然连通度大于最优解，则置最优解G＊：=Gnow。

Step 6转Step 3。

4 仿真分析结果

基于本文的禁忌搜索仿真优化算法分析优化过程以及最优抗毁性网络的各种结构属性。仿真优化参数为：节点数量N=100，边的数量W=300，禁忌表长度L=10、候选解集规模以及最大持续迭代步数niteration=30。

4.1 自然连通度

图2给出了自然连通度随迭代次数n的变化图。

由图2可见，自然连通度随着迭代次数的增加而快速增加，从初始值2.84经过582次迭代后达到稳定最优值11.05。这说明本文提出的基于禁忌搜索的复杂网络抗毁性仿真优化算法能有效地优化复杂网络的抗毁性。作为参考，在图2中还给出了具有相同节点数量以及边数量的BA无标度网络（实线）、规则环状格子（虚线）、ER随机网络（点划线）的自然连通度。可以看出，通过优化得到的网络抗毁性远远高于这些典型网络。

4.2 度关联性

度关联性刻画的是网络中不同度节点之间的微观连接模式。如果度大的节点倾向于连接度大的节点，则称网络是同配的；反之，如果度大的节点倾向于和度小的节点连接，则称网络是异配的。度关联性可用节点度的Pearson相关系数描述［28］。

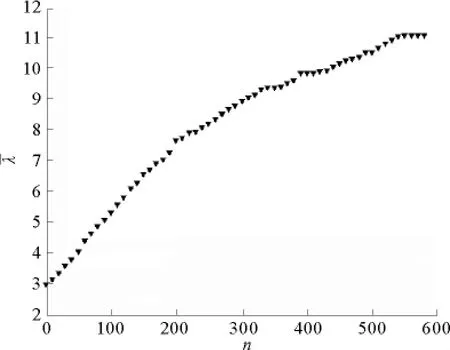
图2 自然连通度随迭代次数变化图Fig.2 The change of natural connectivity with the number of iterations

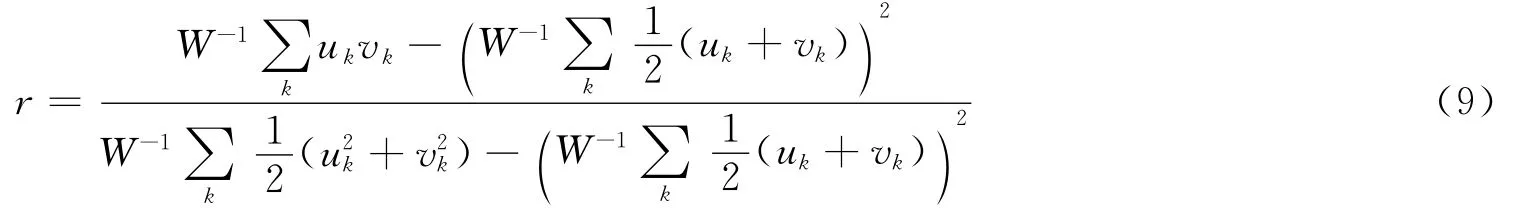
其中，uk、vk分别为连接第k条边的两个节点的度，W 为网络的总边数。r的取值范围为-1≤r≤1，当r＞0时，网络是同配的；当r＜0时，网络是异配的；当r=0时，网络是不相关的。

图3给出了度关联系数随迭代次数n的变化图。可以看出，度关联系数随着迭代次数的增加呈震荡上升趋势，最优网络的度关联系数达到0.25，呈现出明显的同配关联模式，即度大的核心节点倾向于和度大的核心节点相连接，度小的末梢节点倾向于和度小的末梢节点相连接。作为参考，在图3中给出了具有相同节点数量以及边数量的BA无标度网络（实线）、规则环状格子（虚线）、ER随机网络（点划线）的度关联系数。可以看出，BA无标度网络呈现出明显的异配关联模式，规则环状格子和随机网络的度关联系数接近0，即不存在明显的度关联，通过优化得到的度关联系数明显高于这些典型网络。

4.3 拓扑结构图

为了直观展现最优抗毁性网络的结构属性，在图4中给出了最优抗毁性网络的拓扑结构图（图4a）。作为参考，在图4中还给出了具有相同节点数量以及边数量的BA无标度网络（图4b）、规则环状格子（图4 c）、ER随机网络（图4d）的拓扑结构图。可以看出，最优抗毁性网络的拓扑结构图与其他几个典型网络有很大不同。在最优抗毁性网络中存在少量度非常大的核心节点，而且这些核心节点之间相互连接紧密形成“富人俱乐部”。除了这些核心节点以外，其他节点的度都很小，而且这些度很小的末梢节点倾向于在外围互相连接。

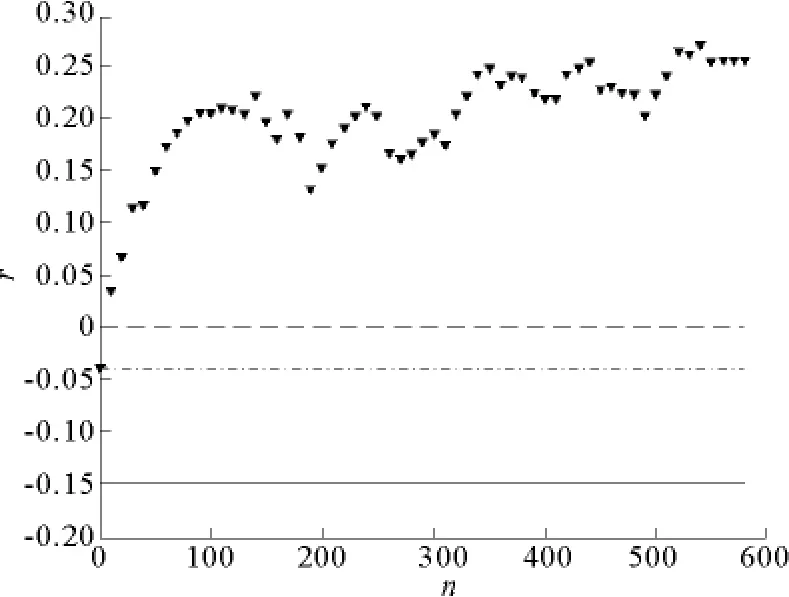
图3 度关联系数随迭代次数变化图Fig.3 The change of degree correlation coefficient with the number of iterations

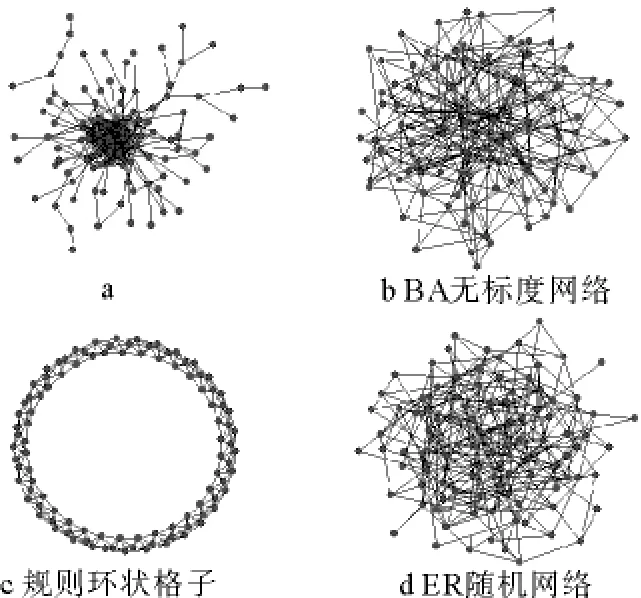
图4 最优抗毁性网络的拓扑结构Fig.4 The network topology with optimal invulaer-ability

5 结束语

本文围绕“怎样得到抗毁性好的复杂网络”研究了复杂网络抗毁性的仿真优化问题，主要工作包括：1）建立了以自然连通度为目标函数，以边的数量为约束条件的复杂网络抗毁性组合优化模型；2）提出了基于禁忌搜索的复杂网络抗毁性仿真优化算法，设计了变量编码、定义了移动操作、给出了特赦准则、设置了终止准则，给出了算法流程；3）分析了最优抗毁性网络的若干结构属性，研究表明最优抗毁性网络呈现出明显的同配度关联模式，核心节点之间相互连接紧密形成“富人俱乐部”，度很小的末梢节点倾向于在外围互相连接。

值得指出的是，本文研究的是复杂网络抗毁性的全局优化问题，即在一定费用约束条件下如何构造出抗毁性更好的网络。但是，很多情况下面对的都是已经存在的网络。这意味着不可能全部“重新洗牌”，只能局部优化网络结构。在这种情况下，如何通过最少的优化达到最大的抗毁性是我们下一步需要研究的问题。

［1］方锦清，汪小帆，刘曾荣.略论复杂性问题和非线性复杂网络系统的研究［J］.科技导报，2004，22（2）：9-12，64.

Fang Jinqing，Wang Xiaofan，Liu Zengrong.On the study of complexity and nonlinear complex networks［J］.Science &Technology Review，2004，22（2）：9-12，64.

［2］方锦清，汪小帆，郑志刚，等.一门崭新的交叉科学：网络科学（上）［J］.物理学进展，2007，27（3）：239-343.

Fang Jinqing，Wang Xiaofan，Zheng Zhigang，et al.New interdisciplinary science：networks science（I）［J］.Progress in Physics，2007，27（3）：239-343.

［3］方锦清，汪小帆，郑志刚，等.一门崭新的交叉科学：网络科学（下）［J］.物理学进展，2007，27（4）：361-448.

Fang Jinqing，Wang Xiaofan，Zheng Zhigang，et al.New interdisciplinary science：networks science（I）［J］.Progress in Physics，2007，27（4）：361-448.

［4］陈禹.人类对于网络的认识的新发展［J］.系统辩证学报，2005，13（4）：18-22.

Chen Yu.New progress on the network for the human being［J］.Journal of systemic dialectics，13（4）：18-22.

［5］史定华.网络——探索复杂性的新途径［J］.系统工程学报，2005，20（2）：115-119.

Shi Dinghua.Networks—a new approach for exploring complexity［J］.Journal of System Engineering，2005，20（2）：115-119.

［6］汪秉宏，周涛，何大韧.统计物理学与复杂系统研究最新发展趋势分析［J］.中国基础科学，2005，7（3）：37-43

Wang Binghong，Zhou Tao，He Daren.The trend of recent research on statistical physics and complex systems［J］.China Basic Science，2005，7（3）：37-43.

［7］汪小帆，李翔，陈关荣.复杂网络理论及其应用［M］.北京：清华大学出版社，2006.

［8］谭跃进，吴俊，邓宏钟.复杂网络抗毁性研究综述［J］.系统工程，2006，24（11）：1-5.

Tan Yuejin，Wu Jun，Deng Hongzhong.Invulnerability of complex networks：a survey［J］.System Engineering，2006，24（11）：1-5.

［9］吴俊，谭跃进.复杂网络抗毁性测度研究［J］.系统工程学报，2005，20（2）：128-131.

Wu Jun，Tan Yuejin.Study on measure of complex network invulnerability［J］.Journal of System Engineering，2005，20（2）：128-131.

［10］谭跃进，吕欣，吴俊，等.复杂网络抗毁性研究若干问题的思考［J］.系统工程理论与实践，2008，28（Suppl）：116-120.

Tan Yuejin，LüXin，Wu Jun，et al.On the invulnerability research of complex networks［J］.Systems Engineering-Theory &Practice，2008，28（Suppl）：116-120.

［11］Frank H，Frisch I T.Analysis and design of survivable network［J］.IEEE Transaction on Communication Technology，1970，COM-18（5）：567-662.

［12］Chvatal V.Tough graphs and hamiltonian circuits［J］.Discrete Mathematics，1973，5（3）：215-228.

［13］Barefoot C A，Entringer R，Swart H.Vulnerability in graphs-a comparative survey［J］.J Combin Math Combin Comput，1987，1（2）：13-22.

［14］Cozzens M，Moazzami D，Stueckle S.The tonaeity of a graph［C］//Seventh International Conference on the Theory and Applications of Graphs.New York：Wiley，1995：1111-1122.

［15］Jung H A.On a class of posets and the corresponding comparability graphs［J］.J Combin Theory B，1978，24（2）：125-133.

［16］Bassalygo L A，Pinsker M S.The complexity of an optimal non-blocking commutation scheme without reorganization［J］.Problemy Peredaci Informacii，1973，9（1）：84-87.

［17］许进.系统的核与核度理论Ⅱ——优化设计与可靠通讯网络［J］.系统工程学报，1994，9（1）：1-11.

Xu Jin.The core and coritivity of a system Ⅱ—optimization design and reliable communication network［J］.Journal of System Engineering，1994，9（1）：1-11.

［18］许进，席酉民.系统的核与核度［J］.系统科学与数学，1993，13（2）：102-110.

Xu Jin，Xi YouMin.The core and coritivity of a system［J］.System and Mathematics，1993，13（2）：102-110.

［19］Kratsch D.Measuring the vulnerability for classes of intersection graphs［J］.Discr App Math，1997，77（3）：259-270.

［20］Wu J，Barahona M，Tan Y J，Deng H Z.Natural connectivity of complex networks［J］.Chinese Physics Letters，2010，27（7）：078902.

［21］Wu J，Barahona M，Tan Y J，et al.Spectral measure of structural robustness in complex networks［J］.Ieee Transactions on Systems Man and Cybernetics Part A-Systems and Humans，2011，41（6）：1244-1252.

［22］Estrada E，Hatano N，Benzi M.The physics of communicability in complex networks［J］.Phys Rep，2012，514（3）：89-119.

［23］Shang Y L.Perturbation results for the Estrada index in weighted networks［J］.Journal of Physics，2011，44（7）：075003.

［24］Shang Y L.Local natural connectivity in complex networks［J］.Chinese Physics Letters，2011，28（6）：068903.

［25］Cvetkovic′D M，Doob M，Sachs H.Spectra of Graphs［M］.New York：Academic Press，1979.

［26］Glover F.Tabu Search-Part II［J］.ORSA Journal on Computing，1990，2（1）：4-32.

［27］Glover F.Tabu Search-Part I［J］.ORSA Journal on Computing，1989，1（3）：190-206.

［28］Newman M E J.Assortative mixing in networks［J］.Physical Review Letters，2002，89（20）：20871.

Simulation Optimization for Invulnerability of Complex Networks Based on Natural Connectivity

TIAN Tian1，WU Jun2，TAN Yue-jin2
（1.POL Research Institute of General Logistics Pepartment，PLA，Beijing 102300，China；2.College of Information Systems and Management，National University of Defense Technology，Changsha 410073，China）

A combinatorial optimization model for invulnerability of complex networks is established，in which the natural connectivity is the objective function and the number of edges is the constraint condition.Following the combinatorial optimization model，a simulation optimization method for invulnerability of complex network topologies based on tabu search is proposed and variables coding，moving operation，aspiration criterion，stopping criterion，algorithm procedures are provided.Lastly，the structural properties of the optimal network topology are investigated based on the simulation results.The results show that the optimal networks with invulnerability have obvious homogenous correlation.Tight connection exists among hub nodes and forms“rich club”.

complex networks；invulnerability；natural connectivity；tabu search；simulation optimization

N949

A

1672-3813（2013）02-0088-07

2013-03-14

国家自然科学基金（60904065，71031007，71171195）；新世纪优秀人才支持计划（NCET-12-0141）

田田（1979-），男，黑龙江哈尔滨人，硕士，工程师，主要研究方向为计算机工程。

（责任编辑 耿金花）