随机地震激励作用下水中悬浮隧道锚索的动力响应
董满生, 赵佳佳, 牛忠荣, 耿淑伟
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009;2.合肥工业大学 交通运输工程学院,安徽 合肥 230009;3.上海交通大学 海洋工程国家重点实验室,上海 200240)
0 引 言
水中悬浮隧道(Submerged Floating Tunnel,简称SFT)又称阿基米德桥,是一种悬浮在水面下方的通道,对于那些由于环境限制使得水域难以跨越的地方,悬浮隧道提供了跨越的可能性。通常悬浮隧道自身重力小于浮力,通过锚索平衡富余浮力以达到平衡。与地面结构物所处环境不同,水中悬浮隧道除了承受自重和车辆载荷外,还受到浮力、波浪、海流及地震等各种环境动力荷载的作用,而维持悬浮隧道的稳定主要依靠锚索的作用,因此研究锚索在复杂环境作用下的动力响应,成为研究悬浮隧道安全性、稳定性的重点。
文献[1]对水流下悬浮隧道的动力响应进行研究,比较了涡激振动和参数振动对锚索振幅的影响;文献[2]对悬浮隧道在波流联合作用下的动力响应进行了研究,通过数值计算得出悬浮隧道的放置深度、跨越长度、隧道断面形式和支撑形式对悬浮隧道静、动态响应的影响;文献[3]对地震和水流作用下悬浮隧道整体结构动力响应进行三维数值模拟;文献[4]针对北海道的波浪环境,进行了SFT的动态特性二维模型试验;文献[5]分析了风浪作用下SFT的动态响应,用基于Navier-Stokes方程的有限元方法计算了规则波作用下二维模型的水动力;文献[6]提出了波浪和地震等环境载荷下SFT的工程分析程序。锚索作为悬浮隧道关键机构之一,成为悬浮隧道研究的一个热点,已有一些研究关注波、流或波流联合作用所致的涡激振动[7-9],但关于地震作用下锚索的动力行为的相关报道不多,因此深入了解锚索对地震激励的动力反应对悬浮隧道结构设计和理论研究至关重要。
本文考虑锚索振动时水体的流固耦合作用,建立锚索非线性动力方程,运用虚拟激励法结合数值软件研究锚索的随机地震反应,得出地震作用下悬浮隧道锚索的速度和位移动力响应,用以评价水中悬浮隧道在随机地震激励下的动力学行为。
1 地震作用下悬浮隧道锚索振动分析
根据水中悬浮隧道的水下定位方式,其结构形式通常可分为锚索式悬浮隧道、浮筒式悬浮隧道和固定支撑式悬浮隧道。本文的研究对象为锚索式悬浮隧道,其结构系统主要由管体、锚索和锚固桩等结构组成,结构示意图如图1所示。
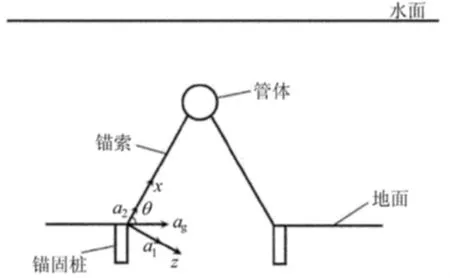
图1 悬浮隧道结构示意图
为了简化地震作用下水中悬浮隧道锚索模型,本文作以下假设:
(1)悬浮隧道锚索所受的拉力远大于其自身重力,拉力沿长度方向不变。
(2)锚索几何尺寸和材料性质沿长度方向不变。
(3)锚索的抗弯刚度很小,忽略不计。
(4)地震作用下由锚固桩处以水平剪切波形式输入。
系统坐标系如图1所示,坐标原点设在锚索底端。锚索具有一定的垂度而不处于绷直的状态,采用等效弹性模量方法考虑锚索的垂度效果,即将具有较高初始应力和一定垂度的锚索等效为一直弦杆。采用Morison公式考虑结构运动所产生的水动力。根据以上假设,运用达朗贝尔原理可得地震作用下锚索横向振动微分方程为:

其中,Eeq为考虑锚索垂度效应后的锚索等效弹性模量[10],Eeq=E/(1+E/Ef),E 为锚索的弹性模量,Ef=(Lcosθ)2,Ef为锚索垂度产生的模量;σ=T0/A为锚索应力,T0为锚索静力平衡时的张力,A为锚索横截面积;γ1为锚索的浮容重;L为锚索长度;θ为锚索倾角;ε为锚索的动应变;c为锚索的黏滞阻尼系数;m为单位长度锚索的质量;FD为锚索横向振动时水体对其单位长度的水动力;ag为地震波加速度。
锚索的动应变可由泰勒公式写为:
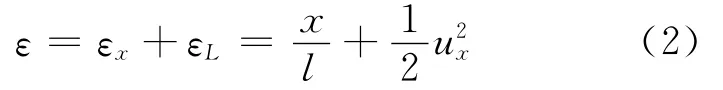
由Morison公式可知,锚索振动时水体对其单位长度的作用力可写成附加惯性力和阻尼力之和[11],即
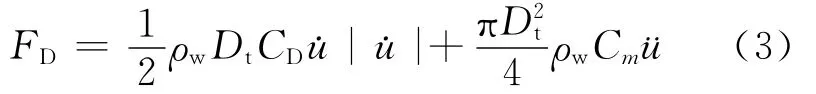
其中,ρw为水体密度;Dt为锚索直径;CD为拖曳力系数,取CD=0.7;Cm为附加质量系数,取Cm=1。
地震加速度ag由反应谱[12]可得。平稳随机地面加速度ag的谱密度Sa(ω)已给定,则虚拟简谐地面激励[13]为:

令magcosθ=F1,magsinθ=F2,方程(1)可写为:


锚索两端为铰接,采用分离变量法,则振动位移[14]可写为:
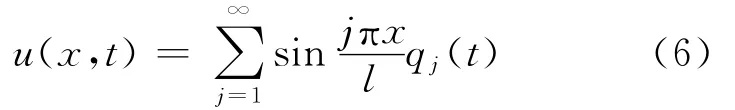
将(2)式、(3)式和(6)式代入(5)式得:
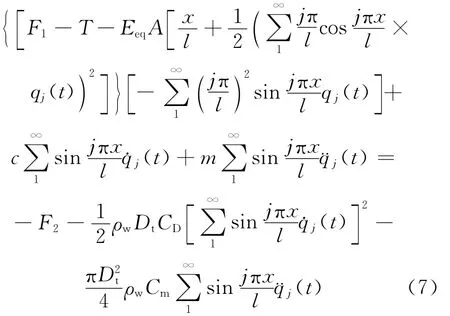
文献[15]指出,张紧弦的端部激励振动的基本模态占主要地位,取一阶振动模态简化(7)式,整理得:
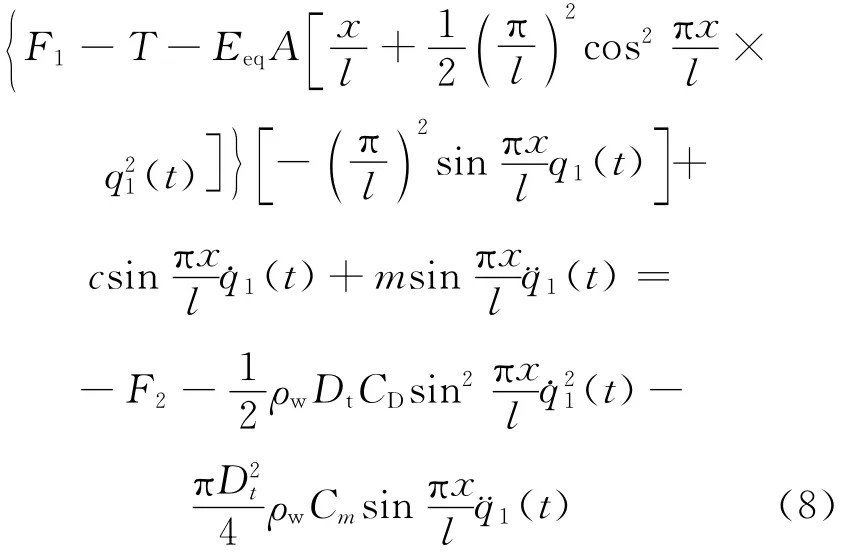
(8)式两端各项乘以φ(x)=sin(πx/l),沿梁长度方向积分,并考虑正交条件得:

(9)式可写为:
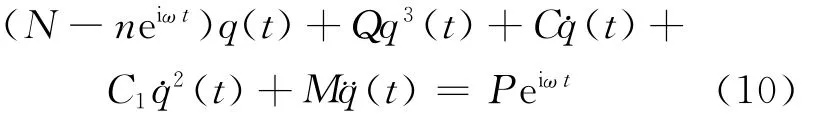
分析可得N≫n,故可以忽略轴向力对锚索的影响,(10)式可简化:
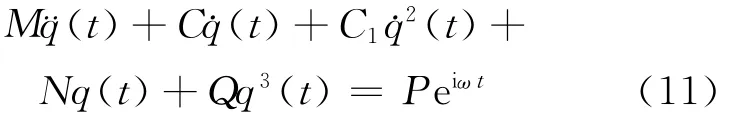
(11)式为非线性方程,可见地震下锚索动力响应属于非线性问题。为解决此问题本文采用非线性问题等效线性化[13]的方法进行求解,即用一个有精确解的线性系统代替非线性系统,并使得两方程之差在统计意义上为最小。对高阶项系数进行求导,与一阶项进行合并,通过迭代的方法求解出非线性项的等效线性系数,等效方程为:
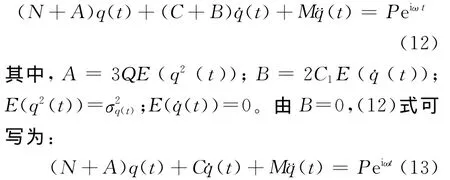
取初始值E(q2(t))=1,代入(13)式,通过数值软件迭代计算,当 An-An+1<An+1/100,则取迭代完成,通过迭代法可求出A=102.0922。
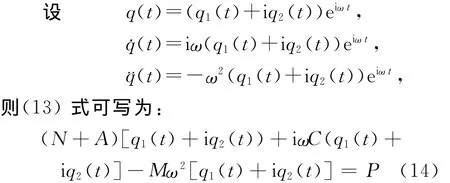
(14)式两边实部、虚部分别相等,可解得:
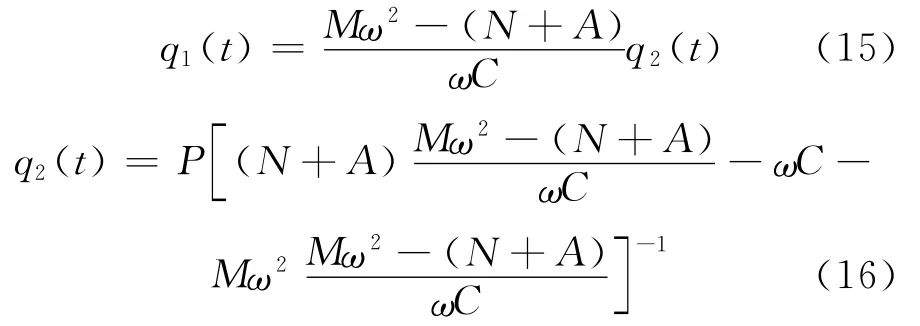
2 平稳随机振动数值模拟
数值模拟悬浮隧道结构参数见文献[10]。地面加速度自功率谱采用Kanai-Tajimi平稳过滤白噪声公式[16],即
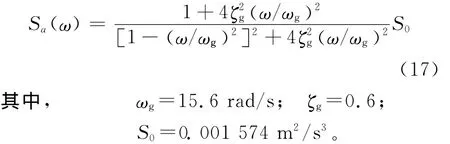
白噪声功率谱如图2所示。锚索中间位置响应最为剧烈,取锚索x=l/2位置位移功率谱密度函数为:
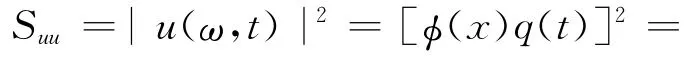
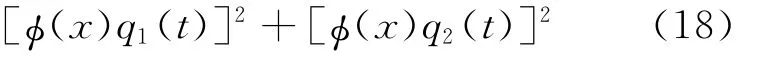
运用Matlab数学软件分别对其展开式功率谱进行仿真,仿真结果如图3、图4所示。
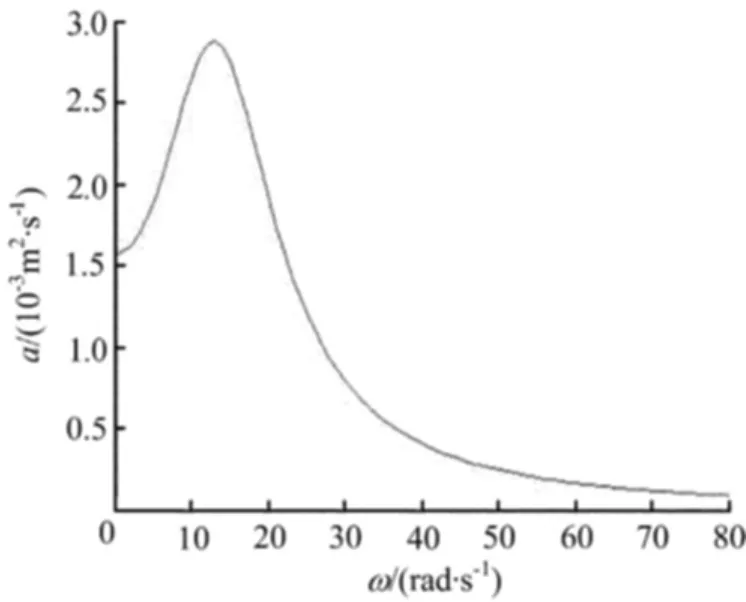
图2 白噪声功率谱
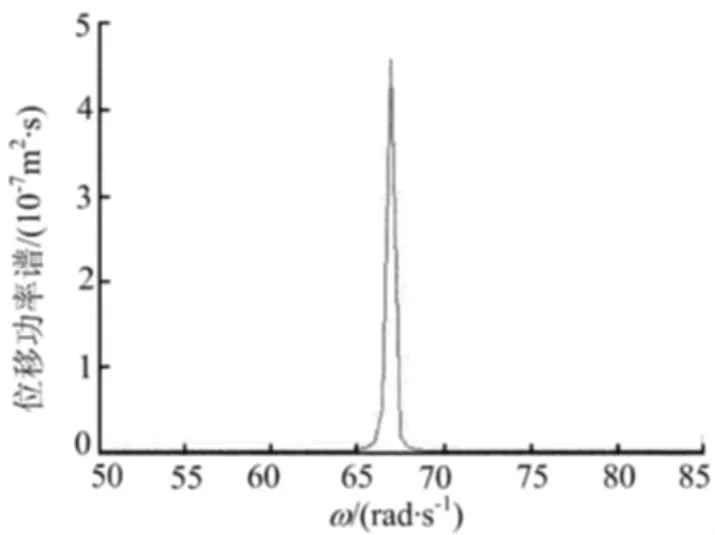
图3 位移功率谱密度曲线
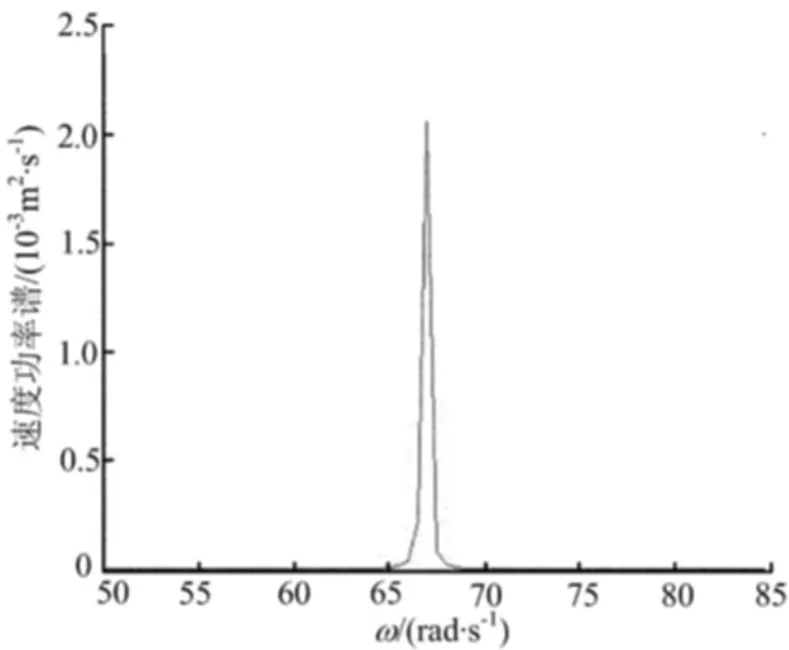
图4 速度功率谱密度曲线
从图3、图4可以看出,平稳随机地震作用下悬浮隧道锚索中间位置位移响应和速度响应均在角频率为67rad/s左右达到最大,其最大值分别为4.9×10-7m2·s和2.1×10-3m2/s。
3 非平稳随机振动数值模拟
结构受地震、阵风之类的随机作用有时持续时间很短,以至于激励的平稳性假定不成立,结构的非平稳随机[17]响应得到研究。对于非平稳随机过程,已有多种功率谱模型,其中演变功率谱密度模型在地震中得到广泛应用,具体形式为:

对于非平稳随机过程,假定非均匀调制函数A(ω,t)和对应的零均值平稳地面加速度¨xg(t)的谱密度Sa(ω)已知,则虚拟简谐地面激励为:

计算过程与平稳类似计算中调制函数的选取取决于地面运动的持续时间,A(ω,t)的表达式为:
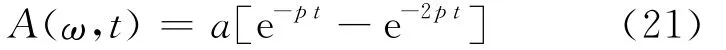
计算中,p=0.0995,调制函数如图5所示。
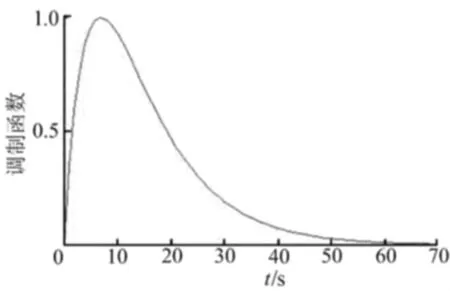
图5 调制函数曲线
此时功率谱函数为随时间变化的函数,即
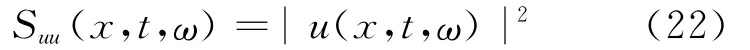
锚索中间位移功率谱密度函数为:
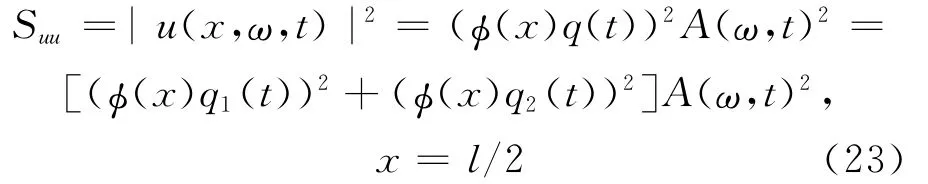
经过计算和Matlab仿真所得结果如图6所示。
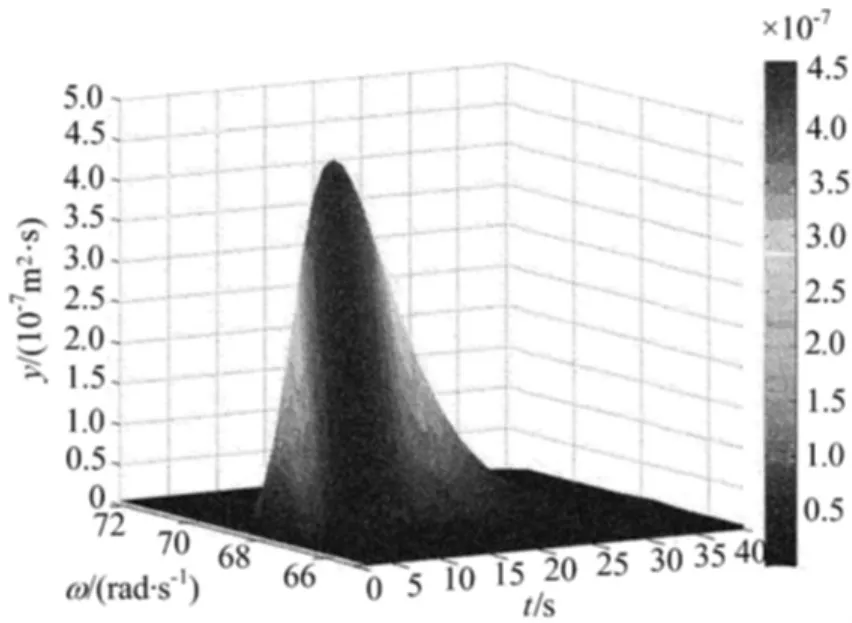
图6 非平稳位移功率谱曲线
从图6可以看出,非平稳随机振动锚索中间处位移响应在角频率为67rad/s、时间为10s左右达到最大,其值为4.4×10-7m2·s。
4 结束语
本文考虑了流固相互作用,将锚索简化为受张力的弦,对地震锚索动力方程的非线性项进行等效线性化处理,采用虚拟激励法研究地震作用下悬浮隧道锚索的动力响应,给出该类结构的一种理论分析方法。研究结果表明,地震输入轴向力对锚索的横向振动影响较小,可忽略;锚索振动时水的附加阻尼力与附加惯性力相比较小,影响可忽略。
[1]陈建云,孙胜男,王变革.水下悬浮隧道锚索的动力响应分析[J].计算力学学报,2008,25(4):488-493.
[2]麦继婷,杨显成,关宝树.悬浮隧道在波流作用下的响应分析[J].铁道学报,2008,30(2):118-123.
[3]Di Pilato M,Perotti F,Fogazzi P.3Ddynamic response of submerged floating tunnels under seismic and hydrodynamic excitation[J].Engineering Structures,2008,30:268-281.
[4]Kunisu H,Mizuno S,Mizuno Y,et al.Study on submerged floating tunnel characteristics under the wave condition[C]//ISOPE Proceedings of the International Offshore and Polar Engineering Conference,1994:27-32.
[5]Remseth S,Leira B,Okstad K,et al.Dynamic response and fluid/structure interact ion of submerged floating tunnels[J].Computers and Structures,1999,72(3):659-687.
[6]Brancaleoni F,Castellani A,Dasdia P.The response of submerged tunnels to their environment[J].Engineering Structures,1989,11(1):48-62.
[7]葛 斐,龙 旭,王 雷,等.水中悬浮隧道管段锚索耦合模型涡激震动研究[J].中国公路学报,2009,22(3):83-100.
[8]陈建云,王变革,孙胜男.悬浮隧道锚索的涡激动力响应分析[J].工程力学,2007,24(10):186-192.
[9]陈建云,孙胜男,苏志彬.水流作用下悬浮隧道锚索的动力响应[J].工程力学,2008,25(10):229-234.
[10]孙胜男.悬浮隧道动力响应分析[D].辽宁大连:大连理工大学,2008.
[11]竺艳蓉.海洋工程波浪力学[M].天津:天津大学出版社,1991:70-95.
[12]高玉峰,张 建.地震危险性分析研究[M].北京:科学出版社,2007:110-145.
[13]林家浩,张亚辉.随机振动的虚拟激励法[M].北京:科学出版社,2004:150-200.
[14]唐友刚.高等结构动力学[M].天津:天津大学出版社,2002:40-80.
[15]Tagata G.Garmonically forced finit amplitude vibration of a string[J].Journal of Sound and Vibration,1977,51(4):483-492.
[16]韩晓双.导管架海洋平台地震响应研究[D].辽宁大连:大连理工大学,2008.
[17]王建国,李雪峰 .斜拉桥地震响应振动控制Benchmark问题研究[J].合肥工业大学学报:自然科学版,2008,31(6):932-936.

