镜头孔径光阑与透视中心关系分析

史艳琼， 卢荣胜， 陈 琳

（合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009）

0 引 言

相机成像过程是把三维空间物体上的点通过镜头透视关系映射到传感器像平面上的二维空间，这种映射常常用薄透镜小孔模型近似，即把镜头简化抽象成一个薄透镜，空间点与像平面上的对应点的连线交于透镜中心一点，该点即为透视中心［1］。这种简化透视变换模型能够满足大多数固定焦距成像的机器视觉应用场合，因为在这些场合并不需要知道镜头的透视中心在镜头上的真实物理位置，但是这种近似在有些场合是不可以的。如在全景成像时，需要知道相机透视中心的准确位置，让相机围绕透视中心旋转，拍摄多幅图像，保证在不同转角处获得的序列图像透视中心在同一个位置，才能比较容易地采用图像拼接技术获得更大画幅的全景图像。

在视觉跟踪领域，为了获得较高的影像分辨率以及保持跟踪图像大小不变，常常使用方位角、俯仰角和倍率的PTZ（Pan－Tilt－Zoom，简 称PTZ）相机［2－3］。另外在大空间三维测量时，也用到多个PTZ相机进行跟踪［4－5］，该相机也需要绕着水平和垂直轴旋转。在理想的情况下，水平轴和垂直轴的交点应该与相机的透视中心重合，这样会大大减小视觉建模的难度。但是，相机镜头是由多个镜组组成，并非能够用薄透镜进行精确等效。在利用PTZ相机成像时，当镜头的倍率发生变化时，透视中心的位置也会发生变化。如何确定镜头的透视中心位置，一直是人们争论的话题。有人认为旋转中心在镜头的节点附近，有人认为在入瞳附近。

本文就这一问题展开分析，并进行实验验证，为了证明实际镜头的透视中心与镜头的孔径光阑（入瞳）有关，首先从透镜的光线追迹、成像规律及孔径光阑对成像的影响入手，分析镜头的透视中心的位置。

1 透镜成像规律与光线追迹

对于薄透镜成像，高斯光学镜头光线追迹遵从以下3条规则［6－7］：

（1）平行于光轴的入射光线，经过透镜折射后，通过光轴上的一个唯一点（即焦点），该点与镜面相距1个焦距的长度。

（2）所有经过镜头中心的入射光线，折射后不改变方向。

（3）从物体上一点发射的光线，不论它从镜头上什么位置入射，折射后都通过一个唯一的像点。

如图1所示，用2个箭头表示物体位置，镜头右边的传感器像平面用IP表示，右边的箭头表示像正好落在传感器像平面上，左边靠近镜头的箭头表示物体的像离焦。

图1a展现了符合规则1和规则2的一个最简单的光线传播情况。

一旦水平和过中心的光线位置确定以后，任何其他光线的传播路径，根据规则3就很容易分析出来，如图1b所示。

但是，真正的透镜是有厚度的，当透镜厚度与透镜焦距相比，对成像的影响不能忽略时，或者透镜是由多片镜组组成，就不能用薄透镜模型进行近似。如图2所示，厚透镜是指有2个折射面，且被分开一段距离的透镜。厚透镜在光轴上有6个基点，在基点处与轴垂直的平面叫基平面，这6个基点分别为物方焦距F、像方焦距F′、物方主点H、像方主点H′、物方节点N及像方节点N′［8］，这6个基点和基平面能够清晰地表达厚透镜的高斯成像特性。

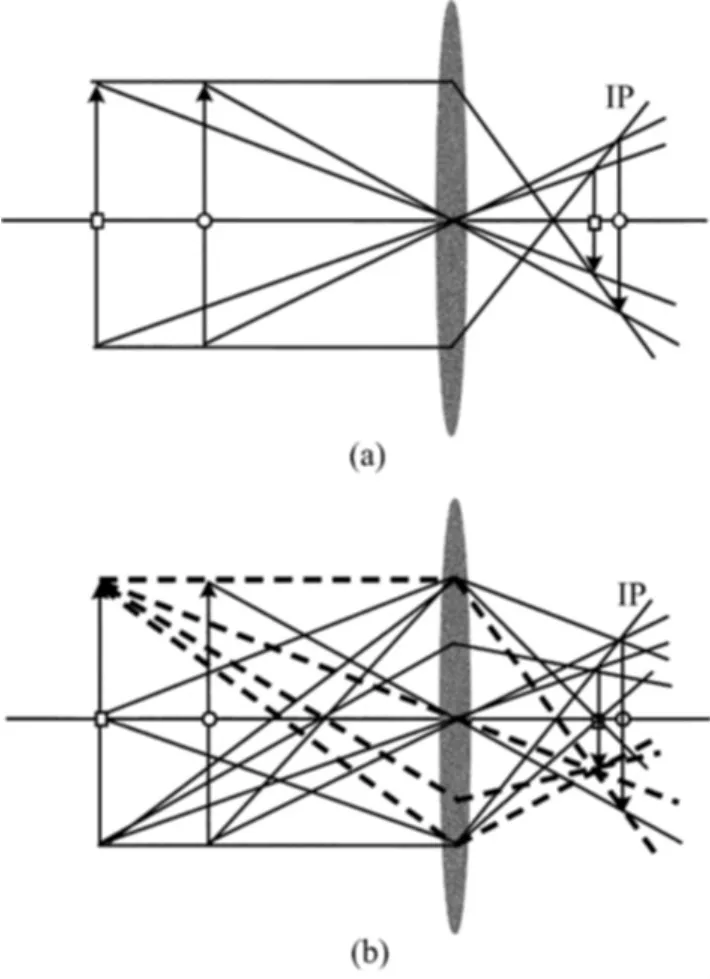
图1 薄透镜高斯光线传播规律

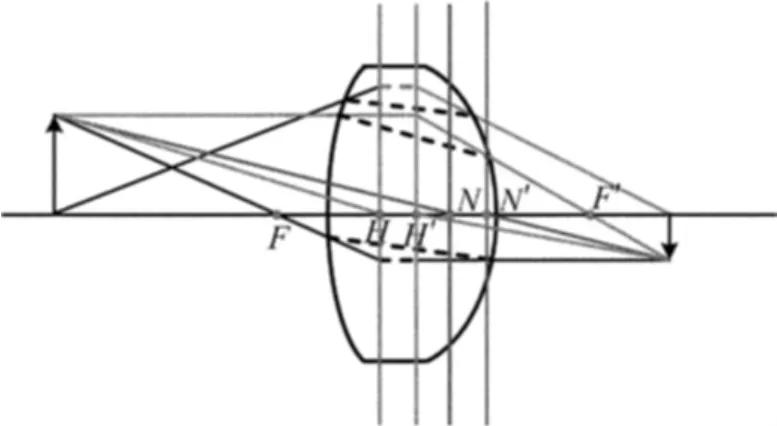
图2 厚透镜的6个基点

对于多个镜片组成的大多数镜头，都可以用厚透镜模型很好地近似，用薄透镜光束追踪的原理追踪厚透镜的几何光束，但是具有比薄透镜更多的参数，薄透镜只有1个参数焦距，但厚透镜有6个参数。在有些情况下，有些参数可能是冗余的。如透镜在均匀介质空气中，前后焦距相同，节点与主点重合，目前使用的传统相机都是这种情况，但是对于油浸式显微镜物镜，情况就不同了。对于在空气中的厚透镜有3个独立参数，即1个焦距和2个焦点。根据这个特性，镜头的2节点和主点很容易确定。在厚透镜的光线追迹过程中，一般任意光线的追迹是比较复杂的。

（1）平行于光轴通过主平面的光线，将不改变方向穿过该主平面，到达另一个主平面，然后折射通过该主平面的焦点。

（2）所有射入节点的光线将从另一节点按原方向射出。

（3）从物体上一点发出的光线，不论从哪个方向射向透镜，最终都折射通过像方一点（像点）［1，7］。

根据前面3条规则，镜头光线追迹如图3所示。虽然在有些情况下使镜头的光学性能分析变得简单明了，但是也给人带来错觉，感觉镜头的透视中心落在镜头的节点上，而产生这种错觉的原因是没有考虑镜头光阑对成像规律的影响。

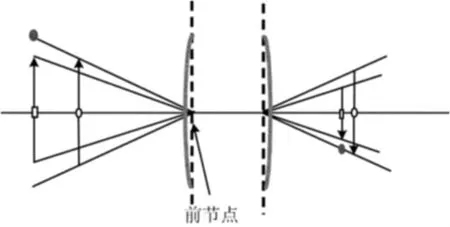
图3 光学通过节点时的传播规律

2 孔径光阑对成像规律的影响

在图1中，虚线表示的光束是能够通过镜头的最大光束，但是如果在光路上插入孔径光阑，则通过透镜的光束大小与位置就要受到光阑的孔径限制。对于物体上正好处于物方焦平面上的那些点，像正好落在传感器像平面上，光束的大小与位置对成像点的位置影响并不大，只是影响光点的亮度。但是对于那些离焦不能正好成像在传感器像平面的物点，光束的大小和位置将是非常重要的因素，它会在传感器像平面上产生图像模糊现象。当光阑孔径越大时，模糊现象越严重。当有些光线被光阑阻挡掉时，模糊会减小。如果被阻挡后剩余的光线足够小，离焦的光点可能变得非常锐利，但是点的位置可能随着被阻挡的光线不同而变化。

2.1 小孔光阑在薄透镜平面上变化的成像规律

首先讨论小孔光阑在理想薄透镜平面上的位置变化对成像规律的影响，如图4所示，图中白色圆圈表示小孔光阑的位置和大小，只有通过光阑孔径的光线才能在图像传感器像平面上成像。左边箭头物体在右边像面上像的位置由主光线与像面的交点确定，主光线是从物体上一点发出通过光阑中心点的光线，物点和像点对光阑孔径的张角决定了像点弥散斑的形状。由于图4中的光阑是小孔光阑，离焦箭头在像面上只产生轻微的模糊影像，图中用灰色像表示。

由图4a～图4c可以看出，当光阑在透镜平面上移动时，物方焦平面上的箭头在像面上的位置不动，离焦的箭头在像面上的像随着光阑的位置变化发生上、下移动，但是在任何情况下，像面上的像与孔径光阑的位置相对应，同时也产生图像的畸变像差。

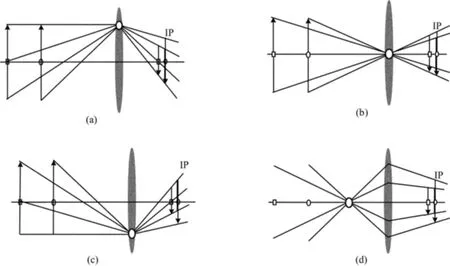
图4 小孔径光阑的位置对成像的影响

2.2 轴向对称孔径光阑移动时的成像规律

大多数相机镜头的孔径光阑都是轴向对称的，光阑的位置变化通常沿着光轴方向，尤其是变焦镜头，当倍率改变时，光阑在轴上的位置也发生改变。光阑在轴向的位置变化不仅产生成像点位置的移动，也产生镜头畸变像差，且这是镜头产生畸变的一个常见原因，光阑的位置决定了畸变的大小与正负（如桶形、枕形）。

由图4d可见，对于对称的小孔光阑向物方移动，离焦箭头的像变小，这证明了离焦的像与光阑的位置有关，因为光阑中心到镜头物方焦面上箭头的距离比离焦箭头相对更小。为了进一步说明问题，采用图5所示的有限孔径光阑来进行分析。在图5中，当孔径光阑落在镜头上时，主光线通过透镜后不改变方向，成像规律与图4b相似。当孔径光阑放在镜头的前方或后方时，主光线发生折射，孔径光阑中心沿着主光线到像和物点的距离比例决定了像的放大倍数h／y。当孔径光阑在镜头前方时，放大倍数减小；在镜头后方时，放大倍数增大。当物像的放大倍数是离轴距离y的函数时，空间直线在像面上的像将发生畸变。图5a所示为孔径光阑配置，系统的放大倍数h／y朝着像面拐角方向越来越小，产生桶形畸变；而图5b所示为光学配置，系统的放大倍数h／y朝着像面拐角方向越来越大，产生枕形畸变。

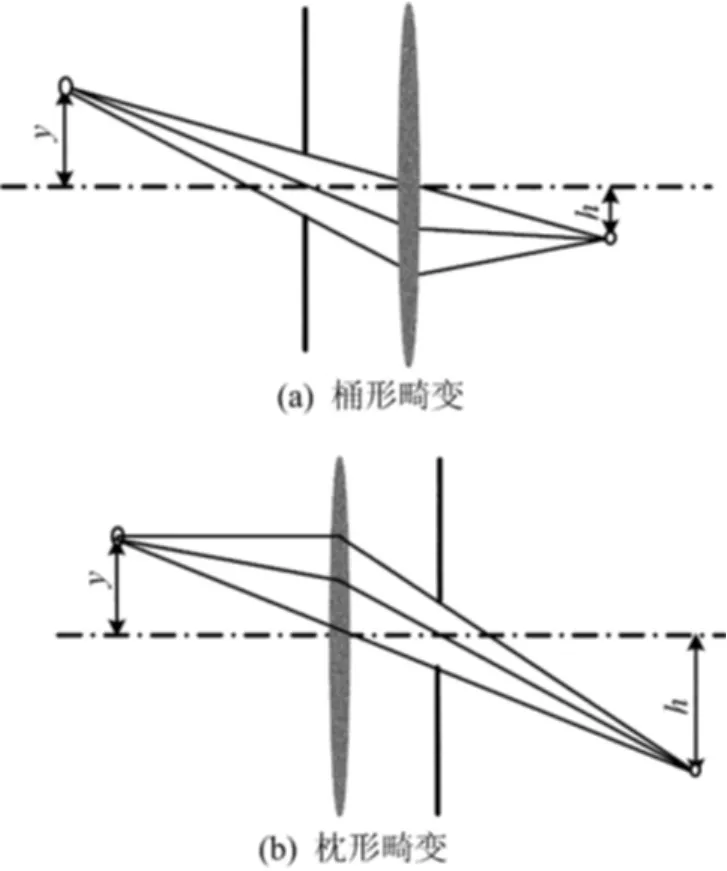
图5 孔径光阑的位置对成像的影响

光阑孔径的大小对畸变没有影响，因为主光线传播的路径并不随着孔径大小的改变而改变，但可以改善像差。在图5中，如果没有孔径光阑，成像系统将产生球差、慧差和像散等像差，这主要是物体上各点像的弥散斑综合效应产生的。对于复杂镜头（如retrofocus广角镜头）主要呈现桶形畸变，这是因为镜头前面镜片组相对于后部正镜组形成孔径光阑。摄远镜头后镜组是一组负镜组，会产生枕形畸变。在变焦镜头里畸变很难修正，因为镜头的畸变随着倍率的变化发生较大变化，在广角时呈现桶形畸变，随着倍率调整到摄远状态时，畸变变成了枕形畸变。对称镜头畸变最小，接近orthoscopic状态。通过改变光阑的孔径大小不能改变畸变的大小，但是可以控制其他像差。同其他光学像差一样，畸变大小与物体的距离有关，相同的镜头在远焦与近影时畸变是不同的。

3 镜头入瞳与透视中心的关系

镜头成像的大小、位置对畸变的影响与孔径光阑的位置有关，这表明镜头的透视中心与孔径光阑的位置有关。如图6所示，如果孔径光阑放置在镜头的后方，从物方透过透镜看孔径光阑的像，光阑的像的大小与位置会发生变化，这个孔径光阑在物方成的像称为透镜的入瞳。

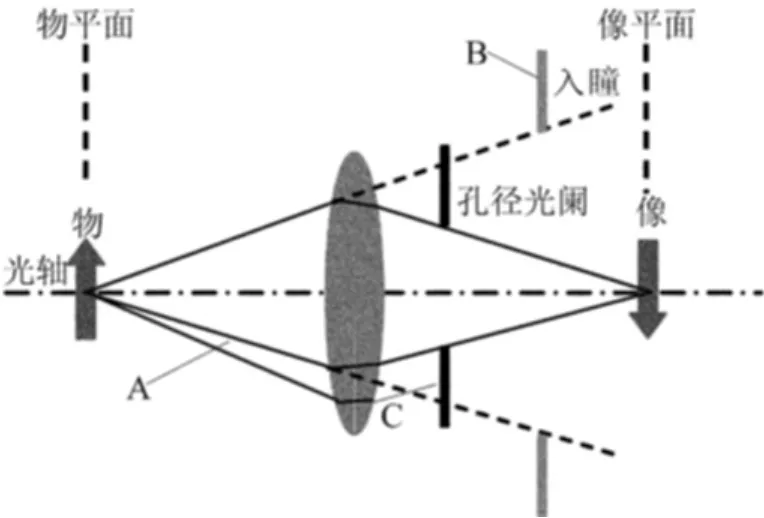
图6 孔径光阑与入瞳

图6中，“A”表示由于透镜折射通过孔径光阑的极限光束；“B”表示孔径光阑从物方看去所成的像；“C”表示被光圈阻挡的光束；入瞳是指透镜不存在情况下，极限光束对应的孔径光阑尺寸。

如果孔径光阑位于透镜的物方，从像方观看光阑的像，该像的位置与大小称为透镜的出瞳。根据入瞳和出瞳的定义，图6中的出瞳就是孔径光阑。对于一个实际镜头，入瞳和出瞳的位置同镜头的前节点位置并没有特殊的关系，直接射入前节点的光线并不一定能通过镜头，但直接射入入瞳的光线，将折射后通过孔径光阑，然后通过出瞳，在像面上成像，前节点同入瞳（透视中心）之间在位置上有时差别非常大。图7所示是一个镜头的光线追迹图［6］，从图中可以看出物理孔径光阑、入瞳及出瞳，前后主点位置之间的差别。从物方上面边缘的点直接射入到前节点的光线，没有通过入瞳，在通过镜头的过程中必将被孔径光阑阻挡，只有通过入瞳的光线才能穿透整个镜头，在像面上成像。

图7中，“A′”表示直接射向前节点的光束；“B′”表示直接射向入瞳的光扇；“C′”表示直接射向节点没有通过入瞳的光束不能穿透整个镜头；“D′”表示物理孔径光阑。

根据分析可知，镜头的透视中心确实在镜头的入瞳处，而不是在节点位置，即入瞳与光轴的焦点就是镜头的透视中心。厚透镜的透视模型及各基点之间的关系，如图8所示。

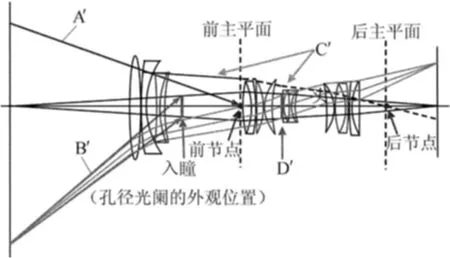
图7 镜头基点之间的关系

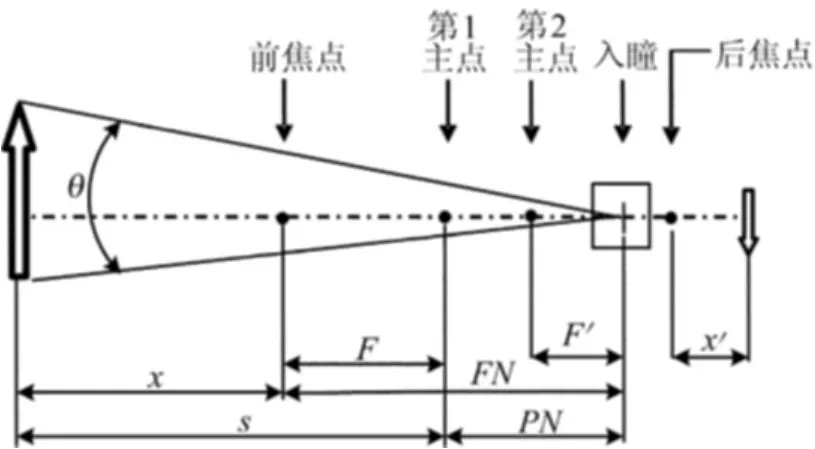
图8 透视中心与光学基点的关系

4 厚透镜视觉建模方法

对于大多数机器视觉镜头，都可以用一个厚透镜精确等效，如图9所示［9］。

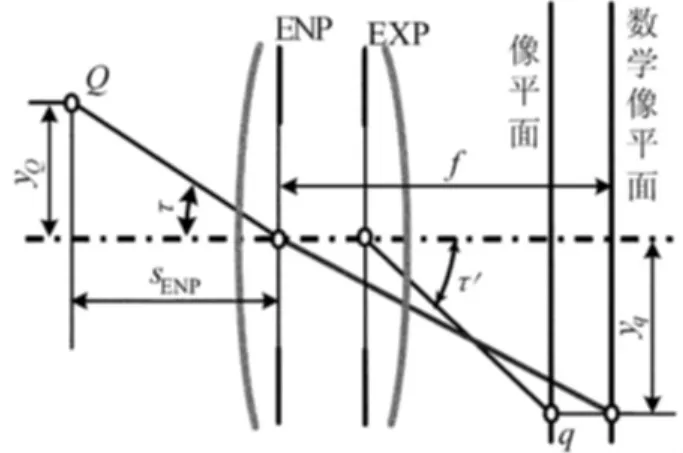
图9 相机镜头的厚透镜视觉透视投影模型

来自物体上Q点的主光线以入射角τ射入入瞳（ENP）中心，并以出射角τ′射出，与像平面相交形成Q点的像，但是入射角τ同出射角τ′并不相等。根据分析可知，入瞳中心是该镜头的透视中心，为了建立该厚透镜的视觉模型，从数学的角度上必须将像平面移动到一个新的位置，以得到一个虚拟的数学像平面（MIP），使Q点的像为Q点主光线的延长线与该MIP的交点，并且保持该像点位置与实际像平面的像点位置一致，MIP到入瞳平面的距离就是小孔视觉模型中等效焦距f，即

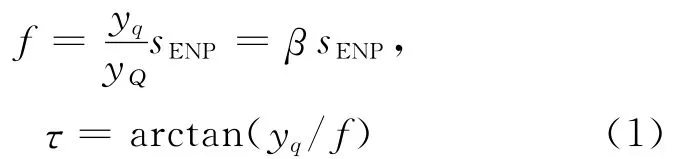
在变焦视觉测量中，尤其在PTZ测量系统中，上述模型非常有用，因为把镜头的入瞳中心调整到PTZ转台垂直轴与水平轴的交点（回转中心）位置，会使PTZ系统的视觉模型大为简化，使物体的极角计算独立于物距。如果透视中心与该回转中心不重合，物体上的点到回转中心的距离必须根据视觉模型计算结果进行修正，因为相机小孔视觉模型的坐标原点通常建立在透视中心位置，图10所示说明了2种之间的差异，其二维情况下的修正关系为：

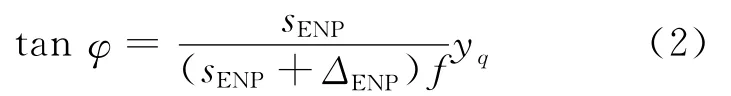
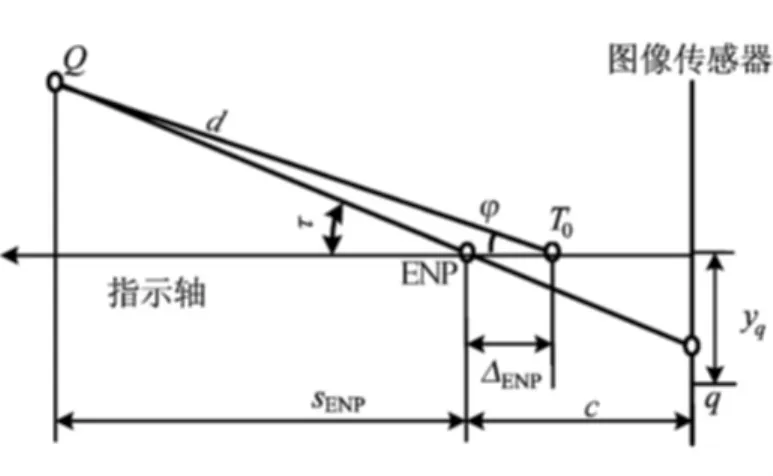
图10 回转中心与入瞳中心不重合带来的计算误差

5 透视中心位置实验验证

如图11所示，为了验证透视中心与镜头出瞳之间的关系，由相机、镜头、外加光阑和细线绷紧装置组成实验装置，镜头为Fujian GDS－35，F1.7 Lens，焦距为35mm，孔径为1.7mm。实验按照2种方式进行。

（1）光路中插入附加光阑和没有插入附加光阑2种情况下像的变化。在镜头前方放置2根相互平行、非常细的白色缝纫线A和B，2根线在光轴方向上前后放置，但尽可能离开光轴。在没有附加光阑的情况下，调整2根线的位置，使在计算机屏幕上看到2个稍微分开的像，然后调整镜头的焦距和镜头的光阑，使对焦面落在2根线的中间，2根线的像都比较清晰，且光阑的孔径尽可能敞开。再转动细线绷紧装置，轻微调整2根线的位置，使2根线以镜头本身的入瞳为透视中心，前后排列在一条透视投影线上，2根线的视场角相同，这样2根线在屏幕上的透视投影重叠，如图12a所示。在镜头的前方50mm左右插入附件孔径光阑，孔径大小约1mm，这时2根线的像分开，如图12b所示。该实验表明插入附加光阑后，成像系统的孔径光阑发生变化，透镜的入瞳变动到附加光阑的位置，透视中心发生了变化，变到新的入瞳处，导致2根线对入瞳的视场角大小不一样，因此A和B像相互分开。另外，从A和B像分开后的位置也可以看出，透视中心已经移到了镜头的前方。

（2）光路中插入附加光阑，且使光阑在垂直于光轴的平面内移动，观看像的变化，主要验证图4的成像效果。在镜头前方50mm左右处放置光阑，并把2根白色缝纫线A和B放置在附加光阑前方，按照前述的调整方式，使前后放置的线A和B在屏幕上的像重合。

然后在光轴垂直的平面内分别向左和向右移动附加光阑，这样可以看到2个重合的细线像，现在相互分开了，并且当光阑移到左边时，像A移动到左边，像B移动到右边。相反，当光阑移到右边时，像A也移动到右边，像B则移动到左边，如图13所示。

图11 实验装置与镜头

图12 孔径光阑位置变化对透视中心的影响

图13 光阑在垂直于光轴的方向上左右移动后的细线左右分开的图像

6 结束语

本文分析与研究了相机镜头孔径光阑与透视中心之间的关系，通过镜头的光线追迹和实验分析得到了镜头的透视中心在镜头的入瞳位置，这个结论在视觉变焦精密测量与跟踪定位及全景成像领域具有重要的应用价值。因为在通常的固定焦距视觉建模中，人们很少关注小孔视觉模型透视中心的真正物理位置，但在类似于PZT变焦视觉测量与跟踪系统及全景成像系统中，准确地把相机的回转中心调整到镜头的透视中心非常重要，这对提高模型的精度与减小后续图像处理的难度具有决定性的作用。通过本文分析，可知孔径光阑的位置不仅决定了镜头透视中心的位置，也是产生图像畸变的一个重要因素，但孔径光阑大小的变化对透视中心的位置没有影响，只能改变像点的光照度与模糊度。

［1］Kingslake R.Optics in photography［M］.Bellingham：SPIE Press，1992：1.

［2］Fayman J A，Sudarsky O，Rivlin E，et al.Zoom tracking and its applications［J］.Machine Vision and Applications，2001，13（1）：25－37.

［3］Haering N，Venetianer P，Lipton A.The evolution of video surveillance：an overview［J］.Machine Vision and Applications，2008，19：279－290.

［4］Wan D，Zhou J.Stereo vision using two PTZ cameras［J］.Computer Vision and Image Understanding，2008，112：184－194.

［5］Wan D，Zhou J.Self－calibration of spherical rectification for a PTZ－stereo system［J］.Image and Vision Computing，2010，28：367－375.

［6］Littlefield R.Theory of the No－parallax point in panorama photography［EB／OL］.（2006－02－06）.http：／／www.janrik.net／PanoPostings／NoParallaxPoint／TheoryOfTheNo－ParallaxPoint.pdf.

［7］Smith W J.Modern optical engineering：the design of optical systems［M］.3rd ed.McGraw－Hill，2000：21－60.

［8］张以谟.应用光学［M］.北京：电子工业出版社，2010：29.

［9］Bernd W.Development and calibration of an image assisted total station［D］.Zurich：Swiss Federal Institute of Technology Zurich，2005.