两不同截面串列方柱风力场特性的数值研究

王 辉， 韩 涵， 李新俊

（合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

在实际工程中，方柱是应用较多的结构体型并多以组合方式存在，如高层建筑、桥梁墩柱等。当组合方柱处于高雷诺数流场时，因截面外形特征及柱间流动干扰，流动特征复杂，涉及的漩涡脱落及场力特性区别于孤立的单柱流场。目前，组合圆柱流场的研究工作较多［1－5］，但相对缺乏组合方柱绕流特性的认识。对串列方柱，文献［6］考察了Re分别为2.76×104和5.67×104时间距对流场力的影响，指出流动模式转变的临界间距；文献［7］考虑了2×103＜Re＜1.6×104范围，研究串列组合绕流特征与雷诺数、间距的关系，指出流场力及斯特劳哈尔数Sr的变化规律；文献［8］分析了Re为100的组合绕流场，获得间距对流场特性的影响。对并列方柱，文献［9］研究了Re为2.31×104时的漩涡脱落频率特征；文献［10］对0.2262×104＜Re＜2.8×104时的柱间距影响漩涡脱落及流场力也开展了研究。组合绕流特性不仅取决于组合方式，截面尺度、Re等也为主要影响因素。已有研究所涉及的组合方柱均是相同截面，Re也小于105，考虑实际工程绕流所具有的高雷诺数特征，对组合方柱截面、间距影响绕流特性开展研究具有重要的理论和现实意义。

随着流体计算方法的发展，CFD方法已成为分析钝体绕流的有效手段［11］。本文采用大涡模拟（LES）方法，模拟两不同截面串列方柱（d／D＝0.5）于超临界范围（Re＝6.5×105）的绕流风场，分析间距对漩涡脱落及风力的影响，所获规律可为实际工程提供参考。

1 数值模型

对不可压缩流场，大涡模拟的运动控制方程，即滤波后的 N－S方程为［12］：

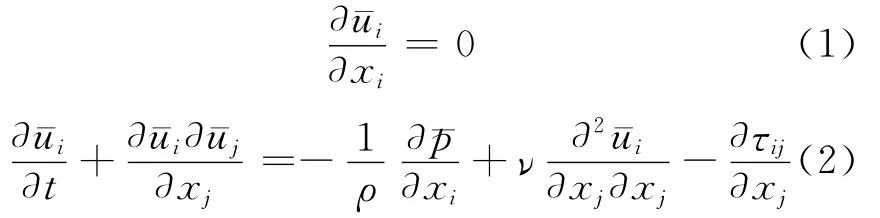
为封闭方程，采用涡黏模型构造亚格子应力张量τij与滤波后的应变速率张量的关系，表达式为：

2 模拟及分析

两不同截面方柱以串列方式组合，A柱置于迎风前方，排列方式及风向如图1所示，其中d／D＝0.5。考虑柱长远大于其截面尺寸，按二维流场分析其风场特性。

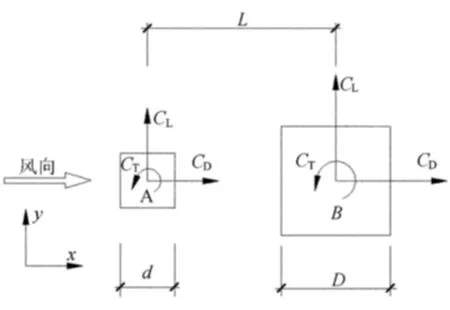
图1 组合排列示意图

设置计算区域时，以各柱截面中心为参考点，入口界面距A柱为7D，出口界面距B柱为30D，两侧界面距A或B柱则均为12D，以此保证湍流涡街的发展。采用贴体结构化六面体网格对计算区域剖分，适当加密壁面区网格，满足LSE对壁面网格尺度和分布的要求，如图2所示。

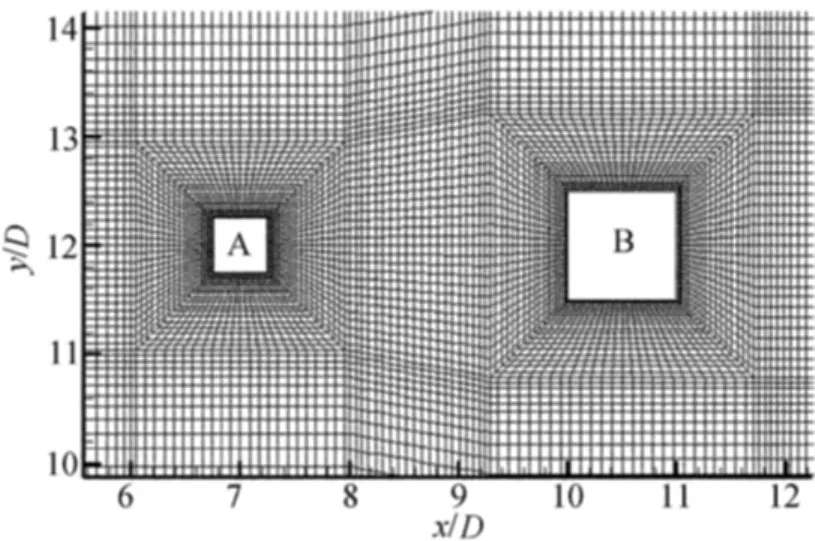
图2 局部贴体结构化网格剖分

流场控制方程采用控制容积法离散，考虑到漩涡脱落具有周期性，以A柱边长d作为特征尺寸预测漩涡脱落的周期，而时间步长则取小于1／50的预测周期值，满足分辨漩涡脱落主要周期特征值时对时间尺度的要求。迭代求解时，时间步内则由规定的收敛残差准则控制迭代次数，以时间推进求解。

风场雷诺数Re设为6.5×105（以B柱尺度为参数），两柱间距在0.75D≤L≤7.0D 区段变化。首先模拟单柱风场，获得的流场特征量见表1所列，表1中，Sr为斯特劳哈尔数为阻力系数时均值；CD′、CL′分别为阻力、升力系数均方误差。

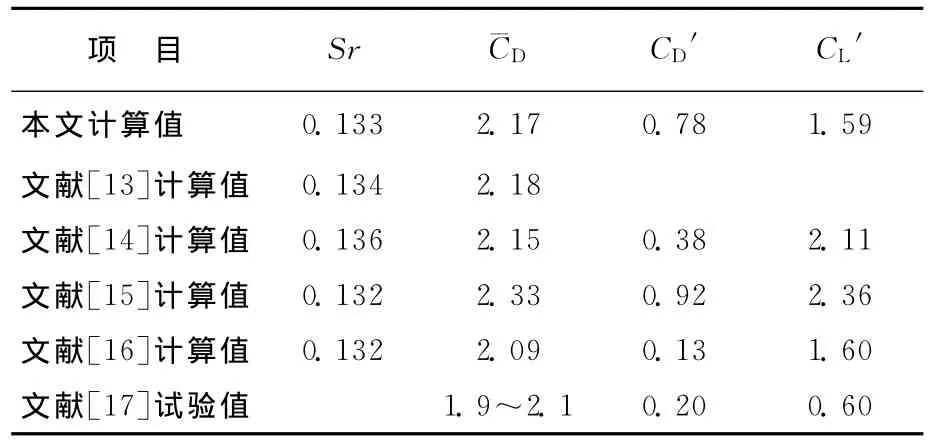
表1 单体方柱绕流场特征量计算值及与文献值比较

2.1 时均和脉动风力

图3所示为某4种工况的流线及风速等势图。当两柱接近时，间隙处流动较弱，两侧气流之间影响较小，显示出间隙对总体流动影响不显著，可近似认为两柱是无间隙的联体；随间距增大，间隙流动逐渐增强，A柱一侧分离流可沿间隙掺混到另侧的流动，混合该侧分离流作用于B柱，出现正面碰撞并在其迎风前角再次分离；当间距继续增大时，A柱尾流涡街的发展愈发充分，B柱则完全浸没于其尾流涡街中。

图3 4种工况的流线及风速等势图（U／U0）

2.1.1 时均风力

图4所示为各工况的时均阻力系数。图中，除小间距范围（L／D约小于0.9）外，A柱系数均大于B柱；L／D＝1.25为变化转折点，当L／D＜1.25时，A柱系数随间距增大而增加，但B柱情况相反；当1.5＜L／D＜3.0时，两柱的系数均有缓慢增加；当L／D≥3.0时，B柱系数基本趋于稳定，而A柱系数将逐渐接近单柱的数值。在整个间距变化范围内，串列柱的时均阻力系数均小于单柱情况。

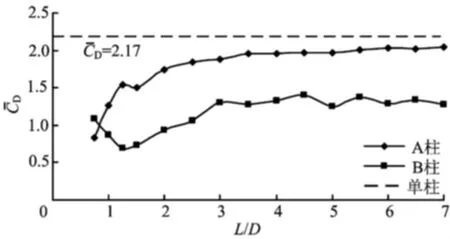
图4 时均阻力系数

2.1.2 脉动风力

图5～图7所示为L／D＝3.0时，A、B柱风力系数的时程曲线，时间参数以无量纲形式（tU／D）给出。图中，两柱所受风力脉动特征明显，B柱的阻力、升力和扭矩系数变幅最大值均大于A柱。图8所示为各工况的风力系数均方误差。

（1）阻力。L／D≤2.0时两柱阻力系数均方误差随间距变化明显；L／D＞3.5时A柱数值趋近单柱，表明B柱对A柱影响小；B柱数值在4.5时基本不变，在L／D＞4.5时才开始减小。

（2）升力。L／D≤2.0时，两柱升力系数均方误差随间距变化显著；L／D＞3.5时，两柱数值基本趋向稳定；L／D＞1.0时，A柱数值大于B柱。

图5 阻力系数时程曲线（L／D＝3.0）

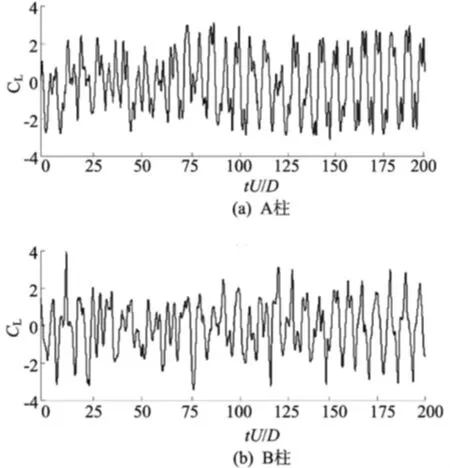
图6 升力系数时程曲线（L／D＝3.0）

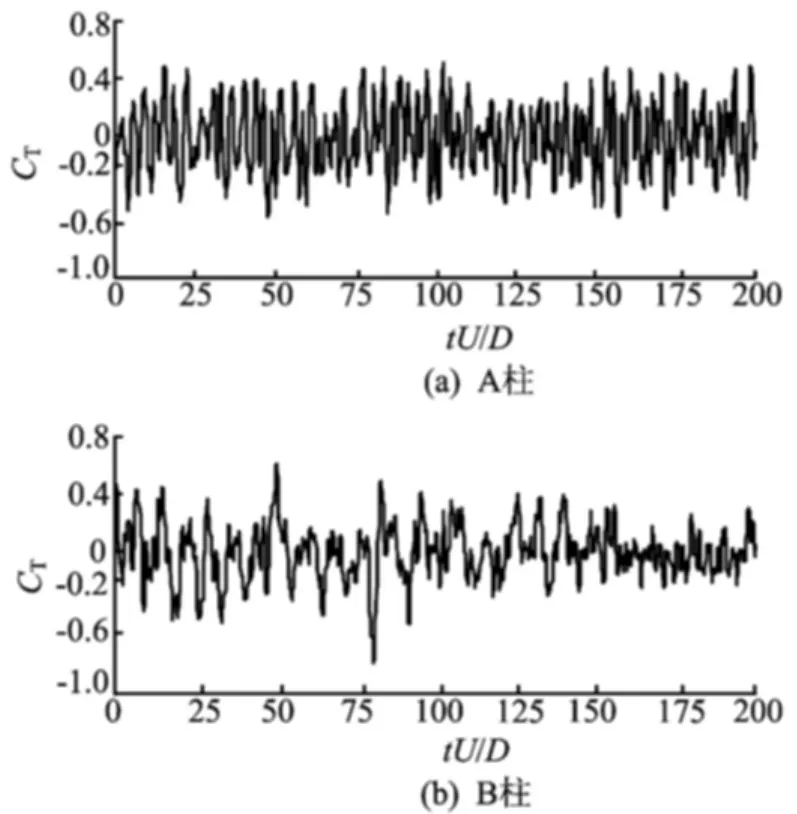
图7 扭矩系数时程曲线（L／D＝3.0）

图8 均方误差

（3）扭矩。随间距增大，A柱数值增加，而B柱则先增加后减小；L／D＞3.0时，两柱数值虽然有变化，但总体稳定。

比较上述风力系数均方误差与单柱数值，除B柱阻力系数均方误差在部分间距（L／D＝1.7～5.7）大于单柱外，其他情况下，串列柱的风力系数均方误差均可近似认为小于单柱，反映出串列组合能减小风力脉动值，而A柱数值随间距增大将趋近单柱，表明下风向B柱对A柱风力的影响随间距增大而减弱。

2.2 漩涡脱落特性

风场脉动力由漩涡脱落引起，通过对方柱升力时程的频谱分析，获得风场各工况的漩涡脱落主频，而斯特劳哈尔数Sr与漩涡脱落频率f存在如下关系：

其中，v为来流平均速度；D为截面特征尺寸。

图9所示为2种工况的升力系数频谱图，图中竖坐标最大值点对应的横坐标即为主频。由于两柱截面特征尺寸不同，但主频相同，表明两柱漩涡脱落频率存在锁定，根据单柱漩涡脱落的频率判断，B柱的涡脱频率被A柱锁定，与文献［18］的串列锁定现象吻合。文献［6］指出，对同截面串列方柱，仅当L／D≥27时，两柱才以各自特征频率独立脱落漩涡。本文模拟的组合方柱绕流的间距相对较小，因此所有工况均存在涡脱频率锁定现象。

图9 2种工况的升力系数频谱图

各工况两柱的斯特劳哈尔数Sr如图10所示。

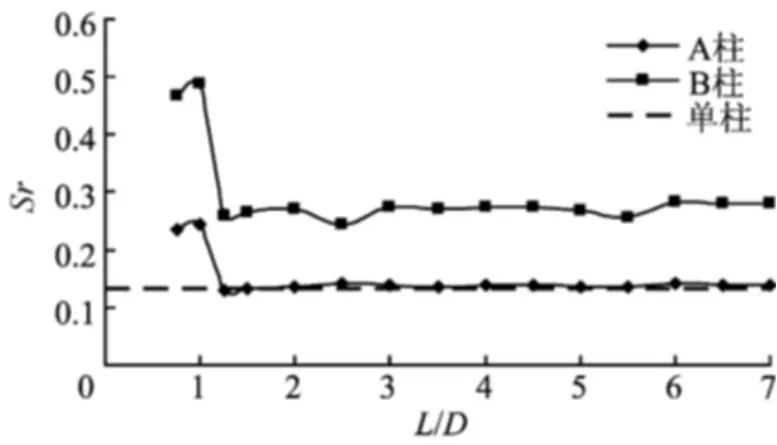
图10 两柱的斯特劳哈尔数Sr

图10中B柱由于涡脱频率受A柱控制，其Sr为A柱的2倍。间距很小情况时，由于等同联体的组合柱与方柱外形不同，因而其Sr值与方柱Sr值存在较大区别。随着间距增大，间隙流对两侧分离流的作用急剧增强，A柱Sr快速减小并趋向单柱Sr；当L／D＞1.25时，A柱Sr与单柱Sr基本一致，B柱对A柱的涡脱频率没有影响。

3 结 论

对2个不同截面串列方柱于某间距区段（0.75D≤L≤7.0D）的高雷诺数风场模拟分析后，获得以下结论：

（1）串列A、B柱的间距对两柱风力（时均和脉动风力）的影响表现在间距较小的范围；当L／D＜2.0时，风力变化比较显著；当L／D＞3.0时，风力变化较为平缓。

（2）与单柱比较，A、B柱阻力系数时均值均小于单柱，前列A柱可减小B柱的阻力系数时均值，并且这种影响随间距增大而趋于稳定；除B柱阻力系数均方误差在间距范围（L／D＝1.7～5.7）大于单柱外，可认为两柱风力系数均方误差均小于单柱；通过单柱与串列柱风力系数的比较，表明串列组合能减小两柱的风力，尤其是B柱风力。

（3）流场脉动特性由A柱的漩涡脱落决定，B柱的涡脱频率被A柱锁定；当两柱间距很小（L／D≤1.0），由于间隙流影响小，串列柱等同联体柱，其涡脱频率远大于单柱；随间距增大（1.0＜L／D＜1.25），涡脱频率明显减小并趋向单柱；当L／D≥1.25时，两柱涡脱频率保持稳定并与单柱一致。

［1］Sumner D.Two circular cylinders in cross－flow：a review［J］.Journal of Fluids and Structures，2010，26：849－899.

［2］Anagnostopoulos P，Dikarou Ch.Numerical simulation of viscous oscillatory flow past four cylinders in square arrangement［J］.Journal of Fluids and Structures，2011，27：212－232.

［3］Lam K，Lin Y F，Zou L，et al.Numerical simulation of flows around two unyawed and yawed wavy cylinders in tandem arrangement［J］.Journal of Fluids and Structures，2012，28：135－151.

［4］Vakil A，Green S I.Two－dimensional side－by－side circular cylinders at moderate Reynolds numbers［J］.Computers ＆Fluids，2011，51：136－144.

［5］Dehkordi B G，Moghaddam H S，Jafari H H.Numerical simulation of flow over two circular cylinders in tandem arrangement［J］.Journal of Hydrodynamics，2011，23（1）：114－126.

［6］Sakamoto H，Haniu H，Obata Y.Fluctuating forces acting on two square prisms in a tandem arrangement［J］.Journal of Wind Engineering and Industrial Aerodynamics，1987，26：85－103.

［7］Liu C H，Chen J M.Observations of hysteresis in flow around two square cylinders in a tandem arrangement［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90：1019－1050.

［8］Bao Yan，Wu Qier，Zhou Dai.Numerical investigation of flow around an inline square cylinder array with different spacing ratios［J］.Computers ＆ Fluids，2012，55：118－131.

［9］Kolar V，Lyn D A，Rodi W.Ensemble－average measurements in the turbulent near－wake of the two side－by－side square cylinders［J］.Journal of Fluid Mechanics，1997，346：201－237.

［10］Yen S C，Liu J H.Wake flow behind two side－by－side square cylinders［J］.International Journal of Heat and Fluid Flow，2011，32：41－51.

［11］Cochran L，Derickson R.A physical modeler’s view of computational wind engineering［J］.Journal of Wind Engineering and Industrial Aerodynamics，2011，99：139－153.

［12］Lilly D K.On the application of the eddy viscosity concept in the inertial subrange of turbulence，NCAR Manuscript No.123［R］.National Center for Atmospheric Research，Boulder，Colorado，1966.

［13］Bouris D，Bergeles G.2DLES of vortex shedding from a square cylinder［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，80：31－46.

［14］Franke R，Rodi W.Calculation of vortex shedding past a square cylinder with various turbulence models［C］／／Proc 8th Symp on Turbulent Shear Flows.Berlin：Springer，1991：189－204.

［15］Przulj V，Younis B A.Some aspects of the prediction of turbulent vortex shedding from bluff bodies［C］／／Proc ASME Annual Summer Meeting：FED，Vol 149，Washington，June，1993：75.

［16］Murakami S，Mochida A.On turbulent vortex shedding flow past 2Dsquare cylinder predicted by CFD［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，54／55：191－211.

［17］Cheng C M，Lu P C，Chen R H.Wind loads on square cylinder in homogenous turbulent flows［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，41：739－749.

［18］Alam M M，Sakamoto H.Investigation of Strouhal frequencies of two staggered bluff bodies and detection of multistable flow by wavelets［J］.Journal of Fluids and Structures，2005，20：425－449.