轿车后围板成形过程数值模拟及参数优化

吴华英，郭 成，王永信，张 露，王伊卿

(西安交通大学机械工程学院，西安710049)

传统采用经验方式进行覆盖件成形工艺设计，存在着试模周期长，成本高，模具寿命短等问题［1-2］.采用塑性有限元方法，对覆盖件的成形过程进行数值模拟，可以全面直观地了解覆盖件的整个成形过程，在设计前期就充分的考虑试模过程中可能会遇到的各类问题，进行模具结构的改进，得到合格的覆盖件零件.这是一种提高产品质量和生产效率的有效途径［3-6］.

为帮助企业生产出合格的零件，提高其生产效率，本文对某型号轿车后围板成形工艺设计和参数优化进行研究.主要研究内容有:对该零件所用材料B170P1进行单向拉伸试验，得到材料的力学性能参数;基于试验测定的材料参数，应用Dynaform软件对零件的成形过程进行模拟，优化拉延筋的受力及成形过程中的工艺参数;对成形之后的零件进行回弹分析及补偿.通过试模来验证研究所得成果.

1 板料力学性能参数的测定

1.1 单向拉伸试验

按GB/T3076-1982选取图1所示的尺寸进行板料的切割.根据标准要求，分别选取与轧制方向成0°、45°、90°的三个方向(图 2)，每个方向上制备三个试样在拉伸机上进行单向拉伸，测量板料硬化指数n、厚向异性指数r，取测量平均值，最终得到表1所示的结果.对比发现，测得的参数和软件材料库中的参数有较大偏差.

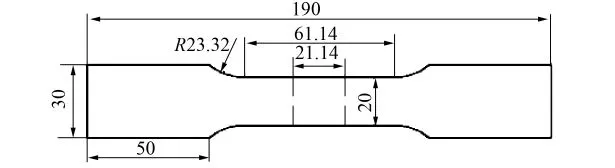
图1 标准样件尺寸

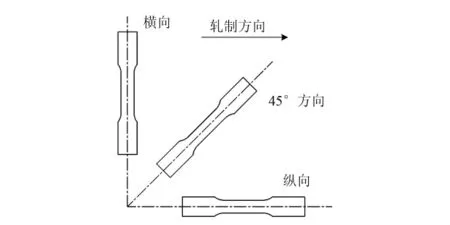
图2 试样截取方向

表1 测得的材料参数

1.2 板料力学性能参数测定的有效性

为了检验所测参数的有效性，分别利用Dynaform材料库和实际测量材料参数进行后围板(图3)的成形模拟，坯料尺寸为2 060 mm×1 260 mm矩形板料，与实际的拉延成形结果进行比较.

图3 后围板零件图

1.2.1 边界处的厚度变化趋势比较

如图4所示，取零件的四条边，在每条边上均匀的取12个点，测量其在采用软件材料库中参数、实际测量参数下的仿真厚度和实际试模产品厚度.测量结果见图5.

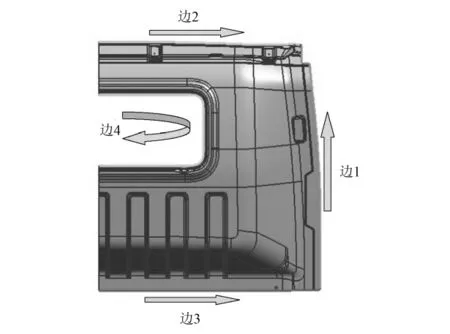
图4 测量厚度变化位置分布

从图5可见，采用实际测量的参数时，模拟的结果更接近实际试模的结果，边2上两者的结果基本一致.

1.2.2 整体成形效果的比较

图6是分别采用材料库中的材料参数、实际测量的材料参数和实际试模结果的比较.从图6(a)可以看出，采用材料库中的材料进行模拟的时候，板件大部分区域都处于安全区，没有出现破裂的区域.但是采用实际所测参数进行模拟的时候，零件在右上角的区域出现了破裂(见图6(b))，这与实际试模的结果一致(图6(c)).

从比较结果可知，采用实际测量板料力学参数进行的数值模拟更接近于实际试模结果.因此可以得出，在数值模拟之前，对材料的力学性能进行测定是非常有必要的，它可以有效的提高数值模拟的精度，解决实际试模中的成形问题，进而提高设计效率.

2 成形过程数值模拟与参数优化

2.1 成形过程的数值模拟及优化

针对后围板零件进行工艺补充面的设计，如图7所示(初步设计模型并未包含拉延筋)，进行无拉延筋时板料成形模拟，结果如图8所示，零件的周围出现了大面积的起皱，顶部出现未充分变形拉延区域.因此，需要设计拉延筋，以控制材料的流动，实现零件的顺利成形.

为了缩短计算时间，在Dynaform中根据经验设计的等效拉延筋布置见图9，同时，为了便于优化各处的拉延筋锁模力，把拉延筋分为5段，初步设计的拉延筋的截面图见图10.

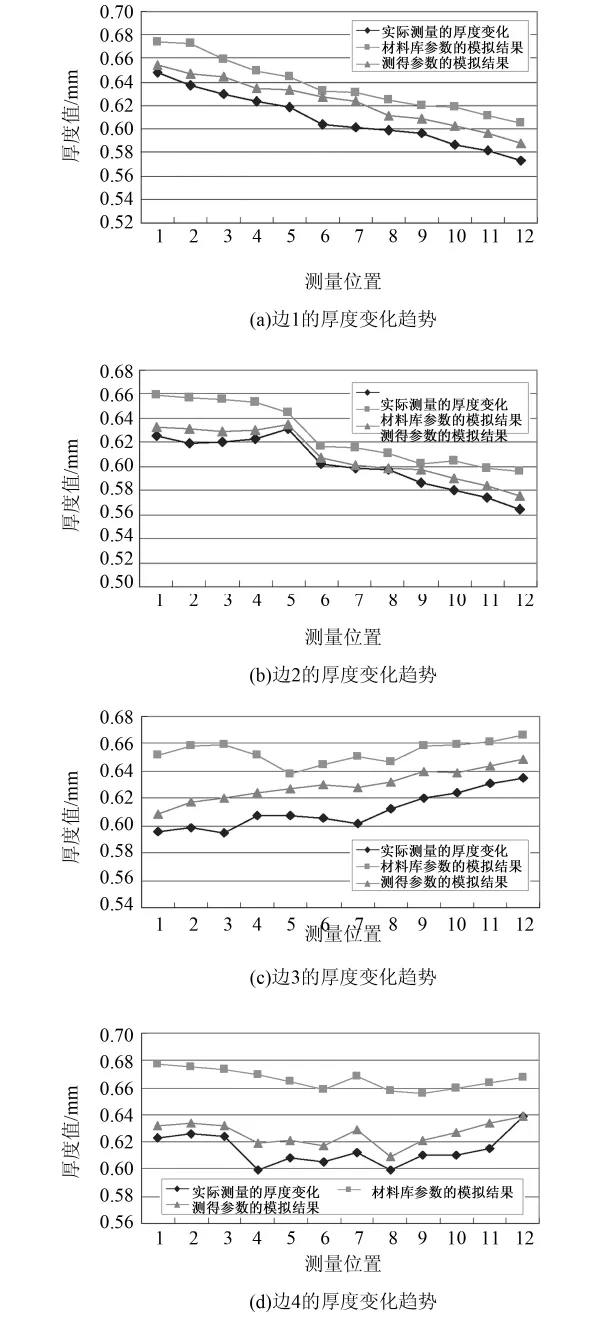
图5 不同位置的厚度变化趋势比较

将各拉延筋锁模力均设置成100%，模拟结果见图11:零件大部分的区域都得到了很好的拉延，但在其四周出现了大面积的拉裂现象，未设置拉延筋时(图8)，零件顶部已经有大面积变形充分区域.综合比较以上两个模拟结果，对不同位置的拉延筋设置不同的锁模力(图12)，将破裂比较严重的上侧和侧边部分的四条拉延筋设置成40%，下侧拉延筋设置成50%.

图6 整体成形效果的比较

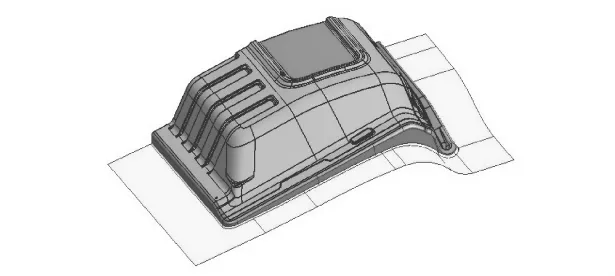
图7 初始拉延的CAD模型

对改进之后的模型再次进行分析，分析结果如图13所示:零件绝大部分区域都得到了充分的拉延，且都处于安全区域以内，没有破裂和起皱缺陷出现.但在零件的上侧，有一小部分区域仍具有破裂趋势，测得此处最大变薄率为22.84%，大于拉延成形中零件所允许的最大变薄率(20%).综合考虑，此处破裂趋势的产生可能还受到其他因素的影响，无法通过单独调节拉延筋的锁模力来完全消除.为得到满足要求的工艺方案设计，需研究分析影响成形结果的其他因素敏感性，获得主要影响因素进行调节，以消除此处的破裂趋势.

图8 无拉延筋的模拟结果

图9 拉延筋的分布图

图10 拉延筋截面

图11 100%锁模力下的模拟结果

2.2 正交试验优化成形过程中的参数

以正交试验［7］分析成形过程参数敏感性，选取零件在A区域(图13)最大变薄率作为评定指标，试验目的是把此处最大变薄率优化至20%以下.选取压边力，摩擦系数，拉延筋深度，凸凹模圆角半径四个经常调节的参数作为正交试验因子，各因子及其水平见表2.选取L9(34)标准正交试验表进行试验，结果见表3.

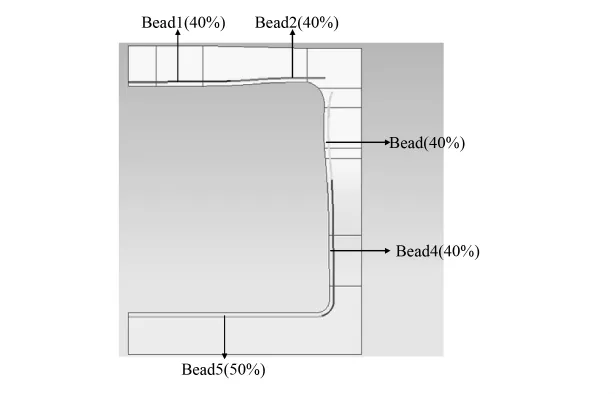
图12 优化之后的拉延筋力分布

图13 拉延筋优化之后模拟结果

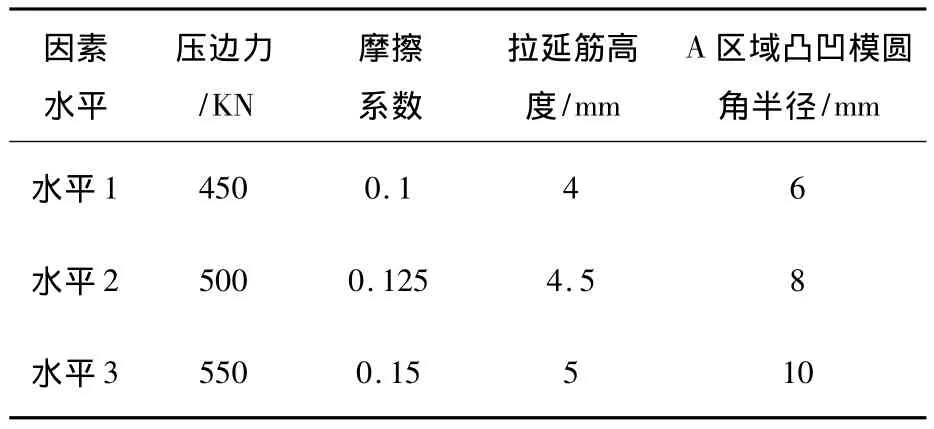
表2 正交试验各因子及其水平

对正交试验的结果进行分析可知，对最大变薄率影响最大因素先后次序为:摩擦系数、拉延筋高度、凸凹模圆角半径和压边力，影响参数最优组合为A2B1C1D3，即为:摩擦系数=0.1、拉延筋高度=4 mm、凸凹模圆角半径=10 mm、压边力=500 KN.利用该优化参数组合进行数值模拟，测得零件A区在此时的最大变薄率为17.8%(图14)，满足小于20%的要求，可见优化方案是合理的.

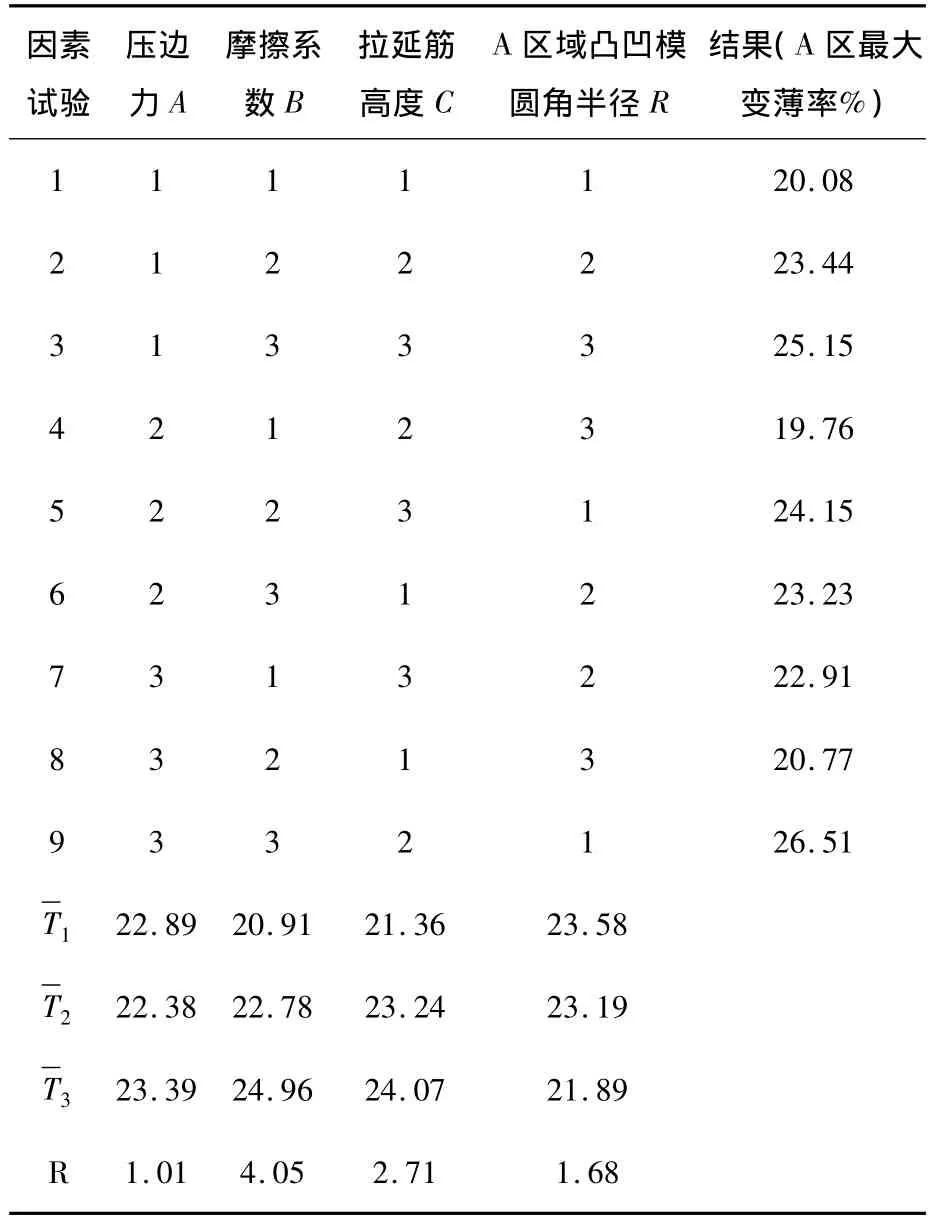
表3 正交试验的结果

图14 优化之后的模拟结果

3 回弹分析与补偿

3.1 回弹分析

回弹是实际工艺中很难有效克服的成形缺陷之一，它的精确预示是技术工程人员非常关心的问题.本文对成形零件进行回弹分析，并进行回弹补偿.图15是零件整体卸载之后的回弹变形.可以看出，零件最大回弹量达到4.71 mm，不过此处位于压料面上，在后边的切边步骤中，这部分的材料要被切除，因此不做过多的研究.分析最终零件的有效部分可知，回弹量分布主要集中在A、B、C三个区域，其中，A处最大变形量为1.58 mm，变形方向向上;B区最大变形量2.17 mm，变形方向向上;C区最大变形量2.35 mm，变形方向向下.

对零件进行切边，同时进行切边回弹分析(图16)，切边回弹的最大变形集中在A区和B区，其中A区最大变形量达到2.37 mm，变形方向向上，与前边整体回弹的结果相叠加，可以得到此处的最大变形量为3.95 mm.B处在切边回弹过程中最大变形量为4.99 mm，变形方向同样是向上，因此整个回弹过程之后，B处的最大变形量为7.16 mm.而C区域在切边回弹中的最大变形量是0.63 mm，变形方向向上，叠加之后，C区域的最大变形量为1.72 mm.

图15 整体回弹变形

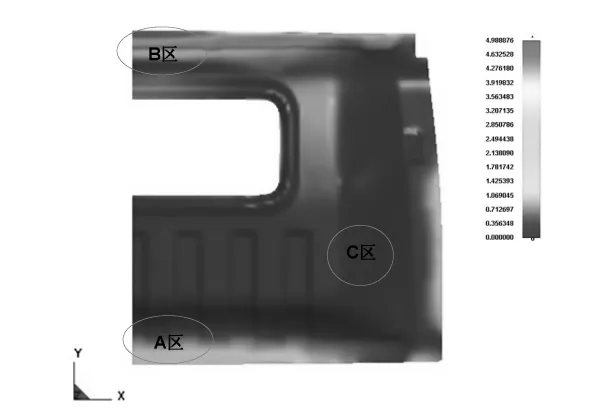
图16 切边回弹变形

在实际的生产中，企业所允许的回弹误差是3 mm，因此必须对这两处进行回弹补偿，以保证产品质量.

3.2 回弹补偿

本文采用补偿法［8］对零件的回弹变形进行补偿.将标准零件模型和最终回弹之后的模型同时导入到软件中，做截面线(如图17所示)，共得到20(回弹前后的零件各有十条)条截面线，再将其导入到UG中，对每对相对应的截面线分别进行比较，得到零件在不同截面边界处翘曲角度，如表4所示.

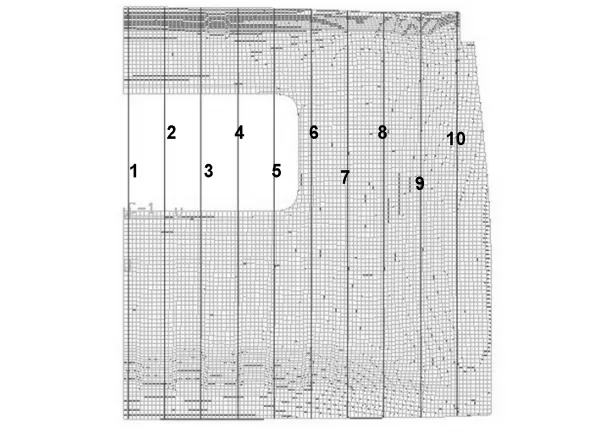
图17 截面线分布

图18 补偿区域分布

表4 截面线各处回弹角度值

由表4知零件变形主要集中在A、B、C、D、E五个区域，A区域对应的是零件左侧到截面“5”的上边部分，补偿3.94°;B区域对应的是截面“8”到零件右侧的上边部分，补偿1.65°;C区域集中在零件左侧到截面“2”的下部，补偿1.53°;D区域是截面“4”到截面“7”的下部，补偿1.25°;E区域是截面“8”到零件右侧的下部，由于回弹变形很小，不进行补偿，而在A-B、C-D、D-E之间的区域，均采用过渡方式进行补偿.补偿之后的CAD模型如图19所示.

图19 补偿之后的型面图

对补偿之后的模型再次进行成形模拟及回弹分析，测量模型左上角区域(也就是接近截面“1”上部的位置)的最大误差(之所以在此处进行测量，是因为根据前文可以知道，板件的最大变形量集中在左侧的上部，因整体的模型并没有太大的改变，因此回弹的最大区域也不会发生变化).图20显示模型左上角最大误差量(点1和点2之间的距离)为2.54 mm，小于企业要求的3 mm标准，因此利用补偿法减小了成型件的误差，满足了设计要求.

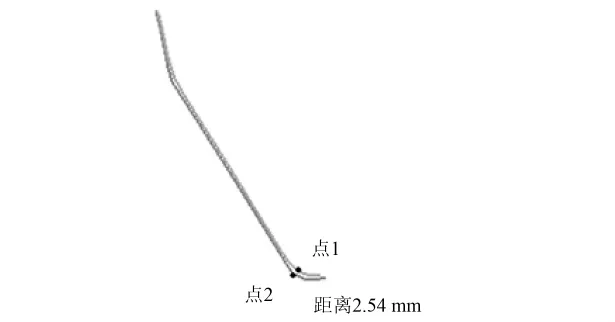
图20 补偿之后的最大误差

4 试模验证

按照回弹补偿之后的型面进行模具的设计及加工，并以优化之后的参数进行试模，最终得到合格成形件如图21所示.将最终的成型件安装到检具上，在零件的周围均匀的取点，测量其误差(如图22)，零件的最大误差为2.5 mm，满足企业的要求.

5 结论

1)板料力学性能实测参数的仿真结果更接近于真实工程数据，有助于提高数值模拟在工程应用中的仿真精度和指导价值.

2)仿真调整成形过程中拉延筋的受力分布，改进了板料流动均匀性，以此优化拉延筋结构形状，优化了模具成形工艺，提高了成形质量.

图21 最终成型件

图22 零件验收

3)应用正交试验对成形过程中的参数敏感性进行分析，明晰了对成形质量影响较大的主要影响参数，并针对性加以优化，提高了优化质量.

4)对零件进行仿真切边回弹分析，比较零件在不同截面边界处翘曲角度，通过补偿法对回弹变形进行了补偿，提高了模具成形质量，降低了回弹修模带来的风险.

综合以上结果可知，经验与数值模拟相结合的优化方法是提高产品质量及工艺设计效率的有效途径.

［1］张立文，陈磊，王富岗.板料超塑性拉延成形过程的数值模拟［J］.金属成形工艺，2002，1000-8446:01-0029-03.ZHANG Liw-en，CHEN Lei，WANG Fu-gang.Numerical Simulation of Superplastic Drawing Process of Sheets［J］，Metal Forming Technology，2002，1000-8446:01-0029-03.

［2］李建心.汽车覆盖件拉延工艺的关键技术研究［D］.济南:山东大学.2005.LI Jian-xin.Study on the key technology of auto-body panel forming process［D］.Jinan:Shandong University.2005

［3］NACEUR H，GUO Y.Q，BATOZ J.L，et al.Optimization of drawbead restraining forces and drawbead design in sheet metal forming process［J］.International Journal of Mechanical Science.2001，43:2407-2434.

［4］NACEUR H，GUO Y.Q.Response surface methodology for the design of sheet metal forming parameters to control springback effects［J］.Computers and Structures.2006，84:1651 ～1663.

［5］陈吉清，王兰超，兰凤崇.基于正交试验的汽车覆盖件冲压工艺参数优化［J］.计算机集成制造系统.2007，12(12):2440-2446.CHEN Jie-qing，WANG Lan-chao，LAN Feng-chong.Optimization for stamping process parameters of automotive body parts based on orthogonal experiment［J］，Computer Integrated Manufacturing Systems.2007，12(12):2440-2446.

［6］赵茂俞，薛克敏，李萍.多目标质量的覆盖件成形工艺参数优化［J］.机械工程学报.2009，45(8).ZHAO Mao-yu，XUE Ke-min，LI Ping.Auto panel forming process parameters optimization of multi-objective quality［J］.Journal of Mechanical Engineering.2009，45(8).

［7］刘小为.正交试验设计及回归分析方法［M］.西安:西安交通大学出版社，1983.LIU Xiao-wei.Design of orthogonal test and regression analysis method［M］.Xi′an:Xi′an Jiaotong University Press，1983.

［8］黄 霖，万 敏.铝合金厚板时效成形回弹补偿算法［J］.航空学报，2008，05:1406～1410.HUANG Lin，WAN Min.Compensation algorithm for springback in age forming for aluminum alloy thick plate［J］.Acta Aeronautica et Astronautica Sinica，2008，05:1406 ～1410.