逼近理想点法在航天器轨道优选中的应用

吴金美 ,侯亚威,胡上成,凌晓冬

(中国卫星海上测控部,江苏 江阴214431)

1 引 言

随着航天科技的飞速发展,航天任务对初轨精度的需求越来越高,一直以来,定轨算法和精度分析是航天领域的重要研究课题之一。但在实践中,由于参试设备多,数据量大,不管用什么定轨算法,最终都需要从多组定轨结果中优选出一组最优轨道。选优的方法直接影响了整个定轨的精度。最简单的做法可以按照比如轨道半长轴这样的重要分量进行排序,取中间的或取与平均值最接近的轨道方案。但只参考一个轨道分量的处理缺乏可信度,取中间值或平均值的做法缺乏系统的排序理论,这是轨道优选后定轨精度不高的一个重要原因,因此如何用一个系统的综合评价算法来进行的轨道选优,是测控中心也是海上测量船面临的一个问题。

航天器轨道有多个分量,均是重要的评价指标,缺一不可,其优选评价方法是一个多属性决策问题。多属性决策[1](Multiple Attribute Decision Making,MADM)是指在具有不可共度的多属性的情况下,利用已有的决策信息,通过一定的方式对有限个备选方案进行排序或择优。具体分析起来,简单易行的线性加权法要求各属性相互独立,故不能用来处理复杂的问题;层次分析法(AHP)将复杂问题表示为一个有序的递阶层次结构来计算,而初始轨道仅有6个轨道分量显然是不适用的;ELECTRE法需要建立优先关系,又难以确定;灰色关联分析法和逼近理想点法(TOPSIS)比较适合用来进行轨道选优,但这其中都牵涉到正负理想解的设定问题。杨永安[2-3]运用灰色关联分析法和逼近理想点法分别建立了卫星初始轨道选优模型,并进行了实例计算,虽然结果都比较合理,但其中灰色关联分析法中分辨系数的确定没有理论依据,逼近理想点法中对定轨方案增加了评价权重的做法仍值得商榷,而且两个模型中都将标称轨道作为目标轨道去计算理想解,标称轨道与实际轨道相差较大,必然影响精度,这也是最需要改进的地方。

本文考虑将TOPSIS方法应用到航天器初轨优选的问题中,着重解决目标轨道的计算和求解理想解的问题,建立相应的评价数学模型,并结合实例计算来验证模型的正确性。

2 用逼近理想点法进行轨道优选的基本思路

逼近理想点法是一种从几何观点出发的多属性决策方法,在m个属性下评估n个方案,类似于m维空间里的n个点,这是借助于多目标决策问题中理想解理想方案和负理想解负理想方案的思想。所谓理想解是一个设想的最好解,其各个指标值都达到各候选方案中最好的值,而负理想解是另一个设想的最坏解,其各个指标都达到各候选方案中最坏的值。在原方案集中对每个方案与正负理想解作比较,于是利用它们之间的距离信息即可作为对各个方案进行排序的标准,与正理想解越接近,与负理想解越远,方案越优。

TOPSIS方法主要分4个步骤,即建立规范化矩阵、求解正负理想解、求解各方案与正负理想解的距离、确定评价指数进行排序。应用到具体领域,针对不同的背景建立具体模型时最为关键的是规范化矩阵的构造和正负理想解的求解,对于轨道优选来说,中心处理系统将各设备的原始测量值进行处理后产生了多组初始轨道,每组轨道由6个开普勒根数来描述,分别是半长轴a、偏心率 e、轨道倾角 i、升交点赤经 Ψ、偏近点角 ω、近地点幅角 M,这6个指标就是每个轨道方案的6个属性,轨道优选问题就是根据这6个指标对多组轨道进行排序选优,确定出最优的轨道作为定轨的最终结果,而如何将这6个属性值化转为规范化矩阵,如何确定正负理想解,不同的做法将会得到不同的模型,也决定了模型的精度。

下面按照TOPSIS法的4个基本步骤建立轨道优选的数学模型。

3 轨道优选的数学模型

3.1 构造规范化矩阵

多属性决策问题中的不同属性之间可以相互比较重要性,但轨道根数6个指标无法给出具体权重,因此必须通过转换采用位置和速度的形式,才可以既保留每个方案的所有属性,又避免指标的相互关联以及权重的选择问题[2-4]。设有N组轨道方案,通过转换得到的其中第 i组的轨道在历元时刻在J2000.0惯性坐标系下的位置和速度为(xi,yi,zi,),统一表示为(pi1,pi2,pi3,pi4,pi5,pi6),其中 i=1,2,…,N。

上述轨道的6个指标并不是越大越好的效益型指标,也不是越小越好的成本型指标,为了能够参与计算,首先对多属性决策指标进行规范化,将6个分量计算成可以直接与“好”、“坏”相关联的指标。

事实上,如果将航天器飞行时真实轨道位置和速度表示为(p01,p02,p03,p04,p05,p06),将各方案轨道与其做差,差值为(ki1,ki2,ki3,ki4,ki5,ki6),其中则最理想的定轨结果就是与真实轨道差值为零。当然,由于各组设备的误差,定轨得出的轨道数据必然与真实轨道有偏差,差值是越小越好的成本型指标,并且,各评价指标权重相当,数量级也是一样的,不存在量级的差异以及权重的差别,因此差值不需要再进行加权和归一化,偏差矩阵可直接作为规范化矩阵,即

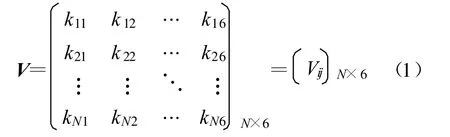
实际情况中,(p01,p02,p03,p04,p05,p06)未知,需要找到与此相近的轨道来代替,文献[2-3]用标称轨道作为这个目标轨道,这与真实轨道相差较大并不合理,而事实上现有的定轨结果与标称轨道相比较起来更为接近真实轨道,当然轨道优选本来就是选出其中最为接近真实轨道的那一组定轨结果,在优选结果出来前并不知道哪一组最近似,因此需要利用现有轨道方案进行处理得出一组数据用来近似真实轨道,作为目标轨道参与运算,这里,我们采用多组轨道结果进行加权平均求解目标轨道。

3.2 加权平均法求解目标轨道

由于测量机制有所差别,不同数据源确定的轨道的精度是不一样的,根据测控经验形成的共识,GPS数据确定的轨道精度较高,比较接近于真实轨道,遥测数据定轨又比外测数据定轨精度高,我们采用了10次任务的不同数据源定轨结果与精轨进行了比较,从10次任务的实测数据计算结果看,各类数据定轨结果的最大误差如表1所示。

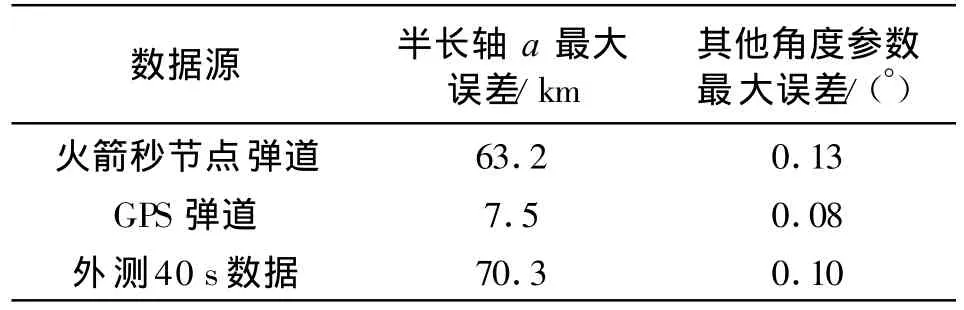
表1 各数据源定轨结果的偏差Table 1 Error of orbit determined by different data sources

可以看出,这与测控经验一致,相对于外测和遥测数据,GPS数据的定轨精度比较高,而遥测数据的定轨精度又比外测数据稍高。偏差越小,精度越高,与真实轨道越接近,在加权求解目标轨道的过程中所占比重越大,因此权重与偏差成反比,根据表1结合经验值我们将GPS、遥测、外测的定轨数据的权重之比定为 64∶8∶7,归一化后得 GPS、遥测、外测的定轨数据的权重为(0.81,0.10,0.09)。若外测数据源有n组定轨结果,每一组在加权时权重为若遥测数据源有m组定轨结果,每一组在加权时权重为

将加权求和所得到的目标轨道转化为J2000.0惯性坐标系下的位置和速度,记为(p01,p02,p03,p04,p05,p06),根据3.1节可计算得到规范矩阵 V。

3.3 确定评价对象的理想解和负理想解

6个属性指标是越小越好的成本型的,由

求得轨道方案各指标的正理想解和负理想解。正理想解和负理想解都是候选方案中没有的,正理想解的每个分量都达到各候选方案中最优的值,负理想解的各个分量都达到各候选方案中最差的值,逼近理想点法的基本思路就是找出虚拟的正理想解和负理想解,将各候选方案与正理想解和负理想解的距离进行比较,找出离正理想解最近同时离负理想解最远的方案。

3.4 计算距离

求解第i组候选方案与正理想解和负理想解的距离:

3.5 确定相对接近度,方案排序

第i组轨道方案与正理想解的相对接近度

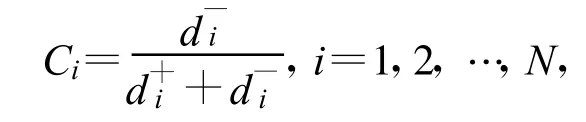
事实上,Ci的大小直接取决于方案与正负理想解的距离,与正理想解的距离越小,与负理想解的距离越大,Ci越大,方案越优。根据接近程度Ci从大到小的顺序,将各方案按优劣程度进行排序。

4 实例计算

4.1 例1

以同步卫星转移轨道为例,由测控系统各种数据源确定的6组轨道,如表2所示,列出6组轨道方案、火箭设计的标称轨道、事后处理得到的精轨以及加权平均法所得的轨道,将上述轨道根数转变为在历元时刻在J2000.0惯性坐标系下的位置和速度,见表3。用加权平均法得到的轨道作为目标轨道,按照轨道优选的计算步骤,依次计算偏差矩阵,以及正负理想解,进而计算出各轨道方案与正负理想解的距离以及相对接近度Ci,结果见表4～5。作为参照结果,用事后处理的精轨作为目标轨道,也按步骤进行排序计算,结果见表6～7。

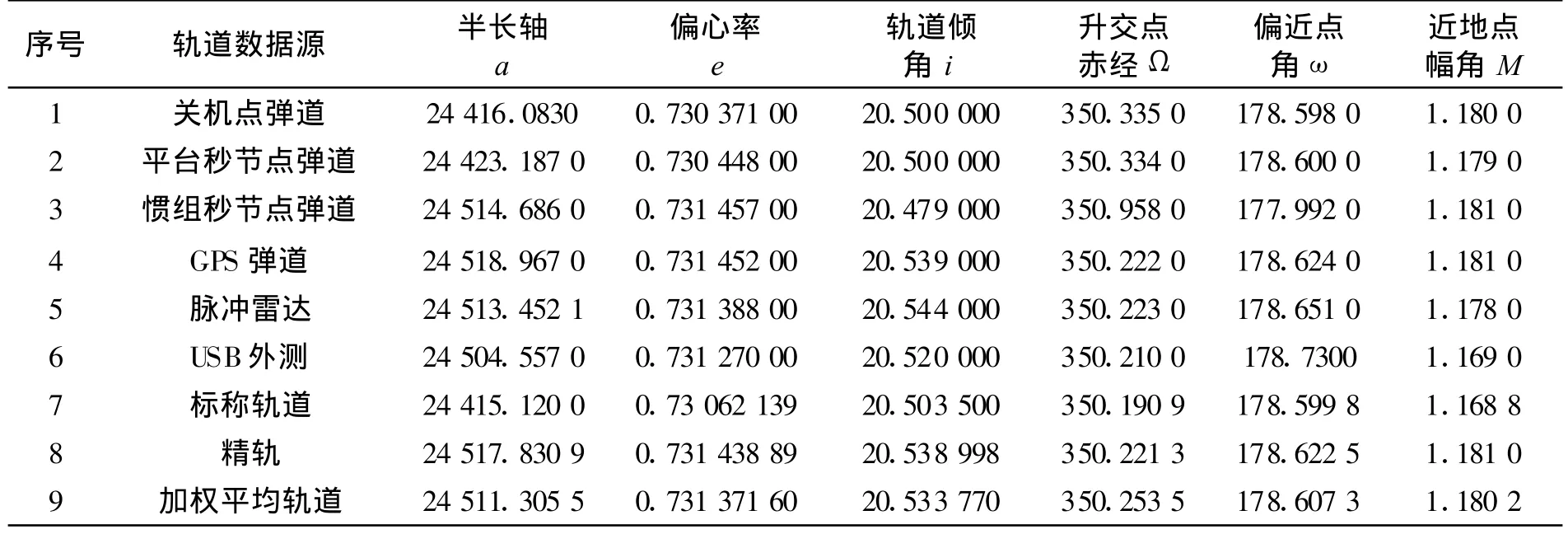
表2 轨道根数表Table 2 Orbit element

表3 位置和速度表Table 3 Position and speed

表4 规范化矩阵及正负理想解——加权平均轨道做目标轨道Table 4 Normalized matrix,ideal solution and negative solution ——set weighted average orbit as objective orbit

表5 评价指数以及排序——加权平均轨道做目标轨道Table 5 Evaluate exponent and ranking result——setweighted average orbit as objective orbit

表6 偏差矩阵以及正负理想解——事后精确轨道做目标轨道Table 6 Normalized matrix,ideal solution and negative solution ——set posterior precise orbit as objective orbit

表7 评价指数——事后精确轨道做目标轨道Table 7 Evaluate exponent and ranking result— —set posterior precise orbit as objective orbit

可以看出,两组计算结果一致,各方案的评价指数的值和分布也基本一致,均显示第五组轨道方案脉冲雷达最优,其次是GPS弹道,最差的是一组惯组秒节点弹道。事实上,从表3和表5就可看出,第五组脉冲雷达与第四组GPS弹道的轨道方案的各分量是非常接近于精轨和加权平均轨道的,偏差量最小,正理想解的各分量均取自第五组脉冲雷达或第四组GPS弹道的轨道方案,它们是6组轨道中最好的两组,其评价指标接近度也都是接近于1的且差别很小,其他各组方案的优劣程度也都符合对偏差的大小的分析。因此,用加权平均法计算目标轨道是精确的,用逼近理想点法建立的模型进行排序,计算结果是正确合理的。

为了对比,我们用标称轨道作目标轨道,也进行了轨道优选的计算,限于篇幅,这里只列出用标称轨道作目标轨道进行计算最终的评价结果,即6>2>1>5>4>3,这与前面两组结果相差较大,与直观的偏差分析也相悖,显然也是不合理的。事实上,精轨是事后处理得到的精确轨道,一般意义上即作为真实轨道,而标称轨道与真实轨道相差是比较大的,从表2即可看出标称轨道实际上与精轨相差比较大而加权平均法求得的轨道与精轨比较接近,说明标称轨道是不适合用做目标轨道的,会直接导致最终的排序结果不合理。

4.2 例2

以某太阳同步卫星为例,由测控系统各种数据源确定的10组轨道以及标称轨道、精轨和加权平均法得到的目标轨道,按照前面给出的模型进行轨道优选的计算。限于篇幅,这里只列出轨道根数表以及用加权平均轨道、精轨、标称轨道做目标轨道得到的最终结果,如表8和表9所示。

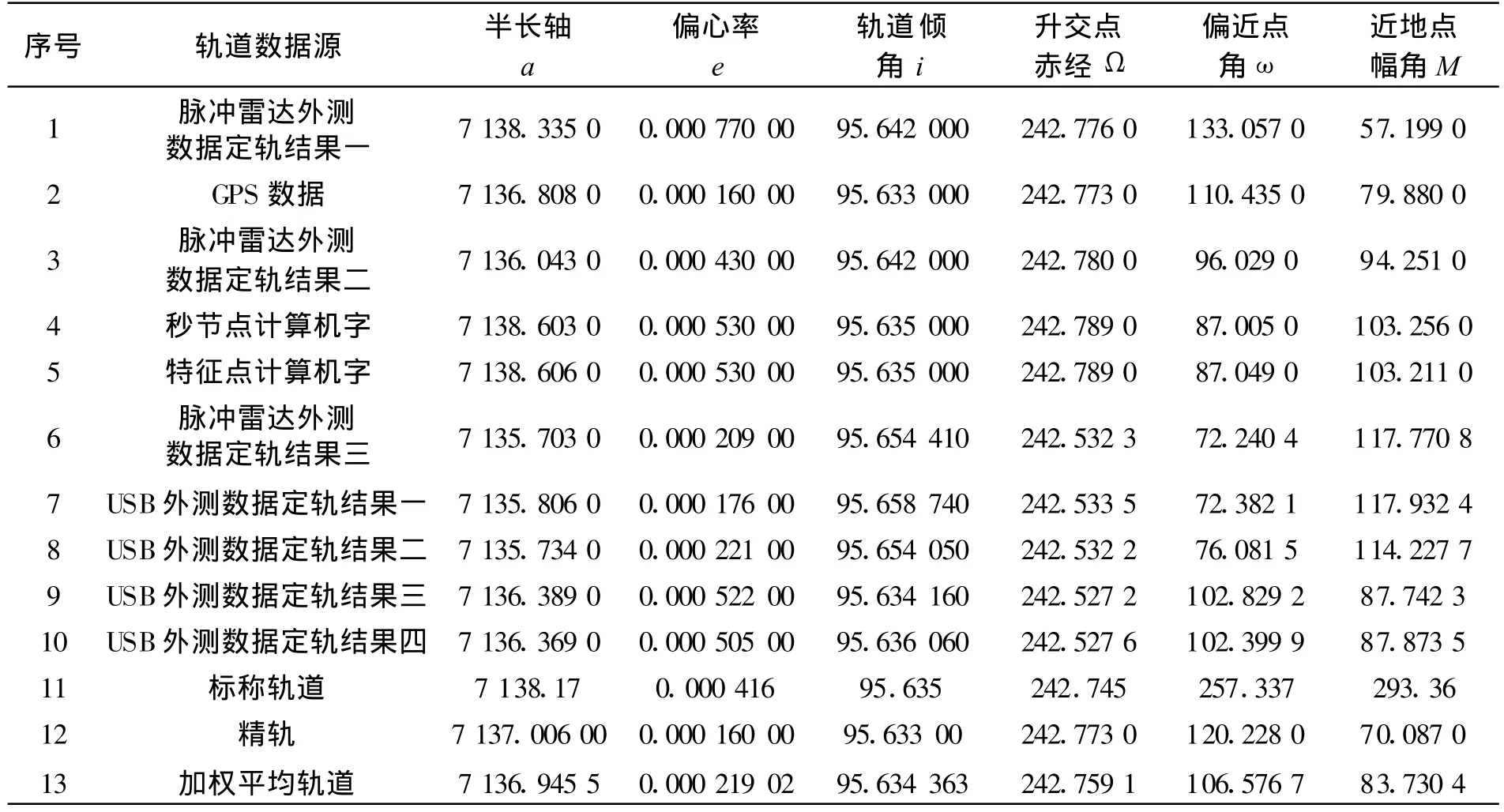
表8 轨道根数表Table 8 Orbit element

表9 排序结果Table 9 Ranking results

用加权平均轨道和事后精确轨道做目标轨道得到的最终排序基本一致,最好的轨道方案都是第二组GPS弹道,只在排名第二和第三的轨道位置有所变化,事实上第一组轨道方案和第三组轨道方案在两次计算结果中评价接近度都是很相近的,所以排序也是相近的,优劣程度也相差不大,排序的先后变化是可以接受的,所以模型和结果是正确合理的。加权平均法求得的轨道也是比较接近精轨的,在实时处理中可作为目标轨道进行计算。

而用标称轨道作目标轨道的最终的评价结果与前面两组结果相差较大,从直观的偏差分析和测控经验就可得出排序显然是不合理的。

5 结 论

本文提出的逼近理想点法解决航天器轨道优选问题的模型,能够给出轨道优选的合理正确的排序,满足轨道初选的实时性和精确性的要求。从实例计算结果可以看出,其中的加权平均法求解目标轨道与直接用标称轨道做目标轨道相比,精度显著提高。当然,在实践应用中,还需要对模型进一步完善,优选结果的精度主要取决于加权平均法求解的目标轨道的精度,权重的变化对结果会有一定的影响,本文确定的权重求得的目标轨道是比较精确的,但还需要通过大量的系统仿真和统计进行验证和分析,有待进一步更为深入的研究。

[1]刘培德.基于模糊多属性决策的企业信息化水平评价方法与应用研究[D].北京:北京交通大学,2009:56-78.LIU Pei-de.Study on Evaluation Methods and Application of Enterprise Informatization Level Based on Fuzzy Multi-Attribute Decision Making[D].Beijing:Beijing Jiaotong University,2009:56-78.(in Chinese)

[2]杨永安,魏峻,冯祖仁,等 .灰色关联分析法在卫星初轨优选中的应用[J].系统工程与电子技术,2008,30(2):308-311.YANG Yong-an,WEI Jun,FENG Zu-ren,et al.Application of grey relational analysis methods in optimal selection of satellite initial orbits[J].Systems Engineering and Electronic,2008,30(2):308-311.(in Chinese)

[3]杨永安,冯祖仁,张宏伟,等.基于逼近理想解排序法的航天器初始轨道选优[J].宇航学报,2006,27(4):106-109.YANG Yong-an,FENG Zu-ren,ZHANG Hong-wei,et al.An Approach to Optimizing the Initial Orbital Elements of Spacecraft Base on TOPSIS Method[J].Journal of Astronautics,2006,27(4):106-109.(in Chinese)

[4]杜小宁,李瑛,耶刚强,等.粒子群算法的航天器初始轨道优化模型[J].哈尔滨工业大学学报,2011,43(5):144-148.DU Xiao-ning,LI Ying,YEGang-qiang,et al.An optimizing model of initial orbit of spacecraft using PSO[J].Journal ofHarbin Institute of Techonlogy,2011,43(5):144-148.(in Chinese)

[5]李济深.人造卫星精密轨道确定[M].北京:解放军出版社,1995:220-228.LI Ji-sheng.Satellite Precision Orbit Determination[M].Beijing:PLA Publishing Company,1995:220-228.(in Chinese)

[6]张守信.外弹道测量与卫星轨道测量基础[M].北京:国防工业出版社,1992:125-131.ZHANG Shou-xin.Outer-Trajectory Measurement and Satellite OrbitMeasurement[M].Beijing:National Defense Industry Press,1992:125-131.(in Chinese)

[7]岳超源.决策理论与方法[M].北京:科学出版社,2003:204-244.YUE Chao-yuan.Theory and Methods of Decision[M].Beijing:Science Press,2003:204-244.(in Chinese)