多频段高动态信号载波频偏捕获方法研究

丁 丹 ,程乃平何攀峰

(1.装备学院 光电装备系,北京 101416;2.装备学院 研究生院,北京102249)

1 引 言

随着飞行器技术的发展,飞行器之间通常具有很高的相对径向速度和加速度,这使得双方通信接收机接收信号的载波具有很大的多普勒频率(高达几十kHz,甚至上百kHz)和多普勒频率变化率(可高达数kHz/s),即存在很高的动态,因此需要首先进行载波频偏捕获和校正。另外,不同飞行器的信号频段有所差异,带来的多普勒频偏也不同,因此研究多频段载波频偏捕获问题具有十分重要的意义。

目前,载波频偏捕获方法中大多是基于FFT的捕获方法。对于MPSK调制信号,通过M次方变换来消除调制信息,进行FFT处理,求得最大值谱线对应的频率即作为FFT粗估计频率值,采用FFT的谱线位置和相位进行插值就可以精确地求得载波频偏。由于FFT估计存在“频谱泄露”,插值算法可以进一步细化估计频率。目前插值算法较多,常见的有抛物线插值法[1]、Rife插值法[2]、Quinn插值法[3]、多点插值法[4]等。文献[1]分析了抛物线插值和Rife算法,对Rife算法进行改进,分析了补零对性能的影响,指出抛物线插值法适合于补零FFT情况,即高信噪比条件下的短码捕获。改进的 Rife算法在不补零时估计误差较小,补零时估计误差较大。文献[5]分析了 Rife法、Quinn法的估计精度,分析了加窗函数对估计性能的影响,指出加汉明窗能提高Rife法性能。由于FFT有成熟的算法,且插值方法的计算复杂度较小,但对于基带信号经过脉冲成形后,M次方并不能完全去除调制信息,而低信噪比会加剧这种情况,因此,FFT粗估计难以正确估计频偏,插值方法也随之失效。

2 多频段载波频偏最大功率搜索算法

本文提出的最大功率搜索法可以捕获大频偏,信噪比门限较低,且不需要数据和定时信息的辅助。最大功率搜索的思想是假定发送数据是独立同分布的,对于存在频偏的调制信号,给一定的频偏补偿后,再经过匹配滤波器进行滤波,之后计算信号的能量,若在某一频偏 ωj补偿下能量最大则认为ωj就是频偏估计量[6]。最大功率搜索估计频偏的方法如图1所示。

图1 最大功率搜索估计频偏方法Fig.1Maximum power search method of frequency offset estimation

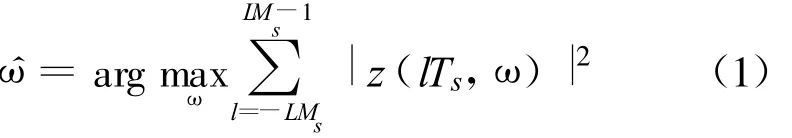
其中,为下变频后的信号经过频偏为 ω补偿后匹配滤波的输出信号,L为处理信号的长度。为了能够估计出频偏,假设最大频偏为fdmax,由于在频域要使得信号无衰减,由奈圭斯特低通采样定理可知:假设采样率为fs,抽取倍数D应该满足:fs/2D>B+fdmax,其中B为信号成型后的单边带带宽,B=(1+α)/2T,α为滚降系数,T为符号周期。

考虑到时域和频域对应关系:时域卷积和域频相乘等价。将估计式转到频域估计,频偏估计值为[4]

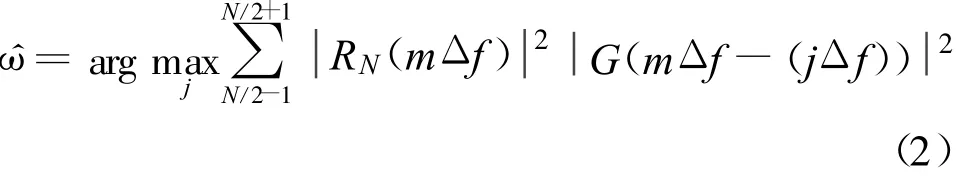
考虑到多频段的影响,对接收信号进行不同倍数的抽取,在大频偏下采用较小的抽取倍数,小频偏下采用大的抽取倍数,对抽取后的信号利用平均周期图法计算信号的功率谱,在与频移jΔf的匹配滤波器功率谱相乘求得最终功率,若在某一jΔf下功率最大,则认为jΔf为估计的频率。估计结构如图2所示。

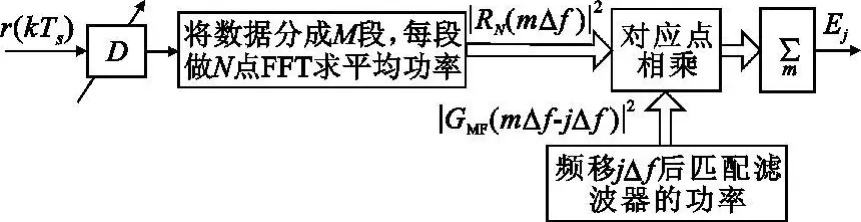
图2 最大功率搜索频域估计结构Fig.2 Frequency domain estimation structure of maximum power estimation

3 仿真分析

仿真条件:采用QPSK调制方式,最大载波频偏设为3.5 kHz(UHF频段)或20 kHz(S频段),取数据率为9.6 kb/s,滚降系数为 α=0.35,以超过门限的概率、估计的归一化方差(用符号率来归一化方法)以及估计偏差这3个参数来衡量该方法的性能,其中门限为FFT的分辨率Δf(由于搜索步长为FFT的分辨率Δf)。

3.1 与传统方法的比较

假设频偏估计是直接处理下变频经过D倍抽取后的信号,数据率为9.6 kb/s,滚降系数为0.35。

(1)UHF频段捕获性能比较

UHF频段最大载波频偏为3.5 kHz,为了兼顾两种方法对对采样率的要求,取采样率为4倍数据率。数据长度为128个符号,并分段,每段进行128点FFT取平均,在不同信噪比条件下,M次方后直接FFT估计和最大功率估计性能如图3所示。

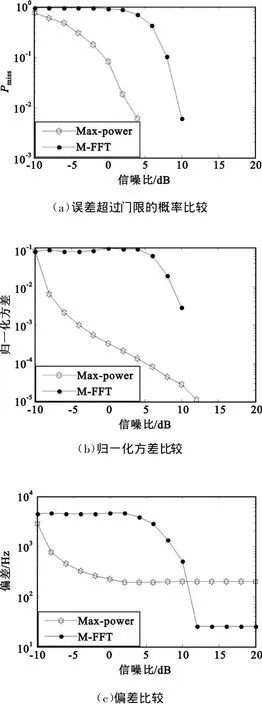
图3 UHF频段下两种方法估计频偏的性能Fig.3 The performance of the two methods in UHF band

从图中可以看出,当信噪比在10 dB以下时,最大功率法无论是误差超过门限的概率、归一化方差还是偏差都要小于M次方后FFT的估计方法;当信噪比超过10 dB时,M次方后FFT的方法,估计误差超过门限的概率及归一化方差与最大功率法相当,但是估计偏差较小。

(2)S频段捕获性能比较

S频段最大载波频偏为20 kHz,取采样率为信号17倍数据率,数据长度为32个符号,并分段,每段进行128点FFT后求平均功率谱,在不同信噪比下,直接FFT估计和最大功率估计性能如图4所示。

图4 S频段下两种方法估计频偏的性能Fig.4 The performance of the two methods in S band

可以看出,当信噪比在-5～18 dB这个区间时,最大功率法的性能要好于 M次方后FFT的估计方法;当信噪比达到20 dB时,虽然M次方后FFT的估计偏差较小,但是估计误差超过门限的概率及估计归一化方差仍然比最大功率法估计要大。相比较而言,最大功率估计方法是性能较优的方法。

3.2 不同符号长度下性能分析

符号率 Rb为9.6 kb/s时,取 fs=4Rb,分别在符号长度为64、96、128时,在不同信噪比条件下,做128点FFT,得到的估计性能见图5。从图5中可以看出,符号长度的增加,降低了误差超过门限的概率,降低了估计方差和偏差。

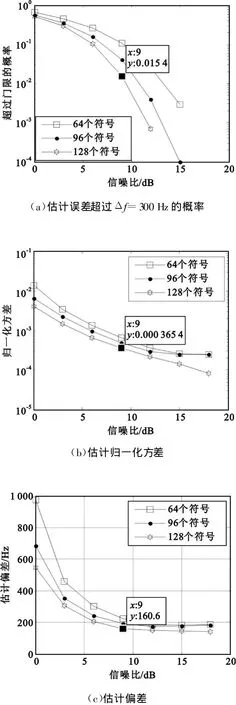
图5 不同符号长度下性能Fig.5 The performance under variant symbol length

由于FFT点数一定,采样率一定,则分辨率也一定,符号长度的变化直接导致分段数的变化,即采样率越高段数越高,采用平均周期图法计算接收信号的功率,则采样率增加相当于增加平均的次数。平均周期图法的方差为[5]

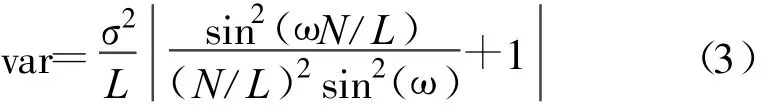
其中,N为处理信号的长度,L为分段的段数。可见段数L的增加会减小方差特性。即平均次数增加能够改善功率谱的方差特性,从而改善捕获性能。

3.3 抽取倍数和符号长度的选择

由于最大功率搜索法的采样率fs和抽取倍数D满足 fs/2D>B+fdmax,令f′s=fs/D为抽取后的采样率,滚降系数 α为0.35,分别计算得到UHF频段和S频段的抽取后的采样率至少为19.96 kHz和52.96 kHz。采样率为0.6144MHz(即64倍符号采样),抽取倍数分别满足为D<31、D<11。

为了同时兼顾分析精度、误差超过门限的概率、估计偏差,采用128点FFT,信号的功率谱估计采用4次平均,通过仿真实验得到相应的抽取倍数及处理符号长度及其性能见表1。

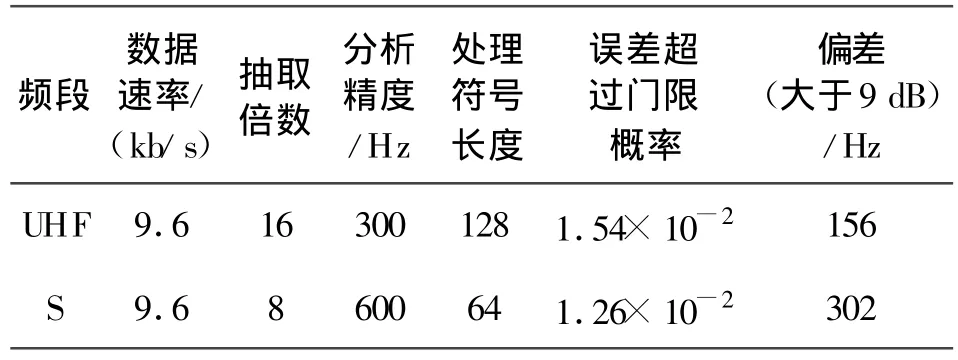
表1 UHF频段和S频段抽取倍数和处理符号长度选择Table 1Decimation time and symbol length in UHF and S band

4 结束语

本文针对多频段载波频偏捕获问题,考虑到低符号率、大频偏的影响,基于频偏补偿后功率最大的思想,提出了最大功率载波捕获方法。理论分析和仿真结果表明,相比于传统的FFT+插值法,最大功率法对不同频段的适应能力更强,捕获信噪比门限更低,运算量不大且能保证一定的精度。该方法已成功应用于某卫星通信系统,效果良好。

[1]章兰英,袁嗣杰,陈源.航天扩频测控系统中伪码捕获方法研究[J].电子学报,2011,39(6):1472-1476.ZHANG Lan-ying,YUAN Si-jie,CHEN Yuan.Research on Pseudo Code Acquisition Method in Aerospace Spread Spectrum TT&C System[J].Acta Electronica Sinica,2011,39(6):1472-1476.(in Chinese)

[2]朱磊,董亮,刘树东.基于Quinn算法与改进的Rife算法的正弦信号频率估计[J].大庆石油学院学报,2010,34(1):98-101.ZHU Lei,DONG Liang,LIU Shu-dong.Sine signal frequency estimation based on the algorithm of Quinn and improved Rife[J].Journal of Daqing Petroleum Institute,2010,34(1):98-101.(in Chinese)

[3]Quinn B G.Estimating frequency by interpolation using Fourier coefficients[J].IEEE Transactionson Signal Processing,1994,42(5):1264-1268.

[4]Belega D,Dallet D,Petri D.Accuracy ofSine Wave Frequency Estimation by Multi-point Interpolated DFT Approach[J].IEEE Transactions on Instrumentation and Measurement,2010,59(11):2808-2812.

[5]齐国清.几种基于FFT的频率估计方法精度分析[J].振动工程学报,2006,19(1):86-92.QI Guo-qing.Accuracy analysis and comparison of some FFT-based frequency estimators[J].Journal of Vibration Engineering,2006,19(1):86-92.(in Chinese)

[6]Meyr H,Moeneclaey M,FechtelS A.Digital Communication Receivers.Synchronization,Channel Estimation,and Signal Processing[M].New York:Wiley,1998.