基于VB的全站仪任意设站曲线测设程序的实现

张 庆，李 龙，路文利，姜 楠，侯安业

（1.淄博矿业集团有限责任公司,山东 淄博 255120；2.山东科技大学 测绘学院,山东 青岛 266590；3.菏泽市测绘研究院 ,山东 菏泽 274000； 4.青岛市妇女儿童医院 ,山东 淄博 266011）

运用偏角法、切线支距法、弦线支距法等传统曲线测设方法工作时，需要考虑实际工作中的现场条件、测设数据求算的繁简、测设工作量的大小以及测设时仪器和工具情况等因素。因此，在实际工作中利用上述传统测设方法，有时会因地形条件的限制而无法放样出辅点，或放样出的辅点处无法设置标桩。为此，本文在对各种曲线测设方法进行了系统分析的基础上，结合日常工作中线路测设的经验，克服了以往采用Excel表格计算繁琐、导入数据易出错等缺点，结合曲线测设现场的实际情况，对不通视段的曲线测设进行了程序的编制，更大地满足了复杂地段曲线测设的需求。

1 任意站测设曲线原理

选取一个尽量能看到整个曲线的点作为控制点,反算曲线上各点到该点的距离、方位,然后在实地进行拔角、量距测定放样点。该方法关键是求出曲线上各点的坐标值，在曲线放样中曲线上的直圆点(ZY)、直缓点(ZH)、圆直点(YZ)和缓直点(HZ)的坐标由设计人员提供，依据这些数据,通过一定的坐标转换,得到所需的平面坐标系中的坐标。如图1所示，为便于曲线测设，将坐标ZH点设在坐标原点的位置。

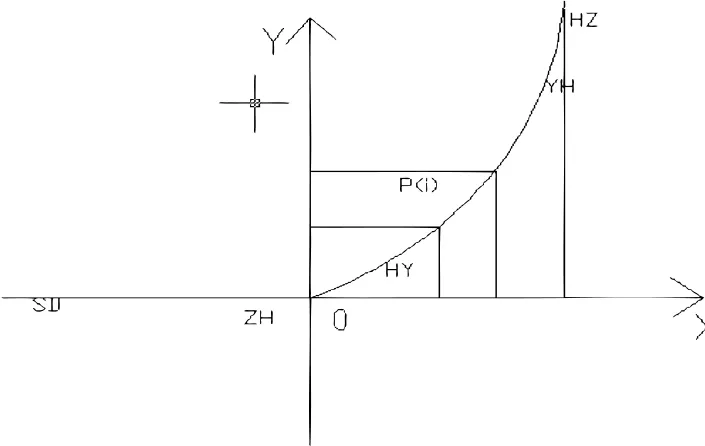
图1 曲线测设示意图

2 软件介绍及案例分析

2.1 数据的预处理

首先根据现场的踏勘要求，拟定合适的曲线测设方案。通过CAD模拟，确定测设曲线的半径、偏角大小以及缓和曲线的长度（如图2所示）。由于把直缓点定义在了坐标原点上，所以直缓点初始坐标为（0,0）。

图2 设计计算方案

2.2 曲线综合要素的计算

设圆曲线的半径为R，两端缓和曲线长为l0，曲线转向角为α，即可计算切线长T，曲线长L，外失距E0和切曲差q等要素（如图3所示），计算公式如下：

图3 曲线综合要素计算

2.3 ZH-HY段的独立坐标计算

以∆l为步长改变li ,按切线支距法计算第 P点的独立坐标，设li =Li−L0，Li和L0分别为i点和ZH点的里程。

1）若 P在 ZH-HY段 ,则：

2）若P在HY-YH段，则：

式中，li为自ZH点起的曲线长；l0为缓和曲线长；R为圆曲线半径 。

2.4 独立坐标转换为平面坐标

设独立坐标系X(ZH)Y的圆点ZH的平面坐标为（x0，y0），X轴的坐标方位角为a0，a0与方位角aKD−JD一致，方位角由在线路定测阶段测得的和点JD的平面坐标反算得到。点 KD为线路直线段上的1个里程桩点。X0、Y0可由点JD的平面坐标及方位角aKD−JD和切线T反算得到，切线T据式(4) 计算。

则独立坐标系中任一点 P (x，y)的平面坐标X、Y为：

坐标平差计算部分代码为：Debug.Print "The A matrix is:"

ShowMatrix a

MatrixTrans a, At '求A的转置矩阵

Debug.Print "The At matrix is:"

ShowMatrix At

Debug.Print "The P matrix is:"

ShowMatrix P

Matrix_Multy AtP, At, P '求AtP

Debug.Print "and The AtP matrix is:"

ShowMatrix AtP

Matrix_Multy Naa, AtP, a '法方程系数矩阵

Debug.Print "the Naa matrix is:"

ShowMatrix Naa

Debug.Print "the L matrix is:"

For x1 = LBound(L) To UBound(L)

Debug.Print L(x1)

Next x1

Matrix_Multy W, AtP, L '法方程常数向量

Debug.Print "the W matrix is:"

For x1 = LBound(W) To UBound(W)

Debug.Print W(x1)

Next x1

MajorInColGuass Naa, W, x

Debug.Print "the X matrix is:"

For x1 = LBound(x) To UBound(x)

Debug.Print x(x1)

Next x1

表1为独立坐标的计算结果以及放样的坐标。

经过独立坐标运算之后的坐标并不是所需放样点的坐标，最终的坐标需要经过坐标转换，通过设计点与实际现场监测点的匹配，计算出转换参数，进而得到最终的放样点坐标，如表2所示。

3 测设中线桩的精度分析

在测设当中遇到误差是在所难免的，主要的误差有2个部分：测设数据的误差和在测设过程中存在的误差。测设数据(水平角βK和水平距离DPK) 是由3个点坐标计算出来的,其中中线桩K的坐标不含误差,另一控制点A 的坐标误差略去不计,影响测设数据的主要是测站点P 的坐标误差。其精度计算公式为：注：表中DAP、DPK单位为m，测设精度单位为mm。

表1 独立坐标计算结果

表2 平面坐标计算结果

表3 测后中线桩K的精度统计/mm

可以看出: ①在保证测站精度的条件下，测设中桩的点位误差与测设距离呈反比变化。②当测设距离一定时,点位误差随测站点位置不同而有所变化。尤其是测站点距控制点很近,又要测设很远的距离时,点位误差将急剧增大。当距离控制点距离较大时，从30 m到300 m，误差仅仅差10.6 mm，趋于稳定，说明在保证测设精度情况下，测设中测站点设站应尽量离已知点远一点。

4 结 语

本文主要解决了以下问题：

1）通过任意站测设，测站的设置摆脱了地形的限制，可以灵活地选择测站点进行放样，在地势复杂区域显示其优势。

2）通过程序运算进行放样的方案设计，简洁直观，计算机计算准确，出错率低，提高了测设的精度。

3）进行一次设站可以放样出几乎所有的待放样点，测设效率大大提高，而且本文也进行了越障碍曲线的提设，巧妙地减少了重复设站的繁琐工作，进一步提高了曲线测设的效率。

[1]李青岳,陈永奇.工程测量学 [M].第三版.北京：测绘出版社，

[1]李青岳,陈永奇.工程测量学 [M].第三版.北京：测绘出版社，

2008

[2]李宏奎，孙树海，苏慎龙.在任意点设站进行不通视直线段测设[J].露天采煤技术,2002(2):43-45

[3]靳海亮,吴庆忠.全站仪任意设站测设曲线[J].矿山测量,2004(1):43-45

[4]刘金凤.全站仪自由设站法及精度分析[J].江西测绘,2007(12):12-15

[5]王江,杨旭辉.全站仪在曲线测量中的应用[J].铁道标准设计,2002(11):18-21

[6]臧军强，许永发.曲线任意点坐标计算与测设[J].隧道建设，2003（3）:53-58

[7]甘延续，孙瑞泰.曲线坐标放样快速计算程序[J].隧道建设,2004(1):68-70

[8]彭仪普.任意站极坐标法测设线路平面曲线探讨[J].铁道工程学报,2001(1):43-45

[9]徐玉田,申志明.自由设站测设曲线[J].勘察科学技术,2002(5):55-57