全长粘结岩石锚杆拉拔数值模拟
张 凯, 杨 庆*,, 蒋 景 彩, 孙 亚 军
(1.大连理工大学 土木工程学院 岩土工程研究所,辽宁 大连 116024;2.德岛大学 土木与环境工程系,日本 德岛;3.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
0 引 言
岩体工程的失稳多是由于内部节理、裂隙等缺陷的萌生、发展、扩展和贯通等过程而导致.为了提高岩体的稳定性,人们大多采用各种施加锚杆的手段进行加固.其中,边坡和地下洞室是应用锚固技术最早也最广泛的一个领域.一般而言,锚杆加固的作用十分明显,不论是对岩体节理面抗剪强度的加强,还是对岩体松散区和连续区的连接,都能维系岩体工程的长期稳定.更重要的是,岩石锚杆还具有一定的柔性,既能够适应岩体节理扩展时产生的适度变形,又能控制岩体多节理面之间的完全贯通破坏.
长期以来,为了指导工程实践,人们对锚杆锚固段的应力分布规律及其随外荷载增大应力变化的趋势进行了大量研究.最早大都采用锚固段界面剪应力均匀分布的假设[1],后来大量试验表明该假设仅适用于破碎岩体及砂土中[2].Phillips[3]提出锚固界面剪应力呈指数函数分布,但其最大剪应力在锚杆最外端的假定与试验结果不吻合.尤春安[4]将岩体及锚固剂联合体视为等效线弹性材料,以此作为基本假设,结合Mindlin位移解推导出全长粘结性锚杆轴力及界面剪应力的分布公式.杨庆等[5]也得到全长注浆岩石锚杆应力分布形式为指数分布的结果,并给出了注浆体诸多特性参数对锚杆极限承载力的影响.张季如等[6]和刘建庄等[7]都给出锚杆荷载传递的双曲函数分布模型,但给出的曲线衰减系数略有不同.
全长注浆锚杆的拉拔试验经常会被用来确定锚固强度和锚固质量,可以更好地协助锚杆设计.Farmer[8]通过大量试验,研究拉拔荷载作用下锚杆的力学性状.他指出,锚杆在较大拉拔荷载下会出现界面处的“解耦”,即部分失效.上述纯指数或双曲线分布的研究成果只适用于锚杆-砂浆截面未产生剪切破坏的弹性情形,对于界面剪切破坏后锚杆的承载能力,并未做出有效的分析.
本文借鉴以往研究成果,采用界面剪应力重分布假设,定义出界面剪切刚度的变化曲线,利用ABAQUS软件自带的弹簧模型,对典型拉拔试验进行数值模拟,并与前人的试验结果进行对比.
1 理论研究
1.1 拉拔破坏机理
锚杆的锚固段是由筋材、注浆体及周围岩体构成的多介质复合体[9],因而具有复杂的力学特性:材料非线性、几何非线性、非均质性和非连续性.但很多试验表明破坏大多发生在筋材-注浆体界面,因此为了力学分析简化,可将其近似为具有单一界面的复合材料,不影响力学规律的求解.通过拉拔试验中对锚杆轴向应力的测量,可以得到破坏过程中界面剪应力的分布(图1).

图1 全长注浆岩石锚杆锚固段的粘结应力分布[10]Fig.1 Distribution of bonding stress of full-grouted rock bolt in fixed length[10]
根据界面剪应力分布的变化,构建了两种不同大小拉拔荷载作用下的受力模型.在拉拔荷载较小时,锚杆处于弹性状态,所受粘结力与其位移成线性关系,剪应力呈负指数曲线分布(图2),剪应力峰值产生在锚杆端部;随着拉拔荷载增大,端部剪应力超过材料容许剪应力,锚固体首先产生横向破坏和断裂,继而剪切破坏,并由围岩外部逐渐向内部扩展.由于锚固体在锚杆端部最先发生剪切破坏,由此造成锚杆-砂浆界面剪应力峰值向岩体深部转移.此时,锚杆的受力特征发生明显改变(图3),根据受力情形可将其由外至内划分为4个区域:失效段、破坏段、软化段和弹性段.失效段在锚杆的端部,长度较小,一般视为端部剪切破坏的极端情况,即完全失去承载能力;破坏段紧接着失效段,该区域提供砂浆体破坏后所提供的残余强度,界面粘结力由摩擦阻力取代;弹性段表示该区域锚杆依然保持破坏前的弹性状态,受力状态与之前相似;软化段连接破坏段和弹性段,近似为受力状态从原粘结力到最终摩擦阻力的线性过渡.
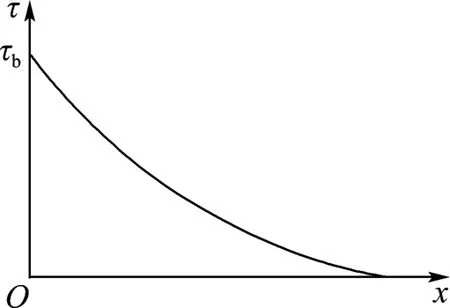
图2 拉拔荷载较小时的锚杆-砂浆界面剪应力分布模型Fig.2 Distribution of shear stress in bolt-grout interface under small pull-out load

图3 拉拔荷载较大时的锚杆-砂浆界面剪应力分布模型Fig.3 Distribution of shear stress in bolt-grout interface under large pull-out load
1.2 锚固段受力分析
根据力学平衡关系,对上述各个区域段进行了界面剪应力和锚杆轴向应力的求解.
(1)失效段(0≤x<x0)

(2)破坏段(x0≤x<x1)

(3)软化段(x1≤x<x2)

式中:Δ(=x2-x1)为过渡段长度,ω(=Sr/Sp)为残余强度峰值与粘结剪切强度的比值.
(4)弹性段(x2≤x≤l)

1.3 粘结剪切刚度系数
Li等[11]在其论文中提出利用砂浆及岩石剪切模量计算出粘结剪切刚度系数,具体公式为
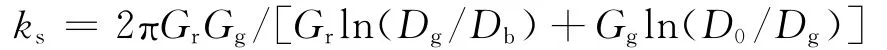
式中:Gr、Gg分别为岩石及砂浆的剪切模量;Db、Dg、D0分别为锚杆直径、注浆圈外直径及影响当量直径.
根据Li的思想,针对本文的模拟情况,对砂浆体的粘结剪切刚度系数做了下列求解.假设砂浆层的厚度B=rg-rb,根据砂浆层内静力平衡,剪应力分布为

其对应的剪应变沿径向非均匀分布,与离锚杆中心的距离成反比,则距锚杆 -砂浆截面距离为b处的砂浆剪应变为

对上式积分,得到砂浆层的总剪应变,即砂浆与锚杆相对位移:

因此,粘结剪切刚度系数可以表示为

该计算公式可视为只考虑砂浆层变形的特殊情形.
2 数值模拟
为深入研究全长粘结锚杆最大拉拔荷载与砂浆粘结破坏的关系,对锚杆-砂浆界面进行有限元数值模拟,分析不同拉拔荷载作用下界面的受力情况.
2.1 计算假定
本文采用有限元软件ABAQUS进行数值模拟,在算例中,采用了以下一些假定:
(1)计算区域内岩体为均质、连续、各向同性材料;
(2)锚杆材料取为光圆钢筋,保证在拉拔过程中只出现注浆体的剪切破坏,而未出现注浆体的径向破坏;
(3)锚杆视为线弹性材料,在最大拉拔荷载之前未进入塑性阶段;
(4)整个过程未考虑预应力的影响.
2.2 计算模型
取高、宽为20倍锚杆直径,长为1.5倍锚杆长度的长方体岩体作为研究对象进行分析.建模分析中,岩体采用三维八节点实体单元C3D8R,锚杆采用空间梁单元B31.目前,对于粘结及粘结破坏界面均可采用弹簧单元,即在界面设置若干弹簧模型,通过对弹簧刚度的调整,来达到模拟真实界面的目的,即在粘结界面破坏之后,弹簧单元还可以提供不随相对位移变化的残余剪应力.计算模型见图4.

图4 ABAQUS计算模型Fig.4 Computational model in ABAQUS
2.3 模型参数
根据上述理论分析及参考以往试验结果,模型材料参数按照表1数据选取(数据参考典型硬岩试验参数).根据上文理论,可以推导出界面剪应力与锚杆-砂浆相对位移的定量关系,如图5所示.加载初期,界面剪应力与相对位移成简单线性关系,此时设置初始弹簧刚度为常数,能较好地模拟该线性受力段;随着位移增加,界面开始出现破坏,剪切刚度逐渐下降,此时设置刚度逐渐减小的非线性弹簧作该过渡软化段的模拟;最终,界面粘结完全破坏,粘结力由摩阻力取代,此后,弹簧强度不再随位移变化.由上述分析,模型中弹簧单元参数可按图示关系选取.

表1 拉拔试验参数Tab.1 The parameters of pull-out test

图5 界面剪应力与锚杆-砂浆相对位移的关系Fig.5 Relationship between interface shear stress and bolt-grout relative displacement
3 计算结果及分析
3.1 锚杆破坏过程分析
如图6所示,加载初期,锚杆所受拉拔荷载F随端部位移u增大而增大,在未出现界面破坏之前,荷载与位移成线性关系;随着拉拔荷载增大,端部位移依然很小,端部界面剪应力已经超过最大容许剪应力,此时锚杆出现破坏段,拉拔荷载呈现非线性增长,且增速变小,说明破坏段一直增长,剪应力峰值向锚固深部移动;当拉拔荷载达到某一数值后迅速下降,表明该数值为最大拉拔荷载,结果证明界面平均粘结力概念的意义不是很大,界面粘结力和摩阻力的最优分布决定了最大拉拔荷载的大小.

图6 锚杆端部位移与拉拔力的关系Fig.6 Relationship between pull-out load and bolt end displacement
3.2 锚杆几何参数对最大拉拔荷载的影响
一般地,影响锚杆最大拉拔荷载的主要因素有锚杆直径、锚杆长度和锚固剂性能.图7和8表示的是锚杆最大拉拔荷载与锚杆几何参数的关系:在最长锚固深度范围内,不同直径和长度的锚杆剪应力分布函数形式基本相同,因此在锚杆长度相同的情况下,最大拉拔荷载与锚杆直径成线性关系;在锚杆直径相同的情况下,最大拉拔荷载与锚杆长度成线性关系.锚杆直径和长度的增大均增加了锚杆在岩体中的锚固面积,可以有效地改善锚杆的锚固效果,使锚杆的作用范围增大,进而提高了锚杆的拉拔荷载,与以往的试验结果[12]较为吻合.同时,锚杆的最大拉拔荷载除受界面粘结力和摩阻力的影响,也会受到锚杆材料极限拉伸强度的限制,因此并不会无限增加.
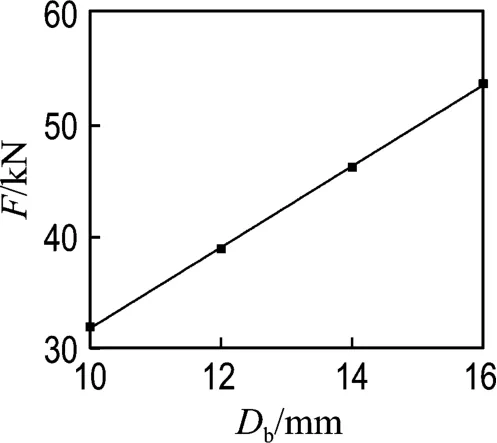
图7 锚杆最大拉拔荷载与直径的关系Fig.7 Relationship between the largest pull-out load and bolt diameter

图8 锚杆最大拉拔荷载与锚固长度的关系Fig.8 Relationship between the largest pull-out load and bolt length
3.3 砂浆剪切模量对最大拉拔荷载的影响
由于砂浆层的剪切模量决定界面粘结剪切强度,而砂浆层的抗剪强度决定界面最大剪应力,两者的非线性关系也决定了最大拉拔荷载和砂浆剪切模量的非线性关系(图9).一般地,砂浆层的剪切模量对锚杆最大拉拔荷载会有明显的影响,因为其大小决定界面粘结剪切刚度的大小,而界面粘结剪切刚度的增大增加了围岩体对锚杆的作用力,从而对最大拉拔荷载产生影响.数据拟合后,最大拉拔荷载与剪切模量成近似对数关系,同样与以往的试验结果[12]较为吻合.

图9 锚杆最大拉拔荷载与砂浆剪切模量的关系Fig.9 Relationship between the largest pull-out load and grout shear modulus
4 结 论
(1)全长注浆锚杆拉拔过程中,沿全长出现不同的受力分布,并随端部位移的增大而进一步发生性状的变化;在达到最大拉拔荷载时,受力分布最优,锚固体提供最大的拉拔承载力.
(2)数值结果表明多种因素通过改变砂浆层的尺寸和强度对锚杆最大拉拔荷载产生影响.在最长锚固深度范围内,最大拉拔荷载与锚杆的直径和长度成近似线性关系;与砂浆剪切模量成近似对数关系;但最大拉拔荷载会受到锚杆材料强度的限制,并不会无限增大.
(3)本文采用的弹簧模型可以完整地表示界面破坏前后剪应力的变化情况,较好地模拟锚杆不同区段(弹性段、软化段及破坏段)内的破坏机制和力学特性,对以后的锚杆拉拔研究会有很好的借鉴意义.
[1]张乐文,汪 稔.岩土锚固理论研究之现状[J].岩土力学,2000,23(5):627-631.ZHANG Le-wen,WANG Ren.Research on status quo of anchorage theory of rock and soil[J].Rock and Soil Mechanics,2000,23(5):627-631.(in Chinese)
[2]高永涛,吴顺川,孙金海.预应力锚杆锚固段应力分布规律及应用[J].北京科技大学学报,2002,24(4):387-390.GAO Yong-tao,WU Shun-chuan,SUN Jin-hai.Application of the pre-stress bolt stress distributing principle[J].Journal of University of Science and Technology Beijing,2002,24(4):387-390.(in Chinese)
[3]Phillips S H E.Factors Affecting the Design of Anchorages in Rock [M].London:Cementation Research Ltd.,1970.
[4]尤春安.全长粘结式锚杆的受力分析[J].岩石力学与工程学报,2000,19(3):339-341.YOU Chun-an.Analysis on bolt strain with large deformation under shearing-tensile load[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(3):339-341.(in Chinese)
[5]杨 庆,朱训国,栾茂田.全长注浆岩石锚杆双曲线模型的建立及锚固效应的参数分析[J].岩石力学与工程学报,2007,26(4):692-698.YANG Qing,ZHU Xun-guo,LUAN Mao-tian.Development of hyperbolic model for fully grouting rock bolt and parameters analysis for anchoring effect[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(4):692-698.(in Chinese)
[6]张季如,唐保付.锚杆荷载传递机理分析的双曲函数模型[J].岩土工程学报,2002,24(2):188-192.ZHANG Ji-ru,TANG Bao-fu.Hyperbolic function model to analyze load transfer mechanism on bolts[J].Chinese Journal of Geotechnical Engineering,2002,24(2):188-192.(in Chinese)
[7]刘建庄,张 农,韩昌良.弹性拉拔中锚杆轴力和剪力分布力学计算[J].中国矿业大学学报,2012,41(3):344-348.LIU Jian-zhuang,ZHANG Nong,HAN Changliang.Elastic stress distributions:axial and shear stress distributions in an anchor bolt during a pullout test [J].Journal of China University of Mining & Technology,2012,41(3):344-348.(in Chinese)
[8]Farmer I W.Stress distribution along a resin grouted rock anchor [J].International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstract,1975,12(11):347-351.
[9]庄 茁,朱万旭,彭文轩,等.预应力结构锚固-接触力学与工程[M].北京:科学出版社,2005.ZHUANG Zhuo,ZHU Wan-xu,PENG Wen-xuan,etal.Anchorage-contact of Pre-stressed Structure in Mechanics and Engineering [M].Beijing:Science Press,2005.(in Chinese)
[10]韩 军,陈 强,刘元坤,等.锚杆灌浆体与岩(土)体间的粘结强度[J].岩石力学与工程学报,2005,24(19):3482-3486.HAN Jun,CHEN Qiang,LIU Yuan-kun,etal.Bond strength between anchor grout and rock or soil masses[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24 (19):3482-3486. (in Chinese)
[11]Li C,Stillborg B.Analytical models for rock bolts[J].International Journal of Rock Mechanics and Mining Science,1999,36(8):1013-1029.
[12]Kilic A,Yasar E,Celik A G.Effect of grout properties on the pull-out load capacity of fully grouted rock bolt[J].Tunneling and Underground Space Technology,2002,17(4):355-362.

