基于SiPESC.OPT的结构动力模型修正研究

杨 春 峰， 路 林 华， 张 盛＊， 李 云 鹏， 陈 飙 松

（1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.大连理工大学 运载工程与力学学部 工程力学系，辽宁 大连 116024）

0 引 言

模型修正（model updating）技术旨在获得一个能够重现所有实验测得的模态参数的有限元模型，或者是获得一个能够重现所有测得的频率响应函数的模型.

有限元模型（理论模型）计算中最主要的问题是精度问题.Mottershead等［1］把有限元模型的误差主要归结为以下三方面：一是有限元模型的结构误差，这种误差通常是由有限元建模过程中的线性化假设以及边界条件的近似引起的；二是模型的阶次误差，这是指有限元方法将实际连续的无限维模型离散为有限维模型所带来的误差，离散后的有限元模型的自由度数有限而无法模拟出无限自由度的真实结构；三是模型的参数误差，这种误差主要由对初始模型不精确的简化、近似以及环境变化和生产制作等原因造成材料和几何参数的不确定引起的.

结构动力模型修正兴起于20世纪70年代，常用方法有矩阵型修正法、参数型修正法、基于神经网络算法的修正方法、基于优化设计的修正方法等.

将模型修正问题转化为优化问题来处理是参数型模型修正方法中比较常见的一种方法.刘继承等［2］基于一阶优化算法，只需利用结构模态试验的部分固有频率，就能获得较精确的有限元模型.郭彤等［3］采用基于特征灵敏度的优化设计方法对润扬长江大桥斜拉桥进行了模型修正，分析结果为大跨桥梁的结构损伤识别和安全监测工作提供了一定的依据.郑惠强等［4］利用Ansys中的优化功能对TL50型桥吊结构进行了模型修正，为之后的结构瞬态动力学分析提供了切合实际的数学模型.

本文首先阐述将参数型模型修正方法转化为优化问题来求解的基本思路，然后通过桁架和Garteur算例来验证该方法的可行性，并详细分析介绍基于优化的模型修正方法中模型精化、修正参数选择、取值范围调整等问题.

1 参数型模型修正方法

Mottershead等认为理论模型的不精确主要一个原因便是有限元模型的参数误差.这种误差主要由对初始模型不精确的简化、近似以及环境变化和生产制作等原因造成材料和几何参数的不确定引起的.进一步考虑，将这种误差定位为有限元模型中各个单元的误差共同作用引起的［5－7］.假设实验模型和有限元计算模型存在着以下关系：

式中：Kn、Mn分别为有限元模型第n个单元的刚度矩阵、质量矩阵对系统整体矩阵的贡献；K＊、M＊分别为实验测试模型对应的刚度矩阵、质量矩阵；Ne表示有限元模型单元的个数；ΔKn、ΔMn分别是有限元模型和实验模型之间的第n个单元的补偿刚度阵、补偿质量阵，其参数αn、βn为第n个单元的刚度修正参数、质量修正参数，可以是单元的弹性模量、密度，或者是其他量.

由式（1）可以看出，每一个单元的刚度阵和质量阵分别只有一个修正参数，有时候可能无法准确地描述单元的误差.于是对式（1）进行改造可得［6］

式中：αnk表示第n个单元的补偿刚度阵的第k个修正参数，βnk表示第n个单元的补偿质量阵的第k个修正参数.

将模型修正问题转化为一个以αnk、βnk为参数的优化问题：

其中L、U分别指参数的下、上限.目标函数f设定为动力分析结果的函数，如频率相关性函数、模态相关性函数.本文以频率相关性函数

为优化目标函数.其中ωi为有限元分析的第i阶频率为实验所测得的第i阶频率.根据对不同频率的重要性，对上式进行改造，于是其中αi为第i阶频率相关性的权重因子，其值越大，该阶频率对优化目标的影响越大，修正后该阶频率的精度也会越高.

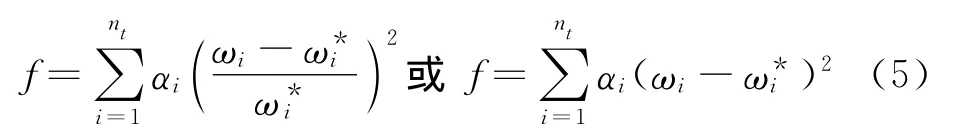
模型修正的关键工作之一是选择修正参数.面向具体问题，应根据有限元模型力学特性、优化目标、试验结果等因素选取合适的模型参数，甚至可以说模型参数的选择是成败的关键.一般而言，有限元模型的连接刚度、主要部件的刚度／质量、部件几何参数都可能是被选参数.

2 基于SiPESC.OPT的模型修正方法的实现

SiPESC.OPT［8］是大连理工大学工程力学系自主研发的一个开放的通用优化问题求解软件，用于求解单目标或多目标、连续设计变量和离散设计变量、线性或非线性的大规模复杂优化问题.SiPESC.OPT包含有试验设计、近似模型模拟、灵敏度分析、子系统集成、文本文件解析等多种先进功能模块.它包含BFGS、SLP、SQP、GA等多种业界公认的成熟优化算法；提供均匀试验设计、正交试验设计、中心复合试验设计、析因试验设计等试验设计方法；响应面法、多二次径向基函数、高斯径向基函数、逆多二次径向基函数等近似模型拟合方法.该软件一个特色功能是支持脚本语言（JavaScript）功能，可通过脚本集成外部软件（如结构有限元分析软件），完成复杂问题的集成计算与优化.

通过编写SiPESC.OPT的脚本文件，实现了优化算法和商用软件的集成.其优化流程如图1所示，所有的环节都是在脚本的控制下进行的.

图1 模型修正流程图Fig.1 Flow chart of model updating

主要步骤1 集成计算软件.调用有限元软件，如Ansys，读取参数化模型文件进行建模分析计算并生成结果文件，脚本代码如下：

var programe＝″＼″C：／Program Files／ANSYS Inc／v121／ansys／bin／intel／ansys 121.exe＼″－b－i E：／ansys／GARTEUR（4）／3stepGarteur.txt－o output.txt－dir e：／ansys／GARTEUR（4）″

process＝new Process；

process.execute（programe）；

3stepGarteur.txt为Ansys参数化模型文件，其中采用了APDL参数建模功能.针对不同的商用软件集成，均可参照上述步骤进行，只需进行脚本代码的修改即可.

主要步骤2 导入结果及修改计算参数.通过脚本语言读取有限元分析结果，以及修改计算参数，实现商业软件计算的输入输出的控制.文件和修改修正参数的脚本代码如下：

parser＝new FileParser；

parser.open（″E：／ansys／GARTEUR（4）／modefile＿ansys.txt″）；

var obj1＝parseFloat（parser.retrieveString（760，774））；

var link2H＝ theModel.getVariable（″link2H″）；

parser＝new FileParser；

parser.open（″E：／ansys／GARTEUR（4）／3stepGarteur.txt″）；

parser.replaceString（103，111，link2H）；

parser.close（）；

其中 modefile＿ansys.txt为结果文件，obj1为结果文件中的某阶频率，link2H为参数化模型文件中的一个修正参数.

主要步骤3 设置优化算法.如本文采用的GA（遗传）算法，其设置如下：

GA.setMINMAX（－1）；

GA.setGENERATION（200）；

GA.setPOPULATIONSIZE（60）；

GA.setMUTATIONPROBABILITY（0.1）；

GA.setCROSSOVERPROBABILITY（0.8）；

var Solver＝ GA ；

若需选择其他算法，只需修改这部分代码即可.

3 基于优化的模型修正算例

按照上述方法，本文完成了桁架结构和Garteur飞机模型两个模型修正算例.前者主要是用来验证基于SiPESC.OPT的结构动力模型修正方法的可行性，后者则进一步分析研究了模型修正中模型精化、参数选择、灵敏度分析等过程.

3.1 桁架算例

如图2所示，该桁架结构有8个节点，13个单元.其中1、8号节点固定.横截面积均为5.0×10－5m2，弹性模量为20.7GPa，目标密度为7.8×103kg／m3，泊松比为0.3，垂直和水平方向的杆长2m.

图2 桁架结构图Fig.2 Truss structure

图3 部分脚本代码Fig.3 Part of script code

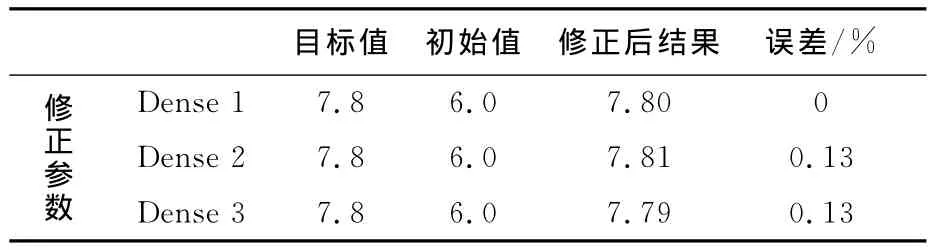
表1 桁架修正结果Tab.1 Updating result of truss structure

结果表明，当优化目标值收敛以后，修正参数的修正结果与目标值的平均误差降为了0.087%，很好地完成了对有限元计算模型的修正，说明将模型修正问题转化为优化问题来处理是一种可行的方法，其中关键的环节是提取正确的优化模型.

3.2 Garteur飞机模型算例

Garteur［9］飞机模型是具有12个成员的欧洲航空科技研究组织结构与材料工作组建立的一个典型的标准飞机模型，如图4、5所示.该模型具有真实飞机高柔度、模态频率低且密集的特点，宽2.0m，长1.5m，由硬质铝材通过螺栓连接而成，目前已经被该组织设为评估模型修正技术与实验分析技术的基准模型.国内外很多学者和单位也对此模型进行了大量的实验分析，并以此展开模型修正的研究.G ge等［10］把误差定位为机身与机翼连接处、机身与尾翼连接处，并以此为重点对模型进行修正.丁继锋等［11］提出了模型修正的三步策略，并对Garteur飞机模型进行修正，取得了很好的精度.王彬文等［12］对Garteur飞机模型进行实验，结合修正参数运用参数优化的手段修正了有限元模型，使仿真结果和实验结果取得很好的一致性.李伟明［5］根据经验选取了建模中材料参数不确定的5个连接部位及其附近部位共26个单元作为待修正单元，将每个单元的弹性模量和密度作为修正参数对模型进行修正.

一般Garteur飞机修正算例中都采用弹簧单元和刚性单元来模拟飞机模型的螺栓连接部分，本文用弹性体单元来模拟模型中的连接部分.修正过程中考虑了实验温度对模型材料的影响以及螺栓连接的特殊性，采用循序渐进的方法逐步精化和修正有限元模型.

将Garteur飞机模型算例分为三步来进行.第一步针对简化的有限元模型进行修正，初步定位有限元模型误差产生的原因.第二步是在第一步修正信息的基础上，建立精细的有限元模型，增加新的修正参数，调整修正参数的取值范围，然后对模型进行修正.第三步考虑到过多的修正变量不仅会降低模型修正的效率，还会影响优化算法本身对全局最优解的逼近，于是通过灵敏度分析进一步缩减参与修正的变量，并且在考虑螺栓连接特殊性的基础上进一步调整部分修正变量的取值范围.

3.2.1 Garteur飞机简化模型的修正 首先通过Ansys建立Garteur飞机简化的有限元模型，采用弹性体单元来模拟Garteur飞机的连接处，如图5所示.整个模型可以分为6部分：机身、水平机翼和4处连接.

图4 Garteur飞机模型Fig.4 Garteur plane model

图5 简化模型及其连接处Fig.5 Simplified model and details connections

Garteur飞机模型是由铝合金板在螺栓的作用下连接生成的.铝合金板的密度和弹性模量会因实验温度和规格的不同而不同，故将其列为修正变量.模型连接处是由螺栓和铝板共同组成的，在有限元中由弹性体单元来模拟，此处的误差是整体误差中最重要的一部分，故将其也列为修正变量.由于无法确认其精确的修正范围，在初步修正中所有的修正变量都定义在一个很大的范围内，密度的取值范围为1.0×103～5.0×103kg／m3，弹性模量的取值范围为10～500GPa.以作为目标函数，其中ωi表示有限元分析中的第i阶频率表示西悉尼大学（UWS）实验结果［12］中的第i阶频率.采用遗传算法对模型进行修正，修正结果如表2所示.

由表2可以发现，修正后的有限元模型的计算结果和实验结果的平均误差为3.52%.该模型不足以进一步提高结果的精准度，必须在此基础上进一步精化有限元模型.

表2 简化模型的修正结果Tab.2 Updating results of simplified model

3.2.2 Garteur精化模型的修正 在简化模型进行修正和结果分析的基础上进一步精化有限元模型，将机身机翼连接处分成了上中下三部分，将机身尾翼连接处分成了前后两部分，尾翼上方连接处分成了上下两部分，如图6所示.整个模型可以分为10部分，把每一部分的弹性模量和密度作为模型修正参数.

图6 精化Garteur模型及其连接处Fig.6 Fine Garteur model and details connections

铝合金板和螺栓的密度及弹性模量会因实验温度和规格的不同而不同.铝合金板其密度大多分布在2.5×103～3.0×103kg／m3，其弹性模量大多分布在65～75GPa.钢质螺栓的密度大多分布在7.5×103～8.0×103kg／m3，弹性模量分布在190～220GPa.以此为参考重新调整修正变量的取值范围：模型连接处体单元密度的取值范围定为2.5×103～10.0×103kg／m3，弹性模量下限定为70GPa；模型非连接处体单元的密度取值范围定为2.5×103～3.0×103kg／m3，弹性模量的取值范围为 65～75GPa.以 mino＝作为目标函数，采用遗传算法对模型进行修正，修正结果如表3所示，平均误差为2.58%.

表3 精化模型的修正结果Tab.3 Updating results of fine model

3.2.3 调整修正参数及其取值范围 如前文所述，模型修正是数学上的反问题.过多的修正参数不仅会大幅度地降低模型修正效率，而且还会增加模型陷入局部最优解的可能性.为了去除不必要的修正参数，在精化模型修正结果的基础上对各修正参数进行灵敏度分析，判别各参数对模型动力分析结果的影响.去除对动力分析结果几乎没有影响的修正参数；去除模型中每一部分的密度参数，其数值沿用第二步的修正结果.对模型各部分的弹性模量进行灵敏度分析，各修正参数及其对模型动力分析结果的影响如表4所示.由于第一阶频率误差较大，并且其相关参数仅仅有水平机翼的弹性模量一个，为了避免出现现有参数不足以描述第一阶频率误差的情况，增加机身机翼连接处上部的水平尺寸为修正参数.由于尾翼上方连接处上部分的弹性模量和尾翼上方连接处下部分的弹性模量对动力分析结果几乎没有影响，去除这两个修正参数.

表4 各修正参数对动力分析结果的影响Tab.4 The impact of updated parameters on dynamic analysis results

由于螺栓连接比较特殊，在有限元中属于非线性问题，本文采用弹性体单元来模拟螺栓连接，其弹性模量会有较大浮动范围，因此螺栓连接处的弹性模量的取值范围应为10～500GPa，以作为目标函数，采用遗传算法对模型进行修正.修正结果如表5所示.由表可以看出，作为目标值的1到9阶频率的平均误差为1.18%，仅有两阶频率的误差超过了1.00%，精度非常高.

为了进一步评估模型修正结果的质量，取有限元中不参与目标修正的第10～14阶频率与实验结果中的第10～14阶频率进行比较，如表6所示.其平均误差为2.20%，符合修正要求.

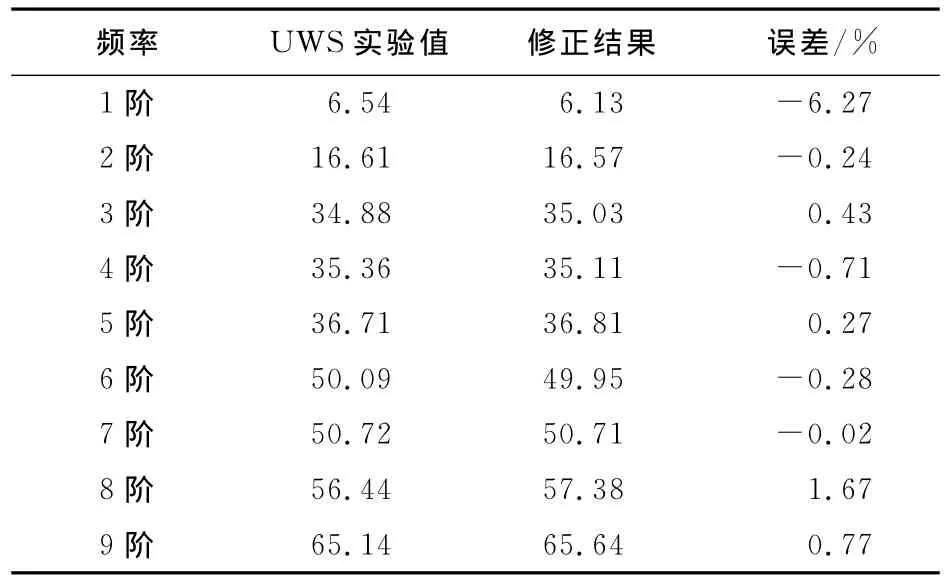
表5 新修正参数的修正结果Tab.5 Results based on new updated parameters

表6 未参与修正的各阶频率Tab.6 Independent frequencies

4 结 论

本文基于自主优化软件SiPESC.OPT，通过集成结构有限元分析软件，进行了结构动力模型修正问题研究.主要思路是将模型修正问题转化为优化问题，通过提取有效合理的优化模型完成对有限元模型的修正.桁架和Garteur飞机的修正算例很好地验证了该方法的可行性以及工程实用价值.

研究工作表明模型修正问题是数学上的反问题，修正过程中的不同设定，如修正参数的不同、目标函数的不同、参数范围的不同，都可能导致不同的修正结果.只有准确定位误差产生的原因，并提取正确的参数，严格控制其取值范围，结合高性能高精度的优化算法才能得出质量较高的修正结果.

［1］Mottershead J E，Friswell M I.Model updating in structural dynamics：A survey［J］.Journal of Sound and Vibration，1993，167（2）：347－375.

［2］刘继承，周传荣.一个基于优化的有限元模型修正方法［J］.振动与冲击，2003，22（2）：33－35.LIU Ji－cheng，ZHOU Chuan－rong.FE model updating method based on optimization［J］.Journal of Vibration and Shock，2003，22（2）：33－35.（in Chinese）

［3］郭 彤，李爱群，韩大章.基于灵敏度分析与优化设计原理的大跨桥梁动力模型修正［J］.桥梁建设，2004（6）：20－23.GUO Tong，LI Ai－qun，HAN Da－zhang.Updating of dynamic model for long－span bridges based on structural sensitivity analysis and optimization design principle［J］.Bridge Construction，2004（6）：20－23.（in Chinese）

［4］郑惠强，陈鹏程，宓为建，等.大型桥吊结构动力有限元模型修正［J］.同济大学学报，2001，29（12）：1412－1415.ZHENG Hui－qiang，CHEN Peng－cheng，MI Weijian，etal.Dynamic model updating of the port crane ［J］.Journal of Tongji University，2001，29（12）：1412－1415.（in Chinese）

［5］李伟明.有限元模型修正方法及自由度匹配迭代技术研究［D］.上海：上海交通大学，2011：125－136.LI Wei－ming.Study on finite element model updating method and iterative technique for degree of freedom matching ［D］.Shanghai：ShanghaiJiaotong University，2011：125－136.（in Chinese）

［6］Farhat C，Hemez F M.Updating finite element dynamic models using an element－by－element sensitivity methodology ［J］.AIAA Journal，1993，31（9）：1702－1711.

［7］Hu S L J，Li H J.Simultaneous mass，damping，and stiffness updating for dynamic systems ［J］.AIAA Journal，2007，45（10）：2529－2537.

［8］杨春峰，陈飙松，张 盛，等.通用集成优化软件系统SiPESC.OPT的设计与实现［J］.计算机辅助工程，2011，20（4）：42－48.YANG Chun－feng，CHEN Biao－song，ZHANG Sheng，etal.Design and implementation of general integrated optimization design software SiPESC.OPT ［J］.Computer Aided Engineering，2011，20（4）：42－48.（in Chinese）

［9］Link M， Friswell M I.Working group 1：Generation of validated structural dynamic modelsresults of a benchmark study utilising the GARTEUR SM－AG19test－bed ［J］.Mechanical Systems and Signal Processing，2003，17（1）：9－20.

［10］G ge D，Link M.Assessment of computational model updating procedures with regard to model validation ［J］.Aerospace Science and Technology，2003，7（1）：47－61.

［11］丁继锋，马兴瑞，韩增尧，等.结构动力学模型修正的三步策略及其实践［J］.航空学报，2010，31（3）：546－552.DING Ji－feng， MA Xing－rui， HAN Zeng－yao，etal.Three－step model updating method in structure dynamics and its application ［J］.Acta Aeronautica Et Astronautica Sinica，2010，31（3）：546－552.（in Chinese）

［12］王彬文，杨文岐，苟小宜，等.GARTEUR飞机模型振动特性研究［J］.振动工程学报，2008，21（S）：179－182.WANG Bin－wen，YANG Wen－qi，GOU Xiao－yi，etal.Vibration character research of GARTEUR aircraft model ［J］.Journal of Vibration Engineering，2008，21（S）：179－182.（in Chinese）