混凝土试样单轴压缩端面效应及破坏数值模拟

陈 健 云， 刘 智 光＊，2

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；2.长沙理工大学 水利工程学院，湖南 长沙 410004)

0 引 言

单轴压缩试验是研究混凝土受压变形、开裂及破坏过程(包括峰值应力后的应变软化性能)的基本试验，得到的应力－应变全曲线反映了材料强度和变形性能，已经列入了结构设计规范[1].但是试验结果受很多因素影响，如试样几何形状和尺寸、试验机刚度、加载端头与试样间的摩擦条件等，不加区分地依靠大量试验数据的回归，希望得到材料的“本构”性质显然是不现实的.RILEM曾组织欧美多国实验室开展“混凝土应变软化试验方法”的研究，着重分析了加载端头约束条件和试样长细比对试样强度、应变软化和破坏形态等宏观力学性能的影响[2－3].不同试验条件下混凝土的宏观力学性能与材料内部裂纹发展相关.近年来出现的细观数值分析方法，考虑细观层次的材料非均质性，用数值模拟研究混凝土材料的断裂过程与宏观性能劣化之间的关系，为研究不同条件下试样的应力、应变分布和微裂纹萌生、扩展、成核的破坏过程提供了有效途径[4－5].

按照混凝土细观结构的离散方式，目前在细观数值分析中应用较多的模型有格构模型[4，6]、粒子模型[7]和连续细观模型[8－9].细观层次上一般将混凝土视为由骨料、砂浆基质和界面过渡区组成的三相材料，如果直接从界面过渡区尺寸量级(厚度仅为0.01～0.10mm)对混凝土进行离散，将使问题的规模过于庞大.因此，细观数值模型中往往采取如下3种简化处理方式:增大界面过渡区厚度以适应网格剖分、将界面过渡区单独设置为无厚度单元，以及将界面过渡区和砂浆基质以串联的形式考虑.但是它们都改变了界面过渡区的几何特征，作者最近发展的复合型界面损伤模型对此进行了改进[10－11].本文应用该模型，数值模拟不同端面约束条件下混凝土立方体试样的轴压破坏过程.

1 细观数值模型简介

本文采用的复合型界面损伤模型，以常规有限元单元离散混凝土细观结构，具体包括如下几方面的内容:产生三相结构的细观数值试样；采用Weibull分布随机生成细观单元中组成材料的力学性能参数[9]，将混凝土细观力学性能的非均匀性引入数值模型；采用复合材料力学中的匀质化技巧，确定由界面过渡区和与之相邻的骨料及砂浆基质组成的等效均质区域的材料力学性能；计算等效均质区域材料的损伤.

如图1所示，混凝土的细观结构通过单元的材料信息表达.参照将Fuller骨料三维级配问题转化到平面的 Walraven公式[12]，采用蒙特卡罗方法，产生二维骨料结构，假设骨料镶嵌在砂浆基质中，界面过渡区位于骨料表面.将规则化有限元网格覆盖到此细观结构上，得到完全由骨料或砂浆基质组成的单一材料单元，和包含界面过渡区及与之相邻的骨料和砂浆基质的复合材料单元(图1(c))，文中称为内嵌界面单元.

图1 混凝土随机骨料结构、规则化有限元网格与细观单元Fig.1 Random aggregate structure，regular FE mesh and meso－element

应用复合材料力学中的修正Voigt－Reuss模型[13]，确定由骨料、砂浆基质和界面过渡区组成的内嵌界面单元的平均材料性质.此外，根据修正Voigt－Reuss模型，若已知内嵌界面单元的平均应力与平均应变，可计算各组成材料的局部应力和应变，这将在确定内嵌界面单元的损伤时用到.

内嵌界面单元的损伤通过其组成材料的损伤体现.以拉断的Mohr－Coulomb准则作为材料的损伤判据，拉伸损伤具有优先权，损伤演化模型依弹性损伤本构关系描述，且各组成材料的损伤演化模型是一致的.内嵌界面单元的损伤计算可按如下方式进行:由单元的应力和应变计算各组成材料的应力和应变，然后计算各组成材料的损伤，单元的损伤通过复合本构矩阵的弱化体现.为避免问题的复杂性，假设内嵌界面材料单元内各组成材料的损伤是各向同性的，但是损伤后的单元显然是各向异性的.

对于只含骨料和砂浆基质的单一材料单元也采用同样的损伤演化模型.不同的是，单元剪切损伤是各向同性的，若发生拉伸损伤则考虑单元的正交各向异性损伤.

有关复合型界面损伤模型的详细介绍参见文献[9－11].本文采用该模型研究了端面约束条件对混凝土立方体试样轴压破坏过程的影响.

2 考虑端面效应的轴压破坏数值模拟

考虑平面应力问题，混凝土试样尺寸为100 mm×100mm，界面厚度暂取0.1mm，最大骨料粒径为10mm，骨料填充率为45%，以边长为1mm的正方形单元规则剖分试样.这里考虑C45混凝土，立方体抗拉、抗压强度标准值分别为2.51、29.60MPa，弹性模量为33.5GPa[1].唐春安等[9]通过大量的工作，给出了混凝土三相材料参数Weibull分布的数值配比方案.基于此，本文生成混凝土数值试样的参数取值如表1所示.骨料、砂浆基质和界面材料的泊松比相对均匀，其值分别为0.18、0.20和0.25；摩擦角均为30°，压缩残余强度系数均为0.05，单轴抗拉强度均为单轴抗压强度的1／15.在试样上端面采用位移加载，加载步长为0.5μm.对于光滑端面条件，仅在试样下端面节点施加法向约束；对于粗糙端面条件，除了在下端面施加法向约束，试样上、下端面还施加侧向约束.

表1 混凝土试件的 Weibull分布力学参数Tab.1 Mechanical parameters of Weibull distribution of concrete specimens

2.1 端面约束条件对试样强度和变形特征的影响

2.1.1 应力－轴向应变曲线 图2为模拟得到的应力－轴向应变全曲线，与van Vliet等[3]的试验结果较符合，曲线形状和峰值应力等受到端面约束条件的影响.从图中可以看出，粗糙端面条件下试样的峰值应力(σ0)高于光滑端面，依据数值结果，粗糙端面的峰值应力为41.8MPa，光滑端面为30.5MPa；与峰值应力对应的峰值应变(ε0)也有此规律；若取30%峰值应力处的割线模量为试样的弹性模量，两种端面条件下大致相等，文中试样为33.0～34.0GPa.这与文献[3]通过试验得到的结论一致.该文还指出，和端面光滑相比，端面粗糙条件下应力－应变曲线峰后软化段的延性更强，也与本文数值模拟结果互为佐证.

图2 不同端面约束的试样应力－轴向应变曲线Fig.2 Stress－axial strain curves for specimen loaded under different boundary conditions

如果加载端面粗糙，因为试验机加载端头的约束，端部混凝土的侧向变形(垂直于加载方向)受到限制，而且离加载端头距离越近限制性越强.在一定端部区域内的混凝土处于双轴受压状态，相比于其他区域侧向受拉的混凝土，损伤和微裂纹的发展也受到限制.也就是说，不能像在光滑端面条件下一样，损伤和微裂纹可自由地发生在试样最薄弱位置，而被迫在侧向变形不受限制或限制较弱的区域发生.因此，端面粗糙时试样的破坏需要在更高的外荷载水平下进行，消耗更多的能量，要求应力－轴向应变曲线所围面积比端面光滑的更大，图2的数值结果证明了这一点.

2.1.2 应力－侧向应变曲线 试样侧向应变按如下方式确定[4]:取试样1／2高度处的节点，将节点的侧向位移(ux)作为侧向坐标(x)的函数并绘于坐标系中，线性回归线斜率即为试样的宏观侧向应变.

图3为应力－侧向应变曲线，正如所见:

(1)从开始加载直至70%～80%峰值应力，不论端面约束条件如何，侧向应变与轴向应变成比例增加；之后侧向应变增加更快，峰值应力后尤为明显，在软化段清晰地表明试样侧向应变将超过轴向应变.

(2)相比于光滑端面，加载端面粗糙条件下峰值应力对应的侧向应变较大.

(3)在峰后软化段，光滑端面的应力下降至88%峰值应力时横向应变即已超过轴向应变，而粗糙端面下降至76%峰值应力才出现这一现象，表明在峰后软化段光滑端面条件下试样的横向应变增加更快.

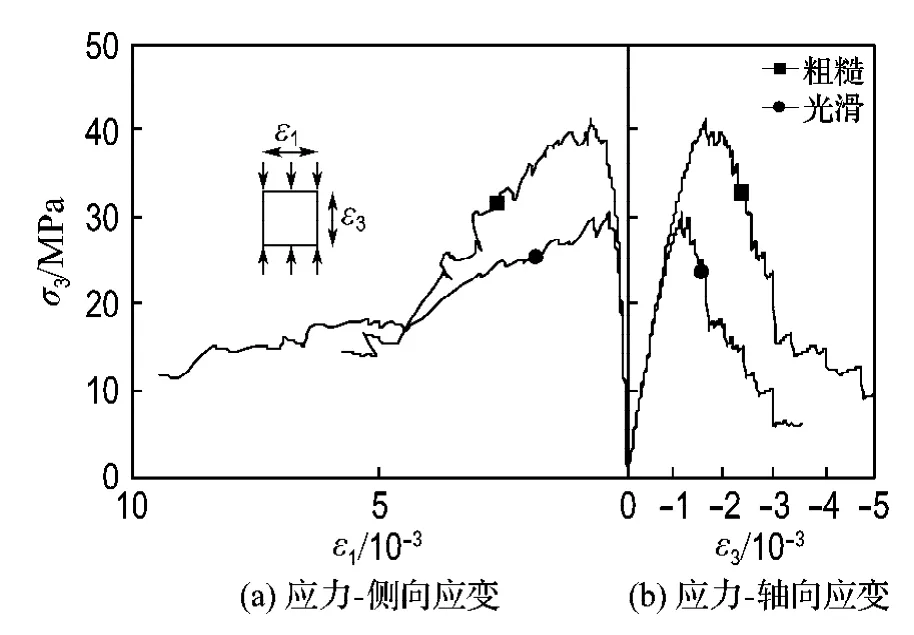
图3 不同端面约束的试样应力－轴向应变曲线和应力－侧向应变曲线Fig.3 Stress－axial strain curves and stress－lateral strain curves for specimen loaded under different boundary conditions

如果端面光滑，试样发生劈裂破坏(见后文对破坏过程的分析)，可将侧向变形过程分为两个阶段.第一阶段包括侧向应变与纵向应变成比例增长的初始加载阶段和少量局部裂纹贯通的峰值应力附近(已处于峰后软化段，但是宏观劈裂裂纹尚未完全形成)，侧向应变的增加是平缓的.在第二阶段，由于宏观劈裂裂纹临近形成或已经形成，试样的侧向应变迅速增加.

若端面粗糙，试样的侧向变形受到限制，而且从试样端部到试样高度的中央，限制是逐步减弱的，所以试样高度的中央侧向变形最大.另外，虽然在轴向压缩过程中，侧向应变的增加速度是越来越快的，但是除了在破坏严重、表层混凝土甚至剥落的残余强度阶段，侧向应变的增加相对平缓，并不会出现如光滑端面条件下迅速增加的情形.

2.1.3 应力／峰值应力(σ3／σ0)与泊松比的关系图4给出了由轴向应变与侧向应变计算得到的峰值应力前的试样泊松比变化曲线.

开始加载时不同端面约束条件的泊松比相差很小.光滑端面条件下，直至逼近80%峰值应力，泊松比ν仍保持为常数，在此应力处表观泊松比开始增大，到峰值应力时为0.34.粗糙端面条件下，约在70%峰值应力时，泊松比开始增加，峰值应力时的泊松比为0.46.泊松比的上升是由于试样侧向应变较轴向应变增加更快引起的，从图3可以看出，在峰后软化段，随着加载的进行泊松比甚至超过了1.0.

2.2 端面效应对宏观破坏过程的影响

上述强度、变形特征与试样内部微裂纹的萌生、发展和成核过程是密切相关的.图5～8分别为图2中试样在端面光滑与端面粗糙条件下不同加载点(分别为S1，…，S5和R1，…，R5)的损伤演化过程和变形示意图.

图5 光滑端面:试样的损伤演化过程Fig.5 Process of damage for specimen loaded under smooth boundary

图6 光滑端面:试样的变形示意图Fig.6 Deformed configuration for specimen under smooth boundary

图7 粗糙端面:试样的损伤演化过程Fig.7 Process of damage for specimen loaded under rough boundary

图8 粗糙端面:试样的变形示意图Fig.8 Deformed configuration for specimen loaded under rough boundary

对于光滑端面:

(1)最先发生的损伤以及微裂纹相对均匀地分布于试样中.在加载的初始阶段，只有少量相对较弱的、与加载方向大致平行的界面过渡区发生损伤，由于没有端面约束，试样端部的侧向变形未被限制，端部较弱的界面过渡区也发生损伤.

(2)随着加载的进行，与试样高度中央主体部分(相对于端部而言)相似，端部也有越来越多的单元发生损伤，并形成损伤相对集中的局部裂纹，试样最终形成的纵向宏观主裂纹带即是由端部与主体部分的若干局部裂纹扩展、桥接贯通而成.

(3)试样最终的破坏模式为劈裂破坏，贯穿试样的宏观断裂带与加载方向呈小于30°的角度.如图6(c)所示，本文模拟的单轴压缩试样仅产生了一条宏观断裂带，从横向位置来看，宏观断裂带位于试样中部，将试样分割为左右两部分.另外，在试样上端部靠左和下端部靠右有较多单元损伤(见图5(c)～(e))，从破坏特征看，这些部位被压碎了(见图6(c)～(e)).

对于粗糙端面:

(1)最先出现损伤和微裂纹的区域位于试样高度中央主体部分的表层与核心区之间，大致平行加载方向，试样端部极少有单元发生损伤.由于端面约束，试样端部的侧向变形(膨胀)受到限制，且越靠近端面限制越强，故从试样高度中央到端部的侧向拉伸变形越来越小，发生损伤的单元越来越少.

(2)继续加载，试样高度中央主体部分有越来越多的单元发生损伤，而且沿斜向往试样上、下端部，至加载面处转向试样角部，也不断有单元发生损伤.在这些部位，大量的微裂纹彼此相连，形成大片平行于加载方向的两侧表层到核心处的断裂区域，不存在明显的宏观主断裂带.

(3)试样最终的破坏形态为正倒相连的四角锥.破坏最严重的为试样高度中央主体部分，上、下端部因为加载端的约束少有破坏的症状.

图9为van Vliet等[14]对加载板与试件端部之间处于低摩擦和高摩擦约束条件下试件破裂模式的试验研究结果，通过比较可知，上述试样轴压破坏过程的数值结果与典型的物理试验结果是相似的.

图9 不同端面约束条件下试样破坏形态试验结果Fig.9 Experiments results of specimen failure mode loaded under different boundary conditions

在不同的端面约束条件下，虽然试样破坏过程存在上述诸多不同，但是它们的破坏机理是一致的.在数值模型中考虑了材料受拉损伤与剪切损伤2种基本机制，从数值结果可知，无论是光滑端面还是粗糙端面，单轴压缩试样发生剪切损伤的比例均很小，是以拉伸损伤机制控制破坏.图10为残余强度阶段试样的剪切损伤分布，光滑端面条件下发生剪切损伤的单元占总的损伤单元比例约为10%，粗糙端面的约为16%.

图10 不同端面条件下试样的剪切损伤分布Fig.10 Shear damage distributions for specimen loaded under different boundary conditions

综上所述，数值仿真结果复现了混凝土试样的轴压破坏过程.值得一提的是，本文没有采用考虑拉伸软化的损伤本构关系，而是从细观结构特征出发.数值结果表明，混凝土材料的应变软化等宏观非线性力学行为与这些细观结构的渐次损伤密切相关，蕴含了非均匀材料断裂破坏的多尺度损伤物理现象.

3 结 论

(1)从混凝土细观层次的三相结构特征出发，采用复合材料力学中的均质化技巧将界面过渡区和与之相邻的骨料及砂浆基质考虑为均质材料区域，建立了考虑界面过渡区细观特征的复合型界面损伤模型，为进一步揭示混凝土的破坏机理及其非线性行为本质提供了一种新的数值试验手段.

(2)利用该模型对不同端面约束的混凝土的单轴压缩破坏过程进行了数值试验研究，数值模拟得到了与试验结果较为一致的变形特征和破坏过程:试样强度受加载端面约束条件的影响，粗糙端面高于光滑端面，但是弹性模量很接近；不同端面条件下试样应力－应变曲线的峰后软化段延性有明显差异，光滑端面条件下的峰后软化段斜率较陡，具有较低的延性，而粗糙端面的试样软化段下降比较平缓，延性较好；虽然端面约束条件不同试样破坏的宏观表现形式截然不同，光滑端面为轴向劈裂，粗糙端面则是以在试样端部形成倒锥形为特征的破坏形式，但是混凝土材料破坏均由拉伸损伤机制控制.

(3)研究结果表明，端面约束对试验得到的应力－应变曲线形状和损伤局部化过程有很大影响，因此不应笼统地将它们视为单纯的材料特性.同样，可以通过多次的数值试验来单独考虑影响试验结果的一些其他因素，如试样形状、试验机刚度等，为有限的物理试验提供参考甚至在指导工程实践中发挥积极作用.

[1]国家住房和城乡建设部.GB 50010—2010混凝土结构设计规范[S].北京:中国建筑工业出版社，2010.Ministry of Housing and Urban－Rural Development.GB 50010－2010Code for Design of Concrete Structure[S].Beijing:China Architecture＆Building Press，2010.(in Chinese)

[2]van Mier J G M，Shah S P，Arnaud M，etal.Strain－softening of concrete in uniaxial compression[J].Materials and Structures，1997，30(4):195－209.

[3]van Vliet M R A，van Mier J G M.Experimental investigation of concrete under uniaxial compression[J]. Mechanics of Cohesive－frictional Materials，1996，1(1):115－127.

[4]Cusatis G L，Bazant Z P，Cedolin L.Confinementshear lattice model for concrete damage in tension and compression:II.Computation and validation[J].Journal of Engineering Mechanics，2003，129(12):1449－1458.

[5]刘庭金，朱合华，莫海鸿.非均质混凝土破坏过程的细观数值试验[J].岩石力学与工程学报，2005，24(22):4121－4133.LIU Ting－jin， ZHU He－hua， MO Hai－hong.Mesoscopic numerical tests on failure process of heterogeneous concrete[J].Chinese Journal of Rock Mechanics and Engineering，2005，24(22):4121－4133.(in Chinese)

[6]LILLIU G，van Mier J G M.3Dlattice type fracture model for concrete [J]. Engineering Fracture Mechanics，2003，70(7－8):927－941.

[7]Bazant Z P，Tabbara M R，Kazemi M T，etal.Random particle models for fracture of aggregate or fiber composites [J].Journal of Engineering Mechanics，1990，116(8):1686－1705.

[8]刘光廷，王宗敏.用随机骨料模型数值模拟混凝土材料的断裂[J].清华大学学报:自然科学版，1996，36(1):84－89.LIU Guang－ting，WANG Zong－min.Simulation of the fracture of concrete with random aggregate model[J].Journal of Tsinghua University:Science and Technology，1996，36(1):84－89.(in Chinese)

[9]唐春安，朱万成.混凝土损伤与断裂——数值试验[M].北京:科学出版社，2003.TANG Chun－an，ZHU Wan－cheng.Numerical Test of Damage and Fracture of Concrete[M].Beijing:Science Press，2003.(in Chinese)

[10]刘智光，陈健云.混凝土破坏过程的复合型界面损伤模型与数值模拟[J].中南大学学报，2012，43(3):1144－1152.LIU Zhi－guang， CHEN Jian－yun. Composite interface damage model in concrete fracture process and associated numerical simulation [J].Journal of Central South University，2012，43(3):1144－1152.(in Chinese)

[11]刘智光，陈健云.考虑材料组成特性的混凝土轴拉破坏过程细观数值模拟[J].工程力学，2012，29(7):136－146.LIU Zhi－guang，CHEN Jian－yun.Meso－structural analysis of concrete specimens under uniaxial tension based on composition characteristics [J].Engineering Mechanics，2012，29(7):136－146.(in Chinese)

[12]Walraven J C， Reinhardt H W. Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjected to shear loading[J].HERON，1981，26(1A):26－35.

[13]陈惠发，萨里普A F.混凝土和土的本构方程[M].余天庆，王勋文，刘西拉，等，译.北京:中国建筑工业出版社，2004.CHEN Hui－fa，Saleeb A F.Constitutive Equations for Materials of Concrete and Soil[M].YU Tianqing，WANG Xun－wen，LIU Xi－la，etal，tran.Beijing:China Architecture ＆ Building Press，2004.(in Chinese)

[14]van Vliet M R A，van Mier J G M.Softening behaviour of concrete under uniaxial compression[C]／／ Wittmann F H，ed.Fracture Mechanics of Concrete Structures. Freiburg: Aedificatio Publishers，1995:383－396.