基于中轴变换的刀具优化选择与刀具路径规划

巴 文 兰， 曹 利 新

(大连理工大学 机械工程学院，辽宁 大连 116024)

0 引 言

近10年间，计算机集成设计、制造技术有了快速的发展，在许多CAD／CAM软件中可以完成复杂几何体的构造、刀位规划、干涉检验、G代码生成.然而，现有的CAD／CAM软件仍然存在着一些不足，如目前的CAD／CAM系统只支持针对单一尺寸的刀具生成给定区域的加工刀具路径，并要求用户选择刀具尺寸.迫于无奈，编程人员不得不做出一些主观的、保守的选择，这将导致加工时间变长、加工成本提高，特别是给定区域内包含瓶颈区域或边界曲线具有较小的曲率半径时.随着加工中心中快速换刀装置的出现，采用多种尺寸刀具加工模具型腔等工件成为可能.

对于模具型腔的2轴半加工，通常采用平头刀对模具毛坯进行分层粗加工，之后再利用球头刀对其进行精加工.粗加工要去除毛坯上大部分加工余量，为了提高加工效率，粗加工应尽可能采用较大直径的刀具，这样可以有效地缩短刀具切削路径的长度，同时直径大的刀具刚度高，切削过程的稳定性好，可见刀具尺寸的优化选择和刀具路径的合理规划对于提高加工效率、降低加工成本至关重要.目前，针对刀具尺寸选择的研究相对较少，Marshall等[1]提出了基于几何干涉检验的单一刀具尺寸的选择方法，即找出给定加工区域中无干涉的最大内接圆，刀具直径不能超过该圆的直径.Bala等[2]提出了2轴半模具加工的两把刀具尺寸确定方法，较小的刀具按模具轮廓的最小曲率半径选取，而较大的刀具则应使该刀具加工后剩余的未加工区域可被直径较小的刀具清根加工完成.1997年，Gau[3]针对模具型腔的2轴半粗加工，提出了Voronoi山的概念，并给出了确定刀具尺寸优化集的动态规划方法，该方法直观地描述了给定刀具的可行域即为给定刀具半径决定的截平面与被加工区域边界轮廓的Voronoi山的交线，这一方法虽然非常直观，但涉及形成Voronoi山的直纹面与平面的求交过程，计算量较大.

给定区域的中轴变换结果包含着丰富的几何学信息，对于给定平面内的封闭区域，可以用其边界曲线来描述，也可以通过中轴变换得到的中轴线和中轴变换圆来描述.前者从封闭区域的外部描述给定区域，后者则从封闭区域的内部描述该区域.Cao等前期曾对平面域中轴变换的理论与算法进行过深入研究[4－6]，主要内容包括:应用微分几何学中活动标架和相伴曲线方法，建立了边界曲线与中轴线的法向映射关系、尺度变换及曲率之间的内在联系，构造了一种新的计算中轴线的轨迹跟踪算法，克服了目前中轴线的近似算法和迭代算法所带来的缺陷；在跟踪算法的基础上，提出了中轴变换的两切点圆精确算法和计算分叉点的三切点圆精确算法；研究了中轴变换圆沿中轴线运动的包络曲线计算过程，即中轴变换的反问题；进一步研究发现平面封闭域内中轴线上的点满足到边界曲线的最小距离最大化的特性，即鞍点特性，它揭示了中轴变换的本质属性，进而建立了平面域中轴变换鞍点规划模型，提出了相应的解算方法，形成与前面算法相平行的另一种中轴线计算方法.充分挖掘中轴变换结果中所蕴涵的信息可以解决工程中的一系列关键问题，如Smith等[7]针对数控加工的截平面方法，提出了一种利用中轴变换优化选择平行平面方向的算法.Elber等[8]利用中轴变换理论，提出了适合模具型腔高速数控加工的刀具路径规划方法.本文试图利用中轴变换思想来解决模具型腔加工中的刀具尺寸优化选择问题.

1 基于中轴变换的刀具尺寸优化选择方法

利用中轴变换算法[4－6]，可以得到平面封闭区域中轴线上的一系列离散点，包括端点、正常点和分叉点.设给定平面Π0内的封闭区域Ω，其中轴线为M(X(t)，Y(t))，相应的半径函数为r(t)，t为中轴线的曲线参数.若将半径函数r(t)看作中轴线M的Z坐标，则可用三维空间曲线M＊来表示中轴变换，如图1所示.这些三维空间曲线在平面上的投影则对应中轴线M，三维空间曲线M＊的Z坐标分量决定了平面Π0上对应区域的尺度大小，Z值愈大，表示该区域的中轴变换圆半径愈大，加工时可以采用直径较大的刀具而不会发生干涉；相反，Z值愈小，对应平面区域的中轴变换圆半径也愈小，只能采用直径较小的刀具加工该区域.传统的数控加工一般按照不发生干涉的最小曲率半径选择刀具尺寸，进而生成相应的刀具路径，因此切削路径较长、效率低、成本高.本文在中轴变换的基础上，根据被加工区域的大小选择合适的平头铣刀刀具尺寸，进而获得优化的数控加工刀具路径.具体地说，将一个平面封闭区域的加工分为粗加工、清角加工和清根加工3个步骤.粗加工阶段选择直径较大的刀具，完成平面封闭区域内大部分余量的切削；清角加工主要针对粗加工残留下的不能加工区域，逐次减小刀具直径，完成封闭区域内细长区域的加工；清根加工按照封闭轮廓曲线的最小曲率半径选择刀具尺寸，完成边界的加工.

为了实现下文所提的基于刀具尺寸优化选择的刀具路径规划，或者为了计算给定尺寸刀具的可加工范围，均需要对三维中轴线与给定高度平面的交点进行计算，因此，应将中轴线上的离散点用曲线方程来表示，本文采用常用的三次B样条插值方法.考虑到给定区域的中轴线在分叉点处，中轴线的一阶导数、二阶导数等均不连续，因此分叉点两侧的中轴线必须分段表示.根据中轴线上端点和分叉点的个数，确定用几段B样条插值曲线来表示中轴线.如图1所示，需要5段B样条插值曲线来表示该矩形的三维中轴线.

图1 平面给定区域的中轴线与半径函数Fig.1 Medial axis and radial function for a closed planar domain

2 粗加工

对于给定区域的数控加工刀具尺寸选择来说，通过中轴变换可以更加深入地认识封闭区域本身，如给定封闭区域的最大中轴变换圆直径决定了数控加工中不发生干涉的最大刀具直径.若刀具直径Dc超过该最大中轴变换圆的直径Dmax，则会引起干涉，因此Dc≤Dmax；相反，若粗加工刀具直径太小，则切削行距减小，刀具切削路径变长，影响加工效率.同时由于刀具直径小、刚度低，切削力引起的变形将增大，若通过减小切削用量来控制变形，将会进一步降低加工效率.

从数控加工刀具路径规划的角度来看，经常需要知道某加工区域在给定刀具直径下，不发生干涉的刀具切削路径和刀具沿该切削路径运动的覆盖范围，即加工区域.这一问题相当于用平行于底面且高度等于平头铣刀刀具半径的平面Π截取图1中的三维空间曲线，平面Π之上的三维空间曲线则描述了给定尺寸刀具的可加工范围，即平面Π之上的三维空间曲线所对应的中轴变换圆沿其中轴线运动所覆盖的区域，该加工范围的边界曲线为C，如图2所示.若粗加工刀具直径Dc满足不等式1≤Dmax／Dc≤2，则只需一个环切行程即可完成相应的粗加工工作，如图3(a)所示，Dmax＝50mm，Dc＝30mm，图中给出了半径函数大于等于刀具半径的中轴线以及中轴变换圆的包络.图3(b)表示刀具沿包络线的等距线(图中虚线)运动，一次切削行程即可覆盖整个粗加工区域(图3(b)中阴影部分)，等距距离为刀具半径.若刀具直径Dc满足不等式Dmax／Dc＞2，则给定的封闭区域需多次切削行程才能完成，如图3(c)所示，Dmax＝50mm，Dc＝10mm，若取加工行距为刀具直径，则粗加工需3次切削行程，刀具路径为边界曲线C按刀具半径生成的等距线.

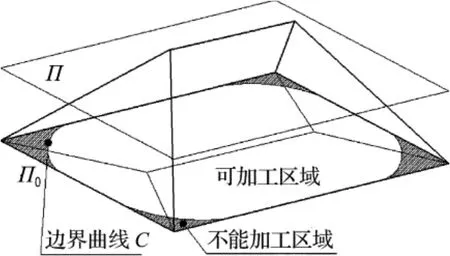
图2 刀具尺寸与中轴线的关系Fig.2 Relations between cutter′s size and medial axis

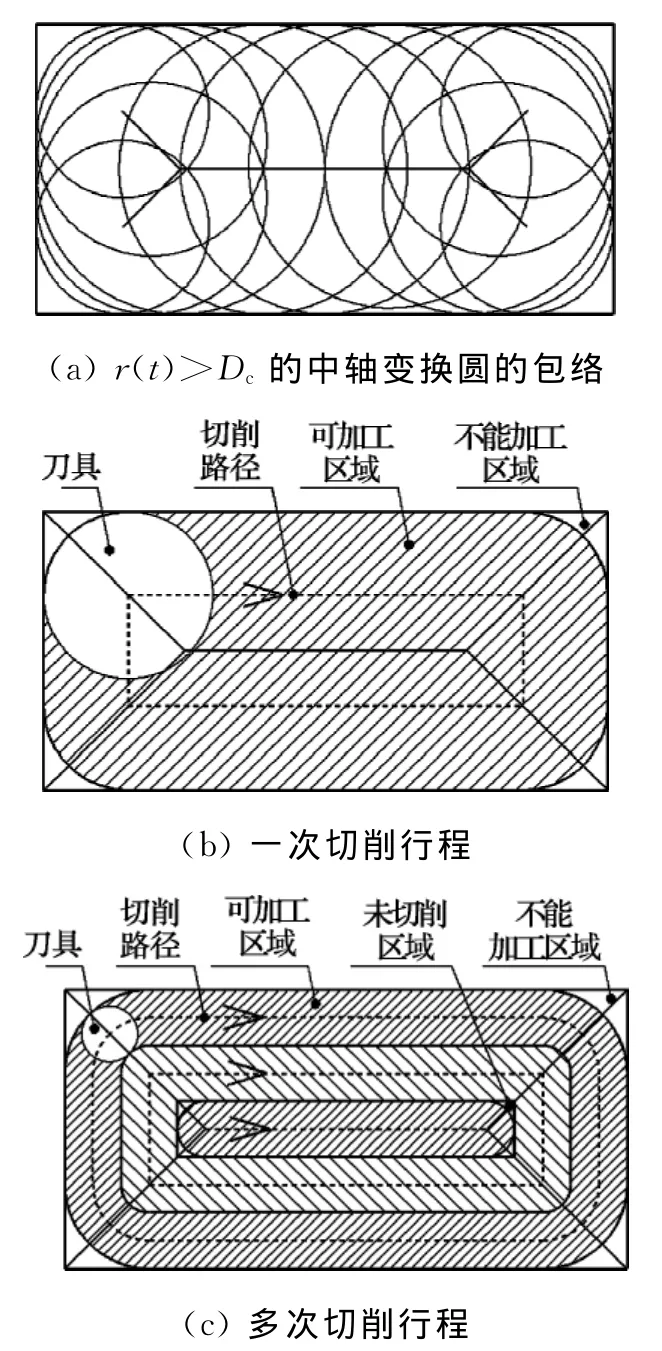
图3 给定尺寸刀具的可加工范围Fig.3 Accessible area of given sized cutter

对图3(c)进行局部放大，如图4所示，可以发现行距为刀具直径时，在切削路径的转角处存在未切削区域.影响未切削区域大小的因素有刀具半径R、加工行距H和转角α，如图5所示.为了不存在未切削区域，这三者间的关系应满足:由上式可见，α愈小，未切削区域愈大，因此相应的加工行距愈小.该未切削区域除了可以通过减小行距的方法消除外，也可通过补刀加工来完成，即先按照给定行距进行环切加工，之后对残留的未切削区域进行补刀.由于未切削区域一定发生在中轴线上，如图3(c)所示，刀具沿着中轴线运动即可完成补刀切削.应当指出，未切削区域不同于前面提到的不能加工区域，不能加工区域不能通过减小加工行距或改变切削路径完成，只能采用直径较小的刀具在后续的加工中完成.

图4 影响未切削区域大小的因素Fig.4 Uncut areas and related factors

图5 无未切削区域的最大加工行距Fig.5 Maximum pass interval for non－uncut area

总之，为了提高粗加工的加工效率，在不发生干涉的前提下，刀具直径尽可能取较大值.若粗加工刀具直径的选择范围为Dmax／2≤Dc≤Dmax，Dc通常取该范围内的标准值，则一次切削行程即可覆盖封闭区域的主要部分(最大中轴变换圆附近区域)；若Dc＜Dmax／2，则粗加工需要多次切削行程，同时要考虑未切削区域的处理；若Dc＞Dmax，则会引起加工干涉.

3 单向清角加工与清根加工

粗加工后，在封闭区域的转角或中间瓶颈处残留材料，需要进一步切削，该区域称为前次刀具不能加工区域，即封闭区域中前次刀具不可达区域，如图3所示的4个转角处，需要通过清角加工来完成.清角前需要计算前次使用刀具所残留的不能加工区域的大小，即给定加工区域去掉前面刀具的已加工区域.对于每个转角区域，若采用一般的环切法清角，需计算该区域的最大中轴变换圆，如图6(a)，并选择不发生干涉的刀具直径，按环切法规划刀具路径，这种方法如同上文的粗加工策略，为了不产生干涉并一刀完成该区域的切削，需要重新进行中轴变换，而且环切后又会留下更多的不能加工区域需要清角，如图6(b).显然，这种方法过于复杂.

图6 环切法清角Fig.6 Cleaning the corner by loop method

本文提出一种单向清角策略，如图7所示，对于给定清角区域，刀具从一侧进去，从另一侧出来，刀具路径顺着清角轮廓的边界进行.为了选择合适的刀具尺寸，需要计算中轴线与边界曲线的交点P，如图7(a)所示，设该点所对应的中轴变换圆的直径为Dmax1，以此作为确定清角加工刀具尺寸的依据.为了能够一次切削完成清角余量，本文取清角刀具的直径Dc1满足不等式Dmax1／2≤Dc1＜Dc，Dc为粗加工的刀具直径或前次清角加工的刀具直径，从图7(b)可以看出，Dc1愈小，一次切削可加工的区域就愈大，图7(b)中取Dc1＝Dmax1／2，阴影部分为本次清角可切削部分.对于粗加工后存在多个角需要清理的情况，为了避免频繁换刀，且刀具直径变化不大的情况，可以计算中轴线与各个转角处边界曲线的交点P1，…，Pn，取各点所对应的中轴变换圆直径的最大值max(Dmax1，Dmax2，…，Dmaxn)作为本次清角的刀具直径.重复上述操作，即可完成全部转角和细长区域的清角加工.

图7 单向清角Fig.7 Cleaning the corner by one way method

清角加工后需要对轮廓边界进行清根加工，以封闭边界曲线的最小凸曲率半径的圆整值作为清根刀具半径，以边界曲线的等距线作为刀具路径，即可实现最终的清根加工.

上述粗加工、清角加工和清根加工给出了刀具尺寸选择所需满足的不等式，考虑到实际生产中刀具尺寸已标准化，需将满足上述不等式的刀具尺寸圆整为标准刀具尺寸值，便于在刀具集中选择最佳刀具.

4 刀位点的计算与连接／切削路径长度

如前所述，加工区域为两平面所夹空间曲线对应中轴变换圆的覆盖范围，其边界曲线为中轴变换圆沿中轴线运动的包络线，设给定平面域的中轴变换为r(t)＝ (x(t)y(t)r(t))，由文献[4]，则可得中轴变换的包络线方程:

式中:i、j为平面内固定直角坐标系的单位矢量；x′、y′、r′分别为中轴线的坐标x、y和半径函数r对参数t的一阶导数.“±”和“”表示中轴线上参数为t的一个点，对应包络线上两个特征点.中轴变换圆的包络线形成了边界曲线；刀具运动轨迹即为边界曲线的等距线，等距距离为刀具半径，其方程可表示为

式中:R为刀具半径.r－R≥0，则等距线不会出现自交现象.为了形成连续的刀具切削路径，需对这些特征点按照相邻点距离最短原则进行排序，最终形成刀具切削路径.

5 数值算例

算例1 给定边界曲线为具有两个孔洞的鹅掌楸树叶的边界.该封闭区域的中轴线和中轴变换圆如图8所示，最大中轴变换圆直径为46.856 mm，边界曲线的最小凸曲率半径为0.658mm.以中轴线的端点或分叉点作为曲线端点，将中轴线和半径函数表示为三维B样条曲线段，结果如图9所示.利用前面提出的加工策略，确定该封闭区域粗加工的刀具直径为24mm，清角加工的刀具直径分别为10、5、2mm，清根加工的刀具直径为1.3mm.图10(a)为粗加工阶段的刀具覆盖范围；图10(b)～(d)中的红色、绿色和黄色部分分别为3次清角加工所对应的刀具覆盖范围；图10(e)中的紫色为清根加工对应的刀具覆盖范围；图10(f)为3个加工阶段所对应的刀具路径.

图8 算例1中轴线与中轴变换圆Fig.8 Medial axis and medial axis circles for Example 1

图9 算例1中轴线与半径函数的三维表示Fig.9 3Drepresentation of medial axis and radial function for Example 1

图10 算例1多刀加工顺序与刀具路径Fig.10 Machining sequence of multicutters and cutting tool－path for Example 1

算例2 给定边界曲线为枫树叶的边界.该封闭区域的中轴线和中轴变换圆如图11所示，最大中轴变换圆直径为80.434mm，边界曲线的最小凸曲率半径为0.523mm.以中轴线的端点或分叉点作为曲线端点，将中轴线和半径函数表示为三维B样条曲线段，结果如图12所示.利用前面提出的加工策略，确定该封闭区域粗加工的刀具直径为41mm，清角加工的刀具直径分别为17、6、2mm，清根加工的刀具直径为1mm.图13(a)为粗加工阶段的刀具覆盖范围；图13(b)～(d)中的红色、绿色和黄色部分分别为3次清角加工所对应的刀具覆盖范围；图13(e)中的紫色为清根加工对应的刀具覆盖范围；图13(f)为3个加工阶段所对应的刀具路径.

图11 算例2中轴线与中轴变换圆Fig.11 Medial axis and medial axis circles for Example 2

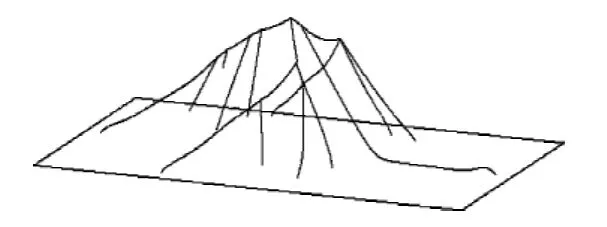
图12 算例2中轴线与半径函数的三维表示Fig.12 3Drepresentation of medial axis and radial function for Example 2

图13 算例2多刀加工顺序与刀具路径Fig.13 Machining sequence by multicutters and cutting tool－path for Example 2

6 结 论

(1)在对给定加工区域进行中轴变换的基础上，将由分叉点分开的中轴线和半径函数进行分段B样条曲线插值，通过计算给定刀具半径确定的截平面与中轴变换得到的三维空间曲线族的交点，确定相应尺寸刀具的加工可行域并规划刀具运动轨迹.该方法不需要构造被加工区域边界轮廓的Voronoi山，同时避免了计算多尺寸刀具确定的截平面与被加工区域边界轮廓的Voronoi山的求交过程，以线面求交代替传统的面面求交，方法简单、效率高.

(2)以最大中轴变换圆为依据，确定粗加工的刀具直径.若最大中轴变换圆的直径与刀具直径的比值介于1～2，则只需一次切削行程即可完成相应的粗加工工作；若该比值大于2，则给定的区域需多次切削才能完成，多次切削加工中可能存在的未切削区域可通过刀具沿中轴线补刀来完成；若该比值小于1，则必发生加工干涉.

(3)根据粗加工后残留未加工区域对应的中轴变换结果，提出一种单向清角方法.该方法通过计算中轴线与已加工区域所对应的边界曲线的交点，将该点所对应的中轴变换圆的直径作为确定清角加工刀具尺寸的依据；清根加工的刀具半径则取封闭边界曲线的最小凸曲率半径的圆整值.

(4)对于给定区域内包含瓶颈区域或边界曲线具有较小的曲率半径的加工区域，利用本文所提方法可以优化选择数控加工各阶段的刀具尺寸，所生成的刀具切削路径长度将大幅度地缩短，从而提高加工效率.

[1]Marshall S，Griftiths G J.A survey of cutter－path construction techniques for milling machines [J].International Journal of Production Research，1994，32(12):2861－2877.

[2]Bala M，Chang T C.Automatic cutter selection and cutter path generation for prismatic parts [J].International Journal of Production Research，1991，29(11):2163－2176.

[3]Gau Y S.Optimal tool set selection and tool path planning for 3－axis CNC milling [D].Madison:University of Wisconsin－Madison，1997.

[4]CAO Li－xin，LIU Jun.Computation of medial axis and offset curves of curved boundaries in planar domain[J].Computer－Aided Design，2008，40(4):465－475.

[5]CAO Li－xin，JIA Zhen－yuan，LIU Jun.Computation of medial axis and offset curves of curved boundaries in planar domains based on the Cesaro′s approach[J].Computer Aided Geometric Design，2009，26(4):444－454.

[6]CAO Li－xin，BA Wen－lan，LIU Jun.Computation of the medial axis of planar domains based on saddle point programming [J].Computer－Aided Design，2011，43(8):979－988.

[7]Smith T S，Farouki R T，Al－Kandari M，etal.Optimal slicing of free－form surfaces[J].Computer Aided Geometric Design，2002，19(1):43－64.

[8]Elber G，Cohen E，Drake S.MATHSM:medial axis transform toward high speed machining of pockets[J].Computer－Aided Design，2005，37(2):241－250.