羊绒鳞片图纹基因码的构成及其相互关系

石先军，蔡光明，于伟东

(1.武汉纺织大学 数学与计算机学院，湖北 武汉 430073;2.武汉纺织大学 纺织学院，湖北 武汉 430073)

山羊绒属珍稀动物纤维，具有轻、柔、细、滑的品质特征，一直是纺织工业界公认的最具经济价值，品质最优秀的毛发类纤维。由其制成的纺织品更是手感柔软、滑糯，风格舒雅、高贵，深受人们的推宠。由于山羊绒产量很低，在中国平均年产量仅为18 000 t左右，且已占到世界总产量的70%［1］，故其价格非常昂贵，所以工业上通常将其与其他毛发类纤维尤其是羊毛进行混纺，以改善纱线品质并降低成本。由于原料价格的差异，不同羊绒含量的纺织品价格也存在巨大的差异。显然，明确混纺产品的混纺比例，既是保护消费者权益的需要，也是保证产品真实物质品质的需要。

对于混纺比例的确定，最重要的任务就是对羊绒与相似纤维进行准确鉴别，而后通过相应的计算公式［2-4］计算出混合比例。本文的研究团队一直从理论上探讨光学显微镜下羊绒与相似纤维尤其是细羊毛纤维的鉴别原理以及理论上羊绒最高识别精度。本文主要讨论光学显微镜下羊绒鳞片图纹特征的表达以及描述其各形状参数的相互关系。

1 动物纤维鳞片的图纹特征

所有的毛发类纤维都有一个共同的特征，即纤维的表面覆盖着一层形状各异的鳞片。常见的动物毛发纤维，其表面鳞片图纹特征大致可分为5种类型［5-6］：马赛克状、V形状、平行线状、栉齿状以及花瓣状(见表1)。

鳞片图纹是描述纤维表面外观形态特征的基本形式，是纤维形态的根本表达。它包括了纤维表面鳞片的各种几何特征，如鳞片的高、宽、面积、周长、边缘波纹、完整性、厚度、伪鳞脊等。这些特征是展示纤维差别的最主要特征，它们类似于人的指纹或脸谱。不同动物种群的毛发，其表面鳞片的形态特征不同［7-8］;即便是同一动物种群，不同的品系间其纤维鳞片也具有不同的图纹特征。

表1 常见的动物毛发类纤维的鳞片图纹特征Tab.1 Scale patterns of common animal fibers

正是由于动物纤维鳞片图纹特征的差异性，自1954 年 Wildamn［5］出版了著作“The Microscopy of Animal Textile Fibers”以后，学者们对于动物纤维的鉴别都依循着他的研究方向来进行，即依据纤维表面的鳞片图纹特征来辨识纤维。羊绒与其他相似毛发类纤维的鉴别也不例外，普遍采用的判别依据就是羊绒的鳞片图纹特征。

2 羊绒鳞片的图纹特征

文献［9-11］详细地描述了羊绒鳞片的图纹特征。从表面形态来看，羊绒的鳞片多呈环状包覆毛干，鳞片较薄，表面光滑，边缘清晰，单位长度上鳞片个数较少;而羊毛的鳞片大多数呈环状少，数呈瓦片状包覆毛干，其鳞片较厚，表面粗糙不光滑，边缘线较粗不太清晰，单位长度上鳞片个数较多。具体情况见表2。

显然，表2示出了扫描电镜和光学显微镜观察出的关于羊绒鳞片图纹特征的定性描述。事实上，由于光学显微镜下鳞片的厚度是模糊不清的，此时这一指标并不能用来描述羊绒鳞片图纹特征。通过观察发现，光学显微镜下清晰可见的描述羊绒鳞片图纹特征的指标大致可以分为9大类，共18个指标。这18个指标为：鳞片面积 A及其变异系数ACV、鳞片周长P及其变异系数 PCV、鳞片(纤维)直径d及其变异系数 dCV、鳞片高度 h及其变异系数hCV、鳞片最大高度 hmax及其变异系数、鳞片相对面积RA(RA=A/d2)及其变异系数、鳞片相对周长RP(RP=P/d)及其变异系数、鳞片相对高度即径高比Rh(Rh=d/h)及其变异系数和鳞片矩形度Rt(Rt=A/(P/4)2)及其变异系数 。

在这18个指标中，有些指标直接描述了纤维鳞片的图纹特征，如鳞片高度直接描述了纤维鳞片纵向上的1个图纹特征，而有些指标则综合或间接地描述了鳞片的图纹特征，如鳞片的环状包覆完整性，可用 A、P、RA、RP以及 Rt指标综合表达。鳞片边缘的波动和方向，可用指标RA和Rt间接表达。

表2 山羊绒与细羊毛纤维鳞片的图纹特征Tab.2 Scale patterns of cashmere and fine wool

虽然还有其他指标可以用来描述羊绒鳞片的图纹特征，但总的来看，上述18个指标比较全面地描述了光学显微镜下纤维鳞片的图纹特征。

3 羊绒鳞片图纹基因码的构成

因为羊绒的鳞片图纹具有指纹性，故将有关羊绒鳞片图纹的各参数指标及其组合统称为鳞片图纹基因码。

理论上完全相互独立的鳞片图纹最基本的几何参数被称为基基因。如鳞片的高、宽、面积、周长、边缘波纹、完整性、厚度、伪鳞脊等特征参数。由基基因相对某一基本不变的基基因做商或互为放大缩小其特征的基基因的乘积或商而得的基因码，称为复基因。如鳞片相对周长就是鳞片的实测周长与其直径之商。用于判别鳞片图纹码归属何类毛发纤维的基因码组合，称为基因组合。1组具有最佳判率的基因码组合称为最优基因组。

羊绒鳞片的图纹基因码即由上述3类基因码或组合构成。从理论上来说，只要把这3类关于羊绒辨识的基因码或组合情况搞清楚，就可明确羊绒的理论识别精度。

4 鳞片图纹基因码之间的相互关系

事实上，在羊绒与相似纤维的检测辨识中，单个基基因或复基因在羊绒的辨识精度上都是有限的，实用中更多的是使用1个或几个基因组合去进行羊绒纤维的检测识别。一般而言，在1个基因组合中通常会包含几个基基因或复基因，这些基基因或复基因在羊绒纤维的识别机制方面是不完全相同的。从理论上来说，如果某基因组合中所有的基基因或复基因在羊绒纤维的识别机制上是完全不同的，即各基因码之间相互独立，则此基因组合能最大限度地发挥每个基因码对羊绒的识别能力，这种基因组合对羊绒纤维具有较高的识别精度。

将上述所提到的所有基因码进行独立性检验，在显著性水平为0.05，检验方式为双尾T-检验下的结果见表3～5。表中第 1行数据为相关系数，第2行数据为检验P值。

表3 基基因的相关性分析Tab.3 Correlation analysis for primary genes

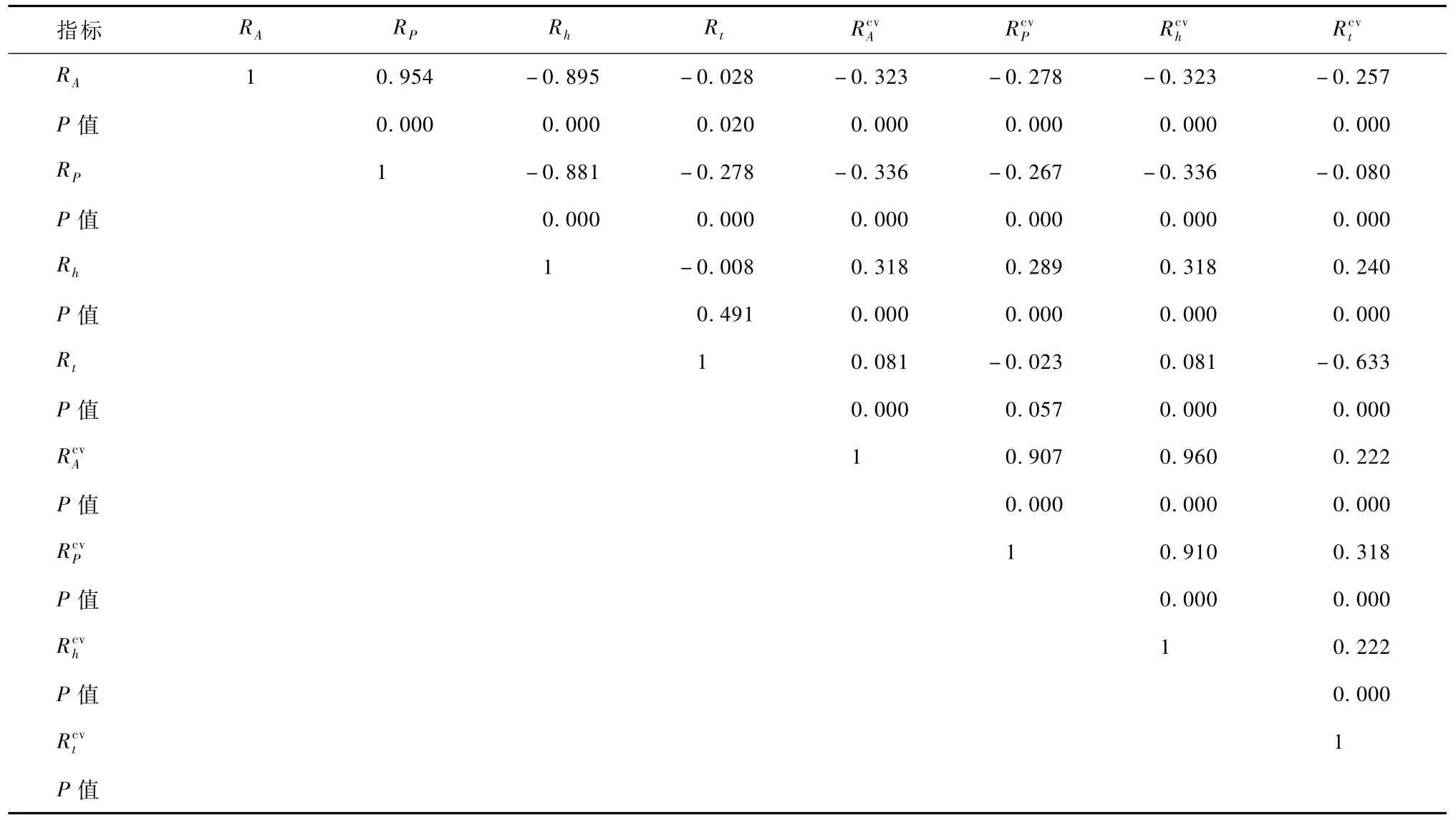
表4 复基因的相关性分析Tab.4 Correlation analysis for recombinant gene

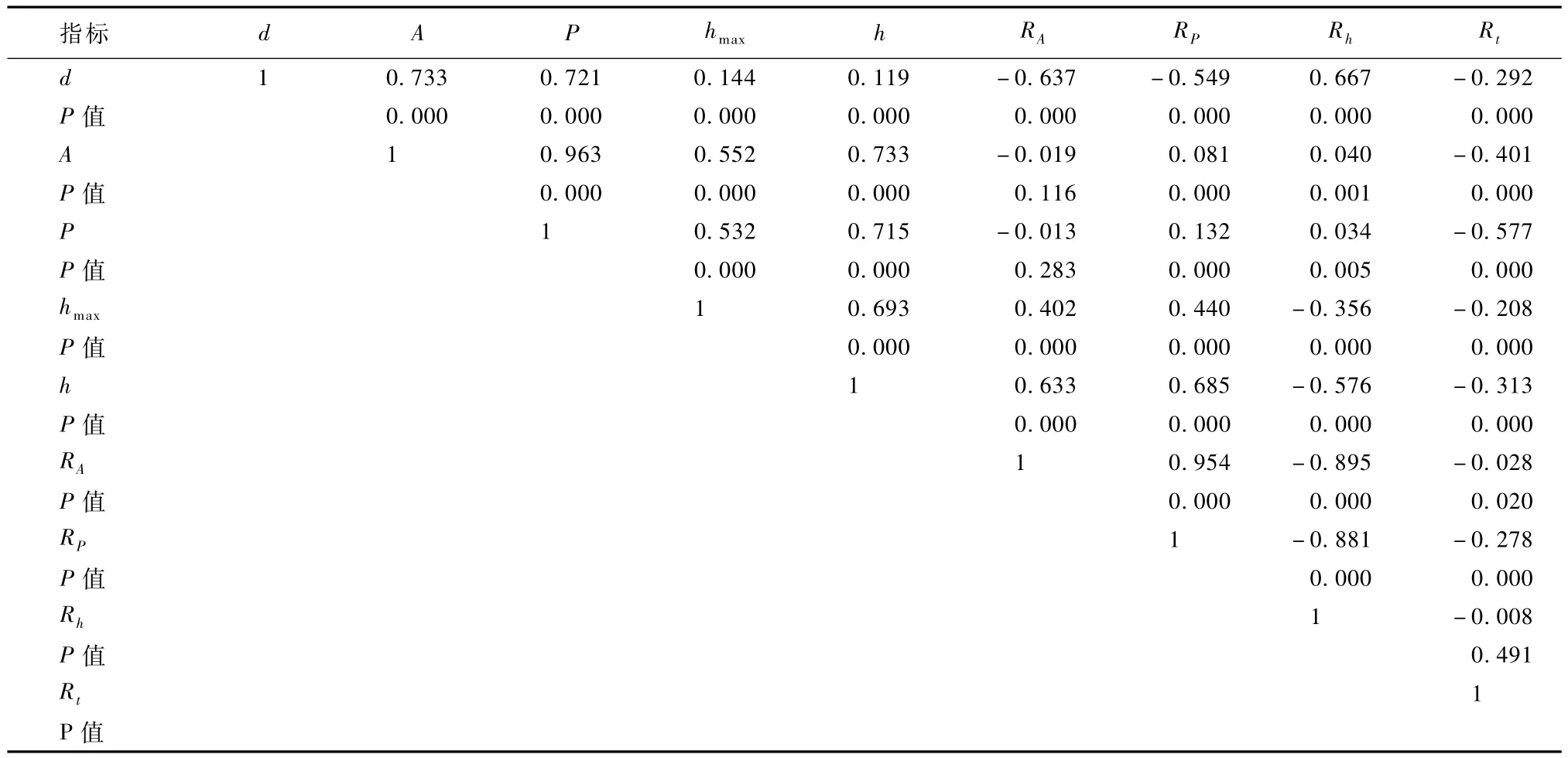
表5 基基因与复基因的相关性分析Tab.5 Correlation analysis between primary gene and recombinant gene

从表3可看出，在所有的基基因中，基基因d与所有其他的基基因均相关，其中与基基因A和P具有较强的正相关性，而与其他7个基基因具有较弱的正相关性。其原因很容易理解，因为不论是羊绒还是羊毛纤维，直径越粗，其周长或面积必然增加。基基因A与基基因P具有很强的正相关性，也与基基因h具有较强的正相关性，与其他5个基基因具有很弱的负相关性。基基因P与h具有较强的正相关性，同时基基因 hmax与h、基基因ACV与PCV和hCV、基基因PCV与hCV以及 hcvmax和hCV都具有很强的正相关性。值得一提是基基因dCV与基基因ACV、PCV、hcvmax、hCV是不相关的。这表明，纤维直径的均匀性与鳞片面积、周长、高度及最大高度是否一致无关。除此以外，其他的基基因相互之间为正相关或为负相关。

从表4可看出，在0.05的显著性水平下，所有的复基因中只有 Rh和 Rt以及 Rt和是不相关的，其他的复基因两两之间均具有相关性，或为正相关或为负相关。其中，复基因 RA和 RP、和和以及和均具有很强的正相关性，RA和Rh以及RP和Rh均有较强的负相关性。

从表5可看出，在0.05的显著性水平下，除了基因 A和 RA、P和 RA以及 Rh和 Rt不相关以外，其他所有的基因均是相关的。

以上所有的数据均表明：鳞片图纹基因码之间基本上都具有相关性，只有少数几个基因码之间不存在相关性。这说明不同的基因码之间关于羊绒的识别机制具有一定的重叠性。于是问题变得明朗，只要明确单个鳞片图纹基因码对羊绒的辨识精度，那么依据这些辨别精度并结合基因码间的相互关系对基因码进行组合，即可得到具有较高判率的最优基因组。

5 结论

本文研究了光学显微镜下基于鳞片图纹基因码的羊绒识别原理。在光学显微镜下发现，羊绒鳞片的图纹特征可以用18个参数指标来全面描述，这些指标分别描述了鳞片纵向、横向以及局部区域上的形状特征及其细节。基于这些图纹参数，提出了图纹基因码的概念并讨论了其构成，这使得可以借用数学的理论和知识来系统地讨论羊绒的识别问题。
通过对鳞片图纹基因码的相关性讨论发现，光学显微镜下的鳞片图纹基因码大多存在相关性，只有少数图纹基因码间不存在相关性。其原因很容易理解，因为鳞片的每个图纹基因码描述的是鳞片某一方面的形状特征，而鳞片的不同形状特征或多或少总存在一定的关系，故鳞片图纹基因码的相关性研究为发现羊绒识别准则指明了方向：首先明确单个基因码对羊绒的辨识精度，然后依据这些辨别精度并结合基因码间的相互关系构造最优基因组，即可实现高准确度的羊绒判别。

［1］中国国家统计局.中国统计年鉴 2011［M］.北京：中国统计出版社，2011：1-1057.National Bureau of Statistics of China.China Statistical Yearbook 2011［M］.Beijing：China Statistics Press，2011：1-1057.

［2］WORTMANN F J，ARMS W.Quantitative fibre mixture analysis by scanning electron microscopy，part I：blends of mahair and cashmere with sheep's wool［J］.Textile Res J，1986，56(7)：442-446.

［3］WORTMANN F J.Quantitative fibre mixture analysis by scanning electron microscopy，partⅢ：round trial results on mohair/wool blends［J］.Textile Res J，1991，61：371-374.

［4］WORTMANNFJ， PHANKH， AUGUSTINP.Quantitative fiber mixture analysis by scanning electron microscopy，part V：analyzing pure fiber samples and samples with small admixtures according to test method IWTO58［J］.Textile Res J，2003，73(8)：727-732.

［5］WILDMAN A B，The Microscopy of Animal Textile Fibres［M］.Leeds：Wool Industry Research Assoc，1954：209.

［6］HASANZADEH P R，FAEZ K，ASLANZADEH S.Feature extraction of scale pattern in animal textile fibers［C］//WSCG POSTER Proceedings of the 12th International Conference in Central Europe on Computer Graphics，Visualization and Computer Vision'2004.Plzen：UNION Agency-Science Press，2004：53-56.

［7］SATO H，MATSUDA H，KUBOTA S，et al.Statistical comparison of dog and cat guard hairs using numerical morphology［J］.Forensic Science International，2006，158：94-103.

［8］SAHAJPAL V，GOYAL S P，JAYAPAL R，et al.Hair characteristics of four Indian bear species［J］.Science and Justice，2008，48：8-15.

［9］石先军，于伟东，袁子厚.基于贝叶斯方法的山羊绒与细羊毛的鉴别［J］.纺织学报，2008，29(1)：26-28，33.SHI Xianjun， YU Weidong， YUAN Zihou.An identification method for cashmere and fine wool based on Bayes model［J］.Journal of Textile Research，2008，29(1)：26-28，33.

［10］SHI Xianjun，YU Weidong.Classification of animal fibers based on microscopic image［J］.Journal of Applied Sciences，2009，27(1)：62-66.

［11］侯秀良.山羊绒纤维结构与热学性能研究［D］.上海：东华大学，2002：4-8.HOU Xiuliang.The structures and thermal properties of cashmere fiber［D］.Shanghai：Donghua University，2002：4-8.