排架式微型桩组合结构受力分析

徐小林，王全才，王 浩，吴 清

（1.中国科学院 山地灾害与地表过程重点实验室，四川 成都610041；2.中国科学院 水利部 成都山地灾害与环境研究所，四川 成都610041；3.中国科学院大学，北京100049）

微型桩最初由意大利人Fernando Lizzi于20世纪50年代提出来，之后Armour等［1］对微型桩的应用做了相对全面的阐述。微型桩成孔直径一般在10～30 cm，通常以组合形式的群桩出现，起初主要用来承受竖向荷载，对于承受水平荷载的微型桩理论，近年来国内外学者也做了一些相关研究［2－5］。冯君等［6］将微型桩体系和桩间岩土体视为桩—岩土体复合结构，建立分析模型，并加以计算；肖世国等［7］按弹性地基梁理论对微型桩滑面上下部分分别用“m”法和“k”法进行了计算分析（k法：弹性抗力系数k为定值；m法：弹性抗力系数m随深度线性变化）；周德培等［8］总结了微型桩组合结构布置形式，并按照桩土作用原理，在弹性地基梁理论基础上提出了一种组合结构的计算公式。国内部分学者对于地震力下微型桩变形及内力也做了相关研究［9－11］。罗红名等［12］针对规范中拟静力法的地震力作用方向为水平方向，提出考虑地震力最危险方向的计算方法。不过与微型桩越来越广泛的应用相比，其计算理论的研究却仍然显得比较滞后。

本文在前人研究的基础上，针对微型桩处治对象多为小型滑坡或不稳定边坡（以下通称为滑坡）的特点，认识到不稳定坡体完全不同于一般可以提供正常地基反力的地基的实际情况，从分析微型桩排架组合结构本身、结构与土体对外力的响应和反力作用条件入手，注意到组合结构中不同位置的微型桩前抗力和微型桩不同高度地基反力的明显差别，在弹性地基梁理论的基础上，借鉴一般微型桩水平承载力计算的思路，通过不同的m计算值（考虑到组合结构中桩的位置不同，效果不同，导致相应的荷载及位移不同，计算出的m的值就不一样；同时，考虑到要保证桩间土体不被挤出，从而对m值产生影响）和桩顶大变形对m值的限定条件，来体现微型桩前其他微型桩的存在对地基反力的影响（称为弹性地基梁 “变m法”），据此建立了滑坡体在外力尤其是地震力作用下排架式微型桩组合结构的简化计算公式，并通过实例计算探讨了排架式微型桩组合结构对地震力的特殊反应。

1 计算模型

1.1 模型的建立

排架式微型桩组合结构是把一组一定间距的微型桩用顶梁连接起来，抵抗滑坡推力的一种轻型支挡结构，图1为排架式微型桩组合结构3个单元的平面示意图，其中a，b分别为桩间距和单元间距。图2为图1中排架式微型桩组合结构单元受力示意图和计算模型，其中，虚线为结构受力变形示意线，在该简化模型中将滑坡推力简化为梯形分布的线性荷载，以弹性地基梁理论为基础考虑桩土相互作用。采用拟静力法把地震力以一个突发性常量侧向荷载PH和不平衡弯矩M 的形式施加在最靠近主滑体的1＃桩上，如图2a所示。图2b中，系数ζ1，ζ2根据规范进行取值，γ，b，L分别为滑体重度、单元间距、受荷段高度。

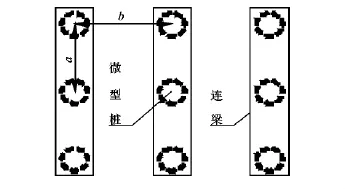
图1 三个排架式微型桩组合结构单元平面示意图

对桩前的抗力，特按边坡的特性和桩前结构的作用来分析确定：正常情况下滑面以上不稳定滑体中已不再适宜按弹性地基梁来考虑，但由于排架式微型桩组合结构单元是由3个微型桩通过顶梁连接组成，它们对滑体的滑动起到一定的约束作用，所以除3＃桩外，1＃，2＃桩作为弹性地基梁来考虑还是可以的，但其桩前抗力的大小因位置和约束力的不同而有所区别，主要体现在m值的变化上。因此，本文在弹性地基梁理论基础上，提出按“变m法”来考虑排架式微型桩的桩土作用。

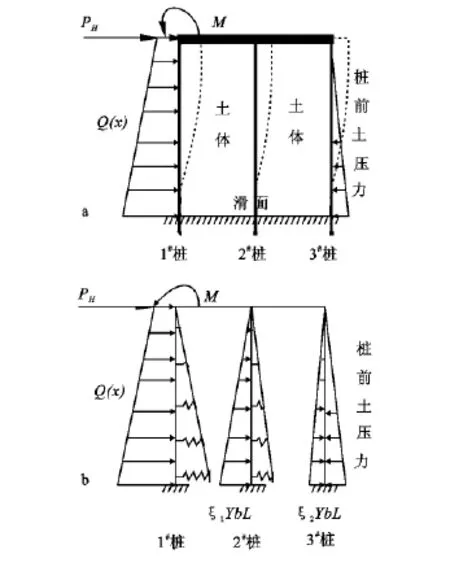
图2 排架式微型桩组合结构受力示意图及计算模型

首先，m值要受到桩间土体抗剪强度的制约，以保证土体不会因被挤出而丧失承载能力，如式（1）所示：

式中：αf——破坏面与大主应力作用面的夹角；τf——抗剪强度；bk——桩的计算宽度；m——地基土横向抗力系数随深度变化的比例系数；x——计算深度；y——桩的挠度；σ3——第三主应力。

其次，考虑边坡特性、组合结构特点和土层特性等对m 值的影响［11－14］，如式（2）所示，然后与各桩的计算公式相结合，计算确定合理的m值［15］：

式中：Hcr，ycr——相应的荷载、位移；vy——桩顶水平位移系数；EI——桩的抗弯刚度。

考虑到桩前滑坡体表面在多数情况下为一倾斜斜面，则桩前土体能够提供的最大土压力要明显小于被动土压力，国外很多试验结果证明了这一点。因此，对于3＃桩前土压力应取剩余抗滑力和“能够提供的土压力”二者中的较小值。在实际工程中，滑面处各桩并未按完全固定端来约束，但由于微型桩所处理的滑坡量级很小，导致滑面处的桩体位移较小，对上部结构的影响不大，所以在此处作为固定端约束来假定，同时滑面以下结构内力暂不作为本文讨论的内容。

1.2 基本假定

按照图2所示的排架式微型桩组合结构及以上讨论，模型计算基本假定如下：

（1）滑面处视为固定端，滑面以下微型桩部分不发生移动变形。

（2）微型桩与顶梁的连接为刚性连接，顶梁视为刚性构件，且顶梁只发生水平位移，没有转动，各桩桩顶处水平位移相等。

（3）滑面以上排架结构承受边坡力系简化为梯形线性荷载。

（4）地震力简化为一个突发性常量侧向荷载PH和一个弯矩M施加在最靠近主滑体的1＃桩位置。

1.3 计算模型分解及公式建立

1.3.1 计算模型分解 通过分析图2b所示模型，可以建立3种基本计算模型，顶梁对桩的影响通过的水平推力P（PH）及弯矩（M）来体现（如图3所示）。1＃桩受力模型可以通过图3a，3b，3c的基本模型组合得到；2＃桩受力模型通过图3b，3c所示基本模型组合计算；3＃桩可根据结构力学理论来进行计算。

图3 基本计算模型示意图

图3中，q1（x）取值为滑坡推力的矩形部分；q2（x）在用于计算1＃桩时，取值为滑坡推力的三角形部分，用于计算2＃桩时，取值为ζ2γbx；（PH）表示如果计算中需考虑地震力，则在P中加入PH。（M）表示根据边坡与组合结构的相对位置，根据实际情况考虑是否存在该弯矩，如果存在就考虑，不存在则不考虑。“（）”表达的意思是根据实际计算需要，选择是否考虑。

1.3.2 公式的建立 由于1＃，2＃桩的计算模型都可以通过基本计算模型组合得到，因此，根据弹性地基梁理论，通过幂级数法建立3种基本计算模型的挠度计算公式，如式（3）所示，然后根据1＃，2＃桩的受力模型，选择需要的计算公式，整合为总挠度y的计算公式。桩的转角θ，弯矩M，剪力Q的计算公式可以通过与挠度y的微分关系得到。

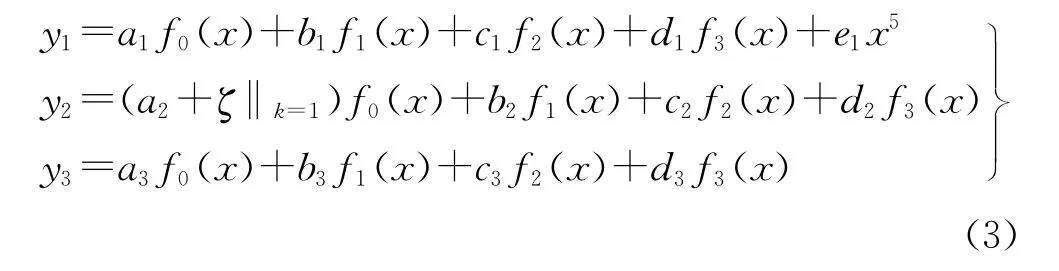
图3所示的3种基本计算模型a，b，c的挠度公式分别与式（3）中的y1，y2，y3相对应，式（3）中ζ＝q2／L。未知系数可以根据其对应的边界条件求得，如式（4）所示（下标0和L分别表示桩顶和固定端）：

其余各计算系数的表达式如下：

2 计算实例

2.1 工程概况

在达渝高速K151＋200松散滑坡体上，在靠近坡脚位置采用多排排架式微型桩组合结构进行加固。该滑坡长约为48m，宽约为60m，深度约为7m，滑面以上主要由人工填土、碎石土构成。经过实际勘测计算把作用在组合结构上的滑坡推力简化为梯形分布的线性荷载，在桩顶和固定端值分别为10kN／m和15.97kN／m。

考虑地震力为突发性常量侧向荷载，地震烈度为8°，根据抗震设计规范，计算出大小约为PH＝160 kN。滑体重心与桩顶高程基本一致，因此不考虑不平衡力矩M的作用。

每根微型桩由3根φ32mm钢筋、套管及混凝土组合而成，排架式微型桩计算单元共采用3根微型桩通过顶梁连接。根据等效原理得到的相应圆形截面的抗剪力为τfa＝［τ］ACS＝788.8kN，其中ACS＝0.006 8m2，为等效截面积。相关计算参数如表1所示。

表1 工程实例计算参数

2.2 地震力对排架式微型桩组合结构影响的分析

对比排架式微型桩组合结构承受的各荷载值大小可以发现，地震力值处于较大的水平，因此特别对比分析了地震力施加前后组合结构的反应，如图4—5所示。

图4 地震力对1＃桩挠度y，转角θ，弯矩M和剪力Q影响对比

如图4所示，地震力对1＃桩的影响主要位于桩顶至3.5m深度范围内，尤其是桩顶位置附近，其挠度及内力值都发生了显著的变化：

挠度值由地震力施加前的0.008 6m，增大为0.038 9m，约为施加前的4.5倍。未施加地震力时转角最大值为0.004 9，施加地震力后，转角值变为－0.008 6，方向上发生了变化。

桩顶的弯矩值由地震力前－15.46kN·m变为23.25kN·m，变化幅度为38.71kN·m。与弯矩的变化相对应，剪力的主要变化也位于桩顶位置，由地震力施加前的26.77kN变为－45.78kN，变化幅度为72.55kN。

图5给出了地震力对2＃桩挠度、转角及内力影响曲线，从图5中可以看出，地震力对2＃桩挠度、转角及内力的影响也主要位于桩顶至3.5m深度范围内，桩顶位置附近最明显，挠度和内力值都有显著变化，但未发生方向的改变。

对比图4可以看出，2＃桩的挠度及内力分布图与1＃桩的分布图有较大的差别，主要因为这2桩的受力及位置不同。在采用排架式微型桩群加固该滑坡的同时，设计并建立了深部位移监测孔和地表位移监测点，通过与监测数据的比较，正常荷载情况下模型计算结果和现场实测结果基本一致，说明模型是有效并正确的，基本上能反映现场的实际情况。

图5 地震力对2＃桩挠度y，转角θ，弯矩M和剪力Q影响对比

3 结论

（1）对不稳定坡体，引用弹性地基梁理论时应满足一定的条件。

（2）借助一般微型桩水平承载力计算思路，通过弹性地基梁“变m法”来体现微型桩前其他桩对地基反力的影响作用，使计算更加合理。

（3）对桩前存在不同约束条件的3根微型桩，分别采用不同的基本计算模型组合，建立了较为完善的排架式微型桩组合结构的计算公式。工程实例计算结果与现场实测结果的一致性验证了本模型的合理性。

（4）区别于刚性支护结构，排架式微型桩组合结构可以利用自身的变形，削弱地震力对边坡稳定的影响，提高工程的安全性。

（5）为减小桩顶变形，必要时可以用横梁或顶板对排架式微型桩组合结构进行连接。

［1］Armour T，Groneck P，Keeley J，et al.Micropile design and construction guidelines implementation manual［R］.Washington D C.U.S.Department of Transportation，Federal Highway Administration，2000.

［2］Shields D R.Buckling of micro－piles［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2007，133（3）：334－337.

［3］Cadden A，Gomez J，Bruce D，et al.Micro－piles：recent advances and future trends［C］∥Current Practices and Future Trends in Deep Foundations.Reston，USA：American Society of Civil Engineers，2004：140－165.

［4］丁光文.微型桩处理滑坡的设计方法［J］.西部探矿工程，2001，13（4）：15－17.

［5］史佩栋，何开胜.小桩的起源、应用与发展（Ⅱ）［J］.岩土工程界，2005，8（9）：15－18.

［6］冯君，周德培，江南，等.微型桩体系加固顺层岩质边坡的内力计算模式［J］.岩石力学与工程学报，2006，25（2）：284－288.

［7］肖世国，鲜飞，王唤龙.一种微型桩组合抗滑结构内力分析方法［J］.岩土力学，2010，31（8）：2553－2559.

［8］周德培，王唤龙，孙宏伟.微型桩组合抗滑结构及其设计理论［J］.岩石力学与工程学报，2009，28（7）：1353－1362.

［9］韩金平.液化场地微型桩基地震响应数值仿真研究［D］.合肥：合肥工业大学，2007.

［10］贺传友.液化场地微型桩基地震响应三维数值分析［D］.合肥：合肥工业大学，2009.

［11］陈正，梅岭，梅国雄.柔性微型桩水平承载力数值模拟［J］.岩土力学，2011，32（7）：2219－2224.

［12］罗红明，唐辉明，胡斌，等.考虑地震力的刚体极限平衡法及其工程应用［J］.岩石力学与工程学报，2007，26（1）：3590－3595.

［13］王念秦，姚勇，罗东海.滑坡综合治理方案比选评价模型［J］.水土保持通报，2009，29（1）：111－114.

［14］严金凯，殷跃平，门玉明，等.滑坡微型桩群加固工程试验研究［J］.土木工程学报，2011，44（4）：120－128.

［15］贾庆山.桩基水平承载力标准值与m值确定［J］.特种结构，1995，12（2）：23－24.