最小树的一种新的生成方法

洪燕君

（石河子大学师范学院石河子832003）

最小树理论是网络优化的一个重要内容，迭代思想是优化理论的基本思想。迭代思想是从一个初始的状态出发，根据判优准则判断该状态是否最优，若不是最优，依据迭代规则进行迭代更新，得到一个优化的状态，继续重复上述过程，直至得到最优解或判断无解。这种思想方法在通讯网、电力网、交通网、管道网、工程进度网、生物信息网等的设计和实际生活中的许多大型优化问题中均有广泛的应用。本文利用判优准则判断任意生成树是否最优，如果不是最优，则利用迭代思想进行迭代，得到权更小的生成树。

许多学者对最小树问题都做了相关的研究，如文献［1－3］介绍了求最小树的常用方法，如Kruskal算法（避圈法）、破圈法、Dijkstra算法等，文献［4］给出了最小树算法的复杂性分析，C Thomassen［5］的最新研究工作表明：图的生成树的数目还和图的无圈定向数有关并得到了无桥无环图的生成树的数目总是不超过其无圈定向数。

本文引入了关于连枝的迭代法和关于树枝的迭代法并给出了从一棵生成树中找最小树的新的方法。这种方法在网络设计中有重要的应用。

1 最小树的基本概念和性质

本文讨论的图均为连通无向有限图，文中未涉及的概念和术语参见文献［6－9］。

无向图G定义为一个偶对（V，E），其中V是指图的顶点集，E是指图的边集合。不含圈的图称为无圈图，连通图的无圈图称为树。在树的任意二个点之间添加一条边，称得到的圈为一个基本圈。

设T是连通图G的一棵树，e（i）是树枝。对应e（i）存在G的割集S（i），S（i）只包括一条树枝e（i）及某些余树枝，且与e（i）的方向一致。称S（i）为G

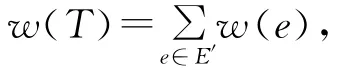
则称w（T）为T的权（或长）。G中权最小的生成树称为G的最小树。

定理1：设T是网络G的一棵生成树，则T是G的最小树当且仅当对任意的边e∈T有，w（e）＝的对应T的一个基本割集。以上定义参见文献［8］。

网络G＝（V，E，W），其中V是指图的顶点集，E是指图的边集合，W是指边的权的集合。

定义1：给定网络G＝（V，E，W），设T＝（V，E′）为G的一棵生成树，令

定理2：设T是网络G的一棵生成树，则T是G的最小树，当且仅当对任意的边e∈T有w（e）＝

从上面定理可得下面定理。

定理3：生成树T是网络G的唯一最小树，当且仅当对于任意的边e∈G＼T，e是C（e）中唯一的最长边。

定理4：生成树T是网络G的唯一最小树当且仅当对于任意的边e∈T，e是S（e）中唯一的最小边。

2 迭代法在最小树理论中的应用

2．1 任意生成树是否为最小树的判断

定理5：设T是网络G的任意生成树，对于每条连枝e′∈G＼T，根据最小树的性质，给出e′的检验数数均为非负数，则该生成树为最小树。

证明：若连枝e′∈G＼T的检验数δ（e′）≥0，说明e′的权在基本圈C（e′）的所有边中是最长边，根据定理1可知：生成树T为最小树。

推论1：若每条连枝边的检验数均大于0，则该生成树为唯一的最小树。

定理6：设T是网络G的任意生成树，对于每条树枝边e∈T，根据最小树的性质，给出e的检验数δ均为非负数，则该生成树为最小树。

证明：若树枝e∈T的检验数δ（e）≥0，说明e的权在基本割集S（e）的所有边中是最小边，根据定理2可知：生成树T为最小树。

推论2：若每条树枝边的检验数均大于0，则该生成树为唯一的最小树。

2．2 利用迭代法求最小树的算法

2．2．1 关于连枝的迭代法（利用连枝的检验数）

该方法的主要步骤为：

1）任给一棵生成树T0。

3）在小于0的检验数中选取最小的，不妨设为e′的检验数最小，则在e′确定的基本圈C（e′）中换进e′，换出C（e′）中的最长边。迭代后得到一棵新的生成树T′，转2）。

由最小树必定存在，则经过有限次迭代后，必会得到图G的最小树。

2．2．2 关于树枝的迭代法（利用树枝的检验数）

该方法的主要步骤如下：

1）任给一棵生成树T0。

2）根据定理6求出所有树枝边的检验数，若全为非负数，则该生成树为最小树；否则，转3）。

3）在小于0的检验数中选取最小的，不妨设e的检验数最小，在e确定的基本割集S（e）中换出边e，换进S（e）中最小边。迭代后得到一棵新的生成树T′，转2）。

由最小树必定存在，则经过有限次迭代后，必会得到图G的最小树。

面对全球气候日益恶劣，雾霾天气频现的情况，大华透雾技术不仅提升了监控感知产品的感知力和稳定性，进一步维护了大众的安全和利益，而且也为雾霾、烟尘、水汽频发的特定场景，筑起了一道视频防控的坚实屏障。

2．3 退化的情形［9］

当关于连枝的迭代法和关于树枝的迭代法中的检验数都是非负数的情况下，若有检验数为0，则表示该网络的最小树不是唯一的，否则，网络具有唯一的最小树，即全部检验数均大于0的情形。

3 实例及分析

例1：判断图1给的生成树T0＝｛e1，e2，e5，e6｝是否为最小树。

图1 生成树和最小树Fig．1Spanning tree and minimal tree

解法一：使用关于连枝的迭代法（利用定理5）。

生成树T0的连枝集为｛e3，e4，e7，e8｝，因而由它们确定的基本圈分别为：

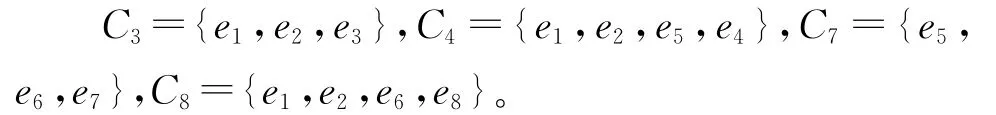
它们对应的检验数分别为：

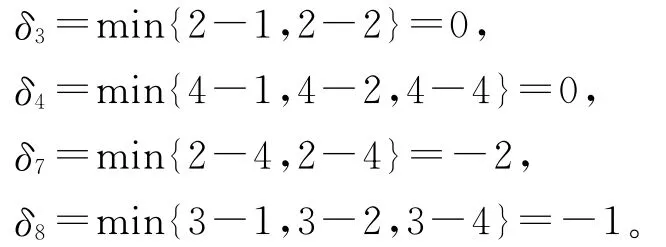
根据定理5可知，该生成树T0不是最小树。

解法二：使用关于树枝的迭代法（利用定理6）。

生成树T0＝｛e1，e2，e5，e6｝，因而由它们确定的基本割集分别为：

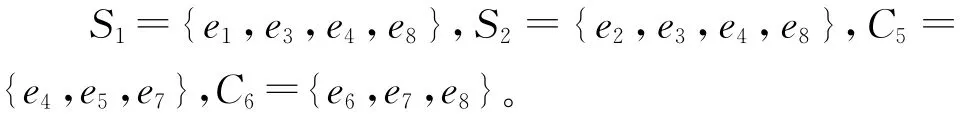
它们对应的检验数分别为：

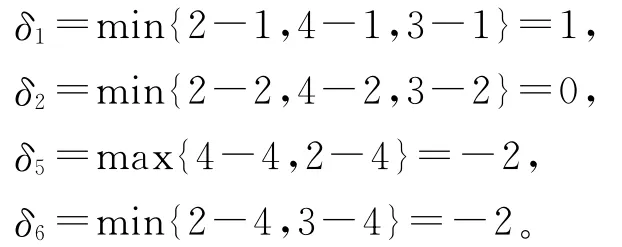
根据定理6可知，该生成树T0不是最小树。

例2：从例1给定的生成树T0＝｛e1，e2，e5，e6｝出发，求该网络的最小树。

解：使用关于连枝的迭代法（利用连枝的检验数）。

由例1可知，e7的检验数最小，故连枝e7应该换入，而树枝e5应被换出。此时，得到一棵新的生成树T1＝｛e1，e2，e6，e7｝（T1的权比T0的权小），然后计算关于生成树T1的所有连枝的检验数。为此求出所有的基本圈如下：

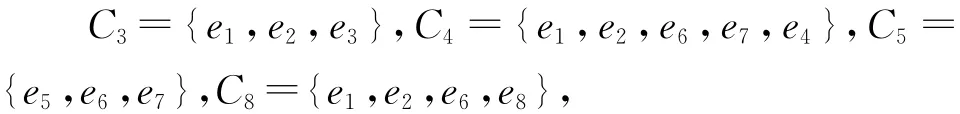
从而它们对应的检验数分别为：

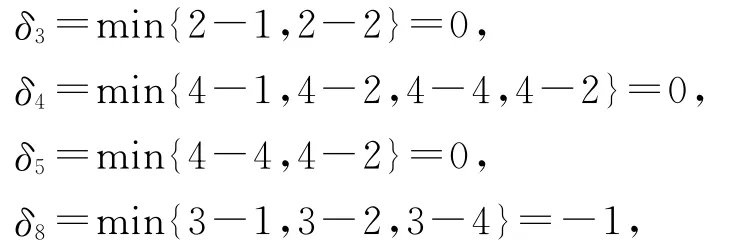
根据定理5可知，该生成树T1不是最小树。e8的检验数最小，故连枝e8应被换入，而树枝e6应被换出，此时，得到一棵新的生成树T2＝｛e1，e2，e8，e7｝（T2的权比T1的权小），然后再计算关于生成树T2的所有连枝的检验数。为此先求出所有的基本圈为：

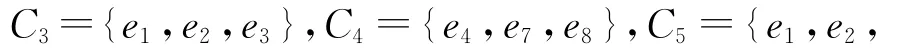
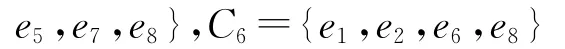
它们对应的检验数分别为：

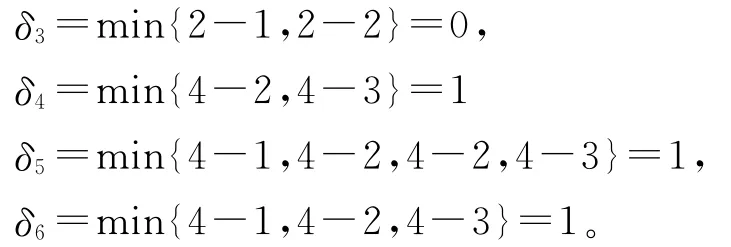
由定理5可知，生成树T2是最小树，且该最小树不是唯一的。

使用关于树枝的迭代法（利用树枝的检验数），并根据关于连枝的迭代法可类似求出最小树。

4 结语

1）本文给出了从一棵生成树中找最小树的新方法。这种方法和网络计划图上优化问题的算法以及一般的组合最优化问题有着比较密切的关系。

2）实际生活中的许多问题都可以转化为最小树问题来求解，并且其算法的复杂性是多项式级别的，如假设要建造一个连接若干城市的铁路网络，并且知道任意二个城市之间的直通铁路的造价时，使用我们的算法就可以设计出一个总造价最小的铁路网络。

3）本文的算法可以生成一棵最小树，并且这棵最小树一般是最优的。

［1］ Kruskal J B．On the shortest spanning subtree of a graph and the traveling saleman problem ［J］．Proc AMS，1956，7：48－50．

［2］Dijkstra E W．A note on two problem in connexion with graph［J］．Numer Math，1959，1：269－271．

［3］Floyd R W．Algorithm 97，shortest path［J］．Comm ACM，1962，5：345－345．

［4］Edmonds J．Path，trees and flowers［J］．Canad J Math，1965，17：449－467．

［5］Thomassen C．Spanning trees and orientations of graphs［J］．J Combinatorics 2010，1（2）：101－111．

［6］胡运权，等．运筹学基础及其应用［M］．4版．北京：高等教育出版社，2004：119－136．

［7］刘家壮，王建方．网络优最优化［M］．武汉：华中工学院出版社：36－79．

［8］田丰．图与网络流理论［M］．北京：科学出版社，1987：15－42．

［9］刁在筠，刘桂真，宿洁，等．运筹学［M］．3版．北京：高等教育出版社，2007：198－203．