沙丘粗糙面的二次极化电磁散射*

刘伟 郭立新 孟肖 郑帆

(西安电子科技大学理学院,西安 710071)

(2013年1月18日收到;2013年2月19日收到修改稿)

1 引言

地球陆地上约五分之一的面积是沙漠.在火星[1]、土卫六[2]等天体表面也呈现和地球沙漠类似的地理构造.沙丘是沙漠地形最主要的组成部分,沙漠地区由于风向的不同和沙粒量的多少,可以形成不同形状的沙丘.常见的有：新月形沙丘、横向沙丘、纵向沙丘和星形沙丘[3].通过研究沙漠地貌的电磁散射对于预报沙尘暴、防沙控沙等工作有着重要的意义.Stephen和Long[4]给出了由倾斜粗糙面元及其面元上的小波纹组成的沙丘表面散射.Nashashibi等[5]在数值仿真和实验测量两方面介绍了不同表面状况干沙的体散射.

由于对探测雷达目标的精细需求,二次及多次电磁散射问题已被广泛地研究[6-8].沙丘的高度显著高于沙漠地面,这样在电磁计算中应该考虑二次散射[9].二次以及多次散射在粗糙面电磁散射的研究中已受到广泛重视.El-Shenawee和Bahar[10]提出了全波法研究二维粗糙表面的多次散射问题,适合粗糙表面的光波散射问题.Ishimaru和Chen[11]对一维粗糙表面的标量波多次散射问题展开研究,提出了简化的多次散射算法.Yoon等[12]采用菲涅耳函数得到衍射和反射系数,结合射线追踪研究了粗糙面散射.Honda等[13]提出了离散射线追踪方法用以研究粗糙面散射.Bourlier和Berginc[14]采用二阶照射函数和遮蔽函数研究了二阶基尔霍夫近似.Xu和Jin[15]采用双向解析射线追踪方法计算了二面角以及海面上舰艇的复合电磁散射.然而尚未见到带有沙丘的粗糙面二次或多次散射问题研究.

本文用单射线追踪得到沙丘粗糙面上二次散射面元,并对散射积分函数进行笛卡尔坐标系矢量分解,以得到二次极化散射模型.第二节仿真了不同类型的新月形沙丘,并介绍了单射线追踪算法的思路和流程;第三节给出了沙丘粗糙面二次极化散射模型;第四节结合数值结果讨论了电磁波入射方向对于沙丘粗糙面极化散射结果的影响;最后给出了相关结论.

2 沙丘粗糙面与射线追踪

风是形成沙丘形状的主要因素.沙粒由于尺寸不同分别以蠕动、跃动和悬浮等方式运动.沙粒的这三种运动状态当然是形成沙丘表面的重要因素[5].另外因为沙粒不能稳定在一个非常陡峭的斜面上,因此一旦沙丘斜面的梯度大于休止角α,沙粒就会滑落,沙丘就会重新改变自己的斜面,直到其梯度足够平滑以致不再发生这种崩塌[16].Miao等[16]将蠕动,跳跃和崩塌这三种主要的风积沙丘基本过程应用于满足高斯函数分布的初始面上,仿真了新月形沙丘表面.取休止角α=34°,图1采取不同的高斯函数的初始面分别仿真了新月形沙丘中的一般沙丘、狭长沙丘、并列双峰沙丘以及前后狭长沙丘.其中图1(a)给出了风向示意图,被风直接吹向的坡面称之为迎风坡,反之则为背风坡,顺着风向将两侧坡面分为左侧坡面和右侧坡面.可以看到沙丘粗糙面是由沙丘和沙漠地面组成的一种特殊粗糙面,而且沙丘明显高于沙漠地面,这样在电磁计算中应该考虑二次散射.

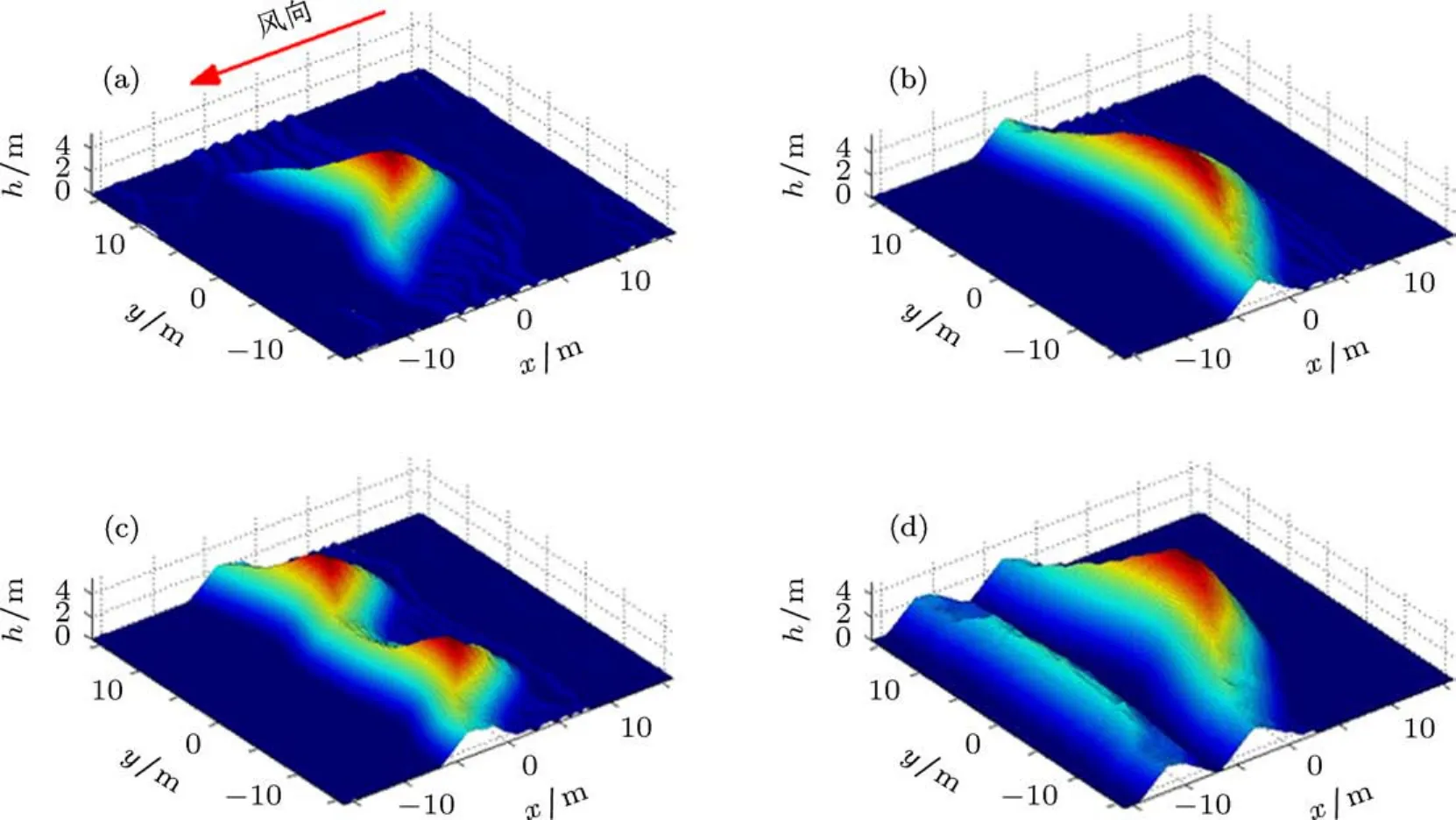
图1 新月型沙丘粗糙面模拟示意图 (a)一般沙丘;(b)狭长沙丘;(c)并列双峰沙丘;(d)前后狭长沙丘

仿真得到的沙丘粗糙面采用MATLAB中的Delaunay剖分很容易得到其三角面元.本文将被电磁波直接照射的面元视作一次散射面元,而由一次散射面元反射的电磁波照射到的面元视作二次散射面元,并采用基尔霍夫近似计算二次散射面元的二次极化散射.为了简化计算量,运用单射线追踪方法,即只考虑面元重心对应的射线,并以此判定遮挡和相交等射线追踪问题,以建立二次极化散射的几何关系.这种简易的单射线追踪方法步骤如下：

1)一次散射面元首先做自遮挡判断,若为暗面元,则标注此面元遮蔽信息为0;

2)一次散射面元若为亮面元,结合入射方向判断是否遮蔽其他面元,其他面元如被遮蔽,则此被遮蔽面元的遮蔽信息记为0;

3)一次散射面元若为亮面元,结合入射方向得到该亮面元的反射矢量,并由此反射矢量和粗糙面做相交判断,若反射矢量与粗糙面相交,相交面元即为二次散射面元,则在二次散射面元位置处保存一次散射面元的几何信息(位置与法向)以备散射计算;

4)遍历所有面元做以上判断操作;

5)计算所有一次亮面元的散射结果与所有二次散射面元的散射结果.

其中遮挡判断包含两部分,分为自遮挡和传播遮挡.步骤1)中的自遮挡判断就是要确定面元是否朝向电磁波的入射矢量.背对电磁波入射方向的面元显然位于阴影区.若面元的外法向和电磁波入射方向的内积满足[15]：

则该面元是可见的,称之为亮面元.否则该面元是不可见的,称之为暗面元.

在步骤2)传播遮挡判断中,需要判断亮面元是否遮挡另一个亮面元.如图2所示,若由r1′处发出的射线为入射电磁波kˆi,其和z轴夹角为θ,在xoy面上的投影和x轴夹角为φ.另一点r2′和r1′的连线与xoy面的夹角为φ.若

则r2′所在的面元被r1′所在的面元遮挡.反之,电磁波将照射到r2′所在的面元.这样三角面元重心的射线追踪显然比三角面元三个端点的射线束追踪简化了很多,在保证一定精度的情况下,能够更快地完成二次散射的几何建模和电磁散射计算.

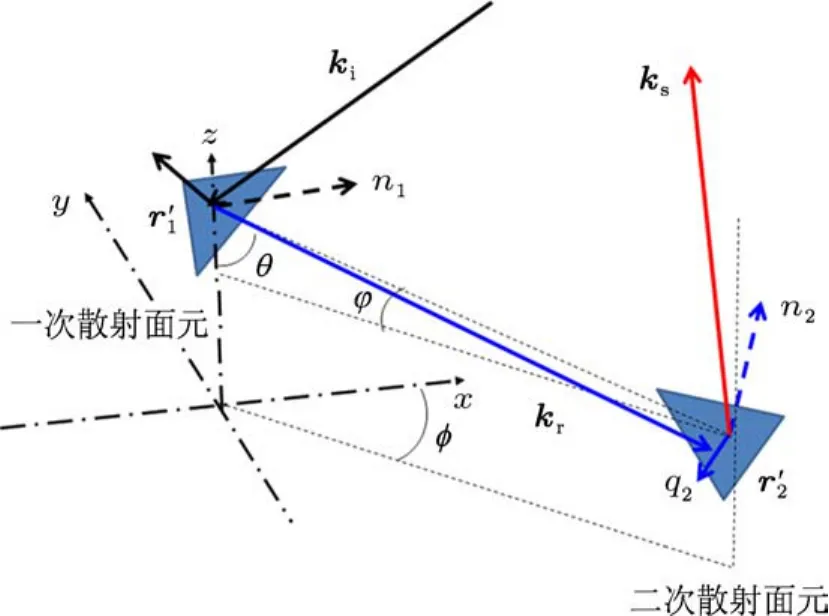
图2 粗糙面的二次散射几何示意图

若将图2中r′1处发出的射线定义为r′1处的反射电磁波ˆki,就可以利用文献[17]中的方法判断其是否与r′2所在的三角面元相交.

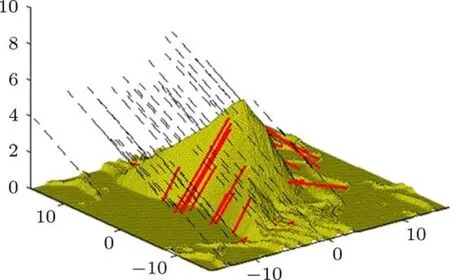
图3 射线追踪效果图

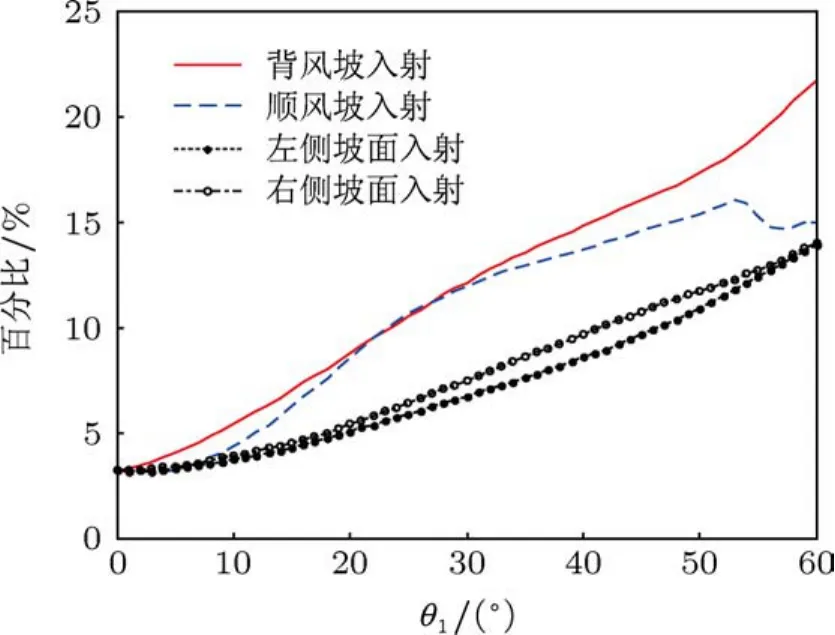
图4 不同入射方向下二次散射面元占面元总数的百分比

图3 给出了本文射线追踪效果图,为了描述方便,每发生200次二次散射取一条射线作图,其中虚线为入射射线,实线为反射射线.可以看到本文采取的方法是可行的.图4给出了不同入射方向条件下二次散射面元占面元总数的百分比,可以看到随着入射角的增大,二次散射面元占面元总数的百分比基本上是增加的.总体而言,背风坡入射时的百分比最大,顺风坡次之,右侧坡面较之左侧坡面在入射角适中区域略大.二次散射面元占面元总数的百分比充分说明了二次散射结果的重要程度.

3 二次散射面元的极化散射

图5给出了沙丘电磁散射的几何示意图,其中入射面垂直于y轴,θ1为入射角,θ2为散射角,θ3为散射方位角.入射场、散射场的正交坐标系分别为(ˆvi,ˆhi,ˆki)和(ˆvs,ˆhs,ˆks),它们与笛卡尔坐标系的关系为

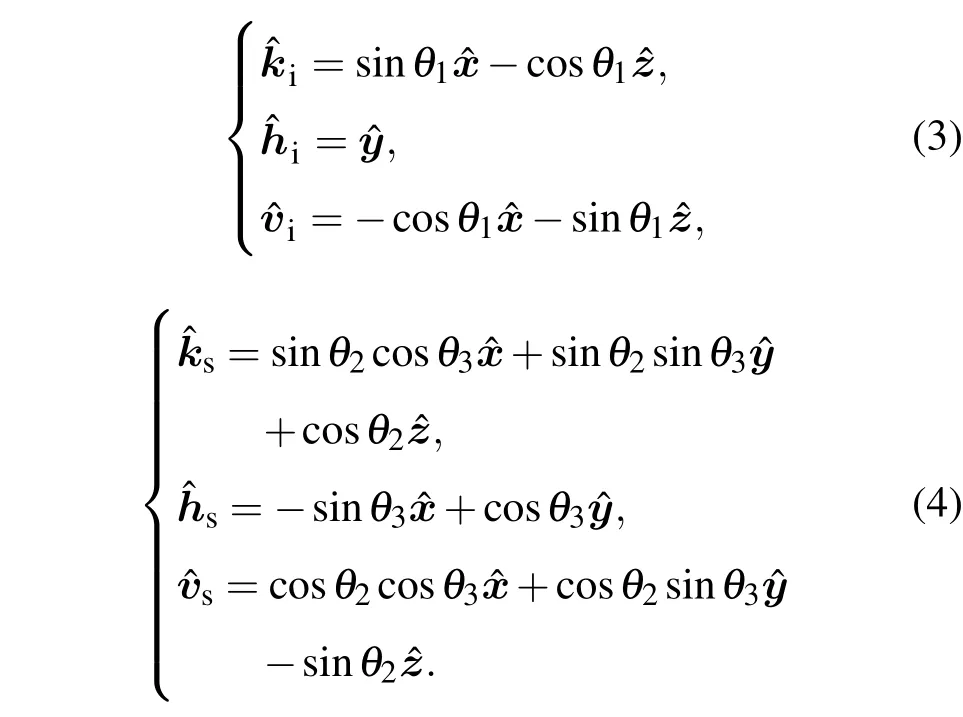
将入射电场分解为平行极化矢量Eih和垂直极化矢量Eiv之和,即

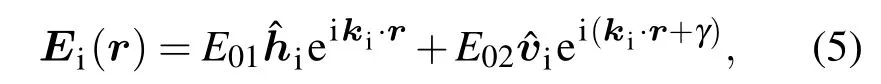
其中ki为入射波矢,γ是Evi分量相对于Ehi分量的相位延迟,E01和E02分别为水平和垂直方向上的电场分量幅值.

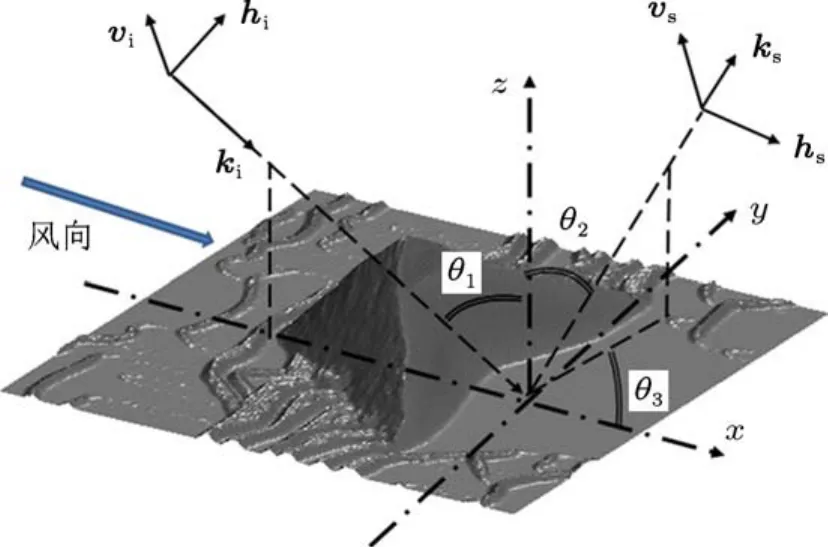
图5 沙丘电磁散射的几何示意图

如图2所示,电磁波入射到一次散射面元r1′,其法线矢量为nˆ1(r′),产生的反射电磁波记为kˆr,kˆr照射到二次散射面元r2′,其法线矢量为nˆ2(r′),并在此产生散射电磁波kˆs.将两个面元的法线矢量定义为

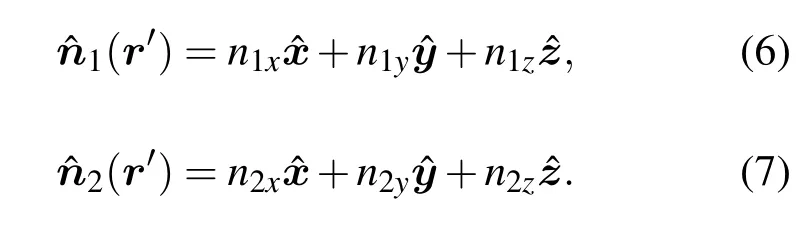
反射电磁波传播方向矢量为

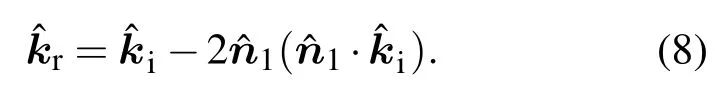
为计算方便,取

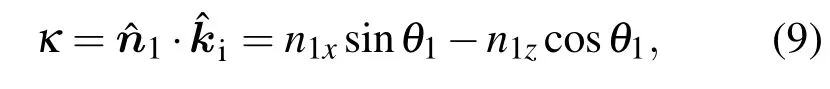
则

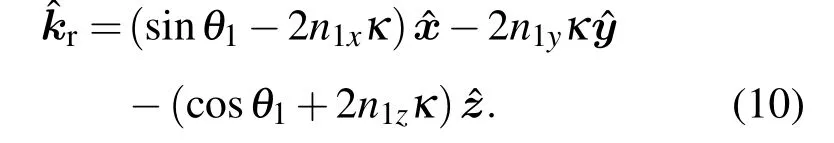
在r1′和r2′处分别定义一个局部正交坐标系(pˆ1,qˆ1,kˆi)和(pˆ2,qˆ2,kˆr),qˆ1和pˆ1是点r1′处的平行和垂直极化单位矢量,以及qˆ2和pˆ2是点r2′处的平行和垂直极化单位矢量,即

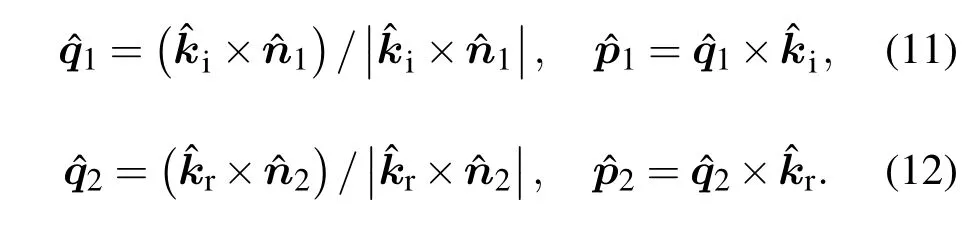
图2中r1′局部坐标系下入射电场的垂直分量与水平分量分别为

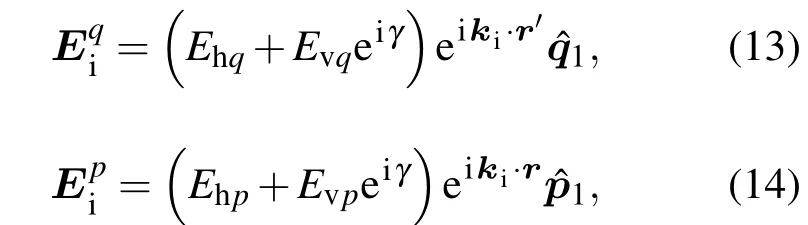
其中各分量幅值

此局部坐标系下反射电磁波两个极化方向上的电场幅值为

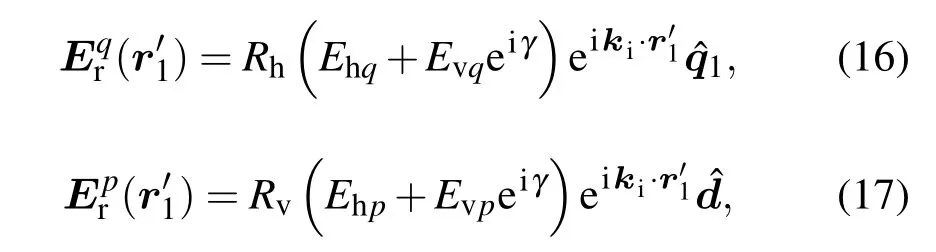
其中Rh和Rv分别为局部(坐标系)中TE和TM极化的菲涅耳反射系数,dˆ=kˆi×pˆ1×kˆr.

根据惠更斯原理,粗糙表面上方任何观察点的散射场都可以由粗糙表面边界上的切向场表示,即

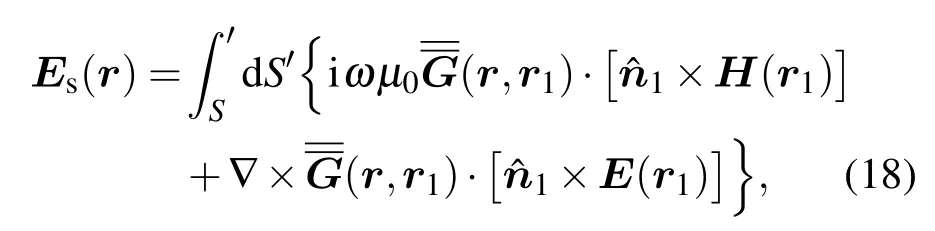
其中S′为进行表面积分的粗糙表面,(r,r1)为自由空间的并矢格林函数.可将此散射场简化为[18]

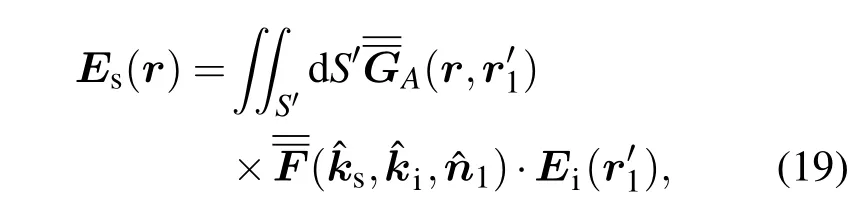
其中

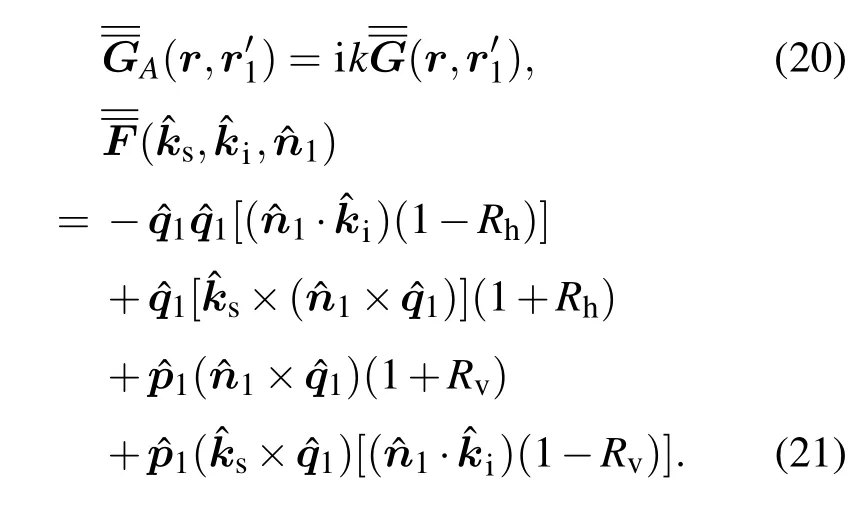
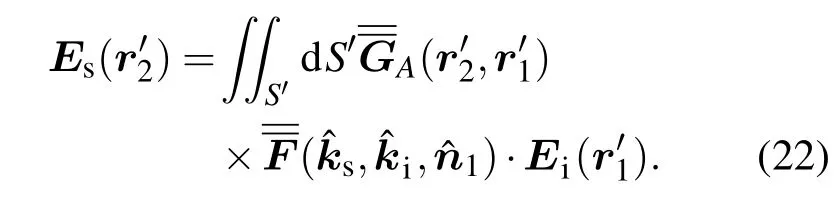
由于射线追踪中的电磁波传播仅考虑了反射,即r2′处的二次入射电场仅考虑来自r1′处的反射电场,则

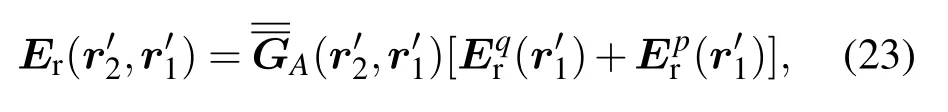
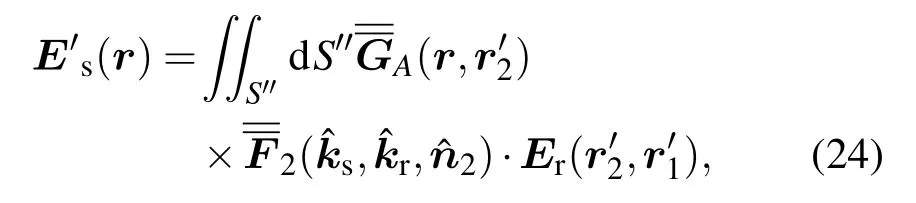
其中

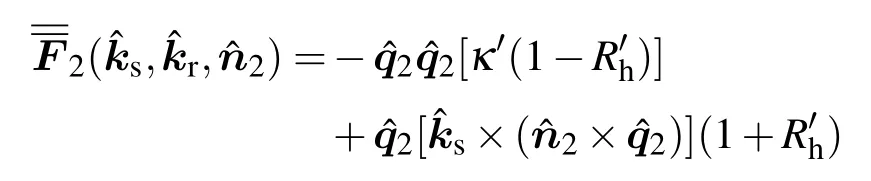
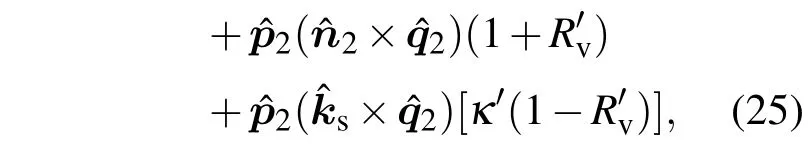
S′为二次散射面元r2′在水平位置的投影,κ′=nˆ2·kˆr,R′h和R′v分别为q2和p2向极化的菲涅尔反射系数,不同的是局部入射角θli由cosθli=-κ′确定.

将(23)式代入到(24)式,可得

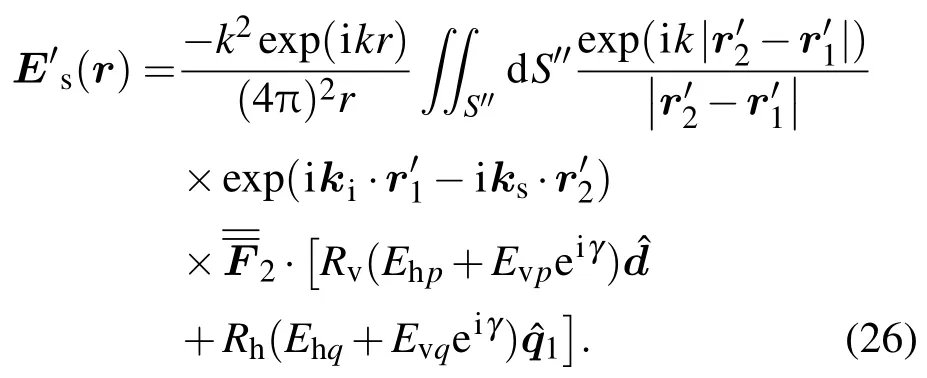
结合入射电场的极化方向,并将总散射场与散射极化方向投影,可得二次散射场的各极化分量

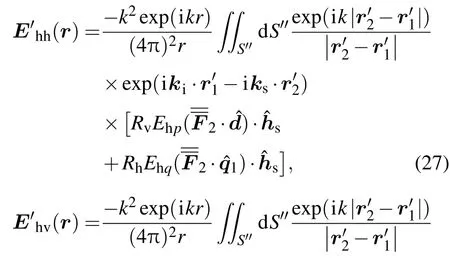
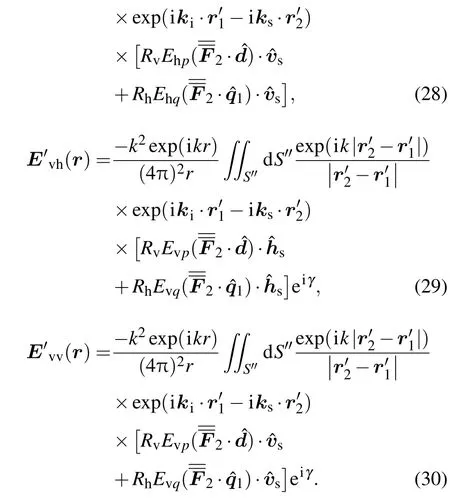
4 数值计算与分析

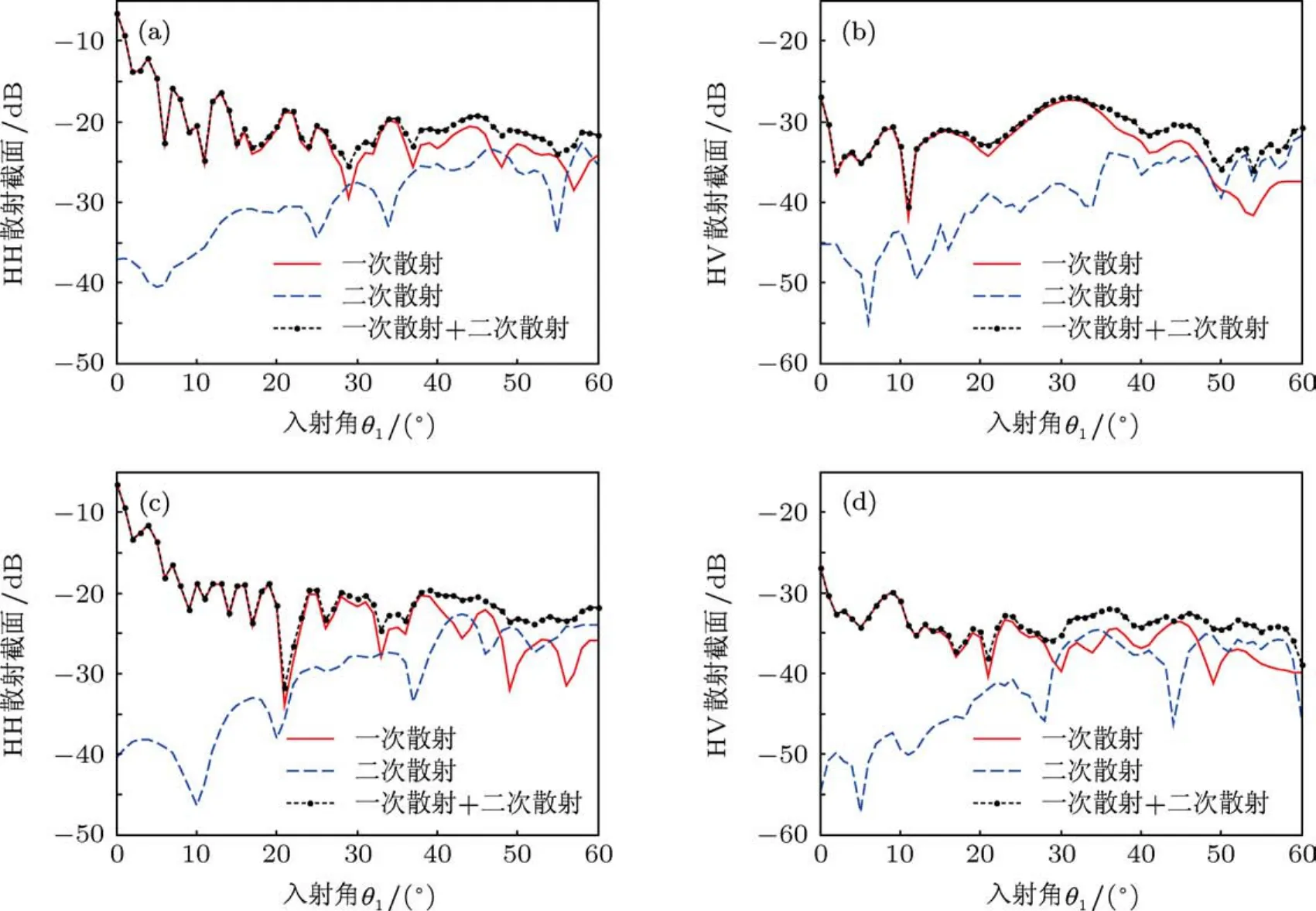
图6 单个新月形沙丘的后向单站极化散射截面 (a)背风面入射HH散射截面;(b)背风面入射HV散射截面;(c)迎风面入射HH散射截面;(d)迎风面入射HV散射截面

以图1(a)中的一般新月形沙丘为例,取入射电磁波频率 f=1.3 GHz,沙丘的介电常数εr=5.1+0.1i[19],采用文献[20]中的方法计算一次极化散射结果,图6给出了电磁波分别沿迎风坡和背风坡入射的后向单站极化散射截面.对比图6(a)—(d)中的极化散射差异,发现HH极化散射中二次散射结果在入射角小于30°的情况下几乎可以忽略不计,而在入射角较大的情况下,由于二次散射面元的增多,可以清楚地看到一次散射结果和二次散射结果之和明显大于仅考虑一次散射的结果.而对于HV极化散射结果,入射角较大时二次散射结果大于一次散射结果.再比较不同入射方向对于总散射场的影响,可以发现图6沿迎风坡和背风坡入射的HH极化散射截面在入射角较小时差异也不大,而当入射角较大时背风坡入射的散射截面大于迎风坡入射,这是因为迎风坡的几何外形向外凸起向两边发散,很大一部分电磁波向两边散射,而背风坡的几何外形向内凹陷,对电磁波有一定的汇聚作用,所以大角度时背风坡的后向一次散射截面要大于迎风坡.

另外可以看到在图6中,当入射角在[25°35°]范围内,后向一次HV极化散射截面出现和同极化一次散射截面相当的较大值,并在与休止角α相一致的34°附近出现峰值,这主要是因为此入射角时沙丘背风面的多数面元局部入射角为0°,而在垂直入射条件下交叉极化等同于同极化.

同图6中的各参数,图7计算了不同入射电磁波方向的双站HH极化散射系数随散射方位角的变化情况.入射角和反射角均为45°,图7中0°与360°皆为前向位置,180°为后向单站位置.四种不同方向入射时的HH极化一次散射结果在前向位置很接近,且较之其他位置最大.背风坡和迎风坡入射时在前向位置的二次散射结果稍大于另外两个方向的结果.因为电磁波朝向背风面和迎风面入射时,被照射区域基本上以入射面对称,所以图7(c)和(d)中的HH极化散射截面曲线基本上以180°为对称.虽然图7(a)和(b)中两侧坡面入射的HH极化散射截面曲线本身并不以180°为对称,但是二者基本上相互以180°对称.可以看到图7(a)中次峰值出现在120°附近,而图7(b)中次峰值出现在240°附近.

图7中四个不同入射方向下在前向和后向之间的中间区域,也就是侧向区域,存在二次散射结果大于一次散射结果的现象.图7(c)和(d)的最大区别在于后向,图7(d)中背风坡后向散射截面在[150°210°]范围方向最大,但是在迎风坡后向大于25 dB的HH极化散射截面的范围较之图7(c)的范围更宽.这也是因为迎风坡的几何外形向外凸起向两边发散,很大一部分电磁波向两边散射,而背风坡的几何外形向内凹陷,对电磁波有一定的汇聚作用.

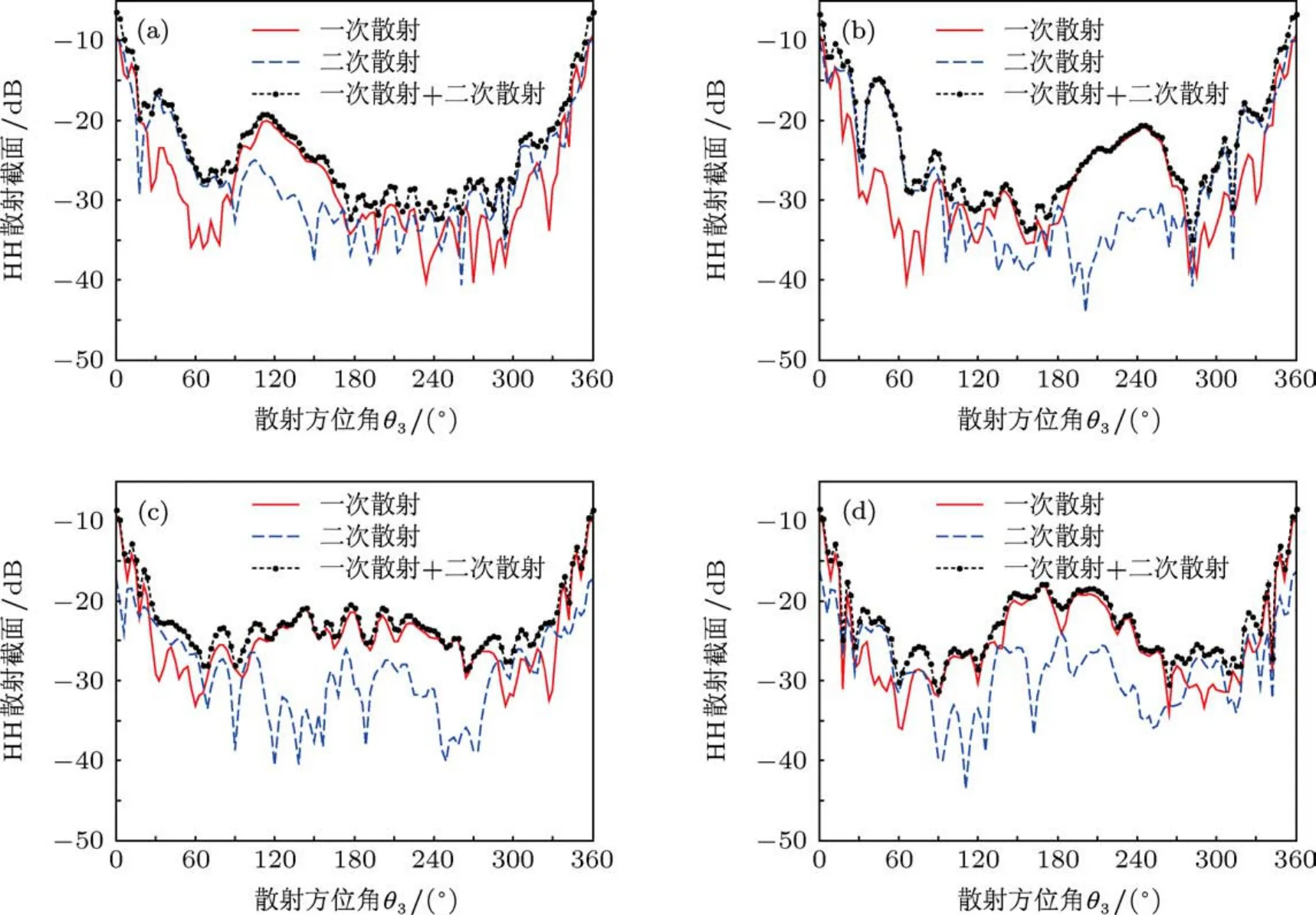
图7 随散射方位角变化的一般新月形沙丘HH散射截面 (a)右侧坡面入射;(b)左侧坡面入射;(c)迎风坡入射;(d)背风坡入射

取以上相同入射频率,图8给出了电磁波照射到图1中四种不同沙丘背风面的包含一次散射和二次散射的全极化散射结果.可以看到同极化散射截面在入射角较小时,除前后狭长沙丘的散射结果较小外,其余三种沙丘的散射结果差异很小,而图8(a)中并列双峰沙丘和前后狭长沙丘的HH散射截面分别在入射角 [35°45°]和 [35°40°]范围内明显增强,在图8(b)中前后狭长沙丘的VV散射截面在[35°40°]范围内,并列双峰沙丘的VV散射截面在入射角35°处以及狭长沙丘在入射角50°处明显增强.

在图8(c)和图8(d)中可以看到,前后狭长沙丘由于独特的地形特点,在背风坡入射方向时在前后两个沙丘间更易形成二次强散射的二面角结构,因此其交叉极化散射截面,特别是HV散射截面在整个入射角范围内相对其余类型沙丘较大,而VH散射截面在入射角度小于10°时相对其余类型沙丘较小,在入射角度大于30°时相对其余类型沙丘较大.又因为粗糙面上二次散射不具备后向单站的极化互易性,因此前后狭长沙丘HV散射截面和VH散射截面之间较大的差异,充分说明对于此类沙丘二次极化散射的重要性.

另外三种沙丘的两种交叉极化散射截面基本上还是相同的变化规律.但三种沙丘的交叉极化散射结果差异较大,一般的新月形沙丘是在35°出现峰值,狭长沙丘是在37°出现峰值,并列双峰沙丘是在34°和44°出现峰值,其中44°的峰值最高.一般而言,并列双峰沙丘的交叉散射截面高于另外两种沙丘的结果.

5 结论

本文在风积沙漠理论模拟新月形沙丘的基础上,结合射线追踪理论和基尔霍夫近似,通过矢量分析研究了新月形沙丘的二次散射问题.数值结果表明二次散射结果在特定的角度范围内有显著影响.在电磁波射向背风坡时可以发现其同极化散射截面在入射角较大时大于其他入射方向的结果,以及入射角在休止角附近时的交叉极化散射截面出现峰值,而这些特点主要是一次散射结果的影响.通过散射方位角变化的双站散射截面的对比可以发现,在大后向(散射方位角[90°270°])可以明显观察到不同入射方向的影响,电磁波射向背风坡时总场的同极化散射结果在散射方位角[150°210°]范围内最大,而在散射方位角120°附近电磁波射向右侧坡面时总场的同极化散射结果最大,在散射方位角240°附近电磁波射向左侧坡面时总场的同极化散射结果最大.在不同类型沙丘相同入射方向的比较中,可以发现沙丘之间的二次极化散射特别突出.我们将在以后研究沙丘场的电磁散射中进一步研究二次极化散射问题.

[1]Parteli EJR,Herrmann H J2007 Phys.Rev.E 76 041307-1

[2]Le Gall A,Hayes A G,Ewing R,Janssen M A,Radebaugh J,Savage C,Encrenaz P 2012 Icarus217 231

[3]Bagnold RA 1941 The Physicsof Blown Sand and Desert Dunes(London：Methuen)

[4]Stephen H,Long D G 2005 IEEETrans.Geosci.Remote Sens.43 238

[5]Nashashibi A Y,Sarabandi K,Al-Zaid F A,Alhumaidi S 2012 IEEE Trans.Geosci.Remote Sens.50 2345

[6]Li Y Z,Shi Q F,Wang Q 2006 Acta Phys.Sin.55 1119(in Chinese)[李运周,史庆藩,王琪2006物理学报55 1119]

[7]Liang Z C,Jin Y Q 2003 Acta Phys.Sin.52 1319(in Chinese)[梁子长,金亚秋2003物理学报52 1319]

[8]Wang X B,Wu Z S,Liang Z C,Zhang Y 2012 Acta Phys.Sin.61 244105(in Chinese)[王晓冰,吴振森,梁子长,张元2012物理学报61 244105]

[9]Karnieli A,Cierniewski J2001 Adv.Space Res.28 171

[10]El-Shenawee M,Bahar E 1996 Rev.Proc.Appl.Comput.EM.1 205

[11]Ishimaru A,Chen JS 1990 J.Acou.Soc.A 88 1877

[12]Yoon K Y,Tateiba M,Uchida K 2001 IEICE Trans.Electron.E84-C 267

[13]Honda J,Uchida K,Yoon K Y 2010 IEICETrans.Electron.E93-C 39

[14]Bourlier C,Berginc G 2004 Waves Random Media 14 229

[15]Xu F,Jin Y Q 2009 IEEETrans.Antennas Prop.57 1495

[16]Miao T D,Mu Q S,Wu SZ 2001 Phys.Lett.A 288 16

[17]Moller T,Trumbore B 1997 J.Graphics Tools2 109

[18]Ren Y C,Guo L X 2006 Syst.Eng.Electron.Technol.28 495(in Chinese)[任玉超,郭立新2006系统工程与电子技术28 495]

[19]Fornaro G,Serafi no F 2006 IEEE Trans.Geosci.Remote Sens.44 3497

[20]Liu W,Guo L X,Wu ZS2010 Chin.Phys.B 19 0741021