V-N共掺纤锌矿ZnO光催化性质的第一性原理研究*

桂青凤 崔磊 潘靖† 胡经国‡

1)(扬州大学物理与科学学院,扬州 225002)

2)(宿迁学院,宿迁 223800)

(2012年10月30日收到;2012年12月10日收到修改稿)

1 引言

ZnO是一种新型的II-VI族宽禁带化合物半导体存材在料于.自由然于界其中稳、定较的高物的理激化子学束性缚质能、(无6 0毒 m、eV大)量和室温下较宽的禁带宽度(3.37 eV)等优良特性,被认为是下一代紫外和蓝光发射的光电子器件和显示光电子材料[1],并在发光二极管、紫外探测器[2,3]、太于阳Zn能O电的池光等催领化域剂具[4有]由广于泛能的有应效用地前光景解.最有近机,酸基,杀除细菌,对环境治理和污水清除起着很好的促进作用,引起了人们的广泛关注[5,6].然而,由于ZnO比较大的带隙,对太阳光的吸收主要集中在紫外区域,仅占太阳光的5%,光催化活性也仅表现在紫外光照射的情况下,为了减小ZnO的带隙,充分吸收可见光,人们进行了多种尝试[7],其中,掺杂是一种切实可行的方式.实验表明：Cr,Cd,Cu[8-10]等金属掺杂ZnO后,在可见光区域光催化活性增强;研究发现N,S,C等非金属掺杂的ZnO也出现了可见光区域光吸收增强的现象[11-16],并且一定浓度的掺杂物能减少电子-空穴的复合,从而提高其在紫外-可见光照射下的光催化效率.然而,金属掺杂和非金属掺杂都存在一定的不足,比如金属掺杂容易形成金属团簇,使得体系出现不稳定相,而非金属掺杂中,由于其溶解度低、电离能高等原因,很难实现ZnO的非金属掺杂[17].

此外,单掺杂的ZnO在带隙间生成的杂质能级虽然减小了体系的带隙,但容易俘获光生载流子,对弱于了深体能系级的而催言化,活则性充.当而了阴电-子阳离-空子穴共复掺合的中形心式,削能大阳幅离度子提所带高体的系正的负稳电荷定之性间[18强-2烈0],的这库主仑要相是互由作于用阴,同时可以有效地抑制电子-空穴的复合而不影响体系带隙的减小.

TiO2作为一种常见的光催化剂,无论实验还是理论上都有非常深入的研究[21-23],最近有报道显示TiO2中V-N共掺使得TiO2的光吸收边有效地发生红移[24],并且在可见光照射下,其光催化活性大幅度增强.ZnO与TiO2具有许多类似的性质,比如相似的禁带宽度、导带和价带的带边位置等,但是其电子迁移率是TiO2的10—100倍,从而有比较低的电阻和比较高的电子输运效率,所以其作为光电化学器件,性能要优于TiO2[25].实验上对于ZnO中单掺杂V和N都有相应的报道,比如,通过调节V掺杂的浓度,可以有效地改变ZnO的带隙,使其光吸收的范围发生变化[26];通过改变退火时间,可以有效地提高N掺杂的浓度,使其对可见光的光响应得到大幅度的提高[27].然而,关于V-N共掺的情况,相关报道尚比较少.对V-N共掺情况下的电子能带结构和光学性质的研究将有助于人们对基于ZnO的光催化剂机理的认识和理解,促进光电化学材料的进一步应用和发展.本文采用第一性原理的密度泛函理论研究了V-N共掺的ZnO的电子能带结构、态密度和光学性质,并与V,N单掺杂的ZnO体系进行了对比.结果表明：V-N共掺的体系无论结构的稳定性还是光吸收方面都较单掺杂的体系有了很大的提高,其光催化活性也有相应的提高.

2 理论模型与计算方法

2.1 模型构建

钎锌矿结构的ZnO属于P63mc空间群,对称性为C6V-4,晶格常数a=b=0.325 nm,c=0.521nm,α=β=90°,γ=120°,其中 c/a 为 1.60.本文采用了2×2×2的32个原子的超晶胞模型,V,N原子单掺杂即V,N原子分别取代Zn原子和O原子的位置,形成6.25%的掺杂浓度,由于电子和空穴之间的强烈的库仑相互作用,V-N以电子对的形式占据相邻的晶格位置,替代位置如图1所示.在计算电子和光学性质之前,首先对各种掺杂的ZnO进行了几何优化,以获得最优结构.

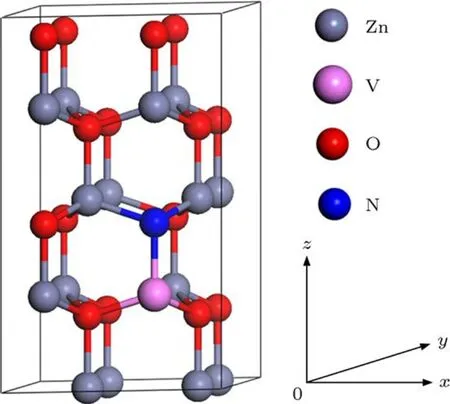
图1 ZnO(2×2×2)超晶胞模型图

2.2 计算方法

本文主要基于密度泛函理论(DFT),采用Materials Studio程序包中的CASTEP软件包[28],以超软赝势(ultrasoft pseudopotential,USP)来描述离子实与价电子之间的相互作用势,应用广义梯度近似(GGA)方法处理电子-电子相互作用,并采用了Perdew,Burke和Ernzerhof(PBE)所提出的关联梯度修正泛函.使用数值化的原子轨道作为基矢,基函数采用双指极基组(DNP),迭代过程中收敛精度为每原子2×10-5eV,原子间的相互作用力的收敛精度为0.03 eV/A˚,晶体内应力收敛精度为0.05 GPa,原子的最大位移收敛精度为10-3A˚,平面波截断能量为Ecut=380 eV.总能量和电荷密度在对全Brillouin区的积分计算采用k点网格为4×4×2的Monkorst-Park方案.

3 结果与讨论

3.1 电子结构分析

为了更好地比较单掺杂和共掺杂的情况,本文首先计算了未掺杂的ZnO,V,N单掺以及V-N共掺的ZnO的能带结构和态密度,计算结果如图2所示.图2(a)表明,对于纯的ZnO而言,价带主要由两部分组成：-4—0 eV主要是O的2p态决定,-5.8—-4 eV主要来源于Zn的3d态,导带底附近的主要成分是Zn的4s态,计算得到的带隙值Eg为0.81 eV,比实验值低很多,这主要是因为GGA方法在计算过程中过高地估计了Zn-3d的能量,使得Zn-3d与O-2p杂化增强,结果价带宽度增大,而带隙普遍偏低.但这并不影响对体系的电子结构的分析.

当V掺杂ZnO时,如图2(b)所示,费米能级向上移到了导带处,材料显示出n型金属的性质,其中-8.6—-6 eV主要是Zn-3d态的贡献,-6—-2.5 eV主要是O-2p态的贡献,由于V掺杂,其3d态跨跃了费米能级,主要体现在-1—2.5 eV区域,V-3d的最低占据态与费米面之间的宽度约为1 eV.此外,与未掺杂的ZnO相比,占据态中出现了Zn-4s态和少量的O-2p态.因此,在光照下,电子将很容易从占据带跃迁到非占据带,在波长较长的可见光区域出现较强的光吸收.

图2(c)表明N掺杂的ZnO体系中,杂质带主要集中在-1.8—0.2 eV,由于O-2p态和N-2p态之间比较强的杂化作用,体系价带位置相对于纯ZnO上移,带隙减小为0.49 eV,电子从价带跃迁到导带需要的能量较小,光吸收将向能量低的区域偏移并且可见光区域光吸收增强.

V-N共掺杂ZnO的体系,如图2(d)所示,与V单掺类似,V-3d态仍然是部分占据,占据态出现了Zn-4s态,由于同时掺杂了N原子,O-2p,N-2p态也出现了占据态.因此,在费米面附近,带内及带间的电子跃迁更加频繁,光照情况下,电子从占据带跃迁到非占据态变得更加的容易,可见光区域的光吸收进一步增强.从电子结构上可以推断出V-N共掺的ZnO在可见光吸收的增强程度上都比V和N的单掺杂提高很多.

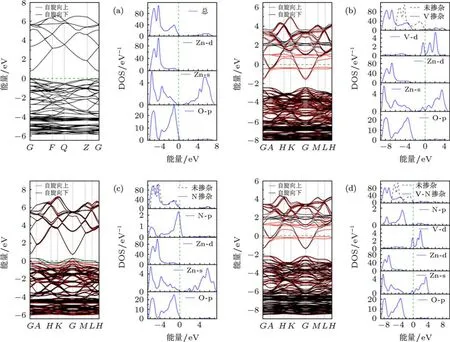
图2 能带和态密度图 (a)未掺杂的ZnO;(b)V掺杂的ZnO;(c)N掺杂的ZnO;(d)V-N共掺杂的ZnO

3.2 光学性质分析

为了进一步分析三种不同掺杂体系的光学性质,我们系统地计算了体系的介电函数和光吸收率.根据量子力学理论,其吸收光谱取决于电子态密度.(1)式给出了介电函数虚部,其中u是电场极化矢量,k是倒格矢,c和v分别代表导带和价带,ω是入射光频率：

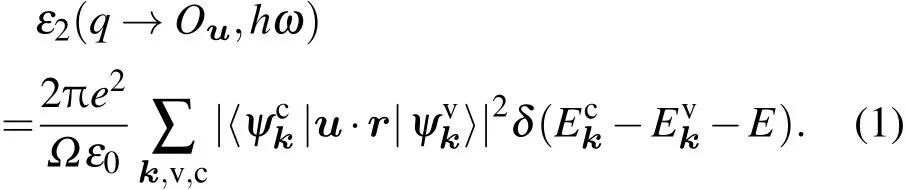
由Kramers-Kronig(K-K)关系,可以从介电函数虚部得到介电函数的实部,从而得到光吸收系数,如(2)式,其中ε1是介电函数实部,ε2是介电函数虚部,ω是入射光频率[9,29,30]：

图3描述了未掺杂和三种不同掺杂情况下的ZnO的介电函数.对于纯ZnO而言,出现了三个明显的峰值,分别位于1.5,6.4和10.4 eV,其中第一个峰值主要来源于价带顶附近的O-2p态电子与导带底附近的Zn-4s态的电子之间的跃迁激发引起的,第二个峰值主要由价带中Zn-3d态的电子和O-2p态电子之间的跃迁引起的,第三个峰是Zn-3d态和O-2s态之间电子跃迁的影响.在掺杂的体系中,可以看出第一峰的位置变化最为明显,都向能量更低的区域偏移,其中V单掺为0.17 eV,主要来源于导带处的V-3d态电子和Zn-4s态电子之间的跃迁,N掺杂为0.39 eV,是价带顶处的N-2p与Zn-4s态之间的跃迁引起的,而V-N共掺为0.18 eV,主要源于导带内V-3d,N-2p和Zn-4s态电子的带内跃迁;第二个峰主要来源于Zn-3d与O-2p态电子之间的跃迁,因此相对纯ZnO而言,其位置变化不大,特别是N掺杂.而V-N共掺的ZnO,该位置向能量低的方向有一定偏移,其原因是V-3d和N-2p态之间强烈的耦合作用对该区域产生了一定的影响;而第三个峰主要由ZnO本征态,即Zn-3d和O-2s态之间的电子跃迁产生,由于受到掺杂的影响极小,因此,四种不同的体系的位置基本不变.这也就表明,掺杂对光学性质的影响主要集中在能量较低的区域,而能量较高的区域受到的影响极小.

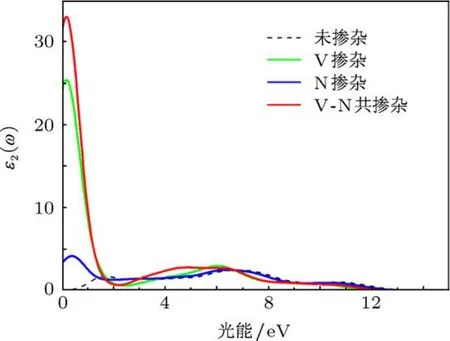
图3 未掺杂,V掺杂,N掺杂和V-N共掺杂ZnO的介电常数

由于计算所得到的ZnO的带隙为0.81 eV,小于实验值3.37 eV,为了能与实验的情况相符,本文采用了scissor近似的方法,其中scissor因子的值为2.56 eV.如图4所示,光吸收仍然集中在紫外区域,但可以发现在低能区域掺杂体系的光吸收率明显加强,其光吸收波长延伸至473 nm,表明可见光区域的吸收在增强,这有利于光催化活性在可见光区域得到提高,对于V,N单掺的体系而言,其计算结果与实验结论基本符合[27,31].其中,V-N共掺的ZnO体系在可见光和紫外光区域的光吸收增强最为明显.进一步表明：V,N单掺杂和V-N共掺杂的体系都可以提高ZnO在可见光区域的光吸收,而V-N共掺的体系被认为是其中最好的光催化剂,由于其在紫外区域光吸收也相对增强,因此,也可推荐作为短波器件,比如紫外探测器、紫外发光二极管.

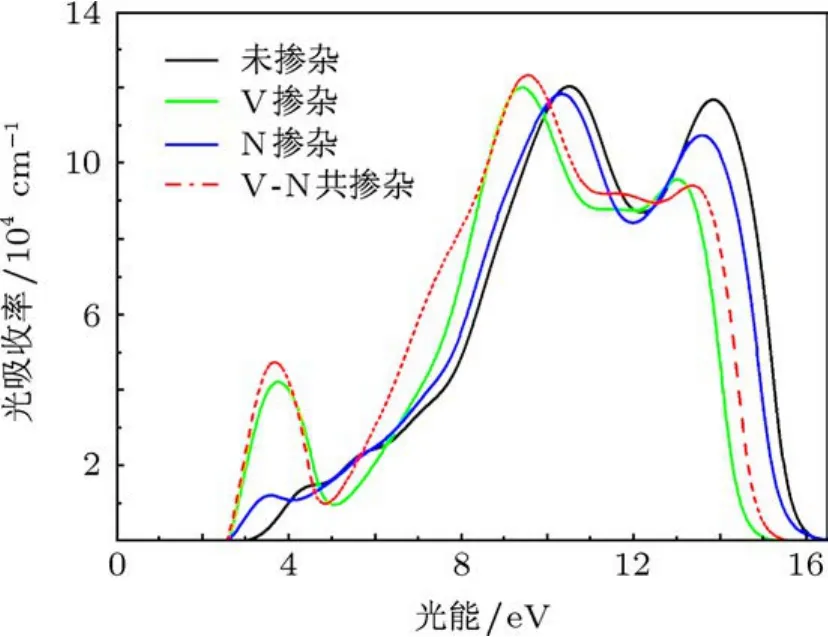
图4 未掺杂,V掺杂,N掺杂和V-N共掺杂ZnO的光吸收率

为了考察这些掺杂体系的结构稳定性,进一步计算了V-N共掺杂体系的结合能,Eb=E(VZn)+E(NO)-E(VZn+NO)-E(ZnO)[32],其中E(VZn),E(NO),E(VZn+NO)和E(ZnO)分别表示V,N单掺和V-N共掺以及未掺杂的ZnO的总能量,最后得到的结合能的值为2.36 eV.正值表示共掺的体系比单掺的体系更加稳定,说明由于带正电的施主电子和带负电的受主电子之间的库仑相互作用有利于阴-阳离子共掺的形式的进行,因此可以大幅度地提高单掺杂的稳定性.

4 结论

本文采用第一性原理平面波赝势方法对比讨论了纯ZnO,V,N单掺杂,V-N共掺杂ZnO的电子结构、光学性质和稳定性.研究结果表明：V-N共掺由于阴-阳离子之间库仑相互作用大幅度提高了系统的稳定性,并且掺杂原子给系统的电子结构和光学性质都带来了很大的影响.由于V-3d,N-2p态以及Zn-4s态的电子之间的带内及带间跃迁,激发了V-N掺杂的ZnO在可见光区域的光吸收增强;此外紫外区域的光吸收也得到了一定的增强,其光催化活性也会得到相应的提高.因此,V-N共掺的ZnO体系可以作为比较好的光催化剂用于清除水和空气中的污染物.同时由于紫外区域的光吸收增强,又可以用作短波光电材料.因此,阴-阳离子共掺的体系能很好地应用于光电化学领域,本文的结果也将为实验和实际应用提供理论参考.

[1]Park T Y,Choi Y S,Kim SM,Jung G Y,Park SJ,Kwon B J,Cho Y H 2011 Appl.Phys.Lett.98 251111

[2]Leung Y H,He Z B,Luo L B,Tsang CH A,Wong N B,Zhang W J,Lee ST 2010 Appl.Phys.Lett.96 053102

[3]Wang G,Chu S,Zhan N,Lin Y,Chernyak L,Liu JL 2011 Appl.Phys.Lett.98 041107

[4]Olad A,Nosrati R 2012 Res.Chem.Intermed.38 323

[5]Wei SY,Wang Z G,Yang Z X 2007 Chin.Phys.Lett.24 800

[6]Hou QY,Zhao CW,Jin Y J2009 Acta Phys.Sin.58 7136(in Chinese)[侯清玉,赵春旺,金永军2009物理学报58 7136]

[7]Sans JA,S´anchez-Royo J F,Segura A,Tobias G,Canadell E 2009 Phys.Rev.B 79 195105

[8]Lai HH,Kuznetsov V L,Egdell R,Edwards PP2012 Appl.Phys.Lett.100 072106

[9]Li L Y,Wang WH,Liu H,Liu X D,Song QG,Ren SW 2009 J.Phys.Chem.C 113 8460

[10]Wu C,Shen L,Yu H G,Zhang Y C,Huang Q L 2012 Mater.Lett.74 236

[11]Chen L C,Tu Y J,Wang Y S,Kan RS,Huang CM 2008 J.Photochem.Photobiol.A 199 170

[12]Shinde SS,Bhosale CH,Rajpure K Y 2012 J.Photochem.Photobiol.B 113 70

[13]Shinde SS,Rajpure K Y 2012 J.Alloys Compd.522 118

[14]Liu W W,Yao B,Zhang Z Z,Li Y F,Li B H,Shan C X,Zhang JY,Shen DZ,Fan X W 2011 J.Appl.Phys.109 093518

[15]Duan M Y,Xu M,Zhou H P,Chen Q Y,Hu Z G,Dong CJ2008 Acta Phys.Sin.57 6520(in Chinese)[段满益,徐明,周海平,陈青云,胡志刚,董成军2008物理学报57 6520]

[16]van de Pol FCM 1990 Cerarn.Bull.69 1959

[17]Ye Y H,L¨u B,Zhang WG,Huang H W,Ye Z Z 2012 Acta Phys.Sin.61 048401(in Chinese)[叶颖惠,吕斌,张维广,黄宏文,叶志镇2012物理学报61 048401]

[18]Hu X Y,Tian H W,Song L J,Zhu PW,Qiao L 2012 Acta Phys.Sin.61 056102(in Chinese)[胡小颖,田宏伟,宋立军,朱品文,乔靓2012物理学报61 056102]

[19]Xie FW,Yang P,Li P,Zhang L Q 2012 Opt.Commun.285 2660

[20]Zhao Z Y,Liu Q J,Zhu Z Q,Zhang J 2008 Acta Phys.Sin.57 3760(in Chinese)[赵宗彦,柳清菊,朱忠其,张瑾2008物理学报57 3760]

[21]Zhang X J,Gao P,Liu QJ2010 Acta Phys.Sin.59 4930(in Chinese)[张学军,高攀,柳清菊2010物理学报59 4930]

[22]Liang P,Wang L,Xiong SY,Dong Q M,Li X Y 2012 Acta Phys.Sin.61 053101(in Chinese)[梁培,王乐,熊斯雨,董前民,李晓艳2012物理学报61 053101]

[23]Wang D Y,Gao SX,Li G,Zhao M 2010 Acta Phys.Sin.59 3473(in Chinese)[王德义,高书霞,李刚,赵鸣2010物理学报59 3473]

[24]Zong Y,Zhao Q 2008 Catal.Lett.124 111

[25]Hendry E,Koeberg M,O’Regan B,Bonn M 2006 Nano Lett.6 755

[26]Wang L W,Meng L J,Teixeira V,Song SG,Xu Z,Xu X R 2009 Thin Solid.Films517 3721

[27]Yang X Y,Wolcott A,Wang G M,Sobo A,Fitzmorris R C,Qian F,Zhang JZ,Li Y 2009 Nano Lett.9 2331

[28]Segall M D,Lindan PJD,Probert M J2002 J.Phys.Cond.Matt.14 2717

[29]Saha S,Sinha T P 2000 Phys.Rev.B 62 8828

[30]Gao G Y,Yao K L,Liu Z L,Li Y L,Li Y C,Liu Q M 2006 Solid.State.Commun.138 494

[31]Qiu Y C,Yan K Y,Deng H,Yang SH 2012 Nano Lett.12 407

[32]Duan X M,Stampfl C,Bilek M M M,McKenzie DR 2009 Phys.Rev.B 79 235208