单拐曲轴TR法镦锻成形过程分析
苌晓兵
(常州机电职业技术学院,江苏常州 213164)
曲轴类锻件TR法单拐镦锻技术由1963年波兰波兹南金属压力加工研究所锻工部T.Rut博士发明,并按发明人姓名的第一个字母命名。其工作原理为:先将棒料车削加工成多个凸台状的坯料,或将坯料分别锻出不同直径的中间坯,然后在专用的镦弯模内将曲臂部分镦出,并将曲柄销错移,弯曲成拐柄[1]。通过肘杆机构,把压力机的压力分解成垂直弯曲分力和水平镦粗分力,力的分配比较合理,能够获得比RR法更大的水平镦粗力。TR镦粗随着肘杆倾角的逐渐减小,水平方向镦粗力逐渐增大,到达镦粗终点时,水平分力最大,其值可达压力机公称压力的1.2倍。水平分力这种变化趋势和曲臂成形阻力的变化规律相吻合。
TR法镦粗曲轴在南车资阳内燃机车厂和武汉重工锻铸有限责任公司得到了应用,并取得了明显的社会经济效益。本文利用ANSYS二次开发的大变形弹塑性有限元分析软件对其变形规律进行研究,分析了水平方向镦粗力和垂直方向错移力的变化规律,并探索了二个载荷同时加载的变形规律。
1 TR法镦锻过程有限元模型的构造
由于曲轴镦锻变形较复杂,为降低镦锻成形过程分析的难度,将其简化成平面变形来分析。采用ANSYS分析大变形问题的方法构造有限元模型,即把模型划分为模具单元、工件单元和接触单元,对工件和模具同时进行分析。工件采用了弹塑性单元,进行了弹塑性分析,模具采用了弹性单元,只进行弹性分析,模拟计算所用有限元模型如图1所示。
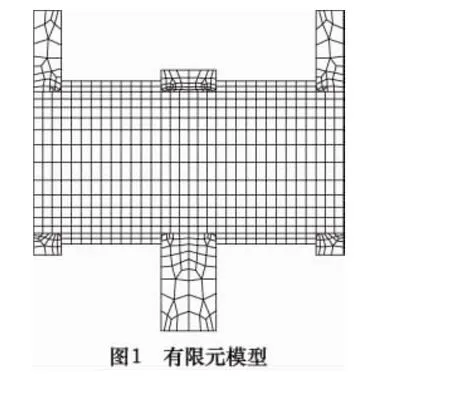
2 TR法镦锻成形过程的模拟
[2]中的ND5曲轴TR镦锻工艺参数,材料选取35CrMoA,坯料尺寸见图2所示。坯料加热温度为1 100℃,模具温度为200℃,在4 500 t水压机上镦锻成形,水压机速度为0.01 m/s,水平镦粗位移60 mm(单边),错移量133.5 mm。模拟过程中考虑了温度的变化,共进行了3次网格重新划分。
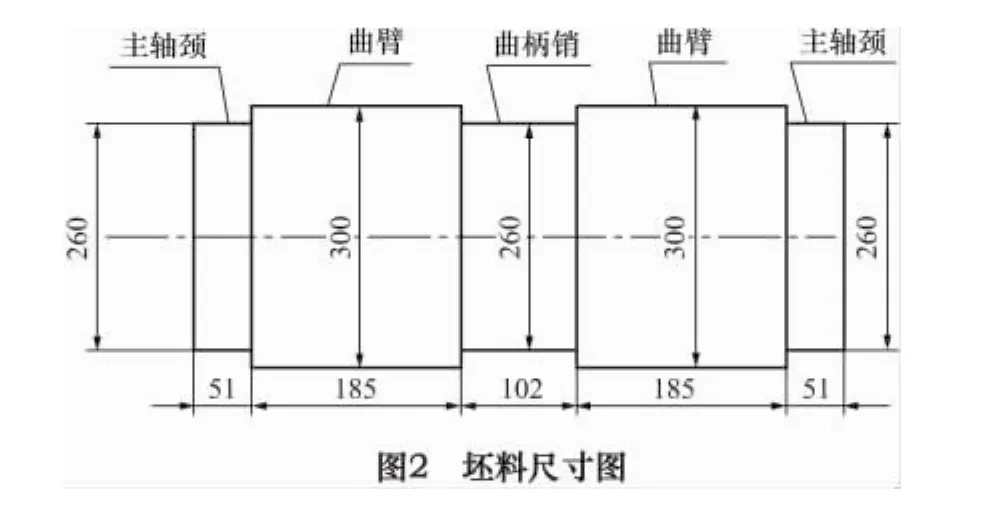
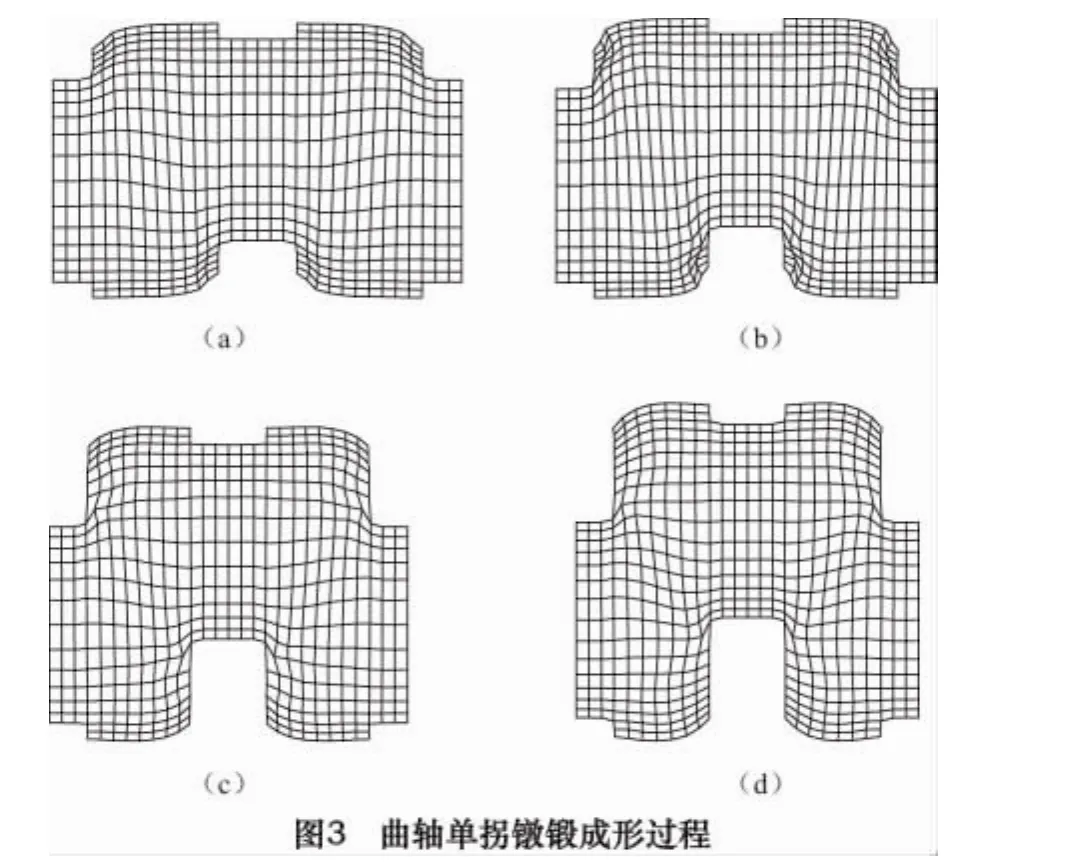
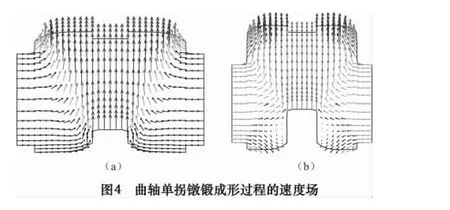
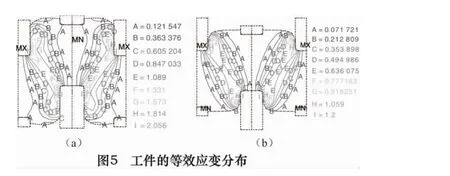
曲轴单拐镦锻成形过程如图3所示。先用模具夹紧主轴颈和曲柄销,使它们不因曲臂镦粗而变粗,模拟中通过施加位移约束实现,然后水平移动夹持主轴颈的模具,镦粗曲臂,同时,夹持曲柄销的模具在垂直方向错移半个曲轴冲程的距离。由于曲臂变形剧烈,而主轴颈和曲柄销基本上没有什么变形,所以在模拟过程中,要对曲臂部分剧烈变形的网格进行重划,保证模拟的精度。曲轴单拐镦锻成形过程的速度场如图4所示,由图4可知主轴颈和曲柄销部分的速度场非常均匀,说明它们只做刚性平移,而曲臂部分的速度场则不均匀,说明曲臂部分变形很不均匀。工件等效应变分布见图5,由图可知变形主要在曲臂部分,曲臂部分变形很不均匀,应变值相差很大,变形集中在施加错移力与对侧被夹紧的主轴颈的连线上,同时向两侧扩展。
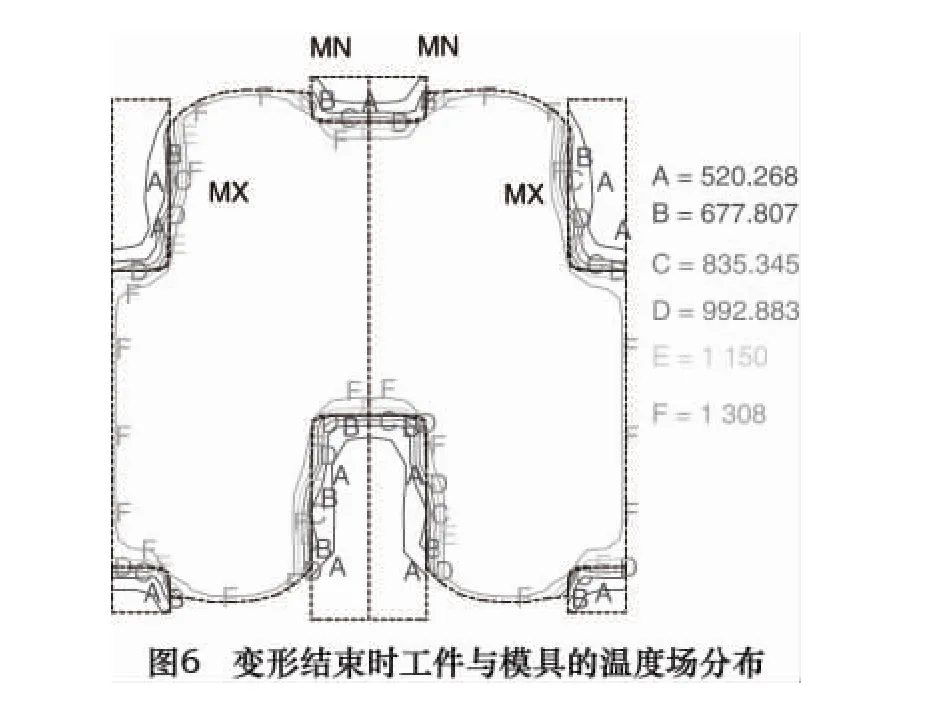
变形结束时工件与模具的温度场分布如图6所示。工件在变形过程中,一方面要与空气进行对流换热和辐射换热,另一方面与模具接触产生传导换热,这两方面导致工件表面温度低、内部温度高,同时工件在变形过程中的塑性功要转化成热能,使得工件的温度又略微上升,变形越大的地方,塑性功转化的热就越多。温度场的变化,直接影响到金属的变形抗力和流动特性,在模拟分析中一定要考虑温度场。由于模具与工件接触产生传导换热,其温度也上升很多。
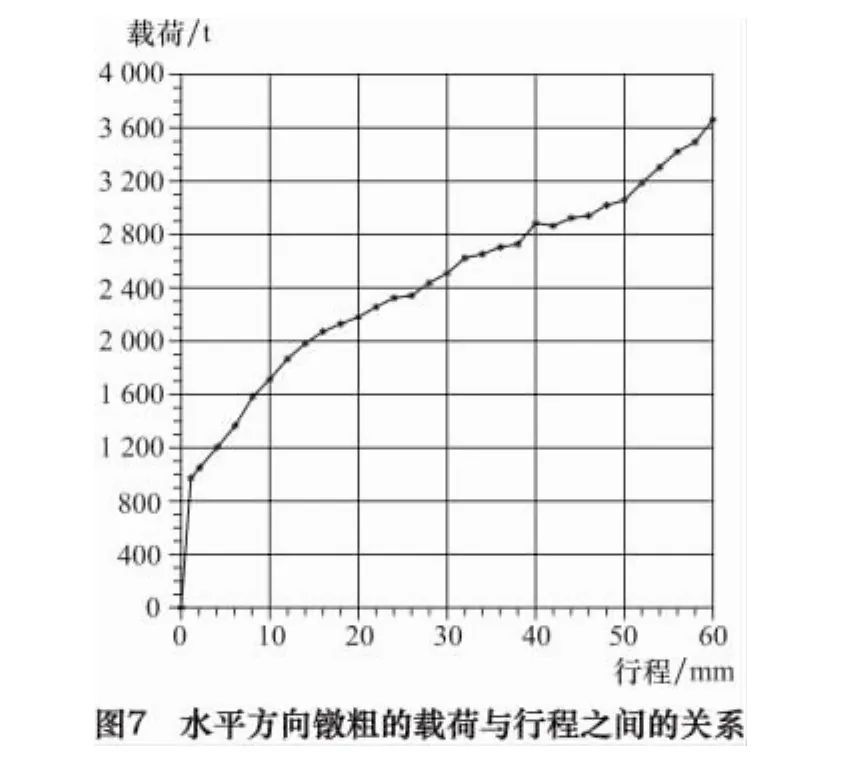
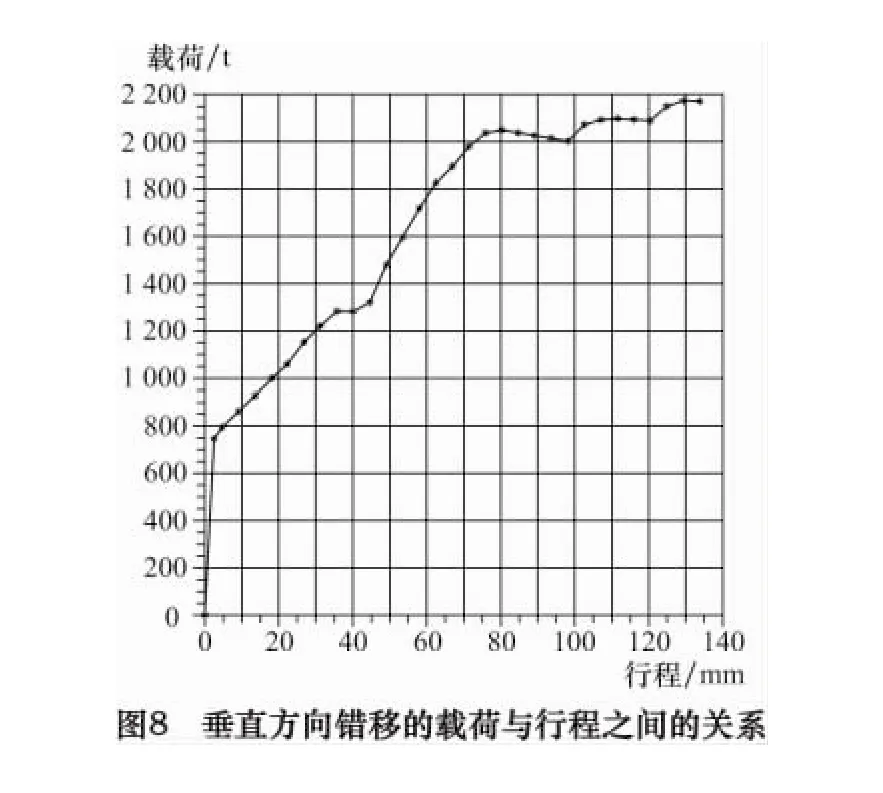
水平方向镦粗的载荷与行程之间的关系如图7所示。水平镦粗位移为0~2 mm时,载荷上升很快,达到1 000 t;水平镦粗位移为2~60 mm时,载荷上升比较缓慢,最后达到3 700 t。垂直方向错移的载荷与行程之间的关系如图8所示。错移量为0~2 mm时,载荷上升很快,达到750 t;错移量为2~75 mm时,载荷上升比较缓慢,达到2 050 t;错移量为75~133.5 mm时,载荷变化不大,最后达到2 150 t。在行程载荷曲线上出现了3处小的振荡,是由于模拟过程中网格重划及决定迭代求解收敛性的失衡力残差引起的[3]。
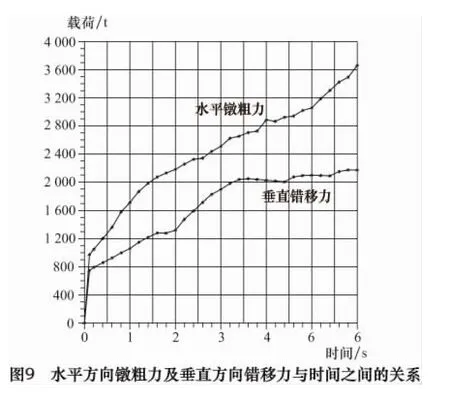
水平方向镦粗力及垂直方向错移力与时间之间的关系如图9所示,水平方向镦粗力总是比垂直方向错移力大。0~0.1 s时,两条载荷曲线基本重合;0.1~3.5 s时,两条载荷曲线上升比较均匀;3.5~6 s时,垂直错移力变化不大,而水平方向镦锻力仍保持0.1~3.5 s时的变化趋势。由图9中的曲线可以看出,在此期间内,水平方向镦粗力与垂直方向错移力的差值逐渐增大,最后差值达1 400 t。
3 结语
通过对曲轴类锻件TR法单拐镦锻成形过程的模拟分析,可以得到如下结论:(1)模拟分析可以获得常规试验方法难以获得的水平方向镦粗力和垂直方向错移力行程载荷曲线、应变场、温度场、金属流动速度场等信息,揭示了TR法单拐镦锻的变化规律,为选取设备,制订工艺提供了理论依据。(2)金属的变形主要在曲臂上,而且集中在施加错移力与对侧被夹紧的主轴颈的连线上,同时向两侧扩展。(3)水平方向镦粗力比垂直方向错移力大得多,选取设备时应考虑水平方向镦粗力,同时兼顾垂直方向错移力。
参考文献
[1]张志文.锻造工艺学[M].北京:机械工业出版社,1983.
[2]夏寅荪.ND5型内燃机车(上)[M].北京:中国铁道出版社,1988.
[3]陈欣如,胡忠民.塑性有限元法及其在金属成形中的应用[M].重庆:重庆大学出版社,1989.

