计及热辐射及翼翅效应的VLGC温度场计算

李小灵，谷运飞

（江南造船（集团）有限责任公司，上海 201913）

0 引 言

VLGC（大型全冷式液化气船），通过内置于货舱区内的A型独立菱形液货舱来容纳温度为-50℃的货物，尽管设有绝缘层，但受内外温差引起的热传递影响，货舱区船体钢结构工作温度比较低。按照IGC（国际散装运输液化气体船舶构造与设备规则）[1]要求，A型液舱的液化气船必须考虑液货舱破损的情况，故在VLGC的设计过程中需根据相关规定进行船体结构温度场计算，并以此为依据选用合适等级的低温钢材。

1 规则要求及计算条件

在进行温度场计算，并以此为依据选择船体结构构件的钢材等级时，除符合船级社一般要求外，还要满足IGC和USCG（美国海岸警备队）的特殊要求[2]。IGC和USCG规定的各个部分的边界温度假定和钢材等级见图1。

进行温度场计算的环境条件须满足以下要求，见表1。

表1 温度场计算的环境条件

图1 边界温度假定

进行计算时该船吃水状态为结构吃水，正常航行工况下，此时的船舶与海水接触面积最大，温度场计算要求最为严格[3]。

对于液货舱绝缘层，其物理特性为：

材料： 喷涂型聚亚胺酯

密度： 35～38kg/m3

20℃时热传导系数： 0.021W/(m·K)

厚度： 约120mm

外层保护： 聚合物表面保护层

除了液货舱绝缘层之外，其他部位的热传导系数均需进行计算来获得。

2 VLGC温度计算分析原理

为了计算船体与液货舱之间的温度分布，需要进行热传递分析。本项分析考虑对流和辐射两种热传导模式，且设定对流传导是沿着液货舱绝缘材料厚度方向进行。

2.1 热传递系数

船体结构的热传导机制主要取决于热量的对流传导和辐射传导。对流传热模式是根据流体的自身特性可分为强制对流和自然对流。通常强制对流发生在流体受外力驱动而产生运动的情况；自然对流则是流体因自身温度场分布不均导致密度不同而产生运动。因此，在船体内部的主要热传递机制为自然对流，而在船体结构外部区域，为空气和海水的运动，其热传导机制为强制对流。

2.1.1 自然对流传热

对流传热是指一个面和流体之间的热传递过程。在自然对流传热中，流体的运动是由固（液）表面与流体之间温度不同而产生的浮力所引起。自然对流传热通常由热分布不稳定所引起。在较冷、较重的流体中温暖、较轻的流体向上运动，流体中的不稳定流线越来越多，导致层流变为紊流。自然对流中边界层的变化取决于流体的浮力和黏滞力的相对数量级。其发生通常与Rayleigh数有关。Rayleigh（Ra）数为Grashof（Gr）数与Prandtl（Pr）数的乘积，如式（1）所示。

Grashof数和Prandtl数由式（2）和（3）定义：

式中：g——重力加速度；β——流体处于膜温度时的容积膨胀系数（K-1）；L——特征长度；ν——流体处于膜温度时的动黏滞率，（m2/s）；α——流体处于膜温度时的热扩散率，（m2/s）；pC ——热容量；μ——动态黏滞度。

则Rayleigh数表示为：

式中：sT——表面温度，（K）；T∞——流体温度，（K）。

大型全冷式液化气船的对流传热必须用无量纲系数进行计算，这些无量纲数包括Nusseult数、Grashof数和Prandtl数，Nusseult数用于衡量表面发生的对流传导，它是Rayleigh数的函数。对流传热系数与Nusseult（Nu）数之间的关系可以表示为：

式中： h——对流传热系数（W/m2·K）；k——流体处于膜温度时的传导率（kcal/mhK）。

对流传热系数可以通过对 Nusseult数的定义来获得。在自然对流传热中，Nusseult数通过一个对Rayleigh数和Prandele数的函数来定义，如式(6)所示：

在各种不同情况下Nusseult数的经验表达式如表2所示。

表2 Nusseult数经验公式

计算自然对流系数时需要特征长度值，特征长度值根据对流产生的方向取为一块板的高度或宽度，如表3所示。例如，对于一个竖直的平面，该值通常为板的尺寸，但在加筋的一面，它是扶强材的间距。对于一块水平板未加筋的面，特征长度为面积除以周长。

表3 对流传热系数

LPG、空气和海水的物理特性如表4所示：

表4 LPG、空气、海水的特性

2.1.2 热辐射

在船体内部空间，由于板架之间温度差异引起的辐射传热与自然对流传热类似。通常情况下，热传导中的自然对流传热是波动的，但是辐射传热随着板架之间温度差加大而上升。为获得船体结构温度的定量结果，计算中需要考虑辐射传热的影响。在本项计算中，考虑了板架之间以及船体与外界空气之间的辐射传热，用式(7)定义辐射传热的相当热传导系数：

式中：1T、2T——相对辐射面开氏温度，K；0T——流体空间温度，K；σ——Stefan-Boltzmann常数，5.669×10-8W/m2K4；tε——有效发射率；12aaF-——辐射面之间外形系数。

辐射外形系数12aaF-表示从离开a1表面到达a2表面的辐射能量比例。对于箱型封闭空间，可以简化为两个对应面，并可进一步简化为无限长度的平行平面。

单个表面的有效发射率的典型数值可以假定为：1) 带涂层的压载舱表面：0.66；2) 铝箔保护的液货舱绝缘：0.20；3) 涂装后的干舱：0.90。

对于两个相对面之间的热辐射传递，有效发射率可以根据式(8)计算：

总的热传递系数为对流、辐射和传导之和。在计算中，传导是最小的一部分，可以用翼翅因子或者是穿入某个空间钢质边界的横截面积或有义厚度来表示。对于浸没在海水中的外板部分，由于大量热量传入海水，该值比较高，同时会随着航速上升而增大。处于航行状态时，对外底板和湿舷侧，总的传热系数约为300W/m2K。当处于停靠港口状态时，该值比较小，外底板约为80W/m2K，湿舷侧约为160W/m2K。对于装载于带有绝缘层的独立液货舱中的货物，总传热系数一般约为300W/m2K或更大，周围的钢结构将趋于与货物温度一致。

2.1.3 翼翅效应

在船体结构中，所有舱室的板均设置纵向和水平加强筋作为加强。这些扶强材会导致钢质板架的热流量上升，即翼翅效应，见图2。加筋表面的热传递用翼翅效率来表示，该无量纲常数平均值通常取为0.8。对流传热的热传递系数可以用翼翅效应进行修正：

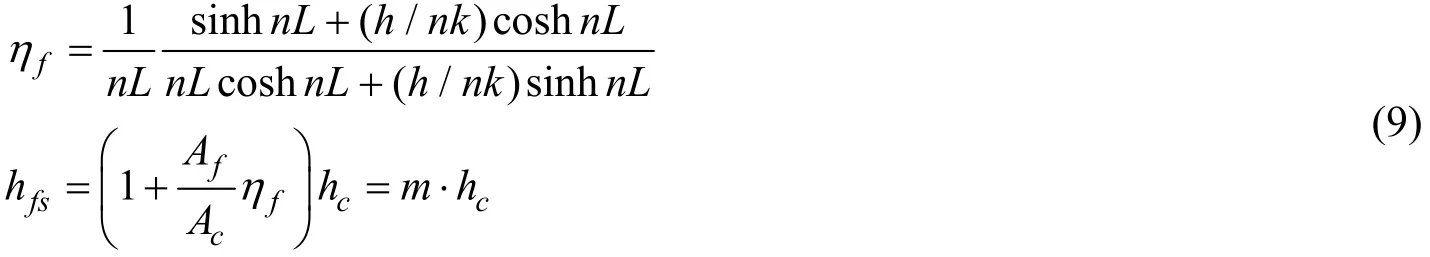
式中： hfs——考虑翼翅效应修正后的对流传热系数； hc——初始对流传热系数； Af——加强筋表面积；Ac——平板表面积；ηf——翼翅因子。

图2 加筋表面的热传递

2.2 热平衡计算

在平衡状态下，进入某个空间的总热量和释放的总热量应该是相等的，以维持其热平衡的稳定状态，见图3。在计算各个板架的相当热传递系数后，某个空间内的温度可以通过热平衡方程来表示：

式中：iA——第i块板的面积；iT——第i个外部空间的温度；0T——内部空间未知温度；ih——相当热传递系数。

图3 空间内的热平衡

相当热传递系数hi反映了多种热传递模式，本计算中主要为对流和辐射。该系数可以表示为：

式中：jk——热传导率；0h——内边界壁每边的对流传热系数；jt——第j块板的厚度；m——考虑加强筋的翼翅效应后的修正因子；rh——第j块板的热辐射引起的对流传热系数。

对于热传导率，通常选取值为： 钢铁：64.0（W/m·k）；绝缘层：0.021（W/m·k）。

为计及USCG以及USCG 阿拉斯加水域5节风速计算条件的影响，引入强制对流传递系数，见图4，表示为7.2V0.78，其中V为风速，单位m/s，量纲为W/m·K，将其加入到自由对流传递系数，值为3.5W/m·K，范围未暴露的甲板区域以及舷侧部分未被静水或波浪浸没的区域。

对流传热系数h的计算主要受制于周围物体、流体和温度等影响热传导性能的因素，该计算花费时间较长，基于对精度的实际要求，对于外部大气、内部空气以及海水的对流传热系数的计算需先假定各体积温度，通过数次迭代计算，直至计算值的偏差达到一定计算精度，则计算结束。

2.3 钢板温度计算

通过计算所得的空间内部温度，可以计算出每块钢板的温度，见图5。

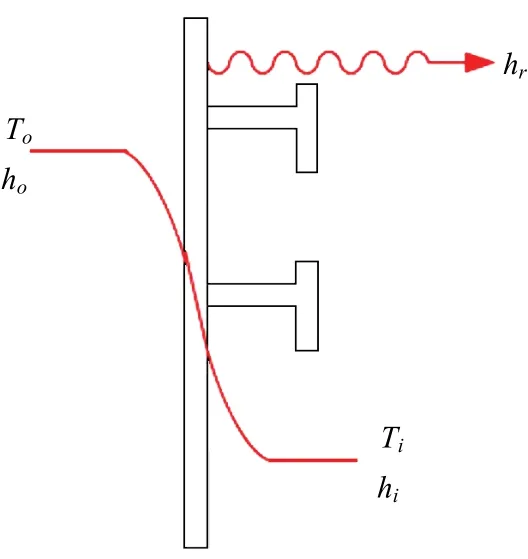
图4 考虑翼翅效应和辐射的对流传热系数

图5 双层板和单层板的温度分布

假如两张不同材料的板叠在一起，两边的温度1T、2T和3T可以计算出来。在平衡状态下穿过各对流边界的热量是相等的。可以得到式(12)：

以矩阵形式表达，即为：

求解该矩阵方程，即可确定板架表面温度。对于单层板来说，三次矩阵方程可以简化为二次矩阵方程，如式(14)所示：

3 温度场计算过程及结果

整个温度分布计算流程如图6所示。

图7为简化的计算模型，将模型分成21块体积，其中7块体积温度为已知（为货物温度、外界空气和海水温度），14块体积温度未知，即有14个方程。

图6 计算流程

图7 计算模型

21块体积能量平衡表示为：

根据IMO及USCG的要求分别进行计算，实际计算表明，吃水对于水线附近的船体结构温度影响较大，特别是根据USCG要求进行的计算。综合IMO、USCG、USCG ALASKA的平浮和横倾各种情况下的计算结果，得出货舱区各构件温度如图8所示。

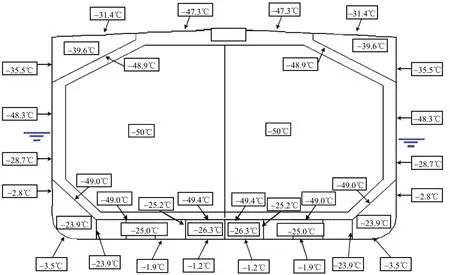
图8 船体结构温度计算结果

4 结 语

VLGC为高附加值船，目前其设计和建造均被日本和韩国垄断[4]。对VLGC的温度场计算进行研究，为船体结构钢材等级的选用[5]提供了依据，为新型VLGC的开发和设计打下了良好的基础。

[1] 国际海事组织（IMO）. 国际散装运输液化气体船舶构造与设备规则[S]. 1993.

[2] 美国海岸警卫队（USCG）. Electronic Code of Federal Regulations (e-CFR)，Title 46： Shipping，PART 154—Safety Standards for Self-propelled Vesseds Carrying Bulk Liquefied Gases[S]. 2004.

[3] 英国劳氏船级社（Lloyd’s Register）. Rules and Regulations for the Construction and Classification of Ships for the Carriage of Liquefied Gased in Bulk[S]. 2010.

[4] 胡可一. 数字化技术在造船业中的应用[J]. 上海造船，2011, (1)： 31-33.

[5] 顾 俊，王凡超. 液化气运输船温度场分布研究及钢材匹配[J]. 船舶与海洋工程，2012, (4)： 1-5.