Chan算法和Taylor级数混合算法的微震源定位方法研究

杨俊峰

（中北大学 电子测量技术国家重点实验室，山西 太原 030051）

1 引言

震源定位是地震学中最基本的问题之一。准确的震源定位对地震活动性分析、震源机制求解以及地球内部探测等都是非常重要的。震源定位除了受地震台网分布、走时拾取精度、速度模型准确性等因素影响外，还与定位算法密切相关。本为利用Chan算法的定位结果作为泰勒级数展开法的初始值进行迭代，从而实现算法优化。仿真结果及数据分析，表明了该算法能有效提高定位精度[4，5]。

2 震源定位原理

对震源进行定位，实质上是一种无源定位技术，采用多站侧向交叉的方法来实现对震源的定位。震源定位系统的每个基站通常由长基线组成，接收基站由4个以上接收传感器阵元按某种几何关系进行布阵。由于各传感器接收信号时无法实现同步，只能利用信号到达N个传感器之间的时延差，建立双曲面交汇模型求解震源位置。

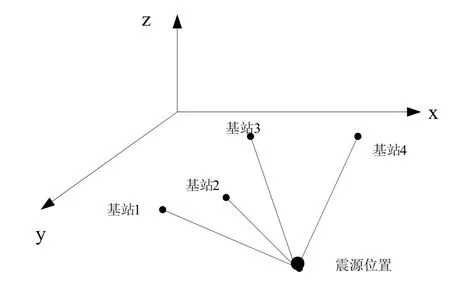
建立三维坐标系，xoy面平行于水平面。Oz轴与xoy平面垂直指向上方。设震源位置坐标为（x，y，z），4 个基站的坐标分别为（xi，yi，zi），（i=0，1，2，3）。震源到基站的距离为ri（i=0，1，2，3）。震源到各分站与主站（基站0为主站）的距离差为ri0。震源定位示意图如图1所示。根据时差定位原理有如下关系：

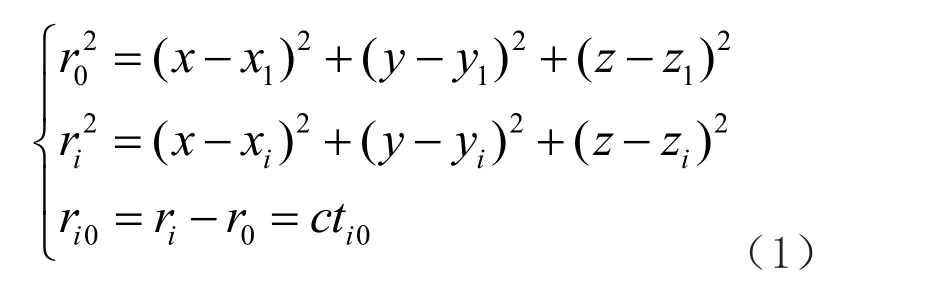
其中，ti0表示震源信号到达分站与主站之间的时间差，c为震动波传播的速度。

3 Chan——泰勒级数展开混合算法

3.1 Chan算法求初始值[2，6]

在多站台的震源定位系统中，选取4个台站的震动波走时方程组，将其线性化得：

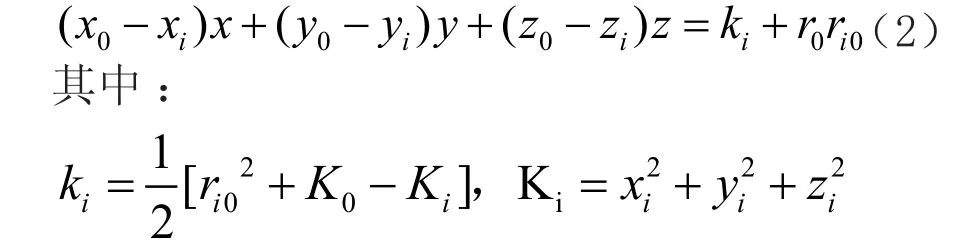
可得到矩阵表达式：AX=F （3）

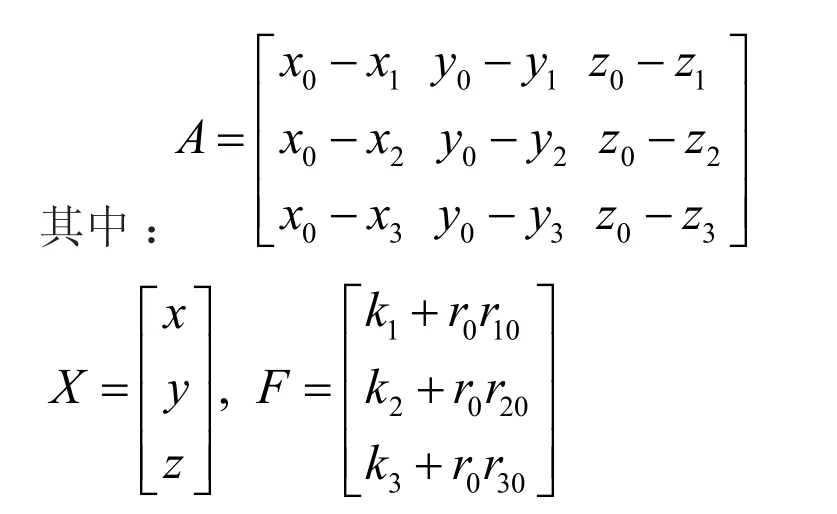
在基站位置布置合适条件下，使rank（A）=3，用伪逆法可求的震源位置估计值：X=（ATA）-1ATF

3.2 泰勒级数展开法定位算法 [1，3，7，8]

泰勒级数展开法是一种递归算法，每一步迭代方向都是沿着当前点函数值下降的方向。因此，初始值的选取对算法的收敛情况至关重要，根据泰勒级数展开法的条件，将所建立震源定位模型转换为：

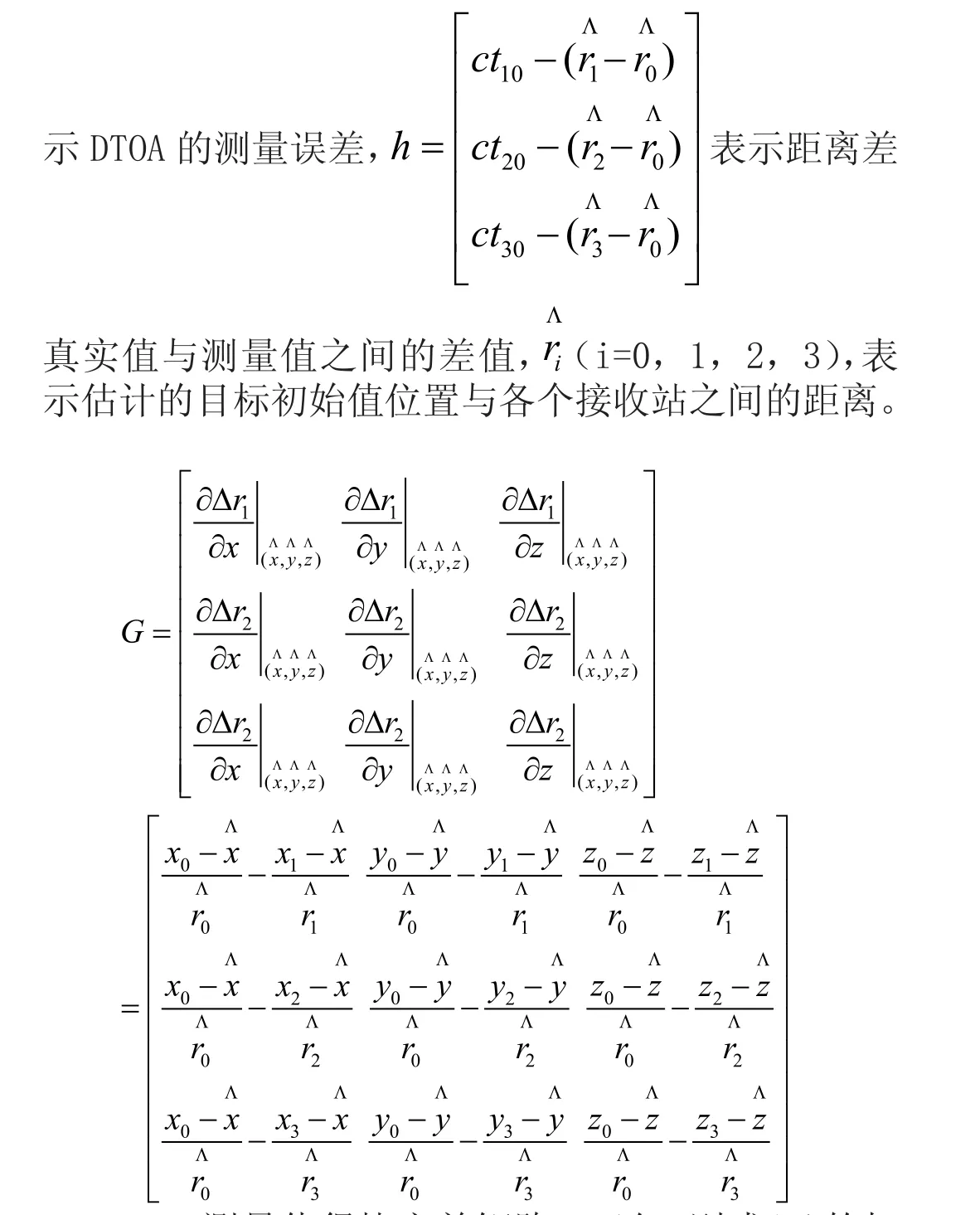
DTOA测量值得协方差矩阵Q已知，则式（4）的加权最小二乘解：

4 震源定位仿真结果分析

在震源定位仿真中，其中主站坐标为（0，0，0），其它 3 个基站坐标为（0，6，-0.3），（-3，10，-0.4），（3，10，-0.5）。在基于传播介质为均匀介质的条件下，设震动波的传播速度为400m/s。在震源周围分别布设上四个加速度传感器，获取传感器基站间的时差。设置六个震源位置，其初始位置为（4，5，-2），（5，7，-3），（6，8，-4），（7，9，-5），（8，10，-6），（9，11，-7），在TDOA测量均方根误差为10us下，分别利用Chan算法、Chan——牛顿迭代混合算法对震源进行仿真定位，实际震源轨迹、Chan算法定位轨迹和混合算法定位轨迹如图2所示。

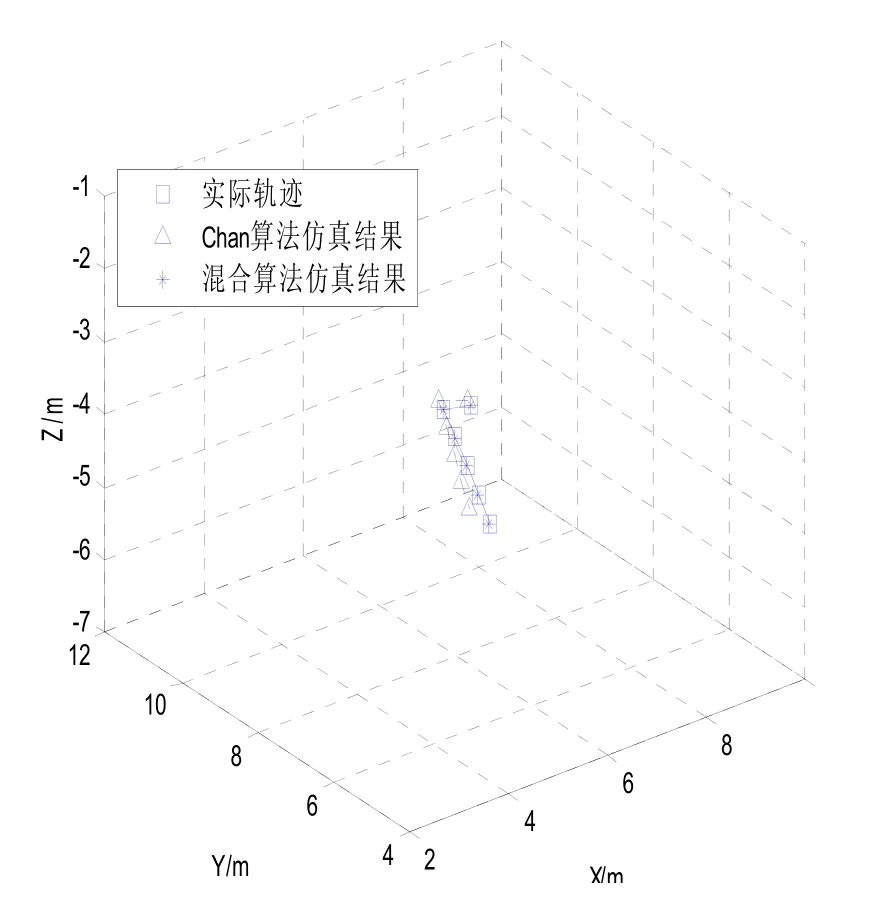
图2 两种算法的震源轨迹仿真

在不同的TDOA测量均方根误差（10us-100us），震源实际位置为（10，10，-10）的情况下，Chan算法、Taylor算法和混合算法的均方根误差（RMSE）的比较，如图3。

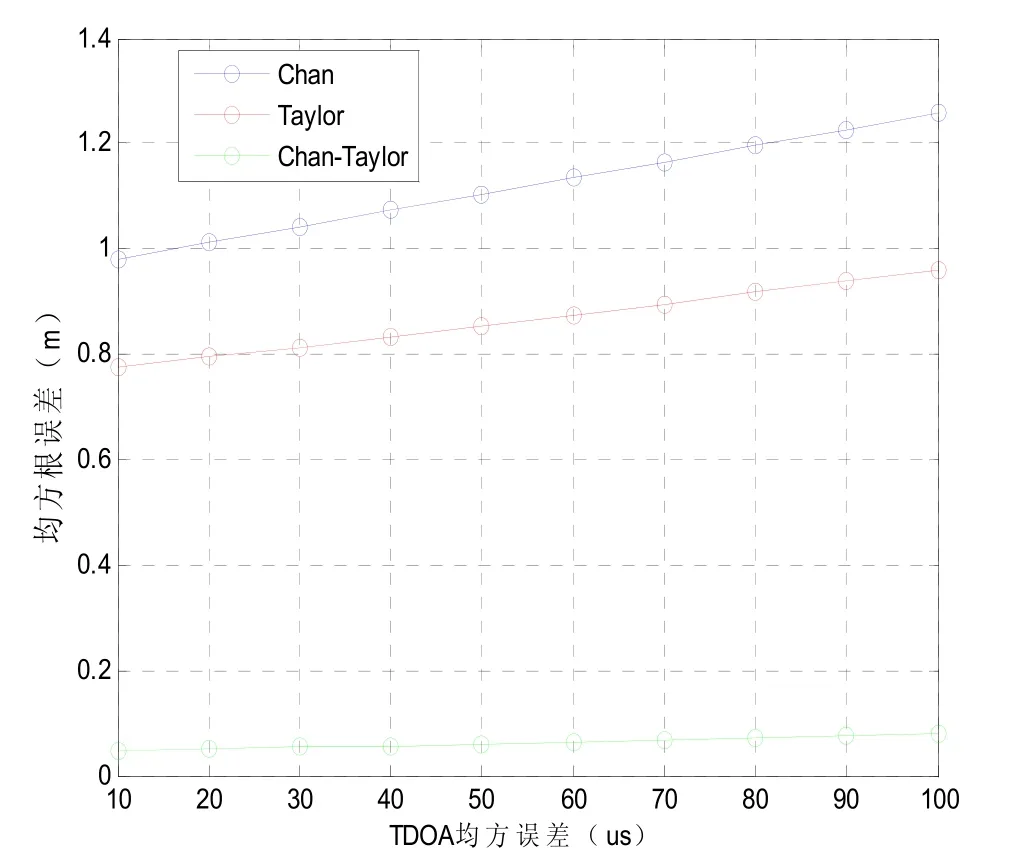
图3 TDOA均方误差对对均方根误差的影响

图2表明Chan算法和混合算法的定位仿真轨迹与震源的实际轨迹的逼近程度。从图中可以看出，混合算法的仿真轨迹更逼近实际轨迹。图3表示了TDOA测量误差对三种算法定位精度的影响。从仿真曲线的变化过程可以看出，随着TDOA均方误差的增大，三种算法的均方根误差也逐渐增大。在各种误差均方根的情况下，混合算法的定位精度要明显高于Chan算法与Taylor算法，并且混合算法的定位位差随着TDOA测量误差上升的速度比Chan算法和Taylor算法 要慢。结合以上仿真结果可以看出，TDOA测量误差对混合算法的定位精度的影响要小于Chan算法和Taylor算法，说明本算法能有效抑制由于测量误差而带来的均方根误差。

5 结束语

由仿真和分析可知，本文提出的Chan算法与泰勒级数混合算法具有良好的收敛性能，定位精度高，有效地抑制了由于测量误差而带来的均方根误差，在测量误差复杂的情况下要优于Chan算法和Taylor级数算法，具有一定的可用性。

[1] 李莉，邓平，刘林.Taylor 级数展开法定位及其性能分析[J].西南交通大学学报.2002（6）：684-688.

[2] Chan T Y，Ho C K.A Simple and Estimator for Hyperbolic Location[J].IEEE Trans.On Signal Processing，1994，42（8）：1905-1915.

[3] 熊瑾煜，王巍，朱中梁.基于泰勒级数展开的蜂窝TDOA定位算法[J].通信学报.2004（4）：144-150.

[4] 田玥，陈晓非.地震定位研究综述[J].地球物理学进展 .2002，17（1）：147-155.

[5] 杨文东，金星，李山有.地震定位研究及应用综述[J].地震工程与工程振动.2005，25（1）：14-20.

[6] D.J.Torrieri.Statistical theory of passive location systems.IEEE Transactions on Aerospace and Electronic Systems，1984，20（2）：183-198.

[7] 张令文，谈振辉.基于泰勒级数展开的蜂窝TDOA定位新算法[J].通信学报.2007，28（6）：7-11.

[8] 史有华，谢红，杨莘元.WCDMA 网络中基于泰勒级数展开的 TDOA 定位技术研究[J].应用科技.2006（1）：1-3.