超声波多普勒流量计性能的改进研究

梁 璐 高国旺 殷 光 孙亮亮 范祥辉

（1.西安石油大学光电油气测井与检测教育部重点实验室，陕西 西安 710065）

0 引言

超声波流量计是一种非接触式流量计量仪表，它被广泛的应用在石油、化工及日常生活中的方方面面。在超声波流量计中多普勒法是其中的重要一种，它适用于测量混合介质流体流量。超声波多普勒流量计通常由超声波传感器，超声波发射和接收装置以及信号处理系统三部分组成。其中，信号处理系统是对接收到的微弱信号进行一系列模拟和数字方式的处理，从而分析出测量管段中流体的流量。目前，市场上的超声波多普勒流量计产品很多，它们对于多普勒频移信号的处理大多数都是采用模拟滤波、频率转电压、整形计数或者是简单的傅里叶变换（FFT）等方式。因此，它们普遍存在着测量稳定性差、精度低、动态响应慢等问题，尤其是在低流速管道流量测量时，测量结果偏差较大，甚至没有参考性。

针对超声波流量计存在的上述问题，本文从硬件电路和信号处理方法两方面进行了研究。在硬件上对微弱的多普勒回波信号进行了多级放大、滤波、解调等处理，从而将回波信号调整在10kHz的频带上，提高了系统对于流量变化的响应速度。文中使用数字信号处理器（DSP）对调理后的多普勒频移信号进行模数转换，将得到的数字序列进行复调制频谱细化（ZOOM-FFT）运算及相应的数字滤波，提高了多普勒频移信号的频谱分辨率，从而提高了流量的分辨率。

1 超声波多普勒流量测量原理

声学中，当声源与观察者相对于媒质运动，或两者同时相对于媒质运动时，观察者接收到的频率与声源发出的频率不同。当声源与观察者之间的距离随时间缩短时接收到的频率高于声源发出的频率；反之，接收到的频率低于声源频率。声源发出的频率与观察者听到的频率之间的频率差称为多普勒频移，它的大小取决于两者之间的相对运动速度，这种现象称为多普勒效应[5]。

在利用超声波多普勒法测量时，超声波传感器的激励方式主要有两种分别为：单载频脉冲波激励，连续正弦波激励[6]。本文中采用连续正弦波信号激励方式，用一对斜探头垂直对称安装在管道外侧（如图1所示），发射探头产生的连续波超声信号经声楔和管壁进入运动中的流体，并被随流体一起运动的固体悬浮颗粒、气泡等可以散射超声波信号的物质散射而进入接收探头。通过测定流体中运动粒子散射声波的多普勒频移，完成流量检测。

超声波多普勒流量测量示意图如图1所示，超声波在被测流体中的传播速度为c，u为悬浮颗粒在流体中的流速，β为超声波束在管壁中的入射角，α为声楔的角度，f1为超声波的发射频率，f2为接受的超声波信号的频率，fΔ为多普勒频移，其中θ为超声波在流体中的传播方向角度。

图1 多普勒流量测量示意图

其中多普勒频移与流速之间的关系如式（1）所示

2 多普勒流量计硬件系统设计

多普勒流量计硬件系统主要是完成对超声波信号的发射、接收和相关处理，以及对流量计外部设备的控制等，系统框图如图2所示。本文采用一对中心频率在640kHz的超声换能器分别作为发射和接收探头，利用频率为640kHz的连续正弦波驱动超声发射电路使其在管道中发射超声波。接收端采用选频放大电路接收超声回波信号，再经过解调电路将多普勒频移信号解调到中频10kHZ上。DSP芯片对解调后的信号进行A/D转换，然后利用选带频谱细化ZOOMFFT算法精确的获取到多普勒频率偏移量。在进入A/D之前必须经过抗混叠滤波以避免在模拟输入信号上叠加周期或者非周期的干扰信号，从而附加到量化值中，给有用信号带来一定的干扰。本文中的DSP芯片选用的是TI公司的TMS320x2812，它不仅完成了上述任务，还对系统的液晶显示、数据存储、数据通信等进行了控制。

图2 系统硬件框图

本文设计中发射及解调的基准信号都是通过DDS芯片产生的，它可以稳定地输出单一频率的正弦波和方波波形，从而降低了由于发射信号及解调参考信号频率抖动对于多普勒频移信号的影响。由于DDS产生的640kHz正弦波幅度较小、功率较低，而管道和流体会对超声信号进行衰减，所以要将DDS产生的正弦波通过超声波信号发射电路进行一定程度的幅度和功率放大。超声波信号发射电路还有一项重要工作就是与超声换能器电学匹配，只有在匹配情况下换能器才能最大效率的向流体中发射超声波。

由于换能器的发射信号在经过传感器和管道、介质等的衰减之后，到达接收端是一个微弱信号，而此微弱信号中包含着流体流动的信息，所以回波接收电路的好坏对于流量计的性能有着重要的影响。本文所设计的回波信号接收电路包括两部分，选频放大电路和低噪声前置放大电路。选频放大电路对接收探头接收的微弱信号进行一定程度的频率选择和放大，滤除发射频率一定范围外的噪声，并且在不超过解调电路允许的电压范围内提高信号的幅度，以利于后期信号处理。低噪声前置放大电路对接收到的超声回波信号进行二次放大，同时将接收到的信号转换成差分信号输出，以满足解调电路对信号幅度等的要求。

在采用频谱分析技术计算多普勒频移时，如果直接对接收到的高频信号进行频谱分析会存在两方面的问题：（1）需要较高的采样率；（2）频率分辨率在高采样率的情况下，要获得较高的频率分辨率需要采样点数足够大，对存储空间的要求较高且计算量大[7]。所以本设计将回波信号先进行解调，然后再进行频谱分析。对于信号解调，通常都是将信号解调到直流0Hz上，但这样易受电源及其他低频噪声的干扰，使频谱分析出来的结果不能准确表征管道内的流体流动。将信号解调到0Hz上还有一个问题，那就是在低流速情况下，要准确分析出多普勒频移量就要延长信号采集时间，从而降低了系统的动态响应。因此，本设计采用了外差法进行解调，它是通过将回波信号与一个非载波频率信号（设计中采用2.52MHz的方波信号，经过解调芯片内部的4分频后为630kHz）进行相干解调，将信号解调到10kHz，从而将多普勒频移解调在差频信号上，这样就得到了一个包含流体流动的流速信息和方向信息的低频信号。

解调后的信号需要经过调理后才能进入DSP的ADC模块。信号调理主要是对解调芯片的输出信号进行电流电压转换、低通滤波以及信号抬升，以满足后续信号处理的要求。

3 多普勒频移信号处理方法

在超声波多普勒流量测量技术中，多普勒频移信号处理方法直接影响着测量系统的性能。现有多普勒流量计产品中，对于频移信号的处理方法大致分为整形计数、频率转电压和频谱分析三类，总体来说，前两种方法在系统稳定性、测量准确度等方面都不如频谱分析法。频谱分析能够揭示多普勒频移信号

方法（ZOOM-FFT）对多普勒频移信号进行处理，它是一种更为有效的动态信号分析方法，ZOOM-FFT法不管从分辨率、计算量、实时性等方面都明显优于传统傅里叶频谱分析法。

3.1 ZOOM-FFT频谱细化算法

复调制ZOOM-FFT 算法能以指定的、足够高的采样频率分析任意频段内信号的频谱结构。在序列变换点数相同的情况下，ZOOM-FFT能获得更高的频率分辨率，在相同的频率分辨率下，它比基带FFT需要更少的傅立叶变换点数，因此ZOOM-FFT非常适用于要求大频率分析范围、高频率分辨率和少变换点数的场合。

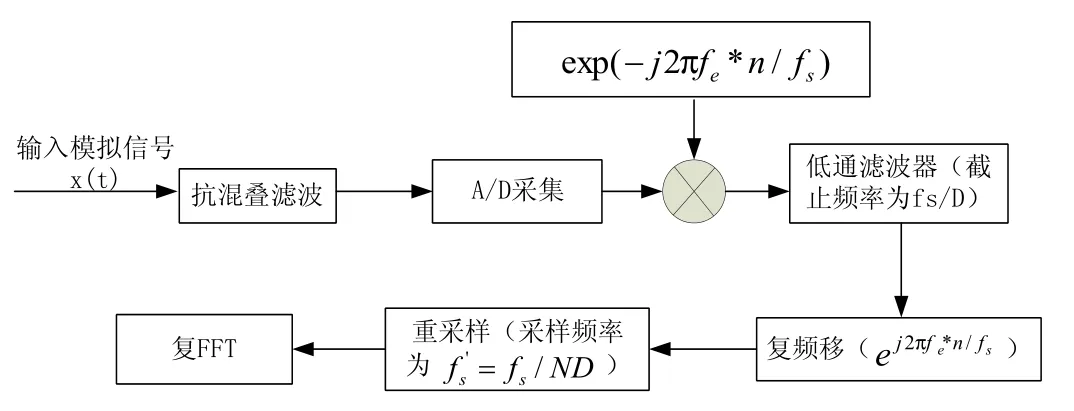
图3 ZFFT原理流程图

模拟信号x（t），经过抗混叠滤波之后进行A/D采集得到时间采样序列x（n），fs为采样频率，fe为需要细化的中心频率，细化倍数为D。复解析带通滤波器的带通宽度为 隔D点选抽一点，移频和做N点谱分析，频带（f1～f2）用N条独立谱线表示。具体算法的实现步骤如下：

（1）复调制移频；所谓复调制移频就是对原始信号的频域进行向左或向右的搬移，根据离散傅立叶变换的频移性质，x0(n)为A/D采集后的离散信号，

（5）复FFT；假设原始信号谱线为N条，对重采样后的信号进行复FFT，经过重采样后谱线数为N/D，分

3.2 算法的仿真与验证

对于本系统中解调后得到的10kHz中频上的信号，选择中心频率为10KHZ，采样频率为50KHZ，进行4096点的FFT和ZFFT算法进行仿真比较。图4表示直接进行4096点的FFT频谱图；图5为进行细化倍数D=4，fft点数为4096的细化后的频谱。

图4 4096点的FFT

图5 ZOOM-FFT（细化倍数D=4）

由于频偏成分与中心频率之间的频率间隔为100HZ，通过图5可看出，直接进行FFT显然很难分辨出中心频率和频率偏移，它的频谱分辨率为fs/整数倍）来改变频谱分辨率，细化4倍后频谱分辨率可达到3HZ，通过对比可得出，ZOOM-FFT算法不但频谱分辨率得到了提高，而且算法的稳定性好，能够有效的提高信号检测的准确性。在超声多普勒流量计的研制中，局部频谱细化的应用有利于后期谱峰搜索范围的减小及计算流速的精确性。

4 结束语

在研究了超声波多普勒流量测量理论的基础上，针对目前多普勒流量计存在的稳定性差、灵敏度低、测量误差大等问题，本文从硬件电路设计和信号处理方法两方面改进了多普勒流量计的性能。主要的改进包括：

（1）采用先进的DDS芯片产生超声发射电路及解调电路中的基准信号。DDS芯片输出具有高精度、高稳定度的特点，它可以很好的解决由于温度等变化引起的基准信号抖动，降低了基准信号变化对于多普勒频移信号的影响。

（2）中频解调技术。通过解调芯片将多普勒频移信号解调在10kHz的频带上，提高了在频谱分析点数一定的情况时系统的灵敏度。

（3）在DSP芯片中使用复调制频谱细化算法（ZOOM-FFT）对多普勒频移信号进行频谱分析。ZOOMFFT算法有效地提高多普勒频移信号的频率分辨率，并减小了DSP的计算量，解决了多普勒流量测量系统的测量精确度及低流速情况下的测量准确性。

[1] 江波.唐普英.基于复调制的ZOOM-FFT算法在局部频谱细化中的研究与实现.[J].大众科技 .2010.131（7）.48-49.

[2] 李朝晖.刘连傅.姜天仕.段慧明.翟秀贞.流量测量中超声多普勒信号的频谱特点及其与管道中流速的关系.[J].计量学报.1995.16（1）.68-72.

[3] 丁丽晶.基于DSP技术的超声波多普勒流量计的设计.[D].大连理工大学.2002.

[4] 罗守南.刘岩.冯冠平.连续波超声多普勒管道流量测量.[J].仪表技术与传感器.2004.12.44-46.

[5] 冯若.超声手册[M].南京.南京大学出版社.1999.[6] 张俊哲.无损检测技术及其应用（第二版）[M].北京.科学出版社，2010.

[7] 罗守南.基于超声多普勒方法的管道流量测量研究.[D].清华大学.2004.

[8]丁康.谢明.杨志坚.离散频谱分析校正理论与技术.[M].北京.科技出版社.2008.