LCL滤波并网逆变器的零点配置策略

许津铭，谢少军，肖华锋，黄如海，秦 岭

(1.南京航空航天大学自动化学院，江苏 南京210016;2.南通大学，江苏 南通226007)

引言

并网系统中，采用LCL滤波器可以较好的滤除进网电流中的高次谐波电流，但高阶滤波器的存在降低了系统阻尼，并网电流甚至产生无阻尼谐振，危及并网逆变器的安全及稳定运行。为此，多数文献中采用无源阻尼或者有源阻尼的控制方案。无源阻尼方案中，通过在滤波器中串联或并联电阻实现系统阻尼特性的改善[1,2]，但该方案所带来的损耗问题制约了其应用。而有源阻尼方案则是通过控制算法给系统引入虚拟阻抗，改善阻尼特性，这种方式不会带来多余的损耗。

已见诸文献的有源阻尼方案，包括逆变器侧电感电流[3]、电容电流[4～6]、电容电压[6,7]、网侧电感电压[8]的单变量反馈的有源阻尼方案，以及采用多变量组合的有源阻尼方案等[9]。综观上述文献，由于控制系统的阶数较高，调节器参数的设计较为复杂。除此之外，文献[10]中给出了一种新型的控制思想：按照一定比例分裂滤波电容，对两电容之间的电流进行闭环控制，实现了控制环路上的降阶，为系统闭环设计带来方便，控制器的设计不存在上述方案的问题。但该方案需对硬件电路进行改动。文献[11]通过对逆变器侧电流与网侧电流的加权平均获得了具有一阶特性的电流量，同样实现了降阶控制，实现较为简便。

文献[11]中的方案仅仅是针对单一方案进行分析，并未全面的分析各电压以及电流之间的可能的组合方式。本文提出了一种系统性的分析方法，从零点配置角度全面讨论了LCL滤波并网逆变器系统中的加权组合方案，给出了在LCL滤波并网系统中可行的组合反馈方式。仿真以及实验结果验证了分析的有效性。

1 电流加权的控制方案

图1(a)所示为采用LCL滤波器的单相并网逆变器，由逆变器侧电感L1、滤波电容C1及网侧电感L2组成。逆变输出至进网电流的幅频特性见图1(b)，进网电流中存在谐振尖峰，不利于闭环设计。尤其是，采用进网电流直接闭环控制时，需要将谐振峰抑制到0 dB以下保证系统稳定[3]。这意味着较差的系统响应。

文献[11]中采用的电流加权方案如图2所示。为简化分析，将全桥逆变环节等效为比例增益，忽略其延迟的影响。当加权系数β=L1/(L1+L2)时，即可得到一阶特性的加权组合电流量，如式(1)。该方案实现了反馈控制系统的降阶，闭环设计较为简便。具体的设计以及系统参数扰动下的鲁棒性详见文献[11]。

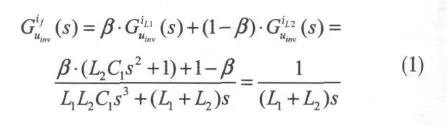
2 零点配置的系统性分析

由式(1)可以看出，该方案的实质是通过合理选取加权组合系数实现了组合量中零点的配置，配置零点与谐振极点抵消。为全面研究可行的加权组合方式，本文给出基于零点配置策略的统一控制框图(图3)，其中x1与x2为三个滤波元件的六个电流电压量，本文将加权形式扩充到比例、积分、微分的加权组合，即 xf=f(x1,x2)=k1sm·x1+k2sn·x2，m,n∈{0,±1}。 选取的加权组合需实现如式(1)所示分母为一阶的传递函数，将高阶的系统等效为单电感滤波的一阶并网系统，简化了系统控制。

从分析结果来看(表1)，以实现抵消谐振极点为目的的零点配置方案比较多，主要可分为两个电流的加权组合、两个电压的加权组合以及电流与电压的加权组合。从表中还可以看出，电流之间的加权组合方式最为简单，权值均为比例系数。而其它两大类的权值均有涉及到积分或者微分形式。总结来看，这两类的组合方式均同电流加权组合相似，可依据各元件电流电压间的关系相互导出。需要注意的是，若实现了电网电压的解耦，滤波电容电压同网侧电感电压一致。

表1 零点配置的组合方案

表中第一个电流组合方式即为文献[11]中采用的控制方案。对于表中所示的多种组合方案来说，其原理是基本一致的，但所需采用的传感器却大不相同。而对于不同的并网系统、不同功率等级或者电压等级下，选择不同的传感器的成本可能是不一样的[6]。因而有必要对其它可行的组合方案进行研究。

3 电流间组合方案的实验研究

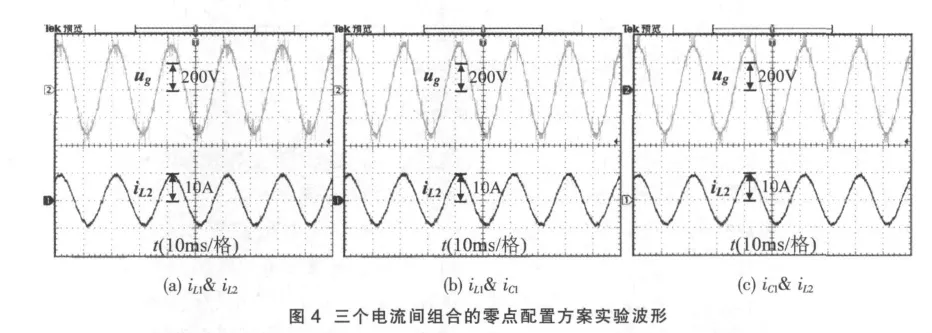
文献[11]中对电流组合方式中的第一种进行了详细的实验研究。需要指出的是，电容电流的幅值相较于其它两个电流要小，同时三个电流在系统中位置也不一样，不同的选择可能会带来成本上的降低。本节对LCL滤波器中易于测量的三个电流间的三种加权组合方式进行实验研究，闭环采用简单的PI调节。搭建了一台单相并网逆变器，滤波器参数为：逆变器侧电感值1 066 μH、网侧电感值1 022 μH、滤波电容值10 μF。实验条件为：直流输入电压360 V，电网电压 220 V/50 Hz，开关频率 10 kHz。图4中分别给出了三种组合方式下的并网实验波形。从实验结果可以看出，进网电流波形正弦度好，这三种零点配置组合方案均是有效的。应用中，设计人员可以自由的选择电流传感器的位置。

4 电压间、电流电压间组合方案的仿真研究

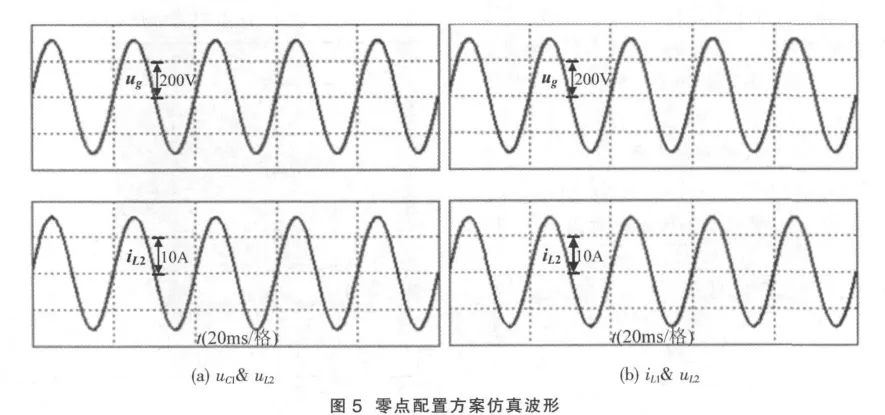
前文对三个电流间的两两加权组合方案进行了实验研究。本节采用saber仿真软件针对三个电压间的以及电流电压间的组合方案进行仿真研究，仿真参数同第3节所示。表1中示出的组合方案较多，本节分别从电压组合方案以及电流电压组合方案中各选取一种方案进行仿真验证，即：图 5 分别给出了两种组合方案下的并网仿真结果，方案是可行的，可以进一步扩宽该类方案的应用。

5 结论

本文采用了一种系统性分析方法研究了LCL滤波并网逆变器的零点配置的电流控制技术，给出了可实现对消谐振极点的变量组合方案。对三个电流间的两两组合方案的实验以及电压间、电流电压间的组合方案的仿真均表明分析的正确性，可以拓宽该类方案实际应用中传感器选择的范围。

[1]Wenqiang Zhao,Guozhu Chen.Comparison of Active and Passive Damping Methods for Application in High Power Active Power Filter with LCL-filter[C].Sustainable Power Generation and Supply,2009.

[2]M Liserre，Blaabjerg F，Hansen S.Design and control of an LCL-filter based active rectifier[J]．IEEE Trans.on Industry Applications,2005,41(2):1281-1291．

[3]R Teodorescu，F Blaabjerg，U Borup，et al．A new control structure for grid-connected LCL PV inverters with zero steady-state error and selective harmonic compensation[C]．APSC，2004，Nineteenth Annual IEEE Vol.1，2004 Page(s):580-581．

[4]徐志英，许爱国，谢少军．采用LCL滤波器的并网逆变器双闭环入网电流控制技术 [J]．中国电机工程学报，2009，29(27)：36-41．

[5]刘飞，段善旭，查晓明．基于LCL滤波器的并网逆变器双环控制设计 [J]．中国电机工程学报，2009，29(S1)：234-240．

[6]J Dannehl,F W Fuchs,S Hansen,and P B Thogersen.Investigation of active damping approaches for PI-based current control of grid-connected PWM converters with LCL filters[C].IEEE ECCE 2009:2998～3005.

[7]M Malinowski，S Bernet．A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL Filter[J]．IEEE Trans.on Industry Electronics，2008，55(4)：1876-1880．

[8]王学华，阮新波，刘尚伟．抑制电网背景谐波影响的并网逆变器控制策略[J]．中国电机工程学报，2011，31(6)：7-14．

[9]J Dannehl，F W Fuchs，S Hansen，et al．PI state space current control of grid-connected PWM converters with LCL filters[J]．IEEE Trans.on Power Electronics，2010，25(9)：2320-2330．

[10]沈国桥，徐德鸿.LCL滤波并网逆变器的分裂电容法电流控制[J].中国电机工程学报,2008,28(18):36-41.

[11]Guoqiao Shen，Xuancai Zhu，Jun Zhang，et al．A new feedback method for PR current control of LCL-filterbased grid-connected inverter[J]．IEEE Trans.on Industrial Electronics，2010，57(6)：2033-2041．