打点计时器测加速度——你错了吗

◆简增珂

打点计时器分为电磁打点计时器和电火花打点计时器，是学生进入高中学习阶段在物理学科所接触的第一个测量工具。用打点计时器测加速度是高中物理的一个重要实验，对培养学生科学的认知态度、良好的动手实验操作能力、严谨的数学运算能力以及合作学习等方面意义重大。无论是在历年高考中，还是在各地市模拟或检测中，它都占有重要的一席之地。然而，笔者综观当前的教学思路和题目设计的方法，却发现一个问题，那就是错误地把“加速度的平均值”当作“加速度”，错误地把“一次测量”当作“多次测量”，从而错误地用“多次测量求平均值”的方法计算实验小车的加速度。

以下是笔者对这个问题的分析。

1 传统的实验方法

1.1 实验目的

1）练习使用打点计时器；2）测平均速度；3）测瞬时速度；4）测小车运动的加速度。

1.2 实验原理

瞬时速度：对于匀变速直线运动，平均速度等于中间时刻的瞬时速度，。

加速度：在匀变速直线运动中，速度的变化量和所用时间的比值，（定义法）；(逐差法)。在v-t图像中，图线的斜率表示加速度。

1.3 实验器材

打点计时器（电磁打点计时器或电火花打点计时器）、纸带、实验用小车、一端固定有定滑轮的长木板、钩码、细线、电源（学生电源或生活用电）、导线、刻度尺。

1.4 实验步骤

在小车的后面固定一条纸带，打点计时器固定在长木板没有滑轮的一侧，纸带穿过打点计时器的限位孔，用钩码拉动小车在长木板上做加速运动，打点计时器就会在纸带上打出一系列点，这些点就记录了小车的运动情况。换上新纸带，重复操作几次。

1.5 数据处理

从多条纸带当中选择一条用来分析小车的运动，先判断小车是否做匀变速直线运动，然后计算小车的加速度。

1）判断小车是否做匀变速直线运动。如图1所示，把纸带按计数点分段做标记，可采用分段求加速度的方法进行比较。如果用加速度的定义式计算加速度，需要首先计算瞬时速度，这种方法不仅需要进行测量，还要进行多次运算，相对比较麻烦。另一种方法是采用逐项差值法。先测量各计数点之间的距离x1、x2、x3、x4、x5、x6、x7、x8，然后 算 出 差 值：Δx1=x2-x1，Δx2=x3-x2，Δx3=x4-x3，Δx4=x5-x4，Δx5=x6-x5，Δx6=x7-x6，Δx7=x8-x7。如果各差值在误差允许的范围内相等，就可以判断小车做匀变速直线运动。

图1

2）计算小车的加速度。针对所选出的一条纸带，人们往往从减小误差和充分利用测量数据的角度去计算加速度，因此，在差值判断的基础上大多采用逐差法或图像法。

关于逐差法，各类期刊、报纸、教辅资料争议颇多，由逐项逐差法又派生出多项间隔逐差法或者更复杂的逐差法。

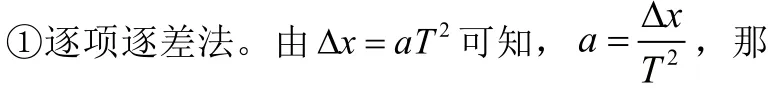
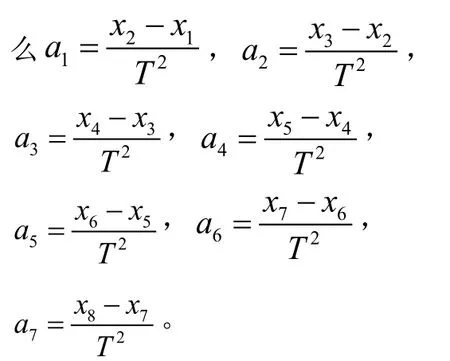
为了减小偶然误差，对所求出的多个加速度求平均值，则：

同样，为了减小偶然误差，对所求的多个加速度求平均值，则：。

③图像法。首先把各时段求出的每一段的平均速度作为中间时刻的瞬时速度：。然后在v-t图像中进行描点。最后用一条直线进行“拟合”，使各点均匀分布在直线上或者分布在直线的两侧，计算直线的斜率求加速度。

从理论上来看，笔者认为以上三种求加速度的方法都是错误的。

2 传统实验存在的错误

传统实验的方法错在哪儿呢？这要从加速度的定义说起。加速度是描述物体速度变化快慢的物理量，是物体速度的变化量与所用时间的比值。也就是说，加速度是对应某一个特定时间段而言的，当时间趋于无穷小时就是瞬时加速度。一般情况下所说的加速度，是指平均加速度。在理想的匀变速运动中，瞬时加速度与整个运动过程的加速度是一致的。

图2

在本实验中，无论是用各段的差值求加速度，还是用各段初末瞬时速度作图求加速度，由于偶然误差的原因，各段所求的数值可能存在差异。这时，人们自然会想到用多次测量求平均值的方法来减小偶然误差。问题就出现在这儿。

首先，从加速度的物理意义可以知道，“加速度的平均值”不等同于“平均加速度”。对于某一个运动过程，可以分不同的时间段求加速度a1、a2、a3…an，但是每一个加速度只对相应的时间段有物理意义。也就是说，加速度与时间段是一一对应的关系。对一个运动过程而言，不同时段“加速度的平均值”只是一个数学问题，只能表示不同几次分别求密度就叫做多次测量；因为每一次的测量会存在误差，所以通过多次测量求平均值可以减小偶然误差，该平均值就是这根胡萝卜实验测量的密度。但是，如果把一根胡萝卜等长度切成几段，测每一段的质量和体积计算密度，就属于不同的测量，每一段胡萝卜密度的不同可以称之为“差异”而不能称之为“误差”。

所谓“多次测量”，意味着针对同一个需要测量的物理量重复实验操作。打点计时器是一种特殊的测量工具，能同时记录运动物体的“时间—空间”信息，每打一条纸带只对应一次实验操作，是对物体运动的一次测量。一个过程中的不同时段会存在“差异”而不是存在“误差”。

从另一方面，应该全面综合考虑运动过程中出现的各种偶然因素，用发展的眼光看待这些偶然因素产生的影响，不能片面地认为这一段的误差偏大而那一段的误差偏小。

下面，笔者从整体的角度来分析小车的运动。

小车在整个运动过程中不可避免地会出现这样或者那样的偶然因素，而小车最终的运动状态就是包含这些偶然因素的必然结果。从混沌学的角度来看，一个偶然因素产生的影响会持续到事件发展的结尾，也就是说，后面的偶然因素包含前面的偶然因素产生的影响，整个运动过程是“鸡生蛋，蛋生鸡……”的一个有机的整体。在小车的运动过程中，某一个偶然因素产生了影响，则小车的运动因此会发生一些变化，不管是经过多长时间，小车的运动都是在这个变化的前提下进行的；反之，这个偶然因素显然也是因为之前的其他的偶然因素产生的变化所造成的。所以，小车时间段的加速度大小上存在差异，有的比平均值大，有的比平均值小。对整个运动过程而言，只有它的数学意义而没有实际的物理意义。

图3

为了方便理解，先以速度这个物理量举例：一只小蚂蚁从一根细竹竿一端爬到另一端，已知小蚂蚁爬过每一节竹竿所用的时间，求小蚂蚁爬行的速度。从速度的定义可知，用小蚂蚁通过的总位移和所用总时间的比值就可以求出这个速度。那么，能不能先对小蚂蚁爬过每一节竹竿求速度，再用取平均值的方法求小蚂蚁的速度呢？当然不能。同理，用不同时段的几个加速度求平均，显然不能等效替代整个运动过程的加速度。

其次，这些加速度是“多次测量”的数据吗？不是。这些加速度只是对小车加速度一次测量中的分时段求值而已，应该属于不同的测量。再举个简单的例子：测一根胡萝卜的密度，每测一组质量和体积就能计算一次密度，多测最终的运动状态本身就是一个个误差累积作用的结果，已经不能孤立地看待整个运动过程中某一段运动的误差。既然整个过程中的各种误差本身已经累积作用，再试图通过分段取平均来减小误差，显然是毫无道理可言的。

“开弓没有回头箭”，可以分段分析“一支箭”在不同时段运动的差异，但绝不能用某一段的运动代替“一支箭”运动的“全部”。

3 正确的实验思路

正确地用打点计时器测加速度的实验操作步骤和传统实验是相同的，只是在计算加速度的数据处理上有所不同。

3.1 若只用一条纸带测加速度

由前面的分析可知，如果只用一条纸带，则只是对小车的加速度进行了一次测量，只能整体计算出一个加速度。可以选用纸带两个远端各取两个计数点求加速度，这个加速度就是小车实际物理意义上的加速度。

2）用间隔差值法求加速度：

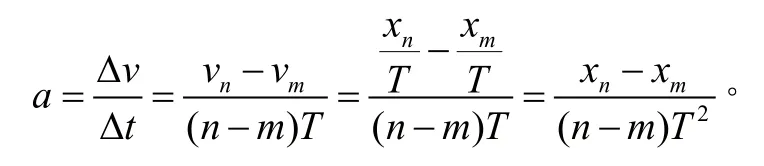
由以上推导可知，间隔差值法实质上也是定义法。对比以上两种方法可以看出，如果选用定义法，实验中所直接测量的数据先参与商值运算求瞬时速度，再参与差值运算求速度的变化量，最后参与商值运算求加速度，由于保留位数和有效数字的原因，误差会不断增大。如果选用间隔差值法，所测数据先参与差值运算求位移差，再参与商值运算求加速度。因此，从减小计算所产生的误差来说，推荐使用间隔差值法。

3.2 若用多条纸带测加速度

如果用打点计时器进行多次实验操作，选择多条纸带，则每条纸带可以分别求一个加速度，最后求和取平均值：。

总之，应该全面地看待事物发展的规律，科学地认识加速度的物理实质，充分理解打点计时器这一测量工具的测量原理，只有这样才能真正体现本实验的意义和价值。