西江水文干旱历时与强度的遭遇概率分析*1

陈子燊，刘占明，黄 强

(中山大学地理学院水资源与环境系，广州510275)

进入21世纪以来，全球气候变化背景下的区域干旱现象非常引人注目.由于干旱的发生与发展过程具有渐进性和持续性、影响范围广等特征，如形成灾害将对区域经济社会发展造成重大影响.从概率的角度分析并预测干旱发生的规律，可为区域水资源规划、风险管理、防旱抗旱与制定区域社会与经济发展规划或计划等提供决策依据.干旱类型通常可分为气象干旱或气候干旱、农业干旱、水文干旱及社会经济干旱4类［1］.其中，水文干旱被认为是气象干旱和农业干旱的延续和发展，是最终最彻底的干旱［2］.

目前，国内外应用游程理论和Copula理论与方法在量化干旱特征与变化规律的研究方面做了不少研究工作.其中，Fleig等［3］采用3种方法:滑动平均方法(MA-procedure)、事件间隔方法(IT-method)和连续峰值算法(SPA)对径流干旱特征值的提取做了综合评价.周玉良等［4］以径流量为水文干旱指标，通过径流量距平百分率和径流量累积频率两种方法识别水文干旱特征变量，并以适线法确定单个干旱特征变量的分布曲线，在此基础上利用Copula函数构建了干旱历时与干旱烈度间的联合分布.陆桂华等［5-10］分别利用游程理论提取降水资料或标准降水指数(SPI)的干旱特征值，应用Copula方法计算干旱历时和干旱烈度的联合分布概率，推算干旱极限事件重现水平.尹正杰等［11-14］分别利用截断水平提取水文干旱事件，应用马尔可夫平稳概率和一阶自回归模式模拟随机合成的径流，研究干旱强度、干旱烈度、干旱历时和强度及风险概率等统计特征.不过，由于干旱烈度至今尚没有一个明确的指标划分标准，而干旱强度指标是建立在概率分布基础并可直接联系旱情级别，建立干旱历时和干旱强度之间的联合分布将可直接分析干旱风险及给予概率意义上的预测.

1 水文干旱频率分析方法

1.1 水文干旱指标

对水文干旱指标划分的研究表明［15］，Seiler等［16］提出的标准化降水指标(SPI)优于在我国广泛应用的Z指数.Nalbantis等［17］采用了与SPI相同的方法计算水文年多时间尺度的径流干旱指数(Streamflow Drought Index，SDI).首先采用伽马分布描述不同时间尺度的月径流量的偏态分布，进而经标准正态化得出SDI.由此计算获得的SDI不仅可量化描述多时间尺度的水文干旱特征，而且适用于不同时间与空间尺度的干旱监测和评价.具体计算方法如下:

假设某一时间尺度下的径流量为x，则其满足伽马分布的概率密度函数f(x)为:

式中，α、β分别为形状参数和尺度参数.给定时间尺度的径流量x的累积概率为

对Γ分布概率进行正态标准化处理求解得到SDI:

1.2 水文干旱特征值与重现期定义

设定SDI=－1为游程的截断水平提取水文干旱特征值:干旱历时D、干旱强度I和干旱烈度S(图1).应用Copula函数构建干旱历时和干旱强度两变量的联合分布模式，推算其相应重现水平值，进而计算条件概率.

边缘分布干旱历时和干旱强度的重现期TD、TI公式分别为［10］:

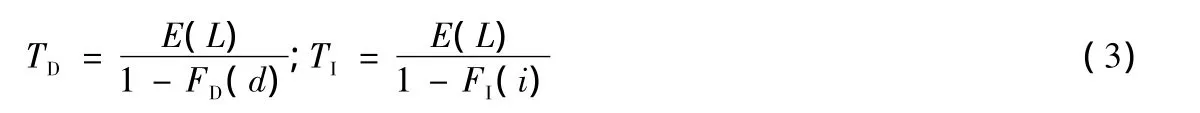
式中，E(L)为干旱时间间隔的期望值.

联合重现期To:

同现重现期Ta:

条件概率分布:

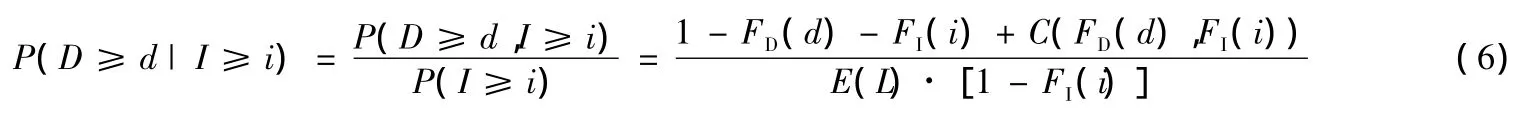
式中，P(D≥d|I≥i)为超值累积条件概率分布，可定义为遭遇概率或风险概率，其倒数即为条件(或遭遇)重现期.同理可计算P(I≥i|D≥d)的遭遇概率和条件重现期.

2 实例研究

2.1 研究背景与SDI指数统计分析

图1 干旱事件特征描述Fig.1 Characterization of drought events

干旱历来是广东三大心腹大患(洪涝、干旱、风灾)之一.近十几年来全球气候变化异常，降水变率增大，时空分布愈加不均，干旱趋于增强.其中，1998下半年至1999年广东曾出现夏秋冬春连旱现象，其引发的重大灾害成为社会普遍关注的问题.

珠江流域西江水系源于云南沾益县马雄山，东流至广西梧州汇桂江后始称西江，流入广东经珠江三角洲的磨刀门、鸡啼门、虎跳门和崖门注入南海，平均年径流量为2300×108m3.马口水文站位于西、北江三角洲河网区的顶端，作为国家重点水文监测站是西江进入河网区前必经的第一关隘，掌握和预测马口水文站的水情是做好西北江三角洲防洪防旱工作的关键.1990s以来，珠江河口三角洲枯季咸潮活动呈现出越来越频繁、强度不断增大、影响范围越来越大和持续时间不断增加等新特点［18］.受此影响，位于西江主要入海通道的磨刀门水道沿岸的中山、珠海和澳门等城市枯季用水受到极大影响.

采用1959年1月到2009年12月马口水文站月径流量计算了径流干旱指数.对SDI的三个时间尺度的统计分析结果表明，1960s是最近数十年间西江发生旱情最严重的时段，1970s-1980s旱情缓解，1990s以来干旱出现频次又持续增大(表1).进一步从风险概率角度深入分析马口站的水文干旱特征有助于有关部门对西江三角洲枯季水资源进行规划管理，并可加深对咸潮发生与持续性的认识.

表1 不同时间尺度的水文干旱频次的年代际变化Tab.1 Interdecadal variation of different time scales of hydrological drought occurrence frequencies

2.2 联合分布计算与分析

对D和I样本都使用了三参数的Weibull概率分布函数［19］:

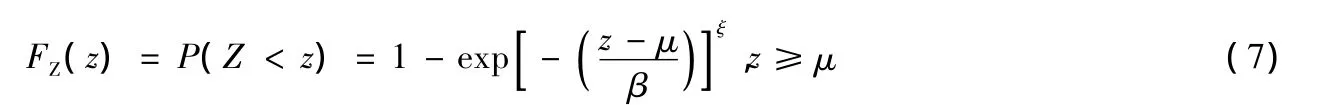
式中，ξ、β、μ分别为形态参数、尺度参数和位置参数.参数估计使用线性矩(L-矩)方法［20］.经验频率分布Pi使用 Gringorten 公式计算［21］:Pi=(i－0.44)/(n+0.12).拟合结果采用均方根误差(RMSE)、经验频率和理论频率拟合误差平方和(Q)和概率点据相关系数(PPCC)检验拟合优度.拟合的干旱历时和干旱强度的PPCC分别达0.994和0.992，其Weibull概率分布见图2.

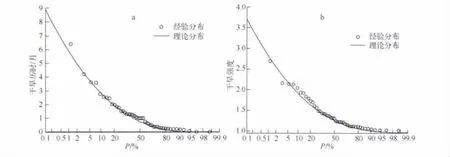
图2 干旱历时(a)和干旱强度(b)Weibull概率分布Fig.2 Weibull distribution of drought duration(a)and drought intensity(b)

统计的干旱历时和干旱强度之间的秩相关系数为0.617，说明二者之间存在高关联性.选择Archimedean 族4 种 Copula函数:Gumbel-Hougaard Copula、Clayton Copula、Ali-Mikhail-Haq Copula和 Frank Copula，通过Genest-Rivest图示方法［22］、均方根误差(RMSE)准则法和AIC信息准则法等拟合优度检验方法择优构建干旱变量D和I的联合概率分布模型，进而推算其重现水平和风险概率.

由相关性指标法计算的两个变量的联合概率分布Copula函数的参数θ等于2.611，利用AIC、RMSE检验其拟合优度的结果见表2.

表2 4个Copula函数的参数及其拟合优度指标对比Tab.2 Parameters of four Copula functions and evaluation indices of goodness of fit

根据拟合优度评价指标，选择两样本中AIC和RMSE最小、Genest-Rivest图示方法Kt-Ke关系图中点据和理论直线最接近45°对角线的Gumbel-Hougaard Copula作为联合概率分布的连接函数(图3).由于Gumbel-Hougaard Copula函数具有描述变量之间上尾正相关的性质，适用于干旱事件的概率分析.择优构建的干旱历时和干旱强度联合概率分布模式如下:

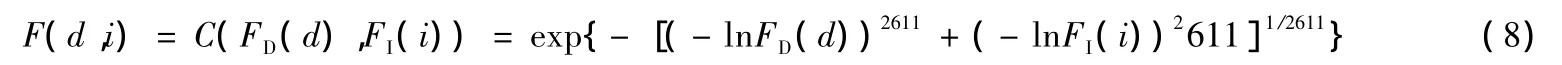
2.3 干旱历时和干旱强度联合分布的重现水平

由二变量Gumbel-Hougaard Copula联合分布计算的干旱历时和干旱强度的不同重现期可见，重现期为5～10年的干旱历时约2～3个月，相应的干旱强度介于1.5～2.0之间，即可达到重旱级别(表3).重现期为20年情况下，干旱历时约4个月，干旱强度即可达到特旱级别.50年、100年一遇的水文干旱历时分别约为5个月、6个月.

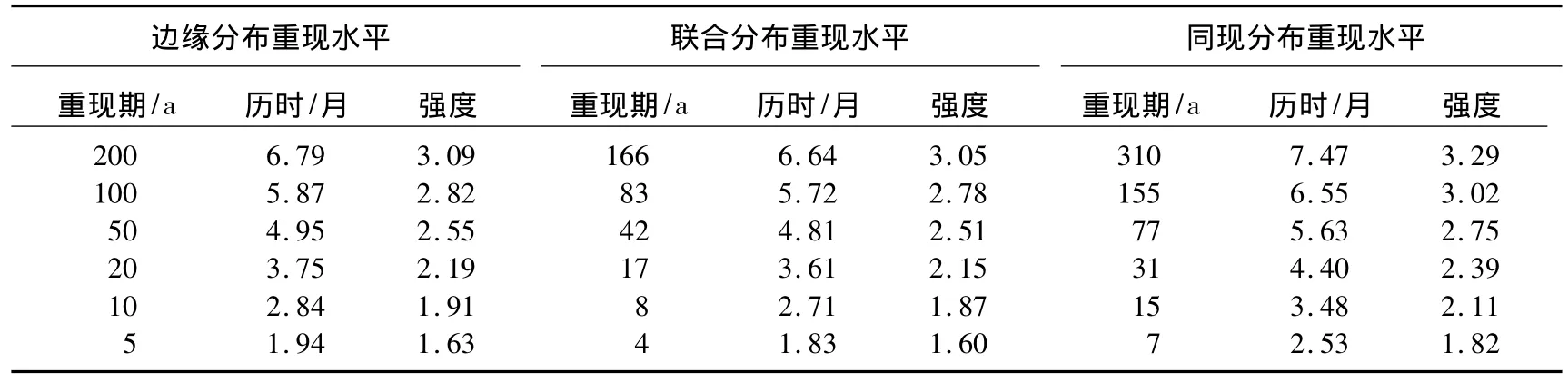
表3 干旱历时和干旱强度的不同重现水平值Tab.3 Different return level values of drought duration and drought intensity

由联合分布推算的干旱历时和干旱强度重现水平值分别略小于其相应的边缘分布的重现水平值，同现分布条件下推算的干旱历时和干旱强度重现水平值分别略大于其相应的边缘分布的重现水平值，联合分布和同现分布推算的重现水平值可视为单变量重现水平值的上下限，这样有助于对水资源工程建设投入与风险管理进行综合考虑.

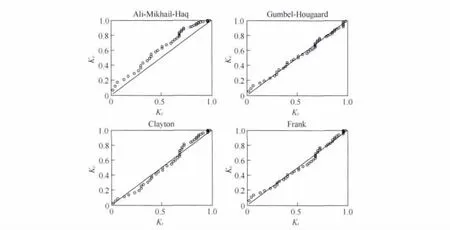
图3 4种Copula函数拟合对比Fig.3 Comparison of fitness of four theoretical and empirical Copulas

2.4 干旱历时和干旱强度条件分布与遭遇概率

干旱历时和干旱强度P(I≥i|D≥d)和P(D≥d|I≥i)两个条件概率分布见图4，干旱历时D为2、3、4、5、6、7 月和干旱强度 I为 1.63、1.91、2.19、2.55、2.82、3.09(分别对应重现期 5、10、20、50、100、200 年)之间的组合遭遇概率计算结果见表4.

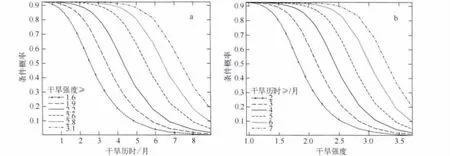
图4 干旱历时(a)和干旱强度(b)条件概率等值线分布Fig.4 Isograms distribution of conditional probabilities of drought duration(a)and drought intensity(b)

干旱历时和干旱强度遭遇概率表明:1)对特定干旱强度或干旱历时，随干旱历时的加长或干旱强度的加大，二者的遭遇概率明显增大，表明出现干旱历时或干旱级别的风险迅速增大.例如，20年一遇的干旱强度值为 2.2，其与干旱历时为 2、3、…、7 个月的遭遇概率分别为 23.5%、45.6%、…、92.0%，条件重现期介于1～4年之间;2)二者相关性强:同时增大干旱强度和干旱历时，二者大致仍保持在66% ～71%之间的高遭遇概率水平;3)随着干旱历时或干旱强度的加大，其与特定干旱特征值的遭遇概率随之递减.例如，干旱历时从2个月增大至7个月，其与干旱强度1.63的遭遇概率从66.6%降至2.1%，条件重现期大约介于1.5～48.2年之间，这进一步佐证了高的干旱级别通常与长的干旱历时相关联.综上分析表明，对应于特定干旱历时出现干旱级别(中旱、重旱、特旱)或特定干旱强度下出现干旱历时的条件概率分布实际上给出了干旱特征概率意义上的诊断预测，此对于枯季西北江三角洲的水资源的调度管理与调淡水压咸潮提供了有实质意义的信息.

表4 干旱历时和干旱强度遭遇概率Tab.4 Encounter probabilities of drought dura tion and drought intensity

3 结论

本文对西江下游马口水文站61年的径流干旱指数SDI提取干旱特征值，进而基于二变量Copula函数构建水文干旱特征值——干旱历时和干旱强度的联合分布模式，获得以下主要结论:

1)择优检验表明，采用Archimedean类的Gumbel-Hougaard Copula函数较好地构建了干旱历时和干旱强度的联合分布模式.

2)5～10年一遇的水文干旱即属重旱级别，干旱持续约2～3个月.20年一遇即达特旱级别，干旱持续约4个月.

3)联合分布和同现分布推算的重现水平值可作为干旱历时或干旱强度重现水平值的上下限，此有助于对枯季水资源工程建设与风险管理的综合考虑.

4)干旱历时和干旱强度条件概率分布表明，二者具有很强的相关性，其为特定干旱历时与水文干旱级别(中旱、重旱、特旱)或特定干旱强度与干旱历时之间的对应关系提供了概率意义上的干旱特征诊断与预测.

［1］Richard R，Heim Jr著.周跃武，冯建英译.美国20世纪干旱指数评述.干旱气象，2006，24(1):79-89.

［2］耿鸿江，沈必成.水文干旱的定义及其意义.干旱地区农业研究，1992，10(4):91-94.

［3］Fleig AK，Tallaksen LM，Hisdal H et al.A global evaluation of stream flow drought characteristics.Hydrology and Earth System Sciences，2006，10:535-552.

［4］周玉良，袁潇晨，金菊良等.基于Copula的区域水文干旱频率分析.地理科学，2011，31(11):1383-1388.

［5］陆桂华，闫桂霞，吴志勇等.基于Copula函数的区域干旱分析方法.水科学进展，2010，21(2):188-193.

［6］许月萍，张庆庆，楼章华等.基于Copula方法的干旱历时和烈度的联合概率分析.天津大学学报，2010，43(10):928-932.

［7］马明卫，宋松柏.椭圆型Copulas函数在西安站干旱特征分析中的应用.水文，2010，30(4):36-42.

［8］张 雨，宋松柏.Copulas函数在多变量干旱联合分布中的应用.灌溉排水学报，2010，29(3):64-68.

［9］闫宝伟，郭生练，肖 义等.基于两变量联合分布的干旱特征分析.干旱区研究，2007，24(4):537-542.

［10］Shiau J.Fitting drought duration and severity with Two-Dimensional Copulas.Water Resources Management，2006，20(5):795-815.

［11］尹正杰，黄 薇，陈 进.水库径流调节对水文干旱的影响分析.水文，2009，29(2):41-44.

［12］袁 超，宋松柏，荆 萍.极限水文干旱历时概率分布解析法研究.西北农林科技大学学报，2008，36(7):212-218.

［13］Salas JD，Chongjin F，Cancelliere A et al.Characterizing the severity and risk of drought in the Poudre River.Journal of Water Resources Planning and Management，2005，131(5):383-393.

［14］蔡明科.关中地区水文、气象干旱特征对比研究.灌溉排水学报，2003，22(6):33-37.

［15］袁文平，周广胜.标准化降水指标与Z指数在我国应用的对比分析.植物生态学报，2004，28(4):523-529.

［16］Seiler BA，Hayes M，Bressan L.Using the standardized precipitation index for flood risk monitoring.International Journal of Climatology，2002，22:1365-1376.

［17］Nalbantis I，Tsakiris G.Assessment of hydrological drought revisited.Water Resources Management，2009，23(5):881-897.

［18］胥加仕，罗承平.近年来珠江三角洲咸潮活动特点及重点研究领域探讨.人民珠江，2005，2:21-23.

［19］Hosking JRM.L-moments:Analysis and estimation of distributions using linear combinations of order statistics.Royal Statistical Society，1990，52(1):105-124.

［20］Seguro JV，Lambert TW.Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis.Journal of Wind Engineering and Industrial Aerodynamics，2000，85(1):75-84.

［21］郭生练，叶宁泽.论水文计算中的经验频率公式.武汉水利电力学院学报，1992，25(2):38-45.

［22］Genest C，Rivest L.Statistical inference procedures for bivariate Archimedean copulas.Journal of American Statistical Association，1993，88:1034-1043.