MPI下三维FDTD并行运算的分析与实现

宋永，杨阔

（阿坝师范高等专科学校 四川 汶川 623002）

1966年K.S.Yee首先提出的一种以Maxwell方程为基础的解决电磁场问题的数值计算方法[1]____时域有限差分法（Fnite Difference Time DomainFDTD）。FDTD算法将Maxwell方程中的两个旋度方程直接转化为差分形式，将电磁场进行空间和时间上的离散化，得到电磁场演化的迭代方程组，实现在一定体积内和一段时间上对连续电磁场的数据取样压缩。

在计算技术的迅速发展下，时域有限差分法被广泛接受和应用。但是随着计算量的增大和问题的复杂化，FDTD的实现和优越性的发挥也受到硬件的极大限制。原因是其算法稳定性要求空间网格的最大尺寸应小于波长的十分之一，计算时间又正比于网络总数处理电大目标电磁问题时所需内存很大。这使得在当前的PC机计算能力下，FDTD算法仅在低频范围获得了较多应用，在分析电大目标电磁问题中受到很大限制。而采用并行FDTD算法是解决这一问题的有效途径之一，从串行计算到并行计算可以使计算能力大幅度提高。

1 FDTD并行计算环境简介

FDTD算法本身具有适合于开展并行运算的优势[2]：由于FDTD方法中每一网格点的电场（磁场）分量的迭代公式只与它本身上一时刻的场值和周围网格磁场（电场）上半个时间步的值有关，而与计算区域内其他远端网格点的场量没有直接关系（如图1）。因而利用FDTD的这种局限性可以将FDTD区域在空间上分割成若干个子区域分别进行计算，这一点与并行运算的思路是统一的。

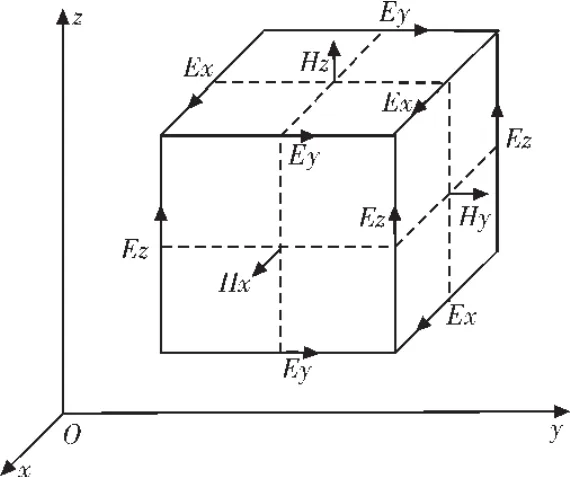
图1 FDTD算法中Yee氏网格Fig.1 Yee of FDTD arithmetic

1.1 并行计算机——曙光4000A

曙光4000系列是面向网格计算的高性能计算机系统，它采用网格技术、体系结构以构件性（Component）、标准性（Standard）、协作性 （Coorcdinate）为基准采用了服务化（Service）、安全化 （Secnrit）、专 业 化 （Specialization）、智 能 化（Intelligence）的技术。曙光4000A是曙光系列中计算速度最快的一种系统[3]。

1.2 MPI消息传递机制

消息传递技术MPI（Message Passing Interface消息传递接口）

MPI是一种在专业计算机领域使用得比较广泛的技术，是全球工业、政府和科研部门联合推出的适合进程间进行标准消息传递的并行程序设计平台；是目前应用最广泛的并行程序设计平台。消息传递就是指并行执行的部分之间通过消息传递来交换信息、协调步伐、控制执行。消息传递一般是面向分布式存储结构但是它也可以适用于共享存储的并行机。

1.3 MPI的基本函数

MPI有6个最基本的函数这6个基本函数构成了一个完整的MPI程序所需例程的最小集。

1）MPI初始化：MPI-Init （&arge&argv） 该初始化函数在MPI应用程序的开始部分调用，它使应用程序中各个并行执行的任务获得初始信息。

2）返回通信域包含的进程个数：MPI-Comm-size（commsize）

3）返回当前进程标识如果有n个进程进程的标识号从0到n-1。

MPI-Comm-rank（comm.，rank）

4）消息发送：将首地址为buf的count个数据类型为datatype的数据由当前进程发送给denst进程。

intMPI-Send（void*bufintcountMPI-Datatypedatatypeintdest int tag MOI-Comm comm）

5）消息接收：从sounce进程接收 count个数据类型为datatpye的数据，并保存到首地址为buf的内存空间中。

Int MPI-Recv（void*bufint countMPI-Datatype datatype int sourceint tag MPI-Comm commMP-Status*status）

6） MPI结束：MPI-Finalize（）.

1.4 MPI程序流程设计

MPI环境的初始化和结束流程：在调用MPI例程之前各个进程都应该执MPI_Init进行初始化，接着用MPI_Comm_size函数来获取缺省组 （Group）的大小。调用MPI_Comm_Rank函数获取调用进程在缺省组中的逻辑编号（从0开始），然后进程可以根据需要向其他节点发送消息或接收其他节点的消息。经常调用的函数是MPI_Send和MPI_Revc，最后当不需要调用任何MPI进程后调用MPI_Finalize函数消除MPI环境进程，此时可以结束。

2 MPI下三维FDTD的并行分析和运算实现

2.1 FDTD的三维基础

在FDTD离散中，电场和磁场各节点的空间分布采用的是著名的Yee氏网格。这种电磁场分量的空间取样方式不仅符合法拉第电磁感应定律和安培环路定律的自然结构，而且这种电磁场各分量的空间相对位置也适合于麦克斯韦方程的差分计算，能够恰当地描述电磁场的传播特性。

在三维的PML介质中每个场分量分解为两个子分量。在笛卡尔坐标系中6个分量则变为12个子分量，记为Exy、Exz、Eyx、Eyz、Ezx、Ezy、Hxy、Hxz、Hyx、Hyz、Hzx、Hzy。 进行三维区域分割后，相邻空间是在一个面元上进行数据变换，这样数据的交换量便增大，同时时间并行也变得复杂。如图2所示的沿二轴的分割图，可以看出两节点需要交换的数据是与分割面平行的场量 Ey、Ez、Ey、Ez。

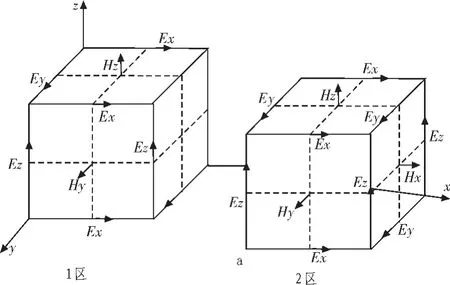
图2 三维空间区域分割后的场分布Fig.2 Regional segmentation of field distribution in three dimensional space after

2.2 用捆绑发送接收实现三维FDTD的应用

捆绑发送和接收操作把发送一个消息到一个目的地和从另一个进程接收一个消息合并到一个调用中，源和目的可以是相同的。捆绑发送、接收操作虽然在语句上等同于一个发送操作和一个接收操作的结合，但是它们可以有效地避免单独书写发送或接收操作时由于次序的错误而造成的死锁。这是因为该操作由通信系统来实现的，系统会优化通信次序从而有效地避免不合理的通信次序，最大限度地避免死锁的产生[4]。对于三维的FDTD并行程序，采用C++类函数来编程。在编程的过程中，主要涉及到头文件的设置，并行初始化激励源的加载，数据的传递以及对边界处的处理。对于吸收边界采用的是PML吸收边界，边界处电导率的大小与所处位置的关系式是 σ=σmax（ρ/d）n。σmax为边界处的最大电导率。ρ、d 分别是吸收边界的位置以及吸收层的厚度。n是ρ和σmax之间所遵循的关系。n=1是线性关系，本程序中采用的n=2的抛物线关系的。对于三维FDTD电场量E，磁场量H各有6个分量分别 Exy、Exz、Eyx、Eyz、Ezx、Ezy、Hxy、Hxz、Hyx、Hyz、Hzx、Hzy。

2.3 算法检验

在同一微分高斯脉冲激励源的前提下，分别采用串行、并行计算对同一问题。共计算500个时间步，可以得到每一点在不同时间步采用不同进程的场值幅值。对于同一个位置不同的时间步通过串行、并行得到的数据进行比较，采用了两个点的比较，点（25，30，30）和点（25，50，50）所得到的结果如图 3 所示。 左图是点（25，30，30），右图是点（25，50，50），由图示结果可知该并行程序中传递函数是正确的，整个程序是合理的。交换边界处的数据能进行互相接收和发送。

2.4 并行性能分析

并行计算的目标是使用p个处理器执行程序并获得比在单个处理器上高p倍的性能。顺序执行时间和并行执行时间之比称作加速比[5-6]。

加速比（Sp）=串行执行时间（Topt）/并行执行时间（Tp）

并行计算的效率（也称作处理器使用率）是加速比除以处理器个数：

效率（Ep）=加速比（Sp）/p

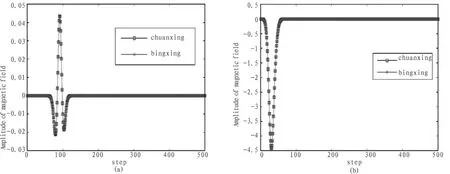
图3 同一点不同时间步的磁场幅度值Fig.3 At the same time steps of different magnetic field amplitude values

为了达到加速比Sp，并行执行时间必须是串行执行时间的l/p。因为仅有p个处理器，这意味着每个处理器必须分配到同样数量的工作。所有处理器在并行执行全过程中都必须在执行程序，而且算法在并行化过程中不能引入额外的操作。

在并行计算中，通信开销已经成为影响计算机效率的一个原因，这是因为每个处理机要独立管理自己的进程。为了达到较高的加速比，并行程序面临的一个很重要的问题就是负载平衡。它是指合理的在处理器之间重新分配负载平衡，达到系统的综合性能最优。一般情况下，根据各节点的性能不同应该承担不同规模的工作。计算速度快及内存大者应承担较大的任务量，反之则承担较小的任务量，这样可以避免快节点等待慢节点同步而造成的计算时间浪费。负载平衡过程必须在平衡计算能力和通讯开销的基础上平衡各节点的负载。以PML作为吸收边界的FDTD并行算法则是一种典型的同步并行算法。每一个时间步即是控制全局的并行时钟，不同的进程在每一个时间步中都要严格的按照FDTD迭代方式进行电场、磁场的数据交换。因此每个进程所承担的计算量负载的平衡是提高FDTD并行算法效率的关键之一。

2.5 并行效率的分析

对于三维的自由空间，点源辐射可以用数值比较解决问题。文中采用的是计算500个时间步的方式，分别用串行和并行时间来比较其效率。消息的发送和接收采用MPI捆绑式的堵塞式且对不同的网格大小进行计算，时间单位是s。其中np=2采用的是一维分割，np=4采用的是二维分割，np=8采用的是三维分割，计算结果如表1所示。

对表中的数据进行分析：对于50×50×50串并行所用时间进行比较，随着进程的增多所耗时间也是成倍的增加。加速比sp＜1，此时的网格大小只是适用于串行不适合并行计算；对于网格 100×100×100、200×200×100、200×200×200 采用串行和并行运算。对于np=2的墙上时间进行比较，可以得到此时均可以得到sp＞1，则该网格是适合并行算法的；对于100×100×100，采用不同进程所需要的时间以及得到的加速比进行比较可以得到：采用一维分割时加速比Sp＞1，但是对于二、三维分割方式，加速比是小于1的。由表1可知，对于200×200×100采用二维分割能得到最大的加速比。对于200×200×200的网格，三维分割才可以达到最大的加速比，其值高达2.214。这是因为墙上时间由两部分组成：空间计算时间和通信时间。加速比的高低取决与这两者的比例，因此可以得出：

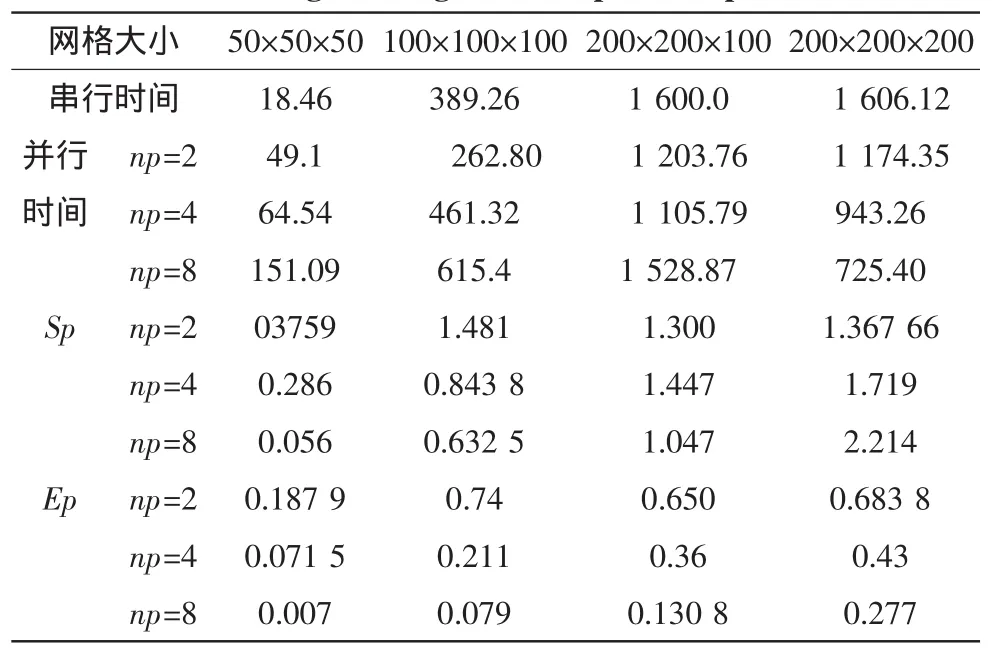
表1 不同网格采用不同进程运行的结果Tab.1 Different grid using different process operation results

1）当计算的网格数比较小的时候，比如50×50×50时，由于通信也需要一定的时间导致整个空间的计算时间比通信时间要小，采用并行算法时要比串行时间长，得到的加速比小于1。采用的并行进程越多通信量成倍的增加，则所得到的加速比也是成倍的降低效率的；

2）只有计算网格达到一定的数目，比如 100×100×100时，采用并行计算才能优于串行计算达到加速比Sp＞1。此时在各个进程之间的通信时间要小于计算时间，计算时间是主要的。所以并不是所有的并行计算都要比串行计算快的。

3）当采用并行计算的时，空间的分割方式与网格划分的多少是有关的。

①当整个计算空间不是太大时，100×100×100通信时间在整个墙上时间占了一个较大的分量，那么此时采用最简单的一维分割采用较小数目的进程则能减小通信时间。比如两个进程时，此时得到的加速比是要高十多个进程的。如果此时采用多个进程将导致加速比Sp＜1的情况出现。

②当整个计算网格数大到一定的程度时，比如200×200×200，由于计算时间占了很大的一部分，相对通信时间的分量减小，无论采用几维的分割方式，Sp＞1的趋势是不会改变的。此时采用三维的分割方式多个进程并行可以得到最大的加速比和效率。

③采用三维的分割，每维上的进程数是要根据实际情况来选择的，并不是越多越好，每增加一个进程就是增加一倍的通信时间。对于实际计算中，计算步是成千上万的网格数，也是多于106个。此时采用合适的并行计算，根据模型采取合适的分割方式以及各个方向上的进程数显得尤为重要，恰当划分空间网格可以达到一个最大的加速比。

3 结束语

文中主要用数值说明了基于MPI消息传递机制的FDTD并行算法分析网格数、进程数、分割方式，三者对效率的影响，定量的给出三者的关系。网格数比较小的时候适合串行。只有网格数达到一定的数目，并行才能优于串行计算，而此时采用不同维数并行计算对效率影响比较大，效率的提高依赖于网格划分方式和进程数。文中给出了网格数以及适合的划分方式和进程数。这将为以后进行并行计算如何选择一个合适的分割方式和进程数提供一个参考。

[1]Yee K S.Numerical solution of initial boundary value problems involving Maxwell equa-tion in isltropic media[J].IEEE Trans.Antennas Propagat.，1966，14（3）:302-307.

[2]Shlager K L.，Schneider John B.Selective survey of the finitedifference time-domain literature[J].IEEE Antennas&Pro Pagation Magazine，1995，37（4）：53-57.

[3]都志辉.高性能计算并行编程技术-MPI并行程序设计[M].北京：清华大学出版社，2001.

[4]李太全.时域有限差分算法的MPI实现与效率分析 [J].长江大学学报：自科版，2007，4（1）:32-34.

LI Tai-quan.Implementation of FDTD in MPI and analysis on efficiency[J].Journal of Yangtze University：Natural Science Edition，2007，4（1）:32-34.

[5]Michael J.Quinn.Parallel Programming in C with MPI and OpenMP[M].北京：清华大学出版社，2003.

[6]Quinn M J.MPI与OpenMP并行程序设计 （C语言版）[M].北京：清华大学出版社，2004.