基于数值方法的内超环面齿轮齿廓离散建模

洪 玫， 姚立纲

（福州大学机械工程学院，福建 福州 350108）

基于数值方法的内超环面齿轮齿廓离散建模

洪 玫， 姚立纲

（福州大学机械工程学院，福建 福州 350108）

超环面行星蜗杆传动系统中的关键零件内超环面齿轮的齿面是一种复杂的空间曲面。为了实现复杂曲面的数控加工和采用有限元方法对其进行接触分析时，能否获得精确的内超环面齿轮的实体模型是解决问题的关键。本文针对内超环面齿轮数字化建模问题，根据内超环面齿轮的数学模型，对其螺旋齿面进行网格划分，提出基于数值方法的内超环面齿轮离散建模方法。该方法采用截平面蔟将内超环面齿轮模型离散成数据点云，从而获得内超环面齿轮离散模型，为后期的复杂曲面插值重构提供了基础。

超环面行星蜗杆传动；内超环面齿轮；离散建模；实体模型

超环面行星蜗杆传动，如图1所示，由中心蜗杆、行星蜗轮、内超环面齿轮、行星架以及滚动体组成，它将蜗杆传动和行星传动有机地结合成一体，是一种滚动啮合的行星蜗杆传动。这种传动机构工作时，运动由中心蜗杆轴输入并带动行星蜗轮旋转，当内超环面齿轮不动时，行星蜗轮作环状的螺旋运动，并通过与输出轴固连的行星架实现运动的输出。运动过程中，行星蜗轮既绕自身轴线旋转又绕中心蜗杆轴线公转，形成了内超环面齿轮。国内外学者对超环面行星蜗杆传动的啮合理论[1-2]，加工制造[3-4]、承载能力[5-6]和摩擦、磨损[7-12]等方面进行了深入研究。

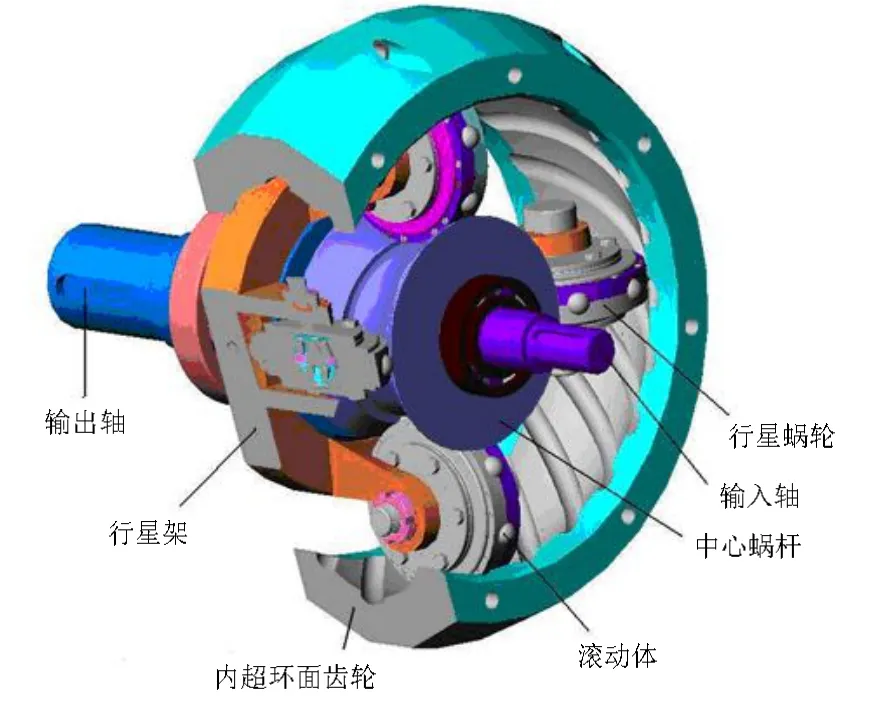
图1 超环面行星蜗杆传动

超环面行星蜗杆传动中内超环面齿轮和中心蜗杆的齿廓都是复杂的空间曲面，为保证超环面行星蜗杆系统的传动精度，建立内超环面齿轮和中心蜗杆的齿廓的精确数字化模型是亟待解决的关键问题之一，也是啮合传动领域的研究热点。目前，内超环面齿轮和中心蜗杆的实体模型主要是采用solidworks，Pro/E等三维CAD软件来建立[13]。该方法是利用特定截面齿廓,根据一定的路径扫描生成内超环面齿轮和中心蜗杆齿面的。以内超环面齿轮建模为例，首先，根据内超环面齿轮齿面的螺旋线方程，通过数值计算获得螺旋线上一系列点的坐标值，将坐标值导入solidworks，得到螺旋线，然后在螺旋线法平面上画出内超环面齿轮齿面的法面齿形，将此法面齿形沿螺旋线扫面切除，即完成对内超环面齿轮的三维实体建模。虽然内超环面齿轮齿面的法面齿廓是圆，但在其他任何平面内，其齿廓却是一条空间曲线，因此，采用该种方法所生成的内超环面齿轮实体模型存在理论误差。

关于其他复杂曲面齿轮三维几何建模的国内外主要研究方法如下，国外Litvin[14]、QiFan[15]分别通过接触分析，加工原理建立了螺旋锥齿轮齿面数学模型，但没有详细的三维实体模型建立过程。国内王裕清[16]等根据弧齿锥齿轮齿面4条边界信息点构造三维齿面模型，提出了运用NURBS进行曲面逼近，从而实现轮齿实体模拟的方法。唐进元[17]等利用虚拟制造方法模拟准双曲面齿轮加工过程，对其齿面和过度齿面包络曲线蔟进行曲面拟合得到含过渡曲面的准双曲面齿轮的三维几何模型。谭昕[18-19]等运用数值方法得到平面二次包络蜗轮理论齿面的离散模型，并采用三角B-B曲面片进行插值重构建模。

为了提高内超环面齿轮实体模型的精确性，从而更好的实现复杂曲面数控加工，本文以网格状曲面为基础，提出基于数值方法的内超环面齿轮齿廓离散建模方法。

1 内超环面齿轮的数学模型

内超环面齿轮齿廓离散建模的关键是齿廓数学模型的正确建立，如图2所示，为剖视的内超环面齿轮三维实体模型。它由螺旋齿廓齿面、旋转曲面和两个端面组成。

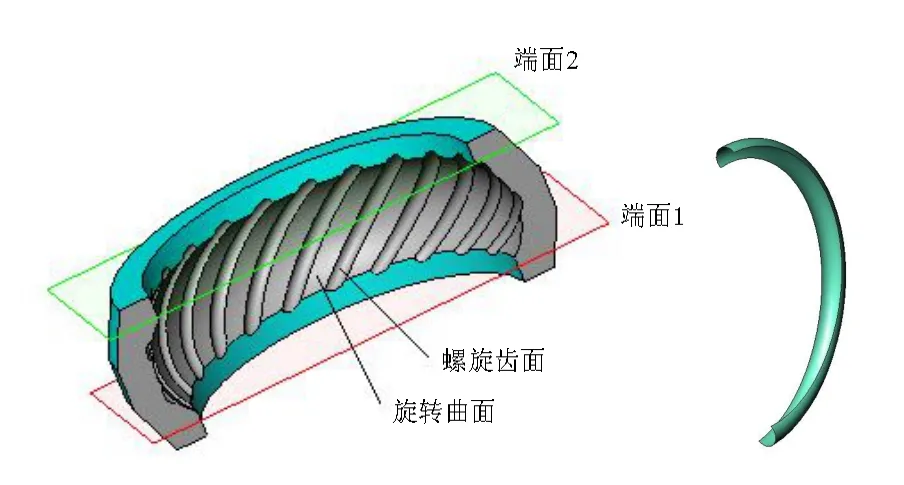
图2 剖视的内超环面齿轮三维实体模型和单个螺旋齿面

1.1 内超环面齿轮螺旋齿面的数学模型

内超环面齿轮的螺旋齿面)3(Σ是由行星蜗轮齿面)2(Σ的运动包络而成的。如图3所示，建立的空间坐标系，表示行星蜗轮与内超环面齿轮的啮合情况。在图3中，内超环面齿轮到行星蜗轮的中心距为0a， ),,(3333kjiS为内超环面齿轮的参考坐标系， ),,(2222kjiS为行星蜗轮的参考坐标系；),,(3333′′′′kjiS为内超环面齿轮的动坐标系，与内超环面齿轮固连，),,(2222′′′′kjiS为行星蜗轮的动坐标系，与行星蜗轮固连。动坐标系3′S、2′S分别跟随内超环面齿轮、行星蜗轮绕轴3′k、2′k以3ω、2ω的角速度旋转，3φ、2φ分别为螺旋齿面)3(Σ、)2(Σ相对于它们的参考坐标系3S、2S的转角。

图3 行星蜗轮与内超环面齿轮啮合坐标系

行星蜗轮的球形轮齿是内超环面齿轮齿廓的包络母面，如图4所示为其在空间坐标系2'S中的位置， ),,(0000kjiS为球形滚动体的参考坐标系，),,(0000′′′′kjiS为球形滚动体的动坐标系，与球形滚珠固连。球形滚珠半径为ρ，u、v为滚珠的球面参数。

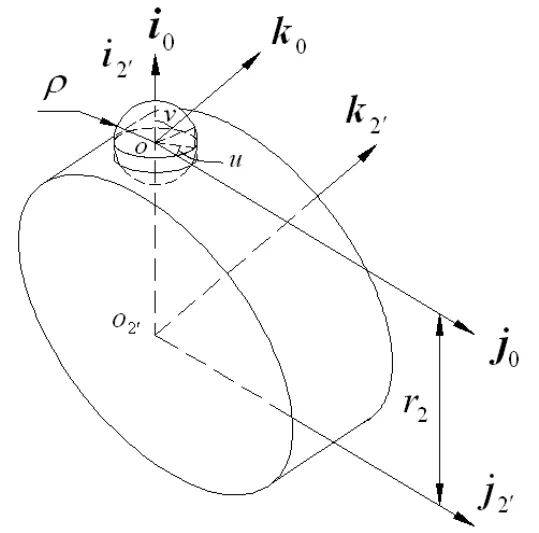
图4 行星蜗轮与内超环面齿轮啮合坐标系

由图4经坐标变换，可得行星蜗轮轮齿在坐标系2S′中的方程为：

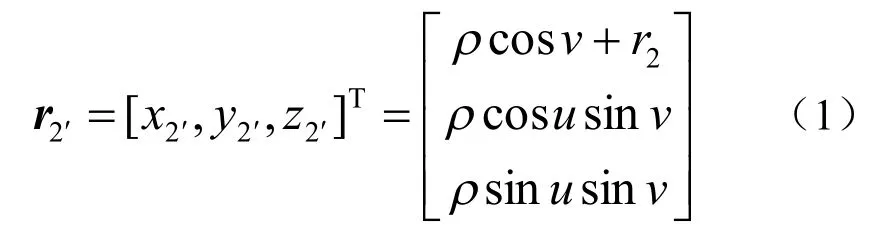
由齿轮啮合原理[20]，两共轭齿面Σ(2)、Σ( 3)的啮合方程、啮合函数为：

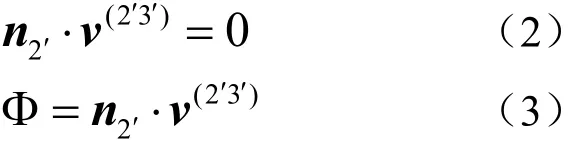
式(2)、式(3)中，n2′为行星蜗轮与内超环面齿轮啮合点处的公法幺矢；v(2′3′)为行星蜗轮与内超环面齿轮在啮合点处的相对速度矢量。可以推导出内超环面齿轮螺旋齿面方程如下：

式(1)、式(4)中，r2、i23及a0都是已知常数，u、v均为滚珠球面参数。内超环面齿轮齿面方程是关于 (φ3, φ2)的参数方程。u是随行星蜗轮转角φ2而改变的变量，当给定一个φ2的范围，u的取值范围随之确定。v的取值范围是[- π / 2,π / 2]。

1.2 内超环面齿轮旋转曲面的数学模型

内超环面齿轮旋转曲面方程为：

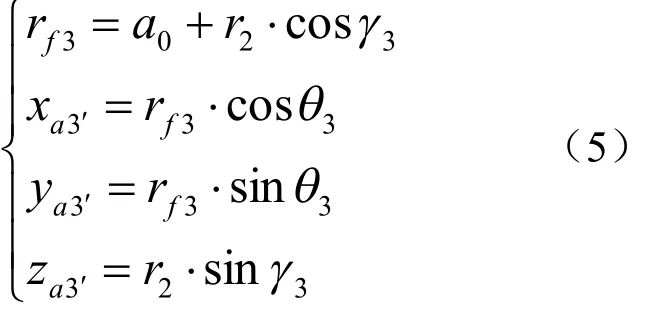
式(5)中，r2是行星蜗轮计算圆半径，γ3=[- π 3, π 3]，θ3=[0,2π]，γ3是结合内超环面齿轮包容行星蜗轮的包角spE来取值的，而3θ则根据内超环面齿轮绕其轴线旋转一周的变化范围所确定的。

2 内超环面齿轮螺旋齿面网格的划分

内超环面齿轮螺旋齿面是复杂的空间曲面，为了获得齿面精确的数字化模型，本文采用网格状曲面模型来表达其理论齿面，如图5所示。所谓网格状曲面，就是用满足一定精度要求的离散的小曲面片来近似表达整张曲面。根据内超环面齿轮接触线方程，提取网格曲面信息点，从而建立网格状曲面模型来近似表达内超环面齿轮理论螺旋齿面。

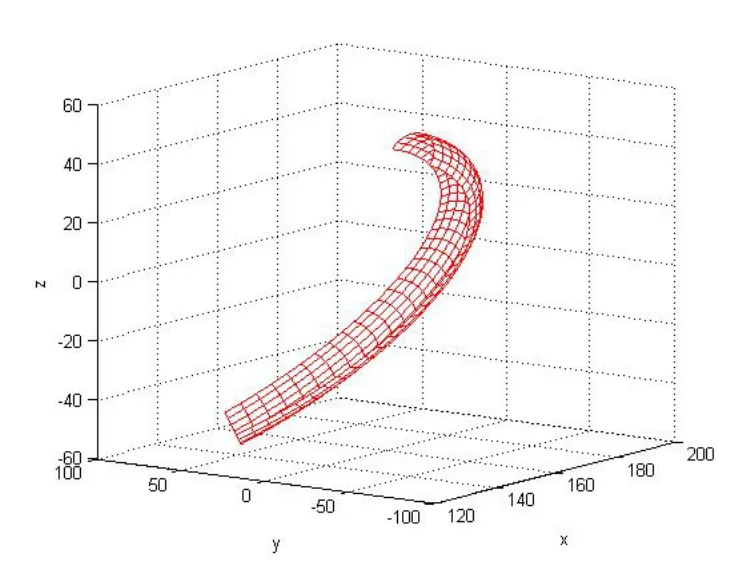
图5 内超环面齿轮螺旋齿面网格状模型（单齿）

2.1 网格曲面信息点的确定

为了将内超环面齿轮螺旋齿面离散化，可采用与内超环面齿轮端面平行的截平面蔟如图6所示与其理论接触线求交来获得齿面点。

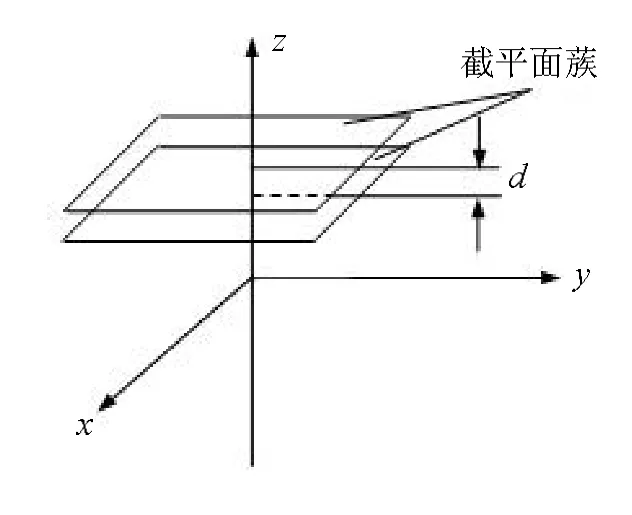
图6 截平面蔟位置

若用n个截平面与齿面n条接触线求交，可获得m×n个齿面信息点，这些齿面信息点就构成了内超环面齿轮螺旋齿面的离散数据点云。决定这些离散小曲面片的大小和位置的就是这些离散数据点，用矩阵形式来表示即为：

可以通过网格加密来保证内超环面齿轮螺旋齿面的离散模型精度，即通过改变截平面的个数n和内超环面齿轮接触线的条数m来控制网格间距，网格间距越小，误差越小。

2.2 螺旋齿面离散数据点的求解算法

如图 6所示，设kz为截平面在z轴上的截距，则截平面方程为：

联立式(4)和式(6)，可获得内超环面齿轮螺旋齿面和截平面截交线的非线性方程组，即：

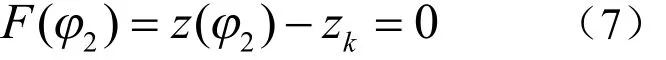
在给定截平面的情况下，运用对分法求解方程(7)

1） 确定有根区间

根据超环面行星蜗杆传动系统基本设计参数确定行星蜗轮转角φ2的工作范围[φ2a, φ2b]，分别计算F(φ2a)和F(φ2b)。将φ2的工作范围[φ2a, φ2b]分成n个单调区间，φ2i=φ2a+ih,h= ( φ2b-φ2a)/n，(i=1,…,n)，按步长逐步搜索，若F(φ2i)F(φ2i+1) ＜ 0，则确定了一个有根区间。

2） 对分法求方程的根

假设找到的有根单调区间为 [φ2a1, φ2b1]，取区 间 的 中 点 φm= ( φ2a1+ φ2b1)/2， 检 查F(φ2a1)F(φm) ＜ 0是 否 成立 。 若成 立， 则 取[φ2a1,φm] 为搜索区间，否则，取 [φm, φ2b1]为搜索区间，反复执行上述步骤，直到对分区间缩小到允许的误差范围之内。

根据根据上述算法，在Matlab中建立内超环面齿轮螺旋齿面单齿离散模型，因为内超环面齿轮有23个齿且均匀分布在其旋转曲面上，因此，将所得的单齿螺旋齿面离散模型阵列为23等分，从而得到内超环面齿轮螺旋齿面离散模型，如图7所示。

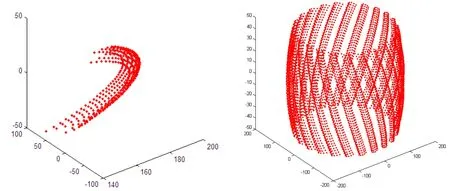
图7 内超环面齿轮螺旋齿面单齿和23齿离散模型

3 内超环面齿轮离散模型的建立

3.1 旋转曲面离散模型

采用相同的方法，根据内超环面旋转曲面方程，用截平面蔟和旋转曲面求交，可以获得旋转曲面离散信息点，在Matlab中建立内超环面齿轮旋转曲面离散模型，如图8所示。

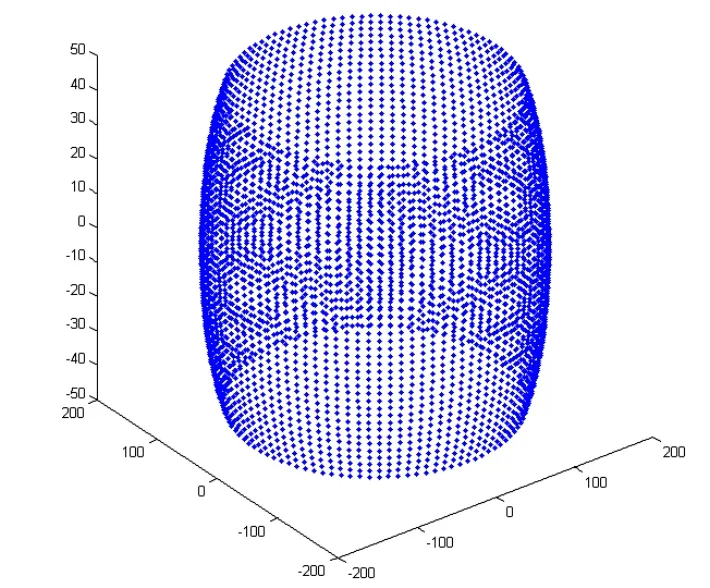
图8 内超环面齿轮旋转齿面离散模型

3.2 螺旋曲面和旋转曲面离散模型的合并与裁剪

为了获得内超环面齿轮的离散模型，必须将螺旋曲面和旋转曲面合并，合并后发现两个曲面有交叉，如图9所示。因此，必须裁剪掉这些多余曲面。只要找到旋转曲面和螺旋齿面的交线，然后将两条交线之间的多余曲面裁剪掉，即可获得内超环面齿轮离散整体模型。

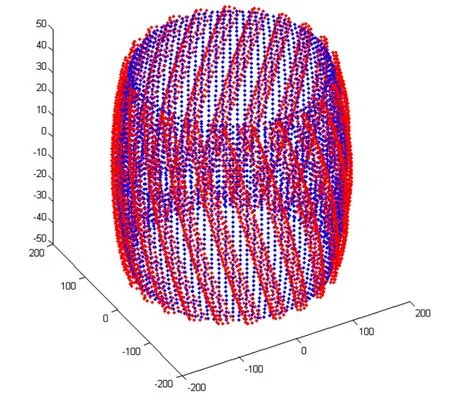
图9 内超环面齿轮离散合并模型

根据内超环面齿轮接触线方程，当取v=-π / 2和v=π / 2时，可得到两条边界线。这两条边界线是内超环面齿轮螺旋齿面的两个极限位置同时也是螺旋齿面和旋转齿面的交线，如图10所示。

指定一个截平面与旋转曲面和螺旋曲面都相交，比较同一截平面处边界数据点和旋转曲面数据点坐标的正切值，把正切值介于两边界数据点之间的旋转曲面数据点屏蔽。从而解决了螺旋曲面和旋转曲面合并后多余曲面的裁剪问题，如图11所示。

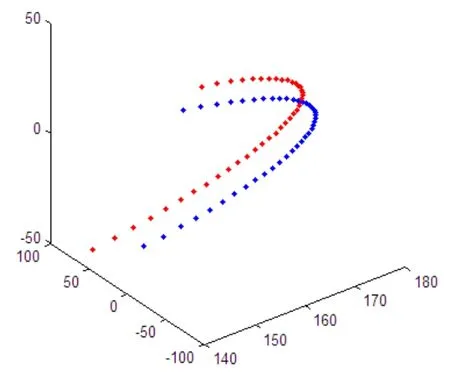
图10 内超环面齿轮螺旋齿面边界线

图11 内超环面齿轮离散模型

由上述提出的内超环面齿轮离散建模方法，本文利用南平南孚电池有限公司的 Marzak数控加工中心进行了内超环面齿轮的实际加工。图12所示为在 Marzak数控加工中心上粗铣内超环面齿轮内圆环螺旋面的照片，图13为精铣内超环面齿轮内圆环螺旋面的照片。图14为在数控加工中心中加工制造出来的内超环面齿轮的实物照片。

图12 内超环面内圆环螺旋面粗铣过程

图13 内超环面齿轮内圆环螺旋面精铣过程

图14 内超环面齿轮实物照片

4 结 论

齿形复杂的齿轮副的数字化造型一直是个难点，现有的商业化CAD软件solidworks，Pro/E等，建模的精度不够高。本文通过截平面法将内超环面齿轮模型表达为离散数据点云，从而获得了内超环面齿轮的离散模型。将提取的坐标数据点导入solidworks等三维建模软件进行后期的插值处理，可获得满足数控加工要求的高精度的三维数字化模型，为实现超环面行星蜗杆传动系统的数控加工提供了良好的基础。

[1]Yao Ligang, Dai Jian S, Wei Guowu, et al. Geometric modelling and meshing characteristics of the toroidal drive [J]. Transaction of ASME, Journal of Mechanical Design, 2005, 127(5)：988-996.

[2]Yao Ligang, Dai Jian S, Wei Guowu, et al.Comparative analysis of meshing characteristics with respect to different meshing rollers of the toroidal drive [J]. Mechanism and Machine Theory, 2006, 41：1237-1255.

[3]Yao Ligang, Dai Jian S, Huamin Li. Mathematical modelling and manufacturing of the internal toroidal tooth profile [J]. Journal of Mechanical Engineering Science, 2004, 218：1043-1051.

[4]Yao Ligang, Dai Jian S, Wei Guowu. Error analysis and compensation for meshing contact of toroidal drive [J]. Transaction of ASME, Journal of Mechanical Design, 2006, 128(3)：526-533.

[5]Peeken H, Troeder Chr, Cierniak S, et al. Entwicklung und konstruktion des toroidgetriebes [J]. Konstruktion,1979, 31(11)：421- 428.

[6]Peeken H, Troeder C, Tooten K H. Borechnung und messung der lastverteilung im toroidgetriebe [J].Konstruction, 1984, 36(3)：81- 86.

[7]许立忠, 黄 真. 超环面行星蜗杆传动摩擦理论研究[J]. 中国工程科学, 2002, 4(3)：63-67.

[8]许立忠, 杨育林, 黄 真. 超环面行星蜗杆传动弹流润滑状态研究[J]. 机械工程学报, 2002, 38(9)：114-117.

[9]许立忠, 张志慧, 闻 岩. 滚锥包络环面蜗杆传动磨损研究[J]. 润滑与密封, 2001, (6)：16-17, 19.

[10]许立忠, 杨盛福, 景常海. 滚锥包络环面蜗杆传动润滑研究[J]. 润滑与密封, 2001, (5)：31-32.

[11]Xu Lizhong, Huang Zhen, Yang Yulin. Contact stress for toroidal drive [J]. Trans of ASME, Journal of Mechanical Design, 2003, 125：165-168.

[12]Xu Lizhong, Huang Zhen, Yang Yulin. Mesh theory for toroidal drive [J]. Transaction of ASME, Journal of Mechanical Design, 2004, 126：551-557.

[13]魏国武. 超环面行星蜗杆传动的关键技术研究[D].福州：福州大学机械工程学院, 2004：9-27.

[14]Litvin F L. Determination of principal cruvatrues and contact ellipse for profile crowned helical gears [J].Journal of Mechanical Design, 1999, 121：107-111.

[15]Fan Q. Computerized modeling and simulation of spiral bevel and hypoid gears manufactured by gleason face hobbing progress [J]. Journal of Mechanical Design, 2006, 128：1315-1327.

[16]王裕清, 王小林, 梁 剑. 弧齿锥齿轮实体造型数学模型及其实现[J]. 中国机械工程, 2007, 18(14)：1660-1663.

[17]唐进元, 聂金安. 含过渡曲面的准双曲面齿轮精确三维几何建模方法[J]. 机械科学与技术, 2010,29(3)：358-363, 368.

[18]谭 昕, 周 红. 平面二次包络蜗轮齿面的插值重构建模[J]. 中国制造业信息化, 2005, 34(2)：88-91.

[19]谭 昕, 徐 林, 周 红. 基于数值方法的平面二次包络蜗轮齿面的离散建模[J]. 机械传动, 2005,29(3)：3-5.

[20]吴鸿业. 齿轮啮合理论[M]. 哈尔滨：哈尔滨工业大学出版社, 1979.

Discrete Modeling of the Tooth Profile of the Stationary Internal Toroidal Based on Numerical Method

Hong Mei, Yao Ligang
( School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou Fujian 350108, China )

The tooth surface of the stationary internal toroidal gear that is the key parts of the toroidal drive is a complex space curved surface. In order to realize the complex surface of the NC processing and using the finite element method for the contact analysis, whether obtaining the accurate entity model of the stationary internal toroidal gear or not is the key to resolving the problem. In this paper aiming at the stationary internal toroidal gear digital modeling problems,according to the mathematical model of the stationary internal toroidal gear, the grid division method of the helical tooth surface is given, the method of the stationary internal toroidal gear discrete modeling based on the numerical method is put forward. The method adopts cutting planes to scatter the stationary internal toroidal gear model into data point cloud, so as to get the stationary internal toroidal gear discrete model as the basis for later complex curved surface interpolation reconstruction.

toroidal drive; stationary internal toroidal gear; discrete modeling; entity model

TH 132

A

2095-302X (2013)04-0088-06

2012-10-29；定稿日期：2012-12-25

提高超环面行星蜗杆传动精度的研究，国家自然科学基金资助项目（50675035）；超环面行星蜗杆传动系统的修形设计与加工的研究，校科技发展基金项目（ 600621）

洪 玫（1980-），女，福建厦门人，讲师，博士研究生，主要研究方向为数字化设计。E-mail：ahiahm@sohu.com