一种用于双成像光刻中的版图分解算法
魏晗一,陆伟成
(复旦大学 专用集成电路与系统国家重点实验室,上海201203)
随着半导体技术的迅速发展,集成电路制造工艺已逼近22nm,并迈向更小尺寸和更高集成度.现时版图中的图形尺寸和图形间距,相对于现有工艺的光刻波长显得过小,光刻时光波将发生衍射,导致光刻后图形产生较大失真.由于以极端远紫外线光刻技术(extreme ultraviolet,EUV)为代表的下一代光刻工艺无论是在可应用的技术节点方面还是在量产能力方面都还未能满足业界需求[1],因此现有的193nm光刻工艺仍将被继续使用[2].现在,双成像光刻(double patterning,DP)技术是解决光刻后的图形畸变问题和提高光刻准确度的最有效的解决方案之一[3].双成像光刻技术将原版图合理地划分为2个子版图,使得每1个子版图中的图形间距(pitch)相当于原版图中图形间距的2倍,图形密度相当于原版图密度的通过分别使用2个掩模版进行2次光刻,将大幅度提高光刻后图形的准确度[4].在双成像光刻技术中,需要先进行版图分解(layout fracturing),即将版图中的多边形(polygon)图形分解为更简单的图形的集合.在1个版图中,多边形图形大多数是直角多边形(rectilinear polygon),即所有边都是水平或竖直方向,并与坐标轴平行(axis-parallel)的多边形,如图1所示;也有少数多边形包含部分斜边和斜角,在本文中将它们称为带斜角多边形(polygon with slant angles),如图2所示.然后对分解后的图形进行颜色分配(coloring).称间距小于给定的最小间距的两个图形之间产生了冲突(conflict),如图1中的圈中部分所示,需要给它们分配不同的颜色,表示它们将被分配在不同的子版图[5]中.版图分解工作是必须的,因为版图中的图形会存在自相冲突(self-conflict)的情况,如图1所示;另外,版图分解通过将版图中复杂的多边形分解为更简单的图形的集合,如矩形(rectangle)和不规则四边形(trapezoid)等,将简化后续的颜色分配工作.在颜色分配结束后,一些被分配为相同颜色的图形可以重新被合并为多边形,减少图形数目从而简化版图,同时减少切线(stitch)数目从而降低覆盖误差(overlay error)和线端缩短(line-end shortening)所导致的额外制造成本[6].在超大规模集成电路(Very Large Scale Integration,VLSI)领域,有许多研究关注将多边形分解为更简单的图形的集合,如在带障碍的时钟树中,通过将版图中的直角多边形障碍分解成矩形,在布线时只需考虑简单的矩形障碍,从而减小了布线算法的复杂度[7].直角多边形分解算法根据是否允许分解后的图形间彼此存在交叠(overlap)部分而分为覆盖(cover)算法和切割(partition)算法两类.在前人的研究中,主要有两类分解目标,一类是使分解后切线总长度最短[8],仅在切割算法中出现;另一类是使分解后矩形总数最少[9,10],在覆盖算法和切割算法中均存在.
1种简单直观并且被业界广泛采用的版图分解算法是单方向多边形切割算法[11],该算法应用到双成像光刻技术中时会产生2个问题,如图3所示.

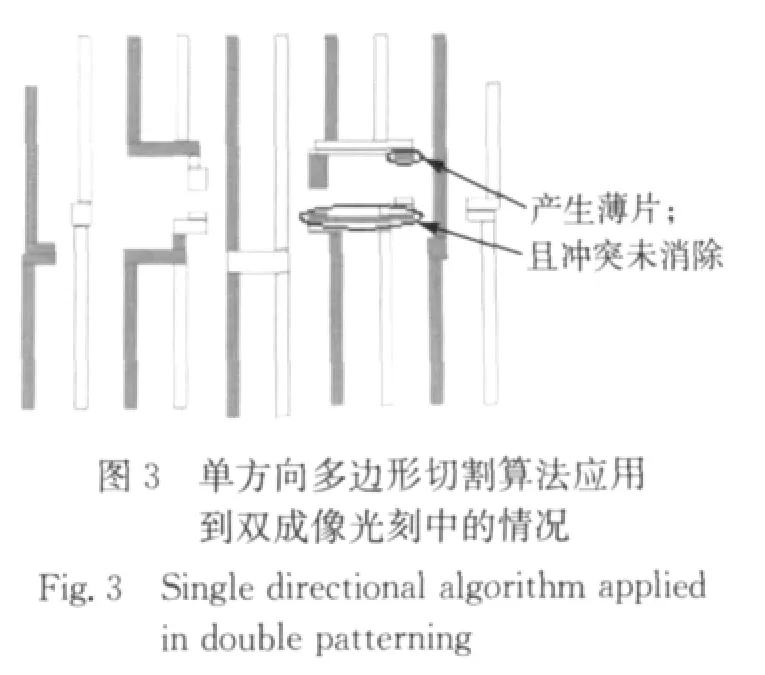
1)版图在分解后产生宽度小于版图工艺尺寸的图形,称之为“薄片”(sliver).如果经过颜色分配和合并工作后的图形依然属于薄片,会导致重要尺寸误差(critical dimension error),给掩膜和光刻带来很大挑战,如图3中圈中所示.
2)在经过颜色分配和合并后,版图中仍旧存在大量冲突,有关这1点将在下文通过实验具体说明.
显然地,将单方向多边形切割算法应用在双成像光刻技术并不合理.
文献[12]提出了1种使用射线-线段选择(ray-segment selection)的版图分解算法,近似最优地使分解后薄片总数最少,但仍旧未消除薄片.
如前文所述,现有的版图分解算法的目标有分解后切线总长度最短、分解后矩形总数最少和分解后薄片总数最少,然而,现有的版图分解算法在双成像光刻技术中不适用,有关这1点将在下1部分中具体说明.更为重要的是,分解后的图形中不存在工艺无法接受的薄片是能够正确进行双成像光刻的前提.现有的版图分解算法中,切割算法在分解后往往会产生薄片.
另外,文献[12]不允许分解后的图形间存在交叠,认为交叠部分在光刻时会发生过度曝光.但是文献[13]指出,交叠在双成像光刻中是可以接受的,并且如果分解后的图形间有交叠部分,能够解决光刻时由于覆盖误差引起的图形断开问题.文献[14]进一步通过实验证明足够的交叠部分能够消除两次光刻的覆盖误差所导致的图形失真的影响,并且当掩膜版同时沿x和y2个方向发生偏移(mask bias)时交叠能够起到稳定图形宽度的作用.可见分解后的图形间存在交叠是可以接受的,并且将有利于双成像光刻技术,而目前用于双成像光刻中的版图分解算法并没有引入交叠.
本文提出1种新的版图分解算法,用于双成像光刻技术,实现分解后的图形不存在薄片并解决光刻时由于覆盖误差引起的图形断开问题的前提,以减少颜色分配后的冲突总数为目标,主要通过在可接受的时间复杂度下减短分解后切线总长度,同时引入交叠.其中引入交叠将带来的优势是:1)消除薄片的产生;2)解决光刻时由于覆盖误差引起的图形断开问题;3)减少分解后的矩形数目,从而既能够减少冲突总数,又能够简化版图.
1 与现有算法比较
接下来将通过使用本文算法和现有的各种算法分别对版图中常见的一些多边形例子进行分解的情况进行比较,说明本文的版图分解算法优胜的方面.在下文的图中,虚线表示切线,阴影表示分解后图形间的交叠部分.显然地,和切割算法相比,本文算法通过引入交叠,在绝大部分情况中使分解后相连(connect)的图形在相连处有互相交叠的部分,首先能够解决光刻时由于覆盖误差引起的图形断开问题.
图4显示了使用本文算法和另两种现有算法对同1个多边形分解后的情况.可见在这个例子中,图4(a)单方向多边形切割算法[11]和图4(b)分解后切线总长度最短的多边形切割算法[8]都产生了光刻工艺所无法接受的薄片,如图4圈中所示,并且分解后矩形总数较多,将会增加冲突数目和版图制造成本;而图4(c)本文算法通过引入交叠:1)消除薄片的产生,确保版图符合光刻工艺要求;2)尽量减短分解后切线总长度,从而减少冲突数目;3)实现矩形总数最少,在减少冲突数目的同时也简化了版图,降低制造成本.
在图5多边形分解的例子中,图5(a)分解后矩形总数最少的多边形切割算法[10]将产生较长的切线和“窄长”(narrow)的矩形,窄长矩形在进行后续的颜色分配工作时会导致产生更多的冲突,并且窄长矩形往往也是薄片,如图5(a)圈中所示;而图5(b)本文算法虽然产生更多数目的矩形,但是消除了窄长矩形(薄片)的产生,大大减短了切线长度,从而减少冲突数目.
如图6的例子所示,图6(a)分解后矩形总数最少的多边形覆盖算法大多数允许分解后有交叠部分的矩形之间互相“穿透”(piercing)[9],不仅产生较长的切线总长度,并且由于交叠部分太大,产生的矩形尺寸很大,在进行颜色分配时会产生更多的冲突,更为重要的是,当交叠部分太大时,将原版图划分为2个子版图并没有有效地增加图形间距和降低版图密度,显然不适用于双成像光刻技术;而图6(b)本文算法分解后切线总长度较短,并且大大减少了分解后图形间交叠部分的面积,从而减少冲突数目,更适用于双成像光刻.
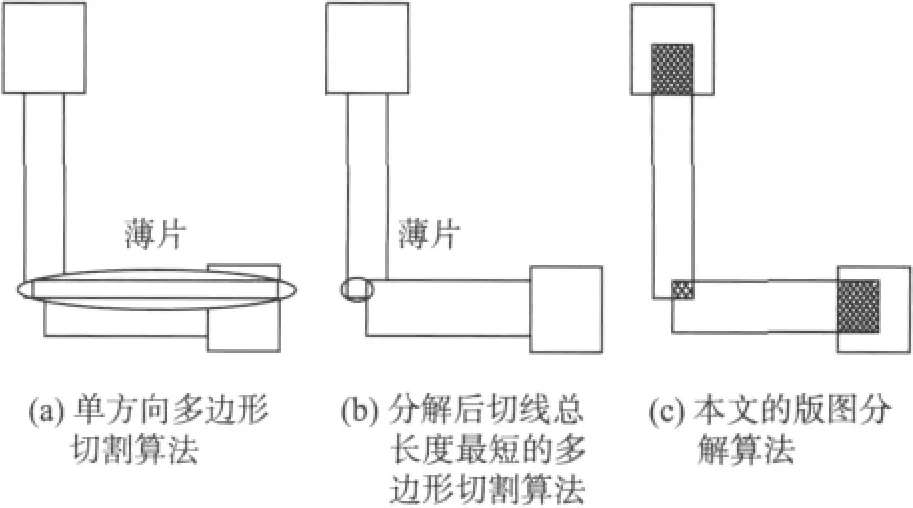
图4 对1个多边形的分解(Ⅰ)Fig.4 Fracture of a polygon(Ⅰ)
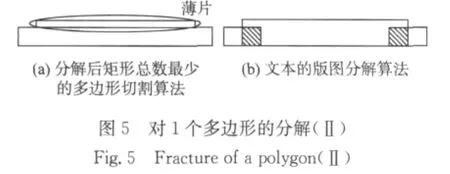

图7是使用本文算法和另2种现有算法对同1个多边形进行分解的情况.图7(a)是文献[15]提出的不允许交叠的矩形之间互相穿透的多边形覆盖算法,以分解后矩形总数最少为目标,可以看作是在覆盖算法和切割算法之间的折中.但是在这个例子中可见,即使不允许穿透,它依然产生较长的切线总长度和较大尺寸的矩形,将会增加颜色分配时的冲突数目,交叠部分尺寸也依然很大;为了
在分解时不产生薄片,图7(b)显示的文献[12]提出的减少分解后薄片数目的多边形切割算法通过添加辅助线(auxiliary ray)帮助分解,也因此产生较多数目的矩形和较长的切线总长度;图7(c)中的本文算法引入交叠,因而可以在切线总长度较短的地方进行分解而不产生薄片,如图7(c)圈中所示,同时产生较少的矩形,从而减少冲突数目和版图制造成本.
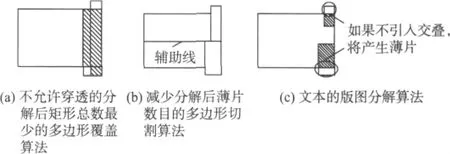
图7 对1个多边形的分解(Ⅳ)Fig.7 Fracture of a polygon(Ⅳ)
综合上述比较可知,现有的版图分解算法应用在双成像光刻时将产生的问题是:切割算法在光刻时都会由于覆盖误差而发生图形断开;其中单方向多边形切割算法会产生薄片,并且会产生较多数目的矩形和较长的切线,增加冲突数目和版图制造成本;分解后矩形总数最少的多边形切割算法会产生薄片,并且在一些情况下会产生较长的切线和窄长的矩形,增加冲突数目;分解后切线总长度最短的多边形切割算法会产生薄片,并且在一些情况下产生较多数目的矩形,增加冲突数目和版图制造成本;分解后矩形总数最少的多边形覆盖算法在一些情况下会产生较长的切线和较大尺寸的矩形,增加冲突数目,较大的交叠部分也降低了双成像光刻的有效性.因此,它们都不适用于双成像光刻.本文算法消除了薄片的产生,解决光刻时由于覆盖误差引起的图形断开问题,在减短切线长度的同时减少矩形数目,从而减少冲突总数和版图制造成本.
2 算 法
本文的版图分解算法能够对版图中的直角多边形和带斜角多边形进行分解.由于版图中的图形基本是简单多边形(simple polygon),本文算法也仅考虑简单多边形.版图中的直角多边形的所有边都是与坐标轴平行的直边,所有内角都是直角(90°或270°);带斜角多边形和直角多边形相比,包含了部分斜边和斜角,斜边即与坐标轴不平行的边.其中,根据版图中图形的特点,对本文考虑的带斜角多边形的形状提出以下2个限制:
1)2条斜边不相邻,即每条斜边的相邻边都是直边;2)斜角不包括锐角,即斜角都是钝角或优角.
图8显示了带斜角多边形中被这2个限制所排除的情况:2条斜边相邻,或斜角是锐角.图中使用顶点和与之相连的边表示带斜角多边形的一部分.在边一侧的阴影表明位于多边形内部.边使用有向线段表示,因为本文算法假定多边形在分解前已经经过一种预处理,使得遍历代表多边形的顶点点集时,所得到的有向闭环是逆时针方向.在本文接下来的部分中将多次使用类似图8的表示方法.
本文的版图分解算法将直角多边形分解为矩形,将带斜角多边形分解为矩形或所有内角都是直角或钝角的多边形.由于在本文算法中,直角多边形可以看作带斜角多边形的特例,所以接下来将主要针对带斜角多边形介绍算法,对直角多边形使用相同的算法处理.
在带斜角多边形中,所有内角都是钝角、90°直角或优角.显然地,需要在优角位置处进行分解.本文算法所使用的名词定义如图9所示.当前需要分解的优角称为当前优角,记作a,a的顶点称为当前点,记作N.在当前优角a(当前点N)处进行分解时,需要寻找多边形中的另1条边来参考产生切线,将所找到的这条边称为参考边(reference segment),记作r.如果把当前点N作为原点,使用版图的坐标方向建立1个直角坐标系,优角a的2条边不可能位于的区域是1个象限加上坐标轴的2个半轴,把表示这个区域的点集称为参考域(reference domain)(不包括当前点N),记作D.在图9中参考域D即第一象限加上x轴和y轴的正半轴,用以2条射线为边界的阴影表示,和边一侧表示多边形内部区域的阴影含义不同.为了与表示多边形的边的直线段相区别,将两条射线用虚线表示.本文算法所提到的边和线,在涉及集合运算时都视为包含其上所有点的点集.在本文算法中,限定所找到的参考边和所作的切线都只能是与坐标轴平行的直边(线).
根据参考域D所包含的象限不同,可以把优角a的位置分为4种情况.由于本文算法中对这4种情况下的分解过程极其相似,所以下文仅针对参考域D包含第一象限的情况,即如图9所示的情况进行描述,其他3种情况的分解可以通过类比得到.分解的基本原理是在优角位置处产生切线,将其分解为2个角,相应地将当前的多边形分解为2个多边形.由于切线只能是与坐标轴平行的直线,而优角的2条边里必有1条是直边,因此每次分解相当于使优角减去90°或180°,直至将所有优角都分解为钝角、90°直角、平角的组合时,分解完毕.根据优角a的角度范围,可以将优角a的形状分为3种情况:180°<a<270°,a=270°,270°<a<360°,如图10所示.其中(a),(c)只显示了优角a有1条水平方向的直边的情况,省略了有1条竖直方向直边的情况.

图8 在带斜角多边形中被2个限制所排除的情况Fig.8 Conditions excluded by two limitations in polygons with slant angles
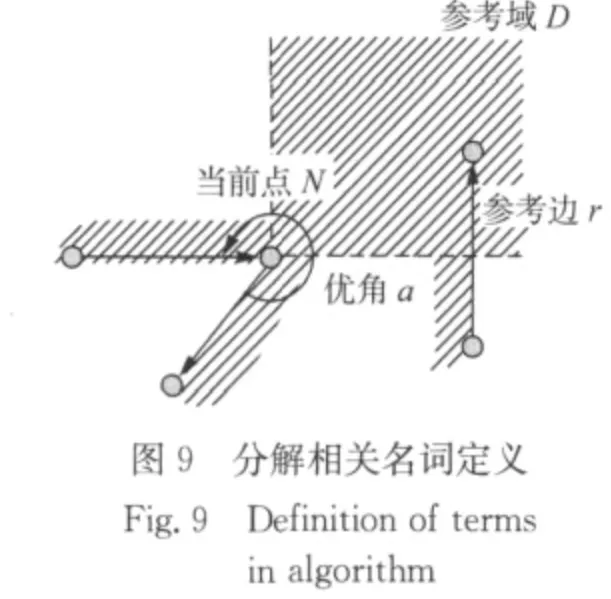

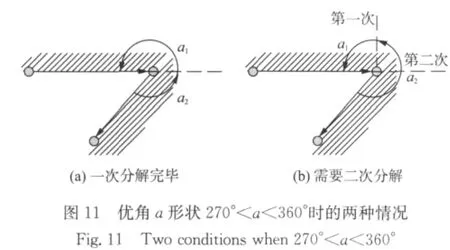
图10的优角a形状的3种情况中,图10(a)由于带斜角多边形形状限制2),切线只能是竖直方向(如果a有1条竖直方向直边,则切线只能是水平方向),分解后a=a1+a2,其中a1=90°,90°<a2<180°,1次分解完毕;图10(b)切线可以是竖直方向或水平方向,分解后a=a1+a2,其中a1=90°,a2=180°,也是1次分解完毕;图10(c)在分解时则又会出现2种情况,见图11.在图11(a)中,切线为水平方向,分解后a=a1+a2,其中a1=180°,90°<a2<180°,1次分解完毕;图11(b)中,切线为竖直方向,分解后a=a1+a2,其中a1=90°,180°<a2<270°,a2仍是优角,需要继续对a2进行分解,即对原优角a进行第二次分解.在下文中可知,由于在当前优角a和参考边r位置关系的7种情况中大多数都将引入交叠,在当前优角a满足270°<a<360°时,在进行1次分解后往往产生的2个多边形中有1个仍旧存在优角,需要进行第二次分解,类似图11(b)的情况.显然地,a有1条竖直方向直边的情况可以通过类比得到.
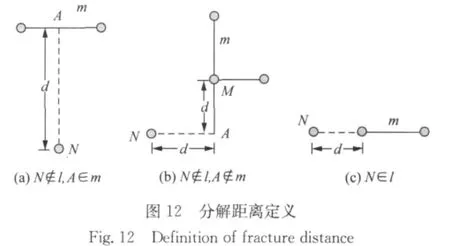
在优角a处产生切线时,需要在多边形中寻找参考边.记多边形中和参考域D有交集的直边的集合为R,多边形的边的集合记为P,则R={x|x∈P,x是直边且x∩D≠∅}.对集合R中的每一条边m,考察当前点N和边m之间的分解距离(fracture distance),记作d或d(N,m).如图12所示,分解距离定义如下:
记边m所在直线为l,如果N∉l,由当前点N向边l作垂线,交于垂点A.
1)如果A∈m,垂点A在边m内,则当前点N和边m的分解距离d(N,m)为点N和点A之间的距离,即点N和点A的纵坐标或横坐标的差的绝对值,d(N,m)=dy=|yN-yA|或d(N,m)=dx=|xN-xA|.
2)如果A∉m,垂点A在边m外,记M为边m的两个顶点中离垂点A距离较近的那个顶点,当前点N和边m的分解距离d(N,m)为点N和点M之间横坐标之差的绝对值和纵坐标之差的绝对值中的较大值,d(N,m)=max(dx,dy)=max(|xN-xM|,|yN-yM|).
如果N∈l,当前点N在边m所在直线内,记M为边m的两个顶点中离当前点N距离较近的那个顶点,当前点N和边m的分解距离d(N,m)为点N和点M之间的距离,(c)中即点N和点M的纵坐标或横坐标的差的绝对值,d(N,m)=dy=|yN-yM|或d(N,m)=dx=|xN-xM|.
选取集合R中和当前点N分解距离最短的边为参考边r,即r满足∀m∈R,d(N,r)=min(d(N,m)),其中r∈R.然后根据当前优角a和参考边r的位置关系进行分解.根据版图中图形特点和本文算法的名词定义,可以将当前优角a和参考边r的所有可能的位置关系归纳为7种情况.图13针对参考域D包含第一象限、当前优角a有1条水平方向的直边且270°<a<360°显示了当前优角a和参考边r位置关系的7种情况.为方便显示,图13中当前优角a未具体标明,可以通过当前点N和标明了多边形内部区域的a的两条边得到.同前文一致,虚线表示切线,阴影表示分解后图形间的交叠部分.因为在每次分解时,都确保若遍历这1次分解后所产生的2个多边形的点集,所得到的有向闭环也是逆时针方向,所以使用有向线段表示切线,这将帮助解释在优角位置处的分解是如何产生2个多边形的.为简单起见,和原多边形中的顶点相区别,图13中因产生切线而新增的顶点未具体标明.特别地,如果满足参考边定义的边r有多条,只需选取其中1条.图13(c)~(g)中,当前优角a需要和参考边r及其邻边所组成的另一个优角一起进行分解.另一个优角的2条边都被标明r,表示这两条边中任一条直边都可以被选为参考边.
在图13除去(e)以外的所有情况中,首先在当前点N和参考边r之间根据图12(a),(b)所示的分解距离的概念作出相应的切线,称为主切线.主切线将原多边形在当前优角处切割为2个多边形.然后,将其中1个多边形在主切线处增加1个以主切线为1条边的正方形部分,相应地增加切线,使两个多边形之间产生交叠.为不破坏原图形形状,正方形只在当前优角的参考域D内产生.在图13(b),图13(d),图13(f),图13(g)中,当前优角需要和另一个优角一起分解,要求这个正方形也必须在那个优角的参考域D′内.其中在图13(b),图13(d)中能够作出同时满足这2个要求的正方形,因此正常引入交叠;而在图13(f),图13(g)中无法作出这样的正方形,因此不引入交叠.在图13(e)中,同样根据图12(c)所示作出计算分解距离时所需要的边.因为有两种不同的作法,所以将得到四条切线.这四条切线本身就在引入交叠的条件下一起分解了当前优角和由参考边及其邻边所组成的另一个优角,不需要作额外的切线产生交叠.
在当前优角和参考边r位置关系的7种情况下的具体分解方法,体现本文算法所具备的优势是:
1)薄片是版图分解后所产生的宽度小于工艺尺寸的图形.对于版图中主要的直角多边形,考察图13(a)所示情况.在当前270°角处分解产生的两个多边形中,显然地,根据参考边的定义,上方不包含增加的交叠正方形的那个多边形的宽度必然不小于交叠正方形的边长,而由分解距离定义可知,交叠正方形的边长不小于版图工艺尺寸,因此上方多边形不是薄片.类似地,下方包含交叠正方形部分的多边形的宽度也大于交叠正方形边长,因此也不是薄片.图7(b)是包含图13(a)情况的一个具体例子,由图7可见如果不引入交叠或如文献[12]添加辅助线进行切割,必然会产生薄片,而按照本文算法增加一个正方形交叠部分,会消除薄片的产生.图13(b)~(d)情况类似.在图13(e)情况中,同样因为分解后的两个多边形均包含交叠正方形,因此都不是薄片,分解后消除薄片的产生.在图13(f),图13(g)情况中,因为无法引入交叠,因此会产生薄片,但是因为在版图的多边形中存在的比例极低,对本文算法的应用造成的影响极小.对于版图中少数的带斜角多边形,由于在寻找参考边时未考虑斜边,因此在图13所有情况中,切线都有可能会与多边形中的斜边(不包括当前优角和一起分解的另一个优角中的斜边)相交从而改变原多边形形状.如果要解决这个问题,可以通过在产生切线前对切线和多边形中的斜边进行关系检测(相应地增加算法时间复杂度),如果在图13(a)~(d)情况中被检测出发生相交的是除去主切线外的其他切线,则修改交叠部分大小,使分解后不改变原多边形形状;如果被检测出发生相交的是图13(a)~(d)情况中的主切线或图13(e)~(g)情况中的切线,则不进行分解.由于带斜角多边形在版图中比例很小,因此这个问题对本文算法的应用造成的影响也很小.并且,通过下文的实验可知,使用本文算法对带斜角多边形进行分解时,对原图形进行的这种改变往往也有利于提高原图形在光刻后的准确性.
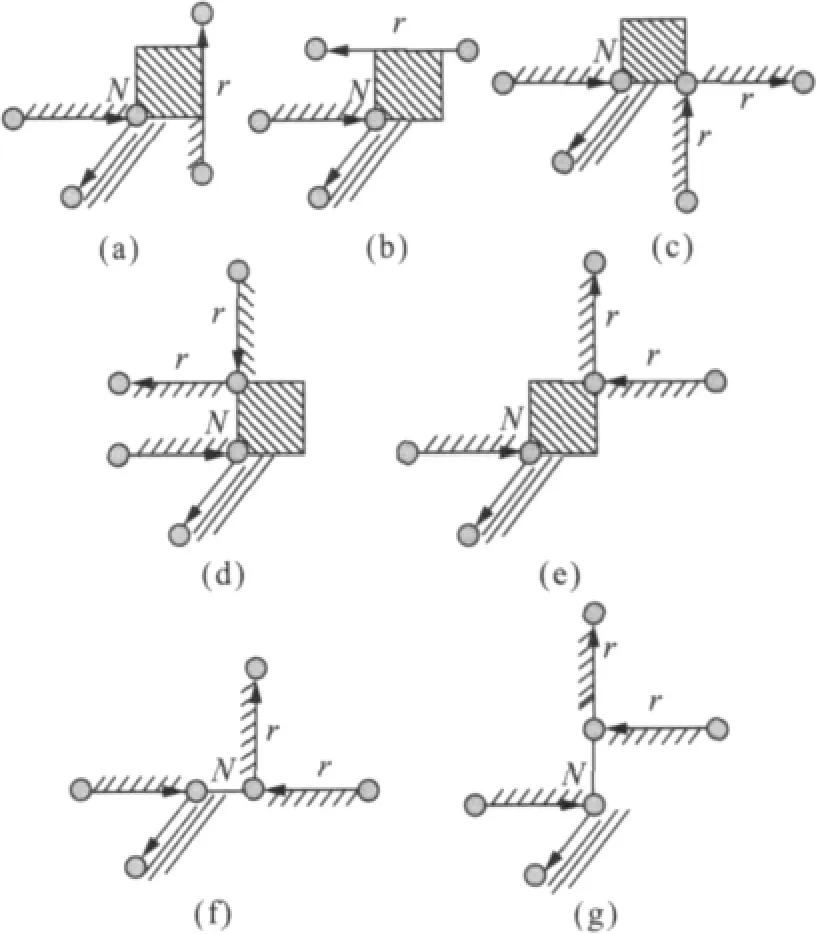
图13 当前优角和参考边r位置关系的七种情况Fig.13 Seven conditions of location relationship between current reflex angle and reference segment r
2)分解时,在当前优角和参考边r位置关系7种情况中的五种中引入交叠,交叠部分是边长为此最短分解距离的正方形.因为交叠正方形的边长不小于版图工艺尺寸,因此分解后的图形间的交叠部分足够大,在光刻时因覆盖误差引起图形尺寸和位置变化时能够保持原图形的完整性,解决图形断开问题.另外2种情况图13(f)和图13(g)中虽然分解时不引入交叠,但是在版图的多边形中存在的比例极低,对本文算法的应用造成的影响极小.
3)在所考察的集合中选取和当前点N分解距离最短的边为参考边r,并作出长度为此最短分解距离的切线进行分解,通过减少分解后切线总长度,使交叠部分足够小,从而减少冲突总数,提高双成像光刻的有效性.
4)由于版图中的图形大多数是直角多边形,当图13中的优角都是270°直角时,在除去图13(e)以外的6种情况中,是否引入交叠不影响分解后的矩形数目.在图13(e)情况中,多边形切割算法无法对这2个270°直角一起分解,因此分解后至少产生3个矩形,由图4可见;而本文算法引入交叠分解后产生2个矩形,减少分解后的矩形数目.在带斜角多边形中,当前优角a满足180°<a<270°时(见图10(a)),图13的7种情况都是1次分解完毕,分解后矩形数目和a=270°时相同,即和切割算法相同.当前优角a满足270°<a<360°时(见图10(c)),图13中除(f)外的6种情况都需要2次分解,将会增加分解后矩形数目.但是由于满足270°<a<360°的优角在版图的多边形中存在的比例极低,总体上,本文算法通过引入交叠,将减少分解后矩形数目,从而既能够减少冲突总数,又能够简化版图.
本文版图分解算法的流程表示如下:
输入:经过预处理的代表多边形的顶点点集V.
输出:代表分解后的图形的集合的顶点点集V和Vadd.
步骤1:遍历V中每个顶点;
步骤2:如果找到1个优角a(及当前点N);
步骤3:对于当前优角a,遍历V获取集合R,并从R中找到参考边r;
步骤4:根据当前优角a和参考边r位置关系情况进行分解;
步骤5:如果分解后产生的多边形在当前点N处的内角是优角,则继续分解;
步骤6:回到步骤1继续遍历.
3 实验结果及分析
本文的版图分解算法已用C++语言在Linux平台下实现.多边形由单链表数据结构实现.所有的实验结果都是在Linux平台下的Dell 2600PC机上运行得出的,Dell 2600PC机具有3.0GHz的XEON 3.0CPU和4GB内存空间.
本文算法的时间复杂度是O(n2).图14为1个实际的版图中多边形数目和单个多边形顶点数目的分布图.由图14中可见版图中绝大多数多边形的顶点数目小于18,因此在VLSI版图处理中本文算法的计算速度是可以接受的.
首先使用由直角多边形随机生成算法[16]生成的直角多边形例子和手工生成的带斜角多边形例子对本文算法的功能进行验证.通过输入大量的随机生成的顶点数不同的直角多边形例子和多个手工生成的带斜角多边形例子,结果显示程序都能正确分解.图15显示了程序对1个有1 000个顶点的直角多边形的分解结果.图15中分解后的图形使用带边框的多边形表示,分解后的图形间不交叠的部分显示为浅色,交叠的部分显示为深色,所有有色区域的包络即为原多边形形状.下文的实验结果也使用类似的表示方法.由图15可见程序正确地分解了复杂的直角多边形例子.

图14 版图中多边形数目±单个多边形顶点数目分布图Fig.14 Distribution of number of polygons-number of vertices per±polygon in layout
然后对实际版图的部分进行分解从而验证本文算法的功能.图16,图17分别为程序对1个22nm工艺版图的一部分和1个0.18μm工艺版图的一部分进行分解的结果.由图16可见本文算法能够对版图中的直角多边形进行正确地分解.在图17中,由于前文所述的原因,切线与多边形中的斜边相交,导致分解后的图形会有超出原多边形的部分,改变了原多边形的形状.但是,由于在光刻后,因为光学邻近效应(optical proximity effect,OPE)的影响,会发生拐角圆滑(corner rounding)现象,尖锐部分被“磨平”[13],即原多边形中的90°直角和钝角位置处在光刻后边界会内缩,因此在多边形中的90°直角和钝角位置处增加一些超出的部分将抵消光刻的失真影响,增加光刻的准确性.在图17中可见,对于版图中的斜角多边形,大部分情况下,本文算法分解后所得到的图形在超出原多边形的部分所在的位置处,原多边形的内角为钝角,将有利于版图光刻.并且大部分情况下超出部分足够小,不会对版图功能带来影响,如图中实线圈处所示,在少数情况下超出部分较大,对原多边形形状的改变将可能对版图功能产生影响,如图中虚线圈处所示,此时可以通过前文所述的对切线与斜边进行关系检测减少交叠部分来解决.

图15 程序对1 000个顶点的直角多边形分解结果Fig.15 Fracturing result of one rectilinear polygon with 1 000vertices
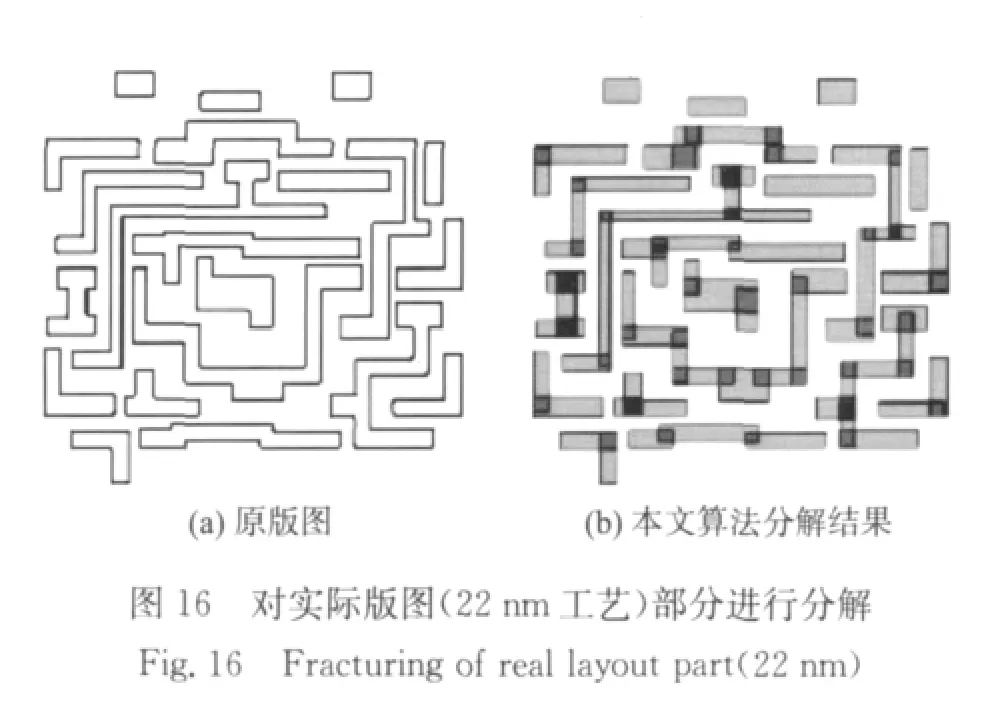
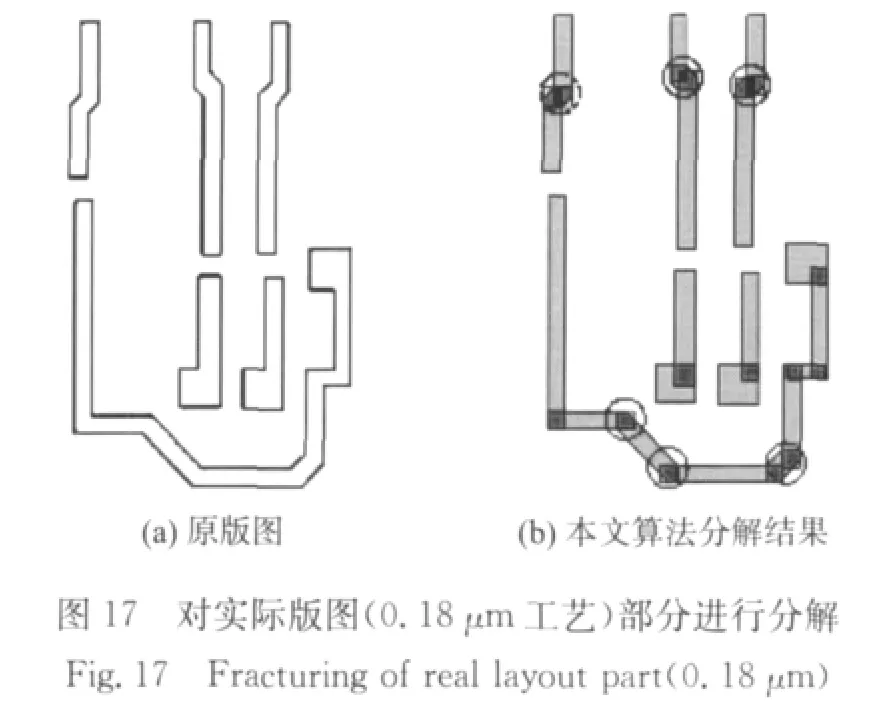
由图16和图17可见,本文算法在分解后不存在薄片,交叠部分被控制在足够小的区域,能够保证双成像光刻的性能.分解后相连的多边形间都存在交叠部分,能够解决由于覆盖误差引起的图形断开问题.图18是对图16(a)的版图部分进行版图分解和颜色分配后的结果[17],其中图18(a)是本文算法在不允许分解后图形间存在交叠的前提下的处理结果,图18(b)是本文算法的处理结果.由图中可见,当不引入交叠时,版图分解后的图形中会存在大量薄片,导致在颜色分配后子版图中仍旧存在薄片,如图18(a)中的圈中所示,将给光刻带来极大挑战;而本文算法分解时通过引入交叠完全消除薄片的产生,因此颜色分配后的子版图不存在薄片,可以安全地进行光刻.
图19显示了分别当图18的两种算法处理情况下的子版图间发生相同偏移产生覆盖误差时的情况.子版图间的偏移同时包括x方向和y方向.由图19(a)所示,由于不引入交叠,子版图间产生很小的偏移也会导致原版图图形发生多处断开,如图中圈中所示部分,多处断开将对版图功能产生很大影响;而图19(b)本文算法的情况下,由于引入了不小于版图工艺尺寸大小的交叠部分,在子版图发生偏移时能够维持版图图形的形状不发生断开,将能够有效地解决因覆盖误差导致的图形断开问题,降低覆盖误差对双成像光刻技术的影响.表1列出了对于两个实际的版图,使用不同的分解算法进行版图分解、颜色分配和图形合并后,薄片的数目.由表1可见,使用单方向分解算法时,将产生大量薄片;不引入交叠的算法(在不允许交叠的前提下的本文算法)也会产生接近原版图多边形1%比例数目的薄片;而本文算法消除了薄片的产生,避免产生光刻工艺无法接受的版图,适用于双成像光刻技术.
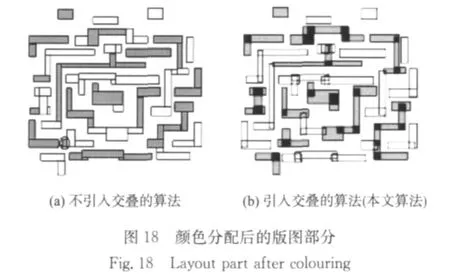
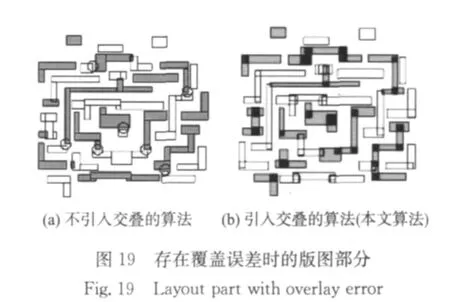

表1 不同分解算法处理后薄片的数目Tab.1 Number of slivers by different algorithms
本文提出一种新的版图分解算法,应用于双成像光刻技术,将版图中的直角多边形和带斜角多边形分解为矩形和所有内角都是90°直角和钝角的多边形,以实现分解后的图形不存在薄片为前提,以减少颜色分配后的冲突总数为目标,主要通过在可接受的时间复杂度下减少分解后切线总长度,同时引入交叠.引入交叠消除薄片的产生,同时解决由于覆盖误差引起的图形断开问题,并减少分解后的矩形数目,不仅减少冲突总数,也简化版图降低制造成本.通过实验验证该算法正确实现了上述功能,比现有算法更适合用于双成像光刻技术.
[1]ALICE.EUV与18英寸晶圆工艺皆延迟,业界焦急与无奈[EB/OL].电子工程专辑.(2012-02-16)[2012-03-07].http:∥www.eet-china.com/ART_8800661433_480201_NT_be26a1ef.HTM.
[2]International Technology Roadmap for Semiconductors 2011Edition [R/OL].(2012-03-07)[2012-04-07].http:∥www.itrs.net/Links/2011ITRS/Home2011.htm.
[3]Dusa M,Finders J,Hsu S.Double patterning lithography:The bridge between low k1ArF and EUV[J].MicrolithographyWorld,2008,17(1):2-7.
[4]Mack C.Seeing double[J].Spectrum,IEEE,2008,45(11):46-51.
[5]Kahng A B,Park C H,Xu X,etal.Layout decomposition approaches for double patterning lithography[J].IEEETransactionsonComputer-aidedDesignofIntegratedCircuitsandSystems,2010,29(6):939-952.
[6]Yuan K,Yang J S,Pan D Z.Double patterning layout decomposition for simultaneous conflict and stitch minimization[J].IEEETransactionsonComputer-aidedDesignofIntegratedCircuitsandSystems,2010,29(2):185-195.
[7]黄惠萍,陆伟成,付 强,等.基于延迟合并嵌入的带障碍的时钟树布线算法[J].计算机辅助设计与图形学报,2008,20(6):718-723.
[8]Lingas A,Pinter R,Rivest R,etal.Minimum edge length partitioning of rectilinear polygons[C]∥Proceedings of the 20th Annual Allerton Conference on Communication,Control,and Computing.Illinois,America:Allerton Retreaat Center,1982:53-63.
[9]Wu S Y,Sahni S.Covering rectilinear polygons by rectangles[J].IEEETransactionsonComputer-aided DesignofIntegratedCircuitsandSystems,1990,9(4):377-388.
[10]Wu S Y,Sahni S.Fast algorithms to partition simple rectilinear polygons[J].VLSIDesign,1994,1(3):193-215.
[11]Gourley K D,Green D M.A polygon-to-rectangle conversion algorithm[J].IEEEComputerGraphics andApplications,1983,3(1):31-36.
[12]Kahng A B,Xu X,Zelikovsky A.Fast yield driven fracture for variable shaped beam mask writing[C]∥Photomask and Next-Generation Lithography Mask Technology XI.SPIE-The International Society for Optics and Photonics.Yokohama,Japan:2006:62832R.
[13]Sezginer A.Challenges in double patterning EB/OL.(2007-02-26)[2011-04-18].http:∥electronics.wesrch.com/paper-details/pdf-EL1SE14BIX144-challenges-in-double-patterning-by-apo-sezginer-cto-invarium.
[14]Wiaux V,Verhaegen S,Cheng S,etal.Split and design guidelines for double patterning[C]∥Optical Microlithography XXI.SPIE-The International Society for Optical Engineering.San Jose,CA,USA:2008:692409.
[15]Keil J M.Covering orthogonal polygons with non-piercing rectangles[J].InternationalJournalof ComputationalGeometryandApplications,1996,7(5):473-484.
[16]沈 聪,陆伟成,魏晗一.基于解开操作的直角多边形随机生成算法[J].计算机工程,2011,37(6):269-271.
[17]Luk W S,Huang H P.Fast and lossless graph division method for layout decomposition using SPQR-tree[C].Proceedings of the International Conference on Computer-Aided Design.Piscataway,N J,USA:IEEE press,2010:112-115.

