基于TIGGE多模式集合的24小时气温BMA概率预报

刘建国 谢正辉 赵琳娜 贾炳浩

1 中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京 100029

2 中国科学院大学，北京 100049

3 中国气象局公共气象服务中心，北京 100081

1 引言

为了减少大气系统预报的不确定性，数值天气预报已经由单一值的确定性预报进入到集合预报时代（Gneiting and Raftery, 2005）。多模式集合预报着眼于捕捉包括初边界条件以及物理过程的不确定性以期提高预报技巧，已成为多家数值天气与气候预报中心进行天气、气候预测的基础平台（Molteni et al., 1996; Grimitt and Mass, 2002; 陈静和陈德辉, 2002; Barnston et al., 2003; Palmer et al.,2004）。充分展示集合预报的潜力需要对模式输出进行统计后处理，并通过率定去除单个模式偏差、提高预报与观测的相关性来提高预报精度。对某一时间和地点的多模式集合预报是从概率密度函数（probability density function, PDF）取样，该PDF描述了集合预报的不确定性，给出天气变量的概率预报且量化相关天气风险，比确定性预报具有更大的经济价值，并广泛应用于电力、航空、气象导航、天气风险金融、疾病模拟等（Palmer et al., 2004; 杜钧和陈静, 2010; 赵琳娜等, 2010）。

早期概率预报大都是基于线性回归方法（Glahn et al., 1972; Bermowitz, 1975）或Logistic回归方法（Applequist et al., 2002; Hamill et al.,2004），它们只给出超过某个阈值的特定事件发生概率而不能给出全部预报的PDF。近年来，一些能够充分利用集合预报全部信息并获得完整 PDF的概率预报方法研究也已取得进展，如分层模型方法（Krzysztofowicz and Maranzano, 2006）、可靠性集合平均方法（Smith et al., 2009）、贝叶斯模型平均方法（Bayesian model averaging, BMA）（Raftery et al., 2005）。BMA能产生率定的、高集中度的预报PDF，它对某一特定变量的概率预报（PDF）是经过偏差校正的单个模型概率预报的加权平均，其权重是相应模型的后验概率，代表着每个模型在模型训练阶段相对的预报技巧。应用研究表明基于BMA方法进行集合预报具有优势（Wilson et al., 2007;Duan et al., 2007; Sloughter et al., 2007, 2010; 杨赤等, 2009; Fraley et al., 2010）。

BMA方法最初应用于集合预报系统中服从Gaussian分布的地面气温和海平面气压等天气变量（如 Raftery et al., 2005; Wilson et al., 2007），以及后来应用于不服从Gaussian分布的降水和风速等天气变量（Sloughter et al., 2007, 2010)。Fraley et al.(2010) 进一步将BMA方法应用于集合预报成员具有可替换性和缺失的情况。这些研究主要是对欧美一些典型区域进行多模式集合的BMA概率天气预报试验，缺乏针对中国区域基于多模式集合 BMA概率预报的率定、评估及充分发展概率预报潜力的研究。淮河流域水文气象特点复杂，极端事件频发，是水文气象研究的典型流域。而 TIGGE（The THORPEX Interactive Grand Global Ensemble）收集了全球多个气象业务中心的全球中期业务集合预报系统的多成员、多要素、多时效的预报结果，为评估多模式集合预报系统和概率性预报及其拓展应用提供了很好的支持。本文以淮河流域为研究区域，利用 TIGGE四个中心 European Centre for Medium-Range Weather Forecasts (ECMWF)、United Kingdom Meteorological Office (UKMO)、China Meteorological Administration (CMA) 和 United States National Center for Environmental Prediction(NCEP) 的2007年6月1日至2007年8月31日夏季三个月的 24小时地面日均气温集合预报结果，结合研究区域内 43个站点观测，通过率定不同中心及多中心超级集合的BMA模型参数，建立针对流域内各站点的BMA概率预报模型，改进了地面气温的预报技巧。并对BMA概率预报效果进行评估，探讨各中心及超级集合预报产品在研究区域的适应性。利用已建立的BMA概率预报模型做出地面日均气温的百分位预报，提出基于百分位预报的高温预警方案，展示了多中心模式超级集合预报产品及概率预报的应用潜力。

下面第二节介绍BMA方法的基本理论框架，第三节是研究区域与数据，第四节是试验结果及分析，最后一节是小结和讨论。

2 贝叶斯模型平均（BMA）

2.1 BMA模型

BMA是一种结合多个统计模型进行联合推断和预测的统计后处理方法，Raftery et al.(2005) 将其推广应用到多个动力模型中。令 f=f1,…,fK分别表示K个不同数值模式的预报结果，y代表需要预报的变量，yT代表培训数据。BMA预报模型（BMA预报 PDF）可表示为如下的多模式概率预报加权平均的形式：

这里 pk(y|(fk,yT))是与单个集合成员预报 fk相联系的条件概率密度函数，可解释为预报变量y在模型训练阶段模式预报fk为最佳预报条件下的概率密度函数，表明 fk在模型训练阶段为最优预报的可能性；wk表示在模型训练阶段第k个成员预报为最佳预报的后验概率，非负且满足，反映的是每个模型成员在模型训练阶段对预报技巧的相对贡献程度。当预报变量服从正态分布，如地面气温和海平面气压等，pk(y|(fk,yT))为正态分布密度函数，其预报变量均值或期望为原始预报结果的简单线性函数ak+ bkfk，标准偏差为σ，即：

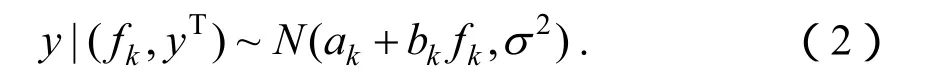
由此及（1）可知BMA预报均值为也即BMA模型的确定性预报结果。若令s，t分别表示空间与时间指标，kstf表示预报集合中第k个成员在空间s与时间t的预报结果，则公式（1）相应BMA预报方差为

BMA预报方差（4）包含两项：第一项表示预报集合的离散程度，第二项表示集合内的预报方差。

2.2 BMA模型参数的率定

BMA预报模型参数包括ak, bk,wk(k=1, 2, …,K) 与σ2。它们的率定参照Raftery et al.(2005) 提出的方法，利用一套培训数据，ak, bk(k=1, 2, …, K)通过线性回归

来确定，而wk(k =1, 2, …, K)与σ2通过极大似然原则来率定。假定预报误差在空间s与时间t上相互独立，则对数似然函数为

方程（6）不存在解析的极大值解，需要进行迭代求解。Raftery et al.（2005）提出在预报变量服从正态分布的情形下使用 Expectation-Maximization（EM）算法求解，Vrugt et al.（2008）提出适应一般情形的Markov chain Monte Carlo（MCMC）方法，能获得全局最优解，但计算量较大，田向军等（2011）提出了使用一种有限记忆拟牛顿优化算法求解，并比较了三种算法的优缺点。实际操作中迭代算法的选取取决于预报变量的类型以及计算量的大小。EM 算法虽只能获得局部最优解，但算法简单，易于编程实现，计算速度快，对于服从正态分布的预报变量更加有效可行。气温服从正态分布，因此本研究在BMA方法中选择Raftery et al.（2005）采用的 EM 迭代算法求解方程（6）从而获得参数 wk(k =1, 2, …, K)与σ2。这里引入一个非观测变量 zk,s,t，求解方程（6）的具体EM迭代算法如下：

1）初始化：让

n是培训期观测数据总和；

2）计算初始对数似然函数：

3）Expectation（E）步：将j替换为j+1，对所有的k, s, t，计算

4）Maximization（M）步：计算权重

更新方差

2.3 具有可替换集合成员的BMA模型

对于集合预报中的一些在统计上不易区别的集合成员，比如仅仅是由于随机扰动形成的不同集合成员，像TIGGE中每个业务中心的扰动预报成员，我们可认为其为可替换的集合成员。对于可替换的集合成员我们可以考虑他们具有相同的 BMA权重和BMA参数，从而可以减少计算量。根据Fraley et al.(2010) 的研究，修改BMA方法应用于具有可替换集合成员的集合预报。假设将m个集合成员分成I组，每组有im个可替换集合成员，即让f,ij描述第i组第j个集合成员预报结果，y,ij为相应的校正结果，BMA预报模型（1）可写为

对于EM算法，E步（8）可写为

M步（9）～（10）可写为：

对集合预报结果进行BMA概率预报可归结为以下三步：1）确定培训期长度；2）采用EM算法及培训数据率定 BMA模型参数；3）获得相应的BMA模型。本文采用回归滚动预报方式，即培训期是一个滑动窗口，BMA采用先前的N天作为培训期进行训练，培训出的BMA系数应用到下一天（24小时预报）的BMA模型预报中，每一天动态建立研究区域内各站点的BMA模型。试验中验证期的每一天在研究区域内所有站点的BMA概率预报可以累积来验证预报技巧。

3 研究区域与数据

淮河是我国南北自然分界线，地处南北气候过渡带，流域内水文气象特点复杂，极端天气事件频发，本研究取淮河流域作为研究区域（图1）。

观测资料为Li and Yan (2009) 均一化处理更新的该区域内43个基准气象站2007年6月1日至8月31日地面日均气温观测。模式结果为同时期ECMWF、UKMO、CMA、NCEP四个TIGGE中心四套全球集合预报系统多集合成员的24小时地面日均气温集合预报结果。起报时间为世界时（格林威治时间）每日00时，各中心集合预报的集合成员数等有关信息可参见表1。根据ECMWF、NCEP、UKMO、CMA各成员输出的地面日均气温24小时集合预报结果，其均为0.5°×0.5°的格点数据，使用双线性插值方法获得流域内站点的集合预报结果。

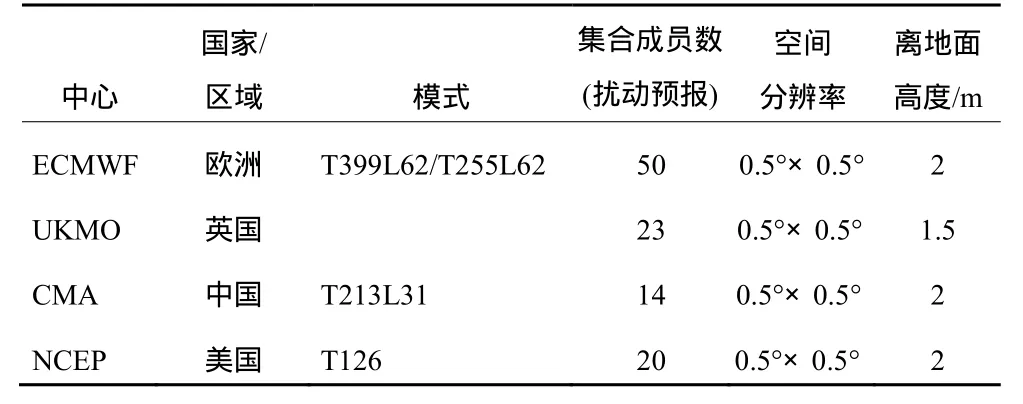
表1 本研究采用的TIGGE四个单中心集合预报系统（ECMWF、NCEP、UKMO、CMA）的比较Table 1 Comparison of four single–center ensemble prediction systems in TIGGE in this study (ECMWF,UKMO, CMA, NCEP)

图1 淮河流域及43个基准气象观测站Fig.1 Illustration of the Huaihe River basin and the location of 43 standard meteorological stations

4 结果

4.1 培训期长度

对不同时期、不同研究区域，BMA模型的培训期长度也不同。以一个中心一段时期的集合预报结果和观测作为培训数据，使用不同的培训期长度来建立 BMA概率预报模型，通过平均绝对误差（mean absolute error, MAE）、90%预测区间宽度、连续等级概率评分（continuous ranked probability score, CRPS）（Gneiting and Raftery, 2007）三种指标检验BMA模型性能，确定培训期长度。平均绝对误差用来检验确定性预报精确度，这里原始集合预报的确定性预报是指其均值。90%预测区间宽度和连续等级概率评分用来检验概率预报的精确度和集中度。三种指标都是负导向的，值越小模型性能即预报效果越好。

考虑UKMO中心10天、15天、20天、25天、30天、35天、40天、45天和50天九种培训期的BMA模型，选取7月21日至8月31日作为验证期，各项检验指标取验证期期间所有站点的均值。表2给出了BMA模型与原始集合预报各项检验指标均值，从表2中可看出不同训练期长度的BMA模型比原始集合预报所有的指标都要小，这说明BMA模型比原始集合预报的效果好。图2 给出了不同长度培训期的 BMA模型各项检验指标均值的比较，从图 2a中可以看出, 在30天以前随着培训期的天数增加，MAE在不断变小，30天以后就有较稳定的MAE；从图2b中可以看出，30天以后有较稳定的、较小的CRPS，且30天后的CRPS减少的幅度很小；从图2c中可以看出，在30天以前随着培训期的天数增加，90%预测区间宽度在增加，30天以后趋于稳定。综合考虑MAE、CRPS、90%预测分布区间宽度三个指标以及计算量，培训期为30天时趋于稳定并得到较优的预报效果，因此选择培训期为30天。

表2 不同长度培训期BMA模型和原始集合预报（Ens）的检验指标均值Table 2 Verification metric mean of BMA predictive models and raw ensemble forecasts (Ens) of average daily surface air temperature for different training period lengths

4.2 单中心集合的BMA概率预报

4.2.1 BMA概率预报实例

对于BMA概率预报，首先描述单个预报变量在一个站点一天的BMA预报PDF实例，后面将给出多站点多时间的模型性能结果。图3给出了一个BMA概率预报实例：UKMO中心 54945站 2007年8月1日地面日均气温的BMA概率预报PDF。图3中BMA预报PDF的主要成分是指主要成员（BMA模型中占主要权重的成员）预报PDF与相应权重的乘积。

4.2.2 模型比较与检验评估

考虑不同中心BMA概率预报PDF，通过平均绝对误差、90%预测区间宽度、连续等级概率评分三种指标检验和评估 TIGGE四个中心集合预报产品BMA概率预报效果，选取7月1日至8月31日作为验证期，各项检验指标取验证期期间所有站点的均值。表3给出了四个中心BMA模型与原始集合预报的各项检验指标均值，从表3中可以看出各中心的集合预报产品的BMA概率预报模型都比原始集合预报效果好。图4给出了四个中心BMA模型各项检验指标均值的比较，可以看出，ECMWF具有较小的 MAE（图 4a）与 90%预测区间宽度（图 4c），ECMWF和UKMO有较小的CRPS（图4b）。综合考虑，ECMWF具有最好的预报效果，UKMO次之。

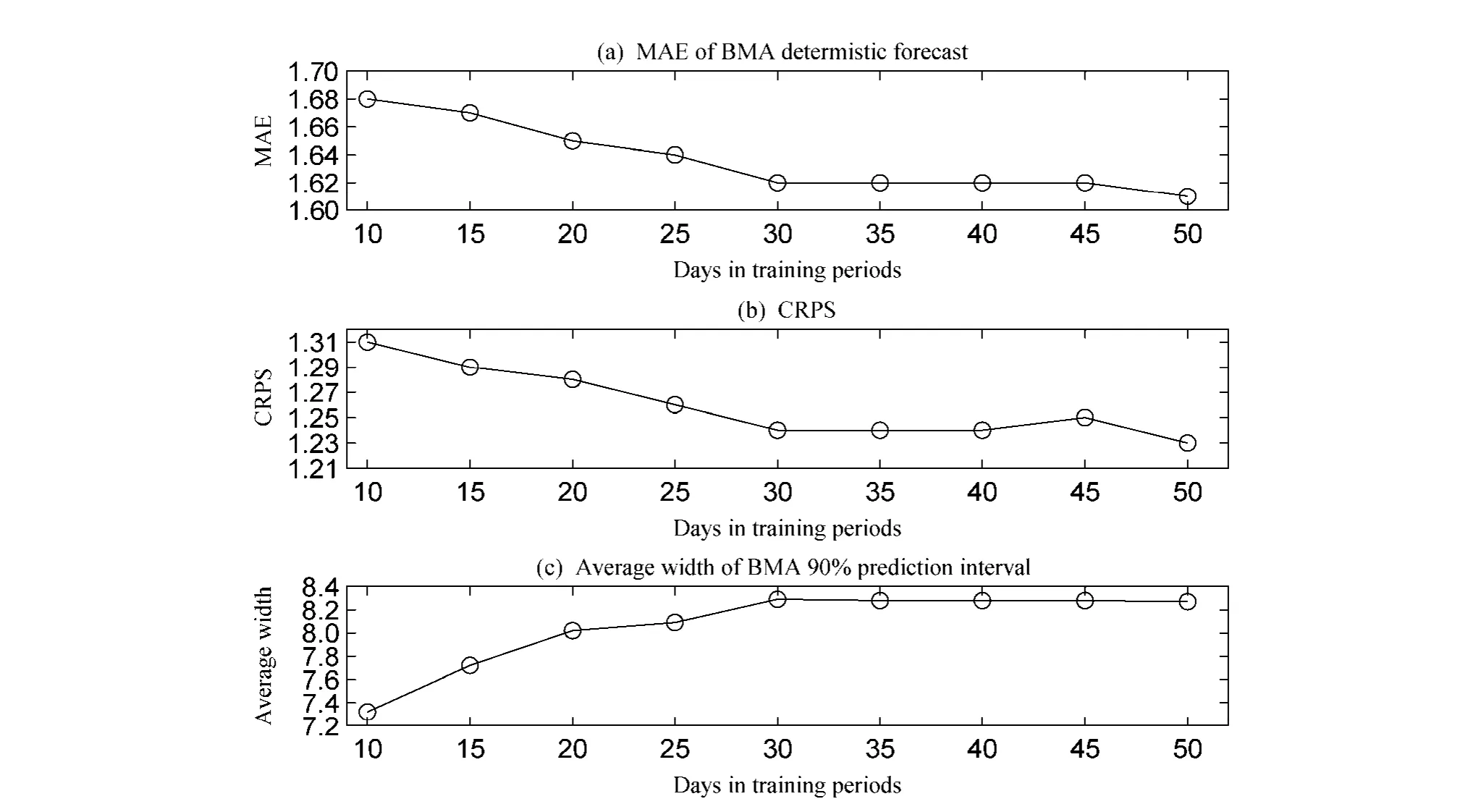
图2 不同长度培训期BMA模型性能检验指标均值比较：(a) BMA确定性预报的MAE; (b) CRPS; (c) BMA 90%预测区间宽度Fig.2 Comparison of BMA predictive models of average daily surface air temperature for different training period lengths: (a) MAE of BMA deterministic forecasts; (b) CRPS; (c) average width of 90% prediction interval

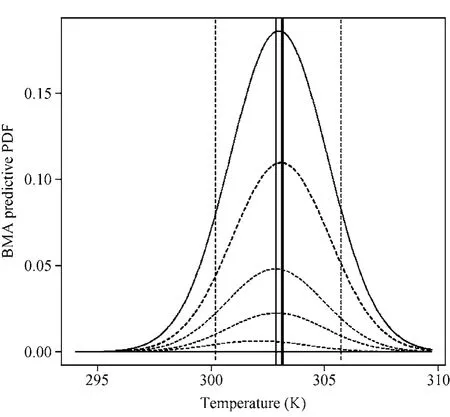
图3 UKMO中心54945站2007年8月1日地面日均气温BMA预报PDF。实曲线是BMA预报PDF，虚曲线是BMA预报PDF的主要成分，粗垂直实线是观测，细垂直实线是确定性预报，垂直虚线是BMA预报PDF 的第10百分位和第90百分位预报Fig.3 BMA predictive PDF of average daily surface air temperature from UKMO at station no.54945 on 1 Aug 2007.The upper solid curve is the BMA predictive PDF; the lower dashed curves are major components of BMA predictive PDF; the thick vertical line is verifying observation, the thin vertical line is the deterministic forecast; the dashed vertical lines indicate the 10th percentile and 90th percentile forecasts from the BMA predictive PDF

表3 TIGGE四个单中心集合预报系统BMA模型和原始集合预报（Ens）的检验指标均值Table 3 Verification metric mean of BMA predictive models and raw ensemble forecasts (Ens) of average daily surface air temperature for four single–center ensemble prediction systems

4.3 超级集合的BMA概率预报

4.3.1 模型比较与检验评估

图4 TIGGE单中心集合预报系统BMA模型性能检验指标比较：(a) BMA确定性预报的MAE；(b) CRPS；（c）BMA 90% 预测区间宽度Fig.4 Comparison of BMA predictive models of average daily surface air temperature for four single–center ensemble prediction systems: (a) MAE of BMA deterministic forecasts; (b) CRPS; (c) average width of 90% prediction interval

使用 TIGGE四个中心的扰动集合预报形成TIGGE多中心模式超级集合预报系统，共有107个成员。考虑到每个中心采用的是同一个模型形成的扰动集合预报，认为其集合成员为可替换成员，根据Fraley et al.（2010）的研究，对于可替换成员在BMA模型中可以给予他们等权重、同参数。本节应用考虑、不考虑（普通）可替换成员的BMA模型于TIGGE超级集合预报系统，选取7月1日至8月31日作为验证期，利用三种指标检验和评估各中心及多中心超级集合预报系统BMA模型预报效果，各项检验指标取验证期期间所有站点的均值。表 4是可替换原则下 BMA模型各中心成员的权重均值，从表4可以看出，ECMWF贡献了大部分的比例，50个成员均占0.0159，其他几个中心集合预报系统成员贡献较少，这也验证了前面试验ECMWF的集合预报系统有最佳的区域适应性的结论。表 5给出了单中心、多中心超级集合预报BMA模型与原始集合预报的检验指标均值，从表 5中可以看出，所有的BMA模型预报效果比原始集合预报好。图5给出了BMA模型检验指标均值比较，从图5可以看出超级集合（grand ensemble，GE）的普通BMA模型比单中心集合预报系统的BMA模型有更好的预报效果，考虑可替换原则的超级集合（grand ensemble considering exchangeable members, EGE）BMA模型大大减少计算量且在所有集合预报系统的BMA模型中有最好的预报效果，比原始集合预报在MAE上减少近7%，在CRPS上提高近10%。

4.3.2 百分位预报与极端事件分析

BMA概率预报模型给出的完全PDF包含了多中心模式集合预报不确定性的定量估计，从中可以分析出高温等极端天气事件信息。由上节的讨论，考虑可替换原则的超级集合BMA概率预报具有最佳预报效果，根据BMA预报PDF给出百分位预报，通过分析百分位预报个例，提出基于集合预报的概率分布来预警高温天气的方案，探讨如何捕捉PDF中极端事件信息，并讨论其局限性。

表4 考虑可替换原则的TIGGE超级集合BMA模型中各中心集合成员权重均值Table 4 Weight mean of BMA predictive models for TIGGE grand ensemble with exchangeable members

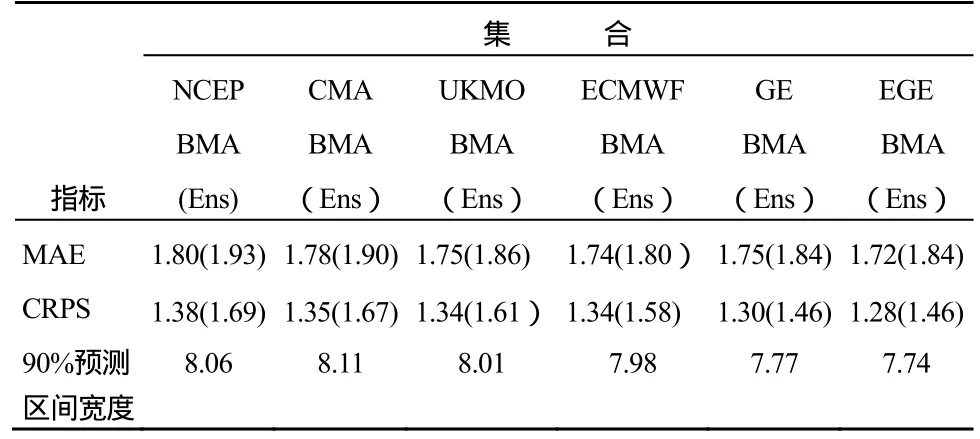
表5 集合预报系统BMA模型和原始集合预报（Ens）的检验指标均值Table 5 Verification matric mean of BMA predictive models and raw ensemble forecasts (Ens) of average daily surface air temperature for different ensemble prediction systems

图5 TIGGE单中心与超级集合预报系统BMA模型性能检验比较：(a) BMA确定性预报的MAE；(b) CRPS；(c) BMA 90%预测区间宽度Fig.5 Comparison of BMA predictive models of average daily surface air temperature for different ensemble prediction systems: (a) MAE of BMA deterministic forecasts; (b) CRPS; (c) average width of 90% prediction intervals

图6 淮河流域27个站点地面日均气温百分位预报与观测：（a）2007年7月26日；（b）2007年8月1日Fig.6 Percentile forecasts and observations of average daily surface air temperature at 27 stations in Huaihe River basin on (a) 26 Jul 2007 and (b) 1 Aug 2007

图6给出了2007年7月26日（图6a）、8月1日（图6b）两天淮河流域无缺失数据的27站点地面日均气温百分位预报。对于正常气温，BMA确定性预报能较好预报当天地面日均气温状况（图6a）；然而确定性预报对高温天气几乎没有预报能力（图6b）。图7给出了2007年7月9日至8月8日57290站的百分位预报，同样表明确定性预报能成功预报当月大部分日期的地面日均气温而不能预报高温天气。由此可知只有概率预报才有可能做出高温预警，7月11、17、18日与8月1日的四次高温天气中，每次观测温度都高于95百分位点，其中7月18日和8月1日这两次的95百分位点明显高于其他相同百分位点以及高温点（303.15K）（图7）。若从更多的历史集合预报和观测记录找到类似规律，则可提出该区域预警高温天气的方案：高温事件对应于概率预报的95百分位点，若95 百分位点已经高于高温点也明显高于其他相同百分位点，那么就应该进行高温预警，决策者也应该考虑采取应对高温的措施。图8给出了2007年7月9日至 8月 8日 54916站地面日均气温预报超过303.15K（30℃）高温天气的概率。从图 8可以看出预报的高温概率与观测气温表现出比较好的一致性，特别是这一个月的两次高温事件都能得到较好的预报，这从另一个角度说明根据概率预报进行高温预警的可行性。

图7 2007年7月9日至8月8日57290站地面日均气温百分位预报与观测Fig.7 Percentile forecasts and observations of average daily surface air temperature at station no.57290 from 9 Jul to 8 Aug, 2007

图8 2007年7月9日至8月8日54916站地面日均气温预报超过303.15 K高温的概率与观测Fig.8 Probability of exceeding 303.15 K and observations for average daily surface air temperature at station no.54916 from 9 Jul to 8 Aug, 2007

根据概率预报进行高温预警也有局限性，存在虚报、漏报等预报不准的风险，如图7和图8中7月21日都属于高温高概率预报，而事实上该天都属于夏天的正常温度，属于虚报。因此，如何从概率预报中捕捉到更多有用信息以减少虚报、漏报，增加概率预报对高温等极端天气事件预报的准确度，这既是对概率预报的挑战，也是今后努力的方向。

5 小结与讨论

将BMA方法应用于淮河流域进行地面日均气温概率预报试验，动态建立了流域内各站点 BMA概率预报模型，并对 TIGGE四个单中心及多中心模式超级集合预报系统在研究区域的预报技巧进行评估。通过BMA概率预报PDF，极大地提高了地面气温的预报技巧，展示了多中心模式超级集合产品及BMA概率预报的应用潜力，特别是在极端事件预报方面的潜力。BMA概率预报试验结果显示：研究区域的 TIGGE多模式集合的 BMA模型培训期长度选择 30天较为合适，且所有 BMA模型比原始集合预报有更好的预报效果；TIGGE各中心集合预报的 BMA模型都有较好的预报效果，ECMWF最优；普通的 TIGGE多中心模式超级集合BMA模型比单中心集合预报的BMA模型有更好的预报效果。采用可替换原则的多中心模式超级集合的 BMA模型，既能节省计算量又有最好的预报效果，它与原始集合预报相比，其MAE有近7%的减少，CRPS有近10%的提高；根据已建立的BMA预报PDF，给出了百分位预报，提出了基于集合预报的概率分布来预警高温天气的方案。

BMA概率预报能向用户提供完全的 PDF，该PDF定量描述了多模式集合预报的不确定性，通过分析研究BMA概率预报PDF，可以提高预报精度特别是极端事件的预报能力，但是任然存在对极端事件的漏报和误报。我们可以通过改进BMA方法和进一步探讨从BMA预报PDF中挖掘出更多有用信息来减少漏报和误报，提高预报精度。比如BMA方法中采用不同的偏差校正方法和参数率定方法对概率预报效果有一定的影响，特别是对像降水等其他非正态分布的天气预报变量（Schmeits and Kok,2010; 田向军等, 2011）。BMA方法中偏差校正方法以及参数率定方法的改进，BMA预报PDF中有用信息的挖掘，对于这些问题值得在今后的研究中进行深入探讨，以期获得更优的BMA概率预报效果。

BMA方法本质上是一个模型训练的统计方法，必须利用观测数据对模型集合中的各个预报模型进行训练，测试以确定其系数。在训练过程中对培训数据的选取非常重要，培训期的长度也具有区域性和时间性，需要不断试验以及经验，才能获得最佳的预报效果。由于该方法对观测资料的依赖性，使得其应用也具有一定的局限性。

致谢 感谢中国科学院大气物理研究所严中伟研究员及两位匿名审稿人的宝贵意见。

（References）

Applequist S, Gahrs G E, Pfeffer R L, et al.2002.Comparison of methodologies for probabilistic quantitative precipitation forecasting [J].Wea.Forecasting, 17 (4): 783–799.

Barnston A G, Mason S J, Goddard L, et al.2003.Multimodel ensembling in seasonal climate forecasting at IRI [J].Bull.Amer.Meteor.Soc., 84 (12):1783–1796.

Bermowitz R J.1975.An application of model output statistics to forecasting quantitative precipitation [J].Mon.Wea.Rev., 103 (2): 149–153.

陈静, 陈德辉, 颜宏.2002.集合数值预报发展与研究进展 [J].应用气象学报, 13 (4): 497–507. Chen Jing, Chen Dehui, Yan Hong.2002.A brief review on the development of ensemble prediction system [J].Journal of Applied Meteorological Science (in Chinese), 13 (4): 497–507.

杜钧, 陈静.2010.单一值预报向概率预报转变的基础: 谈谈集合预报及其带来的变革 [J].气象, 36 (11): 1–11. Du Jun, Chen Jing.2010.The corner stone in facilitating the transition from deterministic to probabilistic forecast-ensemble forecasting and its impact on numerical weather prediction [J].Meteorological Monthly (in Chinese), 36 (11):1–11.

Duan Q, Ajami N K, Gao X, et al.2007.Multi-model ensemble hydrologic prediction using Bayesian model averaging [J].Advances in Water Resources, 30 (5): 1371–1386.

Fraley C, Raftery A E, Gneiting T.2010.Calibrating multimodel forecast ensembles with exchangeable and missing members using Bayesian model averaging [J].Mon.Wea.Rev., 138 (1): 190–202.

Glahn H R, Lowry D A.1972.The use of model output statistics (MOS) in objective weather forecasting [J].J.Appl.Meteor., 11 (8): 1203–1211.

Gneiting T, Raftery A E.2005.Weather forecasting with ensemble methods[J].Science, 310 (5746): 248–249.

Gneiting T, Raftery A E.2007.Strictly proper scoring rules prediction and estimation [J].J.Amer.Stat.Assoc., 102 (477): 359–378.

Grimitt E P, Mass C F.2002.Initial results of a mesoscale short-range ensemble forecasting system over the Pacific Northwest [J].Wea.Forecasting, 17 (2): 192–205.

Hamill T M, Whiltaker J S, Wei X.2004.Ensemble re-forecasting:Improving medium-range forecast skill using retrospective forecasting [J].Mon.Wea.Rev., 132: 1434–1447.

Krzysztofowicz R, Maranzano C J.2006.Bayesian processor of output for probabilistic quantitative precipitation forecasts [D].Ph.D.dissertation,Department of System Engineering and Department of Statistics,University of Virginia.

Li Z, Yan Z W.2009.Homogenized daily mean/maximum/minimum temperature series for China from 1960–2008 [J].Atmospheric Oceanic Science Letters, 2 (4): 237−243.

赵琳娜，吴昊，田付友，等.2010.基于TIGGE资料的流域概率性降水预报评估 [J].气象, 36 (7): 133–142. Zhao Linna, Wu Hao, Tian Fuyou, et al.2010.Assessment of probabilistic precipitation forecasts for the Huaihe basin using TIGGE data [J].Meteorological Monthly (in Chinese), 36 (7): 133–142.

Molteni F, Buizza R, Palmer T N, et al.1996.The ECWMF ensemble prediction system: Methodology and validation [J].Quart.J.Roy.Meteor.Soc., 122 (529): 73–119.

Palmer T N, Alessandri A, Andersen U, et al.2004.Development of a European multimodel ensemble system for seasonal-to-interannual prediction (DEMETER) [J].Bull.Amer.Meteor.Soc., 85 (6): 853–872.

Raftery A E, Gneiting T, Balabdaoui F, et al.2005.Using Bayesian model averaging to calibrate forecast ensembles [J].Mon.Wea.Rev., 133 (5):1155–1174.

Schmeits M J, Kok K J.2010.A comparison between raw ensemble output,(modified) Bayesian model averaging and extended logistic regression using ECMWF ensemble prediction reforecasts [J].Mon.Wea.Rev., 138(11): 4199–4211.

Smith R L, Tebaldi C, Nychka D, et al.2009.Bayesian modeling of uncertainty in ensembles of climate models [J].Journal of the American Statistical Association, 104 (485): 97–11.

Sloughter J M, Gneiting T, Raftery A E.2010.Probabilistic wind speed forecasting using ensembles and Bayesian model averaging [J].Journal of the American Statistical Association, 105 (489): 25–35.

Sloughter, J M, Raftery A E, Gneiting T, et al.2007.Probabilistic quantitative precipitation forecasting using Bayesian model averaging [J].Mon.Wea.Rev., 135 (9): 3209–3220.

田向军, 谢正辉, 王爱慧, 等.2011.一种求解贝叶斯模型平均的新方法[J].中国科学 (地球科学), 41 (11): 1679–1687. Tian Xiangjun, Xie Zhenghui, Wang Aihui, et al.2011.A new approach for Bayesian model averaging [J].Science China (Earth Science) (in Chinese), 41 (11): 1679–1687.

Vrugt J A, Diks C G H, Clark M P.2008.Ensemble Bayesian model averaging using Markov chain Monte Carlo sampling [J].Environmental Fluid Mechanics, 8 (5): 579–595.

Wilson L J, Beauregard S, Raftery A E, et al.2007.Calibrated surface temperature forecasts from the Canadian ensemble prediction system using Bayesian model averaging [J].Mon.Wea.Rev., 135: 1364–1385.

杨赤, 严中伟, 邵月红.2009.基于TIGGE集合预报的概率定量降水预报 [C]// 变化环境下的水资源响应与可持续利用——中国水利学会水资源专业委员会2009学术年会论文集.大连, 117.Yang Chi, Yan Zhongwei, Shao Yuehong.2009.Probabilistic quantitative precipitation forecasts for TIGGE ensemble forecasts [C]// Water Resources Response and Sustainable Utilization under Changing Environment—Documents of 2009 Annual Conference of the Water Resources Professional Committee of Chinese Irrigation Works Society (in Chinese).Dalian, 117.