长江下游地区不同边界层参数化方案的试验研究

徐慧燕 朱业 刘瑞 沈杭锋 王东海 翟国庆

1 浙江大学地球科学系，杭州 310027

2 中国气象科学研究院灾害天气国家重点实验室，北京 100081

3 浙江省海洋监测预报中心，杭州 310007

4 浙江省杭州市气象局，杭州 310007

1 引言

WRF (Weather Research and Forecasting) 模式是新一代中尺度数值模式，自它 2000年诞生以来的短短十年多时间，该模式在科研与业务上得到了广泛的应用，并不断更新发展。模式更新过程中主要的改进内容之一是：考虑了更加细致和更为复杂的物理过程，其中包括行星边界层的物理过程。行星边界层是直接受下垫面影响，主要响应地表的摩擦阻力、蒸发、蒸腾、热量输送、污染物排放以及影响气流变化的地形等作用（Stull, 1991）。它对于地气间动量、热量和水汽的交换有十分重要的作用，而这种作用主要是通过边界层湍流运动得以实现。尽管计算机技术突飞猛进，但当前模式仍然难以分辨次网格尺度的湍流运动，需要通过边界层参数化方法加以描述。

边界层参数化方案在数值模拟中有着重要的作用。Zhang and Zhang（2004）利用MM5进行边界层参数化方案的敏感性试验，指出不同参数化方案对地表风场、温度场的模拟存在较大的差异，其原因主要是：不同边界层参数化方案对物理过程（如垂直湍流交换）的参数处理是不同的。陈炯和王建捷（2006b）利用WRF模式中不同边界层参数化方案模拟江淮暴雨，表明降水对行星边界层物理过程非常敏感。对于不同地区边界层参数化方案敏感程度有所区别。Hu et al.（2010）通过对美国夏季东南部地区三个月的模拟对比了 WRF模式中的MYJ、YSU与ACM2边界层参数化方案，发现局地闭合的MYJ方案模拟的温度与湿度偏差最大。王颖等（2010）对兰州冬季地面温度与风速进行模拟，结果表明对兰州冬季温度日变化的模拟，MYJ方案优于YSU与ACM2方案。对于中国西北地区，MYJ方案可能有相对优势。慕建利（2009）运用WRF模式中的MYJ方案成功模拟了2007年8月8～9日发生在陕西中西部的中尺度对流系统引发的强暴雨。陈炯和王建捷（2006a）通过对北京大气边界层结构的模拟对比试验指出 MYJ方案模拟结果优于 YSU方案。王寅钧（2011）通过对青藏高原东南部模拟表明，冬季稳定边界层的条件下，MYJ方案模拟效果优于YSU方案。

虽然边界层参数化方案的试验已有不少，但对最近WRF模式的边界层参数的试验还有待深入，由于长江下游地区是我国经济较发达和人口较稠密地区，试验比较模式中的边界层参数优劣仍然十分重要。

目前数值模式中的边界层参数化处理方法通常有以下几种：一种是总体参数化方案；另一种是适用于边界层中无分层模式的地转输送定律（陈炯和王建捷，2006b）；另外还有以下几种处理方法，K闭合模式：K闭合模式运用了 K理论将湍流通量表示为涡动粘滞系数与垂直梯度的乘积（Stull，1991），WRF2.0的边界层参数化 MRF（Medium Range Forecast）参数化方案（Hong and Pan，1996）与WRF3.1.1中YSU（Yonsei University）边界层参数化方案（Hong and Pan, 1996; Hong et al., 2006）采用的都是K闭合方案（Wang et al., 2010）。湍流动能理论：湍流动能闭合方案源于 Kolmogorov湍流理论，认为湍流动量交换系数与湍流动能平方根成正比（赵鸣，2006），据此得到的关系式与运动方程及湍流动能方程构成闭合方程，方程中所含二阶矩项仍然采用K理论进行参数化处理。WRFV3.1.1中的 MYJ(Mellor-Yamada-Janjic) 边界层参数化方案 (Janjić, 2002)、MYNN2.5 (Mellor-Yamada Nakanishi and Niino Level 2.5) 边界层参数化方案 (Pagowski, 2008)、MYNN3 (Mellor-Yamada Nakanishi and Niino Level 3) 边界层参数化方案 (Mellor and Yamada，1982)、Bougeault-Lacarrere (Boulac) 边界层参数化方案 (Bougeault and Lacarrere, 1989) 采用的都是湍流动能闭合方案 (Wang et al.，2010)。Quasi-Normal Scale Elimination 边界层参数化方案在不稳定层结情况下也采用湍流动能闭合方案(Sukoriansky et al., 2005; Sukoriansky, 2008)。过渡湍流理论：按照物理空间透视法处理对象 (Stull,1991)。原始非对称对流模式 (Pleim and Chang，1992) 就是一个采用过渡湍流理论的简单过渡模式(Pleim,2006)。谱扩散理论：假定扩散系数 K随湍涡大小改变(Berkowicz and Prahm,1979; Berkowicz, 1984)。QNSE边界层参数化方案在稳定层结下采用湍流谱闭合模式发展而来的ε-K模式。ε-K模式主要是对MY方案 (Mellor and Yamada, 1982) 的动量以及热量扩散系数表达式进行了改进，其优点是保留了更多的物理过程，比如显式地区分了由于层结引起的质量水平与垂直输送的差别，考虑了湍流与波的共同作用。此外，ε-K模式描述了稳定层结下气流的一些重要特性。例如，Prandtl数对 Froude数与Richardson数的依赖，气流的各向异性及垂直扩散率的衰变等等。ε-K模式基本原理是：假设在原始方程中，所有尺度是可分辨的，假设模式由一个基准态，则可以得到小尺度的扰动解，通过集合平均，将原始方程中的一小段尺度进行消除，这样能对粘性率与热量扩散率有个校正，然后对下一尺度重复此过程（Sukoriansky and Galperin, 2008）。在不稳定层结下，仍然采用MYJ方案的计算方法。可见，QNSE边界层方案考虑了更为复杂、细致的物理过程。

2 模拟试验设置以及数据来源

本次模拟采用 NCEP1°×1°再分析资料作为初始场，每6小时更换一次边界条件，同时模拟采用双向三重嵌套，试验中心位于（30°N, 110°E），水平格距分别为：45 km, 15 km, 5 km。其中5 km的区域包含了长江下游大部分地区，模拟区域具体设置如图1所示。分析时采用第二重的模拟结果。模式所有区域垂直层共 28个σ层，模式所有区域的物理参数化方案包括：Dudhia短波辐射方案，RRTM长波辐射方案，WRF WSM5云微物理参数化方案，热量扩散（Thermal diffusion scheme）陆面过程，GS积云对流参数化方案。本文分别采用MYJ、QNSE、YSU、ACM2、MYNN2.5、MYNN3、Boulac共7个边界层参数化方案对长江下游地区的三次典型暴雨过程进行模拟，三个个例分别从初始时刻2009年7月23日08:00（北京时间，下同）、2011年6月3日08:00、2011年6月13日20:00，模拟连续积分36小时，积分时间步长为120 s，每一个积分时间步长均调用边界层方案，模拟方案具体设计如表1所示。

3 边界层参数化模拟试验

3.1 降水模拟结果分析

3.1.1 降水模拟对比试验

图2为2009年7月23日20:00～24日20:00的24小时累计降水量的实况与7种不同边界层参数化方案的第二重模拟结果。实况 24小时雨量呈东西带状分布在长江下游流域（图 2a），自西向东在安徽黄山与湖北通山一带分别存在160 mm、100 mm以上的2个强降水中心，分别称为A、B中心。从大尺度形势场上来看，7种不同边界层参数化方案对海平面气压、850 hPa高度场、流场，500 hPa温度场与高度场的模拟大致相当，都能较好地反映主要的天气形势。从24小时降水的模拟结果来看，湍流动能类方案 [MYJ（图 2c）、MYNN2.5（图 2f）、MYNN3（图 2g）、QNSE（图 2b）、Boulac（图 2h）]较好地反映出了降水区的南北宽度与东西走向，其中QNSE（图2b）方案与实况更接近；YSU（图2d）方案大致反映了降水区的东西走向，但没能反映出雨区的南北宽度；ACM2（图2e）方案模拟的降水集中，没能反映出降水区的带状分布特征。与实况24 h累计降水量的A、B暴雨中心对比发现，不同边界层参数化方案试验还存在较大的差异。对实况A中心，只有MYJ（图 2c）与QNSE（图2b）方案较好地模拟了中心的位置，但 MYJ（图 2c）模拟的强度偏强，QNSE（图2b）比MYJ（图2c）减少了20.2 mm，更接近实况，这可能得益于QNSE方案显式地区分了由层结引起的质量水平与垂直输送的差别。对实况B中心，QNSE（图2b）方案模拟的强度与位置相对比较接近实况。

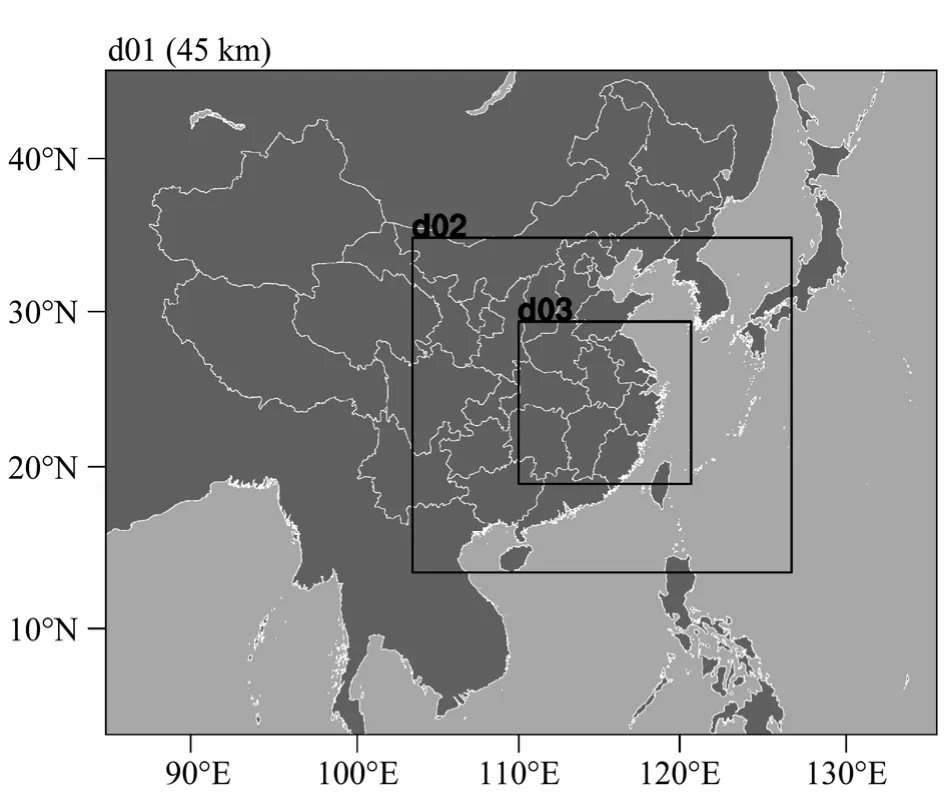
图1 模拟区域设置Fig.1 Map of model domains

表1 模拟试验方案设计Table 1 A summary of different numerical experiments

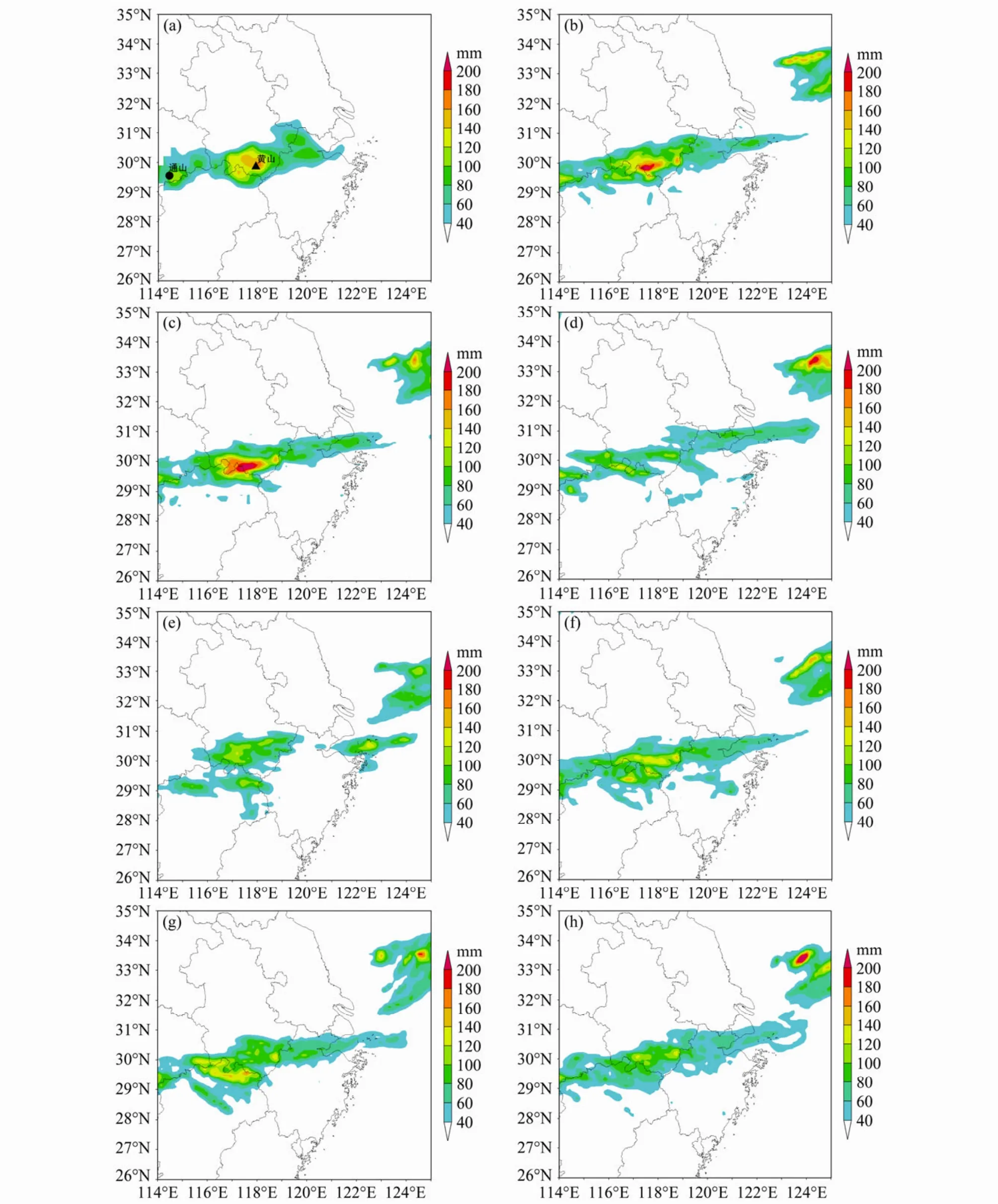
图2 2009年7月23日20:00～24日20:00不同边界层参数化方案的24 h降水模拟结果与实况 (单位：mm)：(a) 实况降水； (b) QNSE；(c) MYJ；(d) YSU；(e) ACM2；(f) MYNN2.5；(g) MYNN3；(h) Boulac。●：湖北咸宁市通山县；▲：安徽黄山市黟县Fig.2 24-hour accumulated precipitation with different planetary boundary layer schemes during 2000 LST 23 Jul-2000 LST 24 Jul, 2009: (a) Observed precipitation；(b) QNSE；(c) MYJ；(d) YSU；(e) ACM2；(f) MYNN2.5；(g) MYNN3；(h) Boulac.●: Tongshan county of Xianning in Hubei Province; ▲:Yi county of Huangshan in Anhui Province

总体而言，就以上7种边界层方案，QNSE方案相对是较优的。以相同的方法分别对 2011年 6月3日20:00～4日20:00、2011年6月14日08:00～15日08:00的24小时累计降水量的实况与7种不同边界层参数化方案的第二重模拟结果进行分析（图略），也得到了类似的结论。

通过以上不同边界层参数化方案的三次长江下游地区暴雨过程的试验比较，得到了定性较优边界层参数化方案，为了得到不同边界层参数化方案降水分布定量上的差异，还有必要进行降水模拟检验。

3.1.2 降水模拟检验

为了定量分析7种不同边界层参数化方案降水模拟结果的差异，将实况降水与模拟后插值到测站的预报值作统计检验。图3为3个个例降水检验的站点分布情况，样本站点分别涵盖了受3次降水影响的绝大多数地区，共计站点分别为3342、5933、5742个。本次统计检验采用Ts评分进行评定，将降水等级划分为三个等级：有降水发生但在暴雨量级以下(≥0.1 mm 且＜50 mm)、暴雨 (≥50 mm且＜100 mm)、大暴雨 (≥100 mm且＜200 mm)，为简便起见，将这三个降水等级分别记为：[0.1,0)、[50, 100)、[100, 200)。

Ts (threat score) 评分公式为：

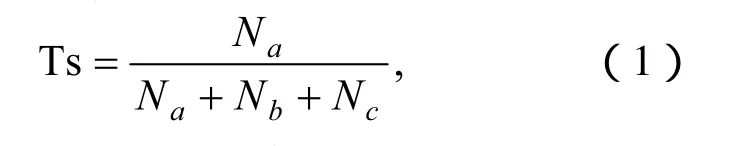
其中aN、bN、cN、dN的定义如表2，例如aN表示在降水检验区内，实况与模拟都出现在某一降水等级内的站点数。

Ts评分值表示模拟出现在某一降水等级内的准确率。表3为3例暴雨不同边界层参数化方案对于不同等级降水的评分结果，粗体字表示7个边界层参数化方案中的较优者。由表3可见，对于暴雨以下量级的降水[0.1, 50），QNSE与MYJ方案优于其他边界层参数化方案，其中 QNSE方案又优于MYJ方案；对于暴雨量级的降水，QNSE方案与MYJ方案的优势更加明显，其中QNSE方案又优于MYJ方案。同样对于2009年7月23日与2011年6月14日的大暴雨量级降水，QNSE方案的评分结果相对是最优的。以上评分结果与对降水的定性分析结果基本一致。

表2 降水检验分类表Table 2 The frequency of "yes" and "no" forecasts and occurrences

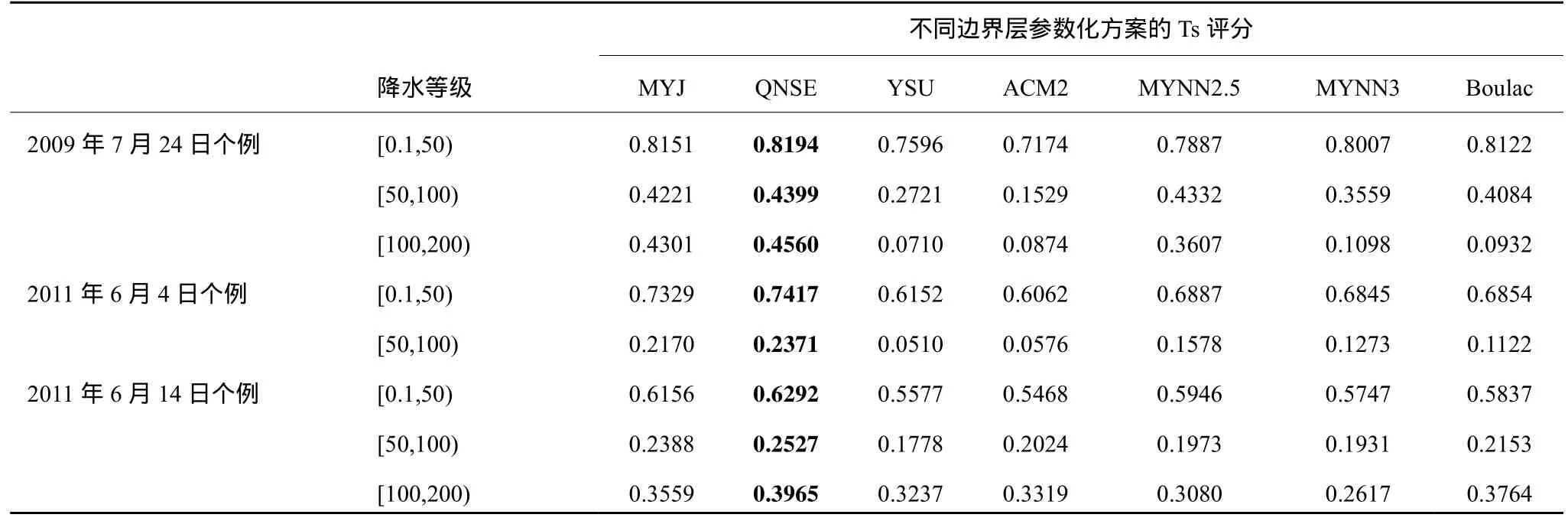
表3 不同边界层参数化方案对于不同等级降水的评分结果Table 3 Verification results of different precipitation intensities for different PBL schemes

3.2 基本要素的模拟检验

3.2.1 地面风场与温度的误差检验

为了进一步比较不同边界层参数化方案的差异，定量地验证QNSE边界层参数化方案的相对优越性，下面分别给出3例暴雨主要降水时段的降水区域内所有站点的地面风场与温度的平均绝对误差。实况风场资料分别是 2009年 7月 24日03:00～24日14:00的12个时次、2011年6月3日21:00～4日20:00、2011年6月14日09:00～15日08:00的24个时次的地面站资料。表4与表5分别为不同边界层参数化方案的地表风速与温度的误差检验结果。由表4可见，不同边界层参数化方案模拟的风速与实况风速的平均绝对误差不超过 3 m s–1，其中2011年6月4日与2011年6月14日这两例暴雨的QNSE方案模拟的风速与实况风速的平均绝对误差分别为 1.3 m s–1、1.5 m s–1，相对优于其他边界层参数化方案，从三例暴雨的平均值来看，QNSE相对是最优的。由表5可见，不同边界层参数化方案模拟的温度与实况温度的平均误差约在2℃左右，其中2009年7月23日过程与2011年6月4日过程的QNSE方案模拟的温度相对实测温度的平均绝对误差最小，相对优于其他方案，从三例暴雨的平均值来看，QNSE相对是最优的。从以上的地面降水、风速和地面温度检验结果来看，QNSE方案模拟效果最优。这可能与QNSE方案考虑了湍流与波的共同作用、气流各向异性、垂直扩散率的衰变等更为细致的物理过程有关。

3.3 边界层结构分析

为了对比不同边界层参数化方案对边界层热量、水汽输送的模拟情况，下面分别选择三例暴雨使用不同边界层参数化方案模拟存在较大差异的强降水区域，并分析所选强降水区附近的位温廓线与水汽混合比廓线（所选垂直廓线区域位置参见图7）。图4给出了2009年7月24日20:00时黄山东至附近（29.5°N～30°N, 117°E～117.5°E）强降水区与湖北通山附近（29.6°N～29.8°N, 114.6°E～114.8°E）强降水区的位温（图4a、4c）和水汽混合比廓线（图4b、4d）。图中黑色粗线为实况（源于 NCEP再分析资料）。

由湖北通山附近强降水区的位温廓线（图4a）可知，位温随高度递增，500 m以下递增率略大于500 m以上递增率，QNSE方案模拟的位温较好地反映了这一情况。从实况水汽混合比廓线（图4b）看，水汽混合比随高度递减，500 m以下递减率略大于500 m以上递减率，从地面到500 m有稳定边界层存在，500 m到800 m由原来的对流层演化为夜间的夹卷层，800 m到1000 m为对流层，QNSE方案模拟的水汽混合比廓线反映了高达500 m的稳定边界层，500 m到1000 m为对流层，相对接近实况的边界层结构特征。

表4 不同边界层参数化方案的地表风速的误差检验结果Table 4 Error test results of surface speed for different planetary boundary layer schemes

表5 不同边界层参数化方案的近地面温度的误差检验结果Table 5 Error test results of surface temperature for different planetary boundary layer schemes, the bold one denotes the best of all the PBL parameterizations

图3 降水评分的站点分布与24小时实况降水：(a) 2009年7月23日20:00～24日20:00；(b) 2011年6月3日20:00～4日20:00；(c)2011年6月14日08:00～15日08:00。黑点：站点所在位置Fig.3 Locations of observation sites (black dots) for spatial verification：(a) Rainfall from 2000 LST 23 Jul to 2000 LST 24 Jul, 2009; (b) rainfall from 2000 LST 3 Jun to 2000 LST 4 Jun, 2011; (c) rainfall from 0800 LST 14 Jun to 0800 LST 15 Jun, 2011

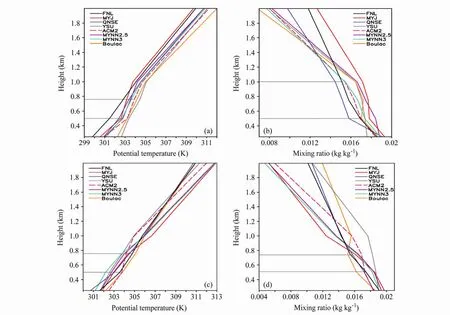
图4 2009年7月24日20:00不同边界层参数化方案下的区域平均位温（a、c）与水汽混合比（b、d）廓线：(a、b) 黄山东至附近；(c、d) 湖北通山附近Fig.4 Mean profiles of (a, c) potential temperature and (b, d) water vapor mixing ratio at 2000 LST 24 Jul 2009 simulated with different PBL schemes in the WRF model：(a, b) Dongzhi county of Huangshan city; (c, d) Tongshan city of Hubei Province

由东至附近的实况位温廓线（图4c）可知，地面至500 m为稳定边界层，500 m到740 m为夜间残留层，QNSE方案的位温廓线较好地反映了边界层的这一结构特征，另外QNSE方案模拟的位温递增率与实况相对最接近，且QNSE方案模拟的位温廓线在880 m以上与实况几乎重合。从水汽混合比廓线（图4d）可见，水汽混合比随高度递减，740 m以下的递减率小于740 m以上的递减率，QNSE方案的模拟结果较好地反映了水汽混合比的这一变化情况，且递减率与实况相对最接近，相对优于其他边界层参数化方案。

图5给出了池州以东的强降水区（29.8°N～30.2°N, 116.5°E～117.5°E）与池州以西的强降水区（29.8°N～30.2°N, 117.5°E～118.5°E）的位温与水汽混合比廓线。其中黑色线条为实况，源于NCEP再分析资料。由池州以西强降水区的位温廓线（图5a）可知，位温随高度递增，而且530 m以下的递增率大于530 m以上的递增率，除了ACM2边界层参数化以外的各个参数化方案都模拟出了位温随高度的递增情况，但是QNSE与MYJ方案与实况最为接近。池州以西的强降水区的水汽混合比廓线（图5b）比较典型，近地层存在厚度高达530 m的超绝热层。QNSE方案较好地模拟了边界层的这一结构特征，这可能与QNSE方案通过尺度消去算法考虑了稳定层结下气流的一些重要特性有关。从图（图5b）上看，从地面至530 m为逆温层，水汽混合比随高度递增，530 m以上随高度递减，QNSE方案与 MYJ方案的模拟结果都较好地反映了这一情况，而且在530 m以下，QNSE方案的递增率几乎与实况相同。由池州以东强降水区的位温廓线（图5c）可知，7种不同边界层参数化方案都模拟出了位温随高度递增的实况，但是QNSE方案相对其他方案更接近实况。从水汽混合比廓线（图5d）来看，从500 m至1 km为水汽混合比随高度变化很小的对流层， QNSE方案较好地模拟了边界层的这一结构特征。因此，总体而言，QNSE边界层参数化方案对池州附近强降水区的边界层结构的模拟相对较优。

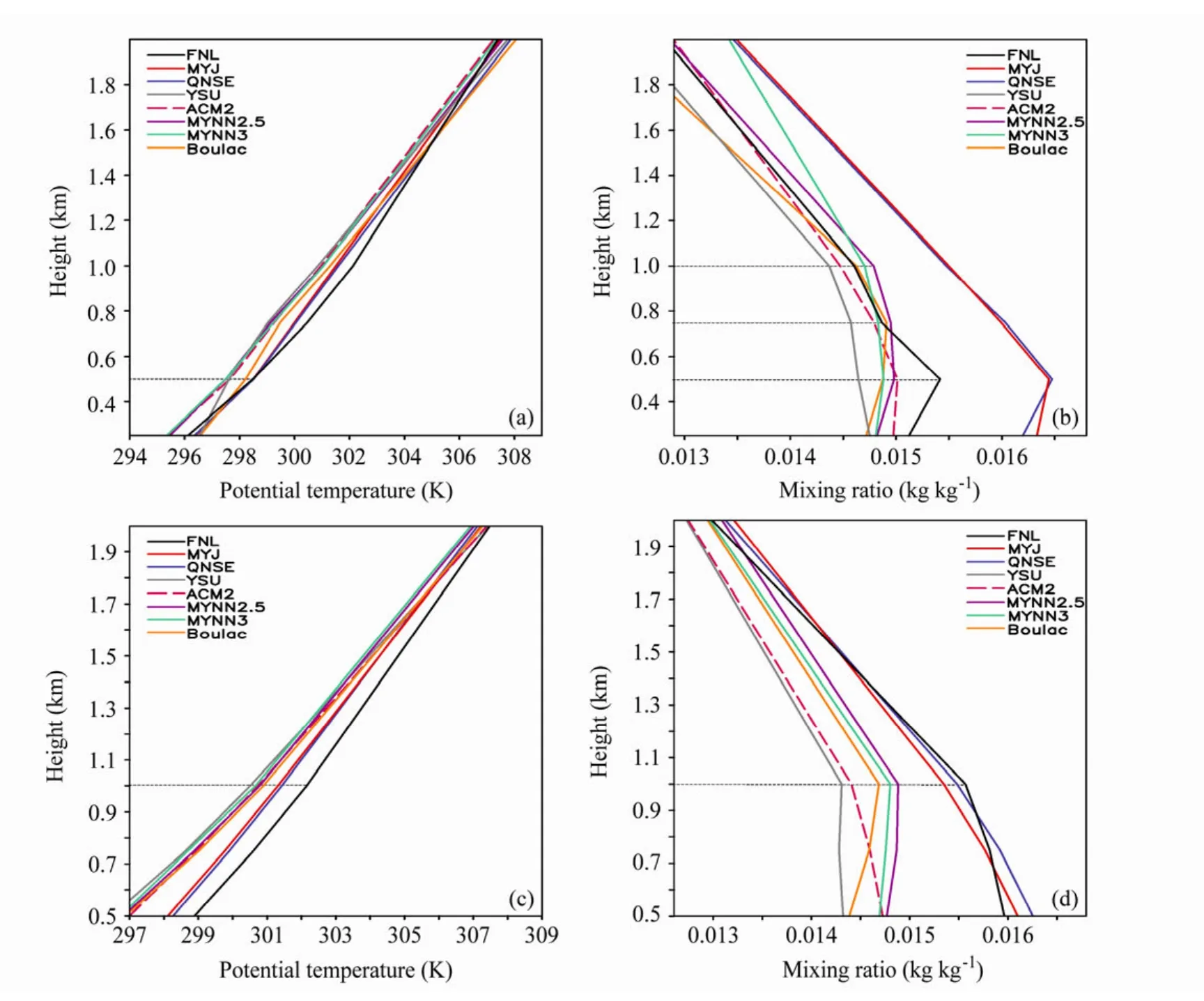
图5 2011年6月4日20:00不同边界层参数化方案下的区域平均位温（a、c）和水汽混合比（b、d）廓线：(a、b) 池州以西；(c、d) 池州以东Fig.5 Mean profiles of (a, c) potential temperature and (b, d) water vapor mixing ratio at 2000 LST 4 Jun 2011 simulated with different PBL schemes in the WRF model: (a, b) West of Chizhou city of Anhui Province; (c, d) east of Chizhou city of Anhui Province

图6给出了2011年6月15日08:00时湖北大冶附近（29.7°N～30°N, 114.5°E～115.5°E）强降水中心的位温廓线与水汽混合比廓线。其中黑色线条为实况，源于NCEP再分析资料。由位温廓线图（图6a）可知，从地面至500 m，位温随高度递增，之后以相对较大的递增率递增到 760 m，再以更大的递增率增加到1000 m，1000 m以上递增率减小，QNSE相对较好地反映了位温随高度的这一递增情况。从水汽混合比廓线图（图6b）上可以清晰地看到边界层的结构特征。从地面至500 m是水汽混合比随高度递减的稳定边界层，且500 m至760 m为夜间残留层，760 m至1000 m出现水汽混合比随高度变化很小的对流层，QNSE方案模拟的水汽混合比廓线与实况比较接近，较好地反映了边界层的这一结构特征。总体而言，QNSE方案对湖北大冶附近强降水区的边界层结构的模拟相对接近实况，这一结论与对不同边界层参数化降水模拟的分析结果一致（图略）。

5 结论与讨论

利用WRF模式最新版本中的7种边界层参数化方案，逐一试验对长江下游降水的模拟影响，来比较模式中边界层参数化的效果。通过 2009年、2011年的三次典型暴雨过程模拟试验及对降水、基本要素场的统计检验和边界层结构的廓线分析，得到了以下结论：

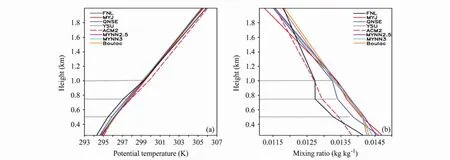
图6 2011年6月 14日08:00时，不同边界层参数化方案下的湖北大冶区域平均位温（a）和水汽混合比廓线（b）Fig.6 Mean profiles of (a) potential temperature and (b) water vapor mixing ratio over Daye city of Hubei Province at 0800 LST 14 Jun 2011, simulated with different PBL schemes in the WRF model

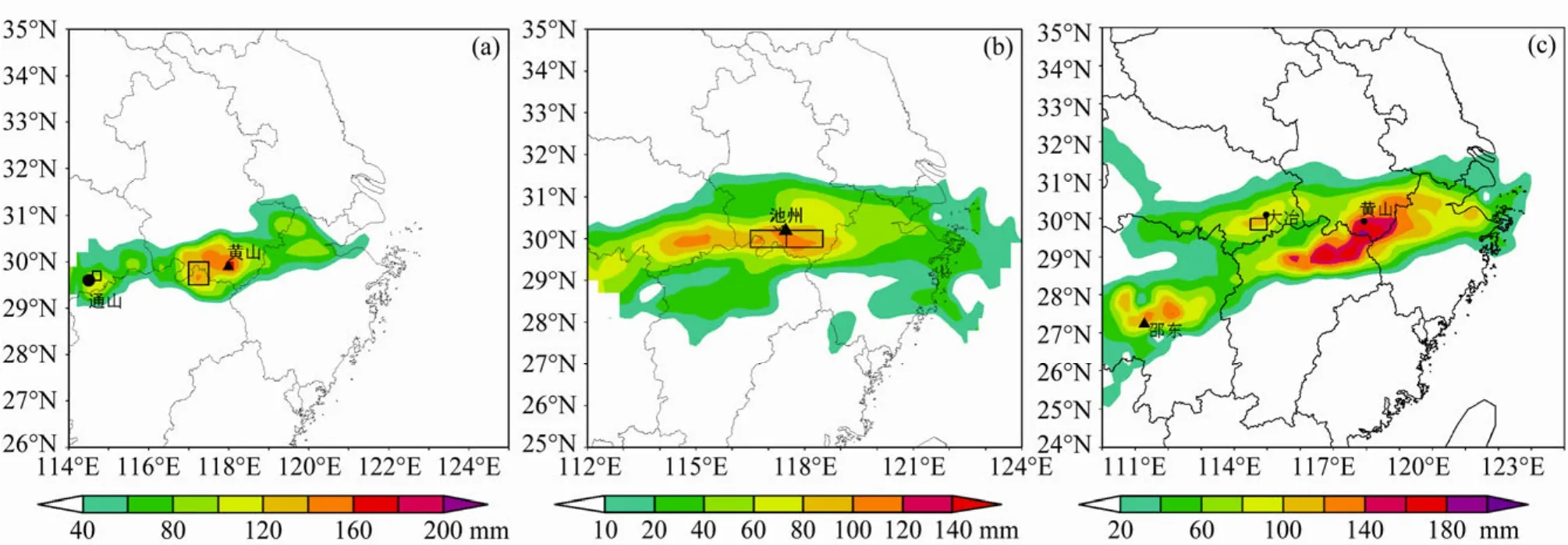
图7 长江下游三次暴雨过程实况24小时累计降水：（a）2009年7月23日20:00～24日20:00，方框分别表示湖北通山附近 (29.6°N～29.8°N, 114.6°E～114.8°E) 降水区和黄山东至县附近 (29.5°N～30°N, 117°E～117.5°E) 强降水区；(b) 2011年6月3日20:00～4日20:00，方框分别表示池州以西的强降水区 (29.8°N～30.2°N, 117.5°E～118.5°E) 和池州以东的强降水区 (29.8°N～30.2°N, 116.5°E～117.5°E)；（c）2011 年 6 月 14 日 08:00～15 日 08:00,方框表示湖北大冶附近 (29.7°N～30°N, 114.5°E～115°E) 强降水区Fig.7 24-hour accumulated precipitation in three rainstorm cases in the lower reaches of the Yangtze River: (a) Rainfall from 2000 LST 23 Jul to 2000 LST 24 Jul, 2009, rectangles represent rainstorm area of Tongshan city (29.6°N–29.8°N, 114.6°E–114.8°E) and rainstorm area of Huangshan city (29.5°N–30°N,117°E–117.5°E); (b) rainfall from 2000 LST 3 Jun to 2000 LST 4 Jun, 2011, rectangles represent rainstorm areas west of Chizhou city (29.8°N–30.2°N,117.5°E–118.5°E) and east of Chizhou city (29.8°N–30.2°N, 116.5°E–117.5°E); (c) rainfall from 0800 LST 14 Jun to 0800 LST 15 Jun, 2011, rectangle represents rainstorm area of Daye city (29.7°N–30°N, 114.5°E–115°E)

（1）从以上个例的降水试验结果来看，QNSE方案与MYJ方案模拟的24 h雨量分布优于其他边界层参数化方案，Ts评分结果也证实了以上结论，同时表明QNSE方案相对是最优。

（2）从Ts评分、地面全风速的误差检验结果来看，相对其他边界层参数化方案，QNSE方案的平均绝对误差偏差是较小的；由三例暴雨的平均绝对误差的平均结果可以看出，QNSE方案相对较优。

（3）从位温与水汽混合比的廓线来看，QNSE方案较好地模拟了强降水区的边界层结构。在WRFV3.1.1中，采用不同边界层参数化方案对长江下游降水模拟还是有比较明显的差异。总体而言，湍流动能方案优于一阶闭合方案。此外，各个湍流动能方案之间也存在明显的差异，这可能与不同TKE方案采用不同闭合技术有关。MYNN2.5方案与MYNN3方案原理上是类似的，只是所保留的最高阶预报方程不同；MYJ与QNSE方案在不 稳定层结下采用相同的原理，在稳定层结下采用不同的技术，通过计算各向互异的湍流谱，QNSE方案得到了稳定层结下各向互异的湍流动量扩散系数与热量扩散系数，考虑了稳定层结下能量水平输送与垂直输送的差异，水平气流分量的增加往往以垂直气流分量的减小为代价。同时表明：Richardson数存在一个范围，在此范围内，涡动粘滞系数与扩散系数急剧地递减，即使Richardson数很大，湍流也并不完全消失。ACM2方案与YSU方案假定存在临界 Richardson数，当 Richardson数大于临界Richardson数时，则认为湍流消失。这可能正是QNSE方案表现相对优于其他方案，尤其优于YSU与 ACM2方案的原因之所在。Boulac方案是为预报晴空湍流的位置与强度而引进的一种TKE方案，这些方案最明显的一个差异是采用不同原理计算湍流混合长，这导致边界层的湍流混合强度不同而影响模拟结果。

由于计算条件与观测资料的限制，我们主要针对长江下游的3例暴雨进行模拟试验，今后随着条件改进，可以选择更多个例进行模拟对比，以期取得更有价值的研究结果。

References)

Berkowicz R.1984.Spectral methods for atmospheric diffusion modeling[J].Bound.-Layer Meteor., 30: 201–219.

Berkowicz R, Prahm L P.1979.Generalization of K theory for turbulent diffusion.Part 1: Spectral turbulent diffusivity concept [J].J.Appl.Meteor., 18: 266–272.

Bougeault P, Lacarrere P.1989.Parameterization of orography-induced turbulence in a mesobeta-scale model [J].Mon.Wea.Rev., 117:1872–1890.

陈炯, 王建捷.2006a.北京地区夏季边界层结构日变化的高分辨模拟对比 [J].应用气象学报, 17 (4): 406–407. Chen Jiong, Wang Jianjie.2006a.Diurnal cycles of the boundary layer structure simulated by WRF in Beijing [J].Journal of Applied Meteorological Science (in Chinese), 17(4): 406–407.

陈炯, 王建捷.2006b.边界层参数化方案对降水预报的影响 [J].应用气象学报, 17 (增刊): 11–17. Chen Jiong, Wang Jianjie.2006b.Mesoscale precipitation simulation sensitivity to PBL parameterization [J].Journal of Applied Meteorological Science (in Chinese), 17 (Suppl.): 11–17.

Hong S Y, Pan H L.1996.Nonlocal boundary layer vertical diffusion in a medium-range forecast model [J].Mon.Wea.Rev., 124: 2322–2340.

Hong S Y, Noh Y, Dudhia J.2006.A new vertical diffusion package with an explicit treatment of entrainment processes [J].Mon.Wea.Rev., 134:2318–2341.

Hu X M, Nielsen-Gammon J W, Zhang F Q.2010.Evaluation of three planetary boundary layer schemes in the WRF model [J].Journal of Applied Meteorology and Climatology, 49: 1831–1844.

Janjić Z I.2001.Nonsingular implementation of the Mellor-Yamada Level 2.5 scheme in the NCEP MESO model [R].NCEP Office Note No.437,61pp.

Mellor G L, Yamada T.1982.Development of a turbulence closure model for geophysical fluid problems [J].Rev.Geophys.Space Phys., 20:851–875.

慕建利.2009.陕西关中强暴雨中尺度对流系统研究 [D].南京气象学院博士学位论文, 111–116. Mu Jianli.2009.Study on MCS of the heavy rainfall event in the middle part of Shaanxi [D].Ph.D.dissertation(in Chinese), Nanjing University of Information Science and Technology,111–116.

Pagowski M.2008.Nakanishi and Niino improved Mellor-Yamada 1.5 and 2-order closures (2004, 2006) implementation in WRF & 1D WRF PBL model as a tool for development and testing [R].WRF Users’ Workshop,PBL Group Meeting, Boulder, CO, USA.

Pleim J E.2006.A combined local and nonlocal closure model for the atmospheric boundary layer.Part I: Model description and testing [J].Journal of Applied Meteorology and Climatology, 46: 1383–1395.

Pleim J E, Chang J S.1992.A non-local closure model for vertical mixing in the convective boundary layer [J].Atmos.Environ., 26A: 965–981.

Stull R B.1991.边界层气象学导论 [M].杨长新译, 赵鸣, 王彦校.北京: 气象出版社, 1: 2.Stull R B.1991.An Introduction to Boundary Layer Meteorology (in Chinese) [M].Yang Changxin Translated,Zhao Ming, Wang Yan Proofread.Beijing: China Meteorological Press, 1:2.

Sukoriansky S.2008.Implementation of Quasi-Normal Scale Elimination model of stably stratified turbulence in WRF [R].Report on WRF-DTC Visit of Semion Sukoriansky-June.

Sukoriansky S, Galperin B.2008.A Quasi-Normal Scale Elimination(QNSE) theory of turbulent flows with stable stratification and its application in weather forecast systems [C]// 6th IASME/WSEAS International Conference on HEAT TRANSFER THERMAL ENGINEERING and ENVIRONMENT (THE’08).Rhodes, Greece,376–380.

Sukoriansky S, Galperin B, Perov V.2005.Application of a new spectral theory of stably stratified turbulence to the atmospheric boundary layer over sea ice [J].Bound.-Layer Meteor., 117: 231–257.

王寅钧.2011.青藏高原东南部 WRF边界层模拟与观测对比探讨研究[D].南京信息工程大学理学硕士学位论文, 31–32. Wang Yinjun,2011.Contrast the simulation observation result of WRF model to bounder layer at southeast Tibetan Plateau [D].M.S.thesis (in Chinese),Nanjing University of Information Science and Technology, 31–32.

王颖, 张镭, 胡菊, 等.2010.WRF模式对山谷城市边界层模拟能力的检验及地面气象特征分析 [J].高原气象, 29 (6): 1397–1407. Wang Ying, Zhang Lei, Hu Ju, et al.2010.Verification of WRF simulation capacity on PBL characteristic and analysis of surface meteorological characteristic over complex terrain [J].Plateau Meteorology (in Chinese),2010, 29 (6): 1397–1407.

Wang W, Bruyere C, Duda M, et al.2010.WRF-ARW V3: User’s Guide [R].Mesoscale & Microscale Meteorology Division, National Center for Atmospheric Research, 5–40.

Zhang D L, Zhang W Z.2004.Diurnal cycles of surface winds and temperatures as simulated by five boundary layer parameterizations [J].J.Appl.Meteor., 43: 157–168.

赵鸣.2006.大气边界层动力学 [M].北京: 高等教育出版社, 20–25.Zhao Ming.2006.Atmospheric Boundary Layer Dynamics (in Chinese)[M].Beijing: Higher Education Press, 20–25.