带有低通滤波的广义S变换在探地雷达层位识别中的应用

张先武，高云泽，方广有＊

1 中国科学院电子学研究所，北京 100190

2 中国科学院大学，北京 100049

1 引 言

在浅层地球物理勘探中，探地雷达以其无损、高效、高分辨率等优点正越来越受到人们的重视[1-5］.作为探地雷达的常见勘探目标，如冰川、公路路基等，通常可被视为层状介质[6-9］.准确识别这些层状介质的层位信息（深度、厚度等）对后续处理和解释探地雷达数据至关重要[10］.电磁波在这些层状介质中传播时，会产生衰减和频散现象[11-15］，造成探地雷达接收到的回波信号为时变信号.利用回波信号的时变特性可以为识别层状介质的层位信息提供帮助.

对于时变信号，人们提出了一系列信号分析和处理方法，如短时Fourier变换（STFT）[16］、小波变换（WT）[17］、S变换[18］等.同 WT、STFT 等时间-频率域信号处理方法相比，S变换具有很多独特优点，如时间-频率域的分辨率与频率相关；S变换谱与Fourier变换谱保持直接联系；S变换的基本小波不用满足容许性条件等[19-21］.

探地雷达勘探中，雷达信号穿过由层厚小于调谐厚度的薄层构成的层序列时，反射的雷达信号的频率会增高[22-24］.依据此特点，利用S变换可以对这种薄层序列进行有效识别[25］.为了获得层的厚度、深度等信息，需要S变换具有较高的时间分辨率[26-27］.而S变换的时窗函数固定，不能根据需要来调节时间分辨率.对此，本文对S变换的时窗函数加以改进，使其可调.针对变换中提高时间分辨率会降低频率分辨率的问题，本文将低通滤波函数融入到时窗函数中，来调节变换中的频率分辨率.通过算例，文中对改进后的广义S变换与S变换进行了对比分析，同时将广义S变换应用到实测探地雷达资料的层位识别中，提高了S变换的层位识别能力.

2 基本原理

2.1 S变换

Stockwell给出函数h（t）的S变换定义如下[18］：

式中，t，τ表示时间，f表示频率，均为实数.

定义S变换的时窗函数为G（t，f），

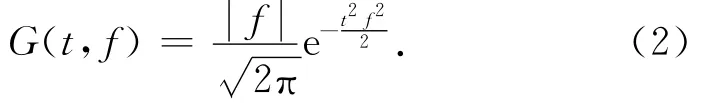
S变换的时窗函数G（t，f）要满足以下条件[28］，即

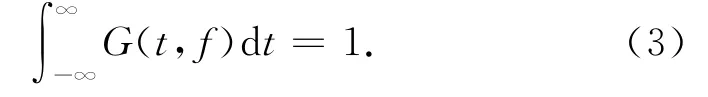
在满足（3）式的条件下，可以得到：

（4）式中，H（f）为函数h（t）的Fourier变换.由此可以得到S变换的反变换为：

为了提高计算效率，通常不是直接按照（1）式在时间域实现S变换，而是在频率域实现.频率域S正变换公式为：

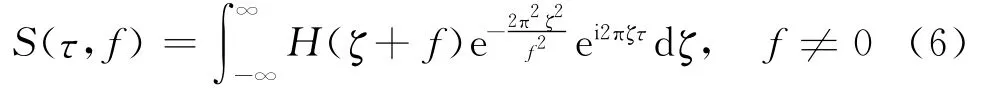
2.2 广义S变换

为了使广义S变换的时窗函数可调，将低通滤波函数融入其中，同时在时窗函数中引入调节参数.通过改变调节参数的大小来调节广义S变换的时间分辨率和频率分辨率.

定义广义S变换的时窗函数为W（t，f，λG，λL），W （t，f，λG，λL）=

式中，λG，λL表示的是不同的调节参数.λG主要用来调节时窗的宽度，λG越大，时窗越窄，广义S变换的时间分辨率越高，但是同时会降低变换的频率分辨率.此时再通过调节λL，对广义S变换的频率分辨率进行调节，λL越小，广义S变换的频率分辨率越高.

广义S变换的时窗函数 W （t ，f，λG，λL）满足S变换的时窗函数条件，即

定义广义S变换如下：

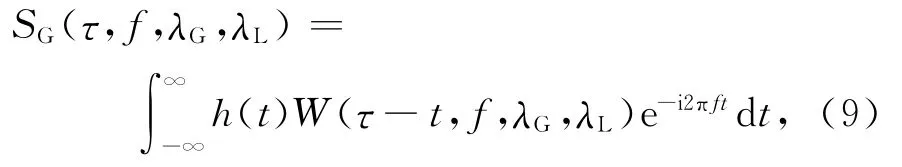
在满足（8）式的条件下，可以得到：

（10）式中，H（f）为函数h（t）的 Fourier变换.由此可以得到广义S变换的反变换为：

同S变换类似，为了提高计算效率，可以在频率域实现广义S变换.变换公式为：

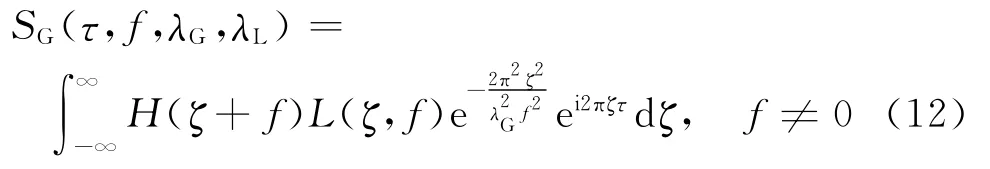
（12）式中L（ζ，f）为：为了保证广义S正、反变换完全可逆.当f=0时，广义S正变换满足：

在计算机上实现广义S变换时，采用（12）和（13）式的离散形式.

3 对比分析

为了研究广义S变换分析时变信号的特点，合成一个时变信号h（t）.h（t）的解析式为：

信号h（t）主要包含三个频率成分，分别为100Hz、200Hz、300Hz.各个频率成分起止时间对应分别为：0～449ms、274～723ms、550～999ms.计算机上处理时，需要先对上述信号h（t）进行采样，本文采用的采样时间间隔为1ms，总的采样时间为999ms.图1为信号h（t）采样后的示意图.

图1 合成时变信号采样后示意图Fig.1 Sketch of sampling results of synthetic time-varying signal

3.1 合成信号的S变换

为了对比分析广义S变换和S变换，对信号h（t）进行S变换，图2为S变换结果.图2中，信号的频率成分以及各个频率成分的起止时间能很好地与合成信号相对应.随着信号频率的增大，S变换的频率分辨率降低，时间分辨率增高，这同小波变换相似.

图2 合成时变信号S变换结果Fig.2 S transform results of synthetic time-varying signal

3.2 合成信号的广义S变换

3.2.1 调节参数λG对广义S变换的影响

为了分析调节参数λG对广义S变换的影响，先固定参数λL（文中固定λL为10），再调节λG.对不同的λG，分别对信号h（t）进行广义S变换.图3显示了λG对广义S变换的影响.从图3中可以看到，在λL不变的情况下，随着λG的增大，广义S变换的时间分辨率在增大，λG=1时，广义S变换结果与S变换结果相同，当λG＞1时，广义S变换的时间分辨率比S变换的高.但是，随着λG的增大，广义S变换的频率分辨率在减小.λG=2时，由于频率分辨率过低，在550～723ms时间段内，200Hz和300Hz频率成分相互重叠，此时，在广义S变换后的时间-频率域内已经无法将它们识别出来.

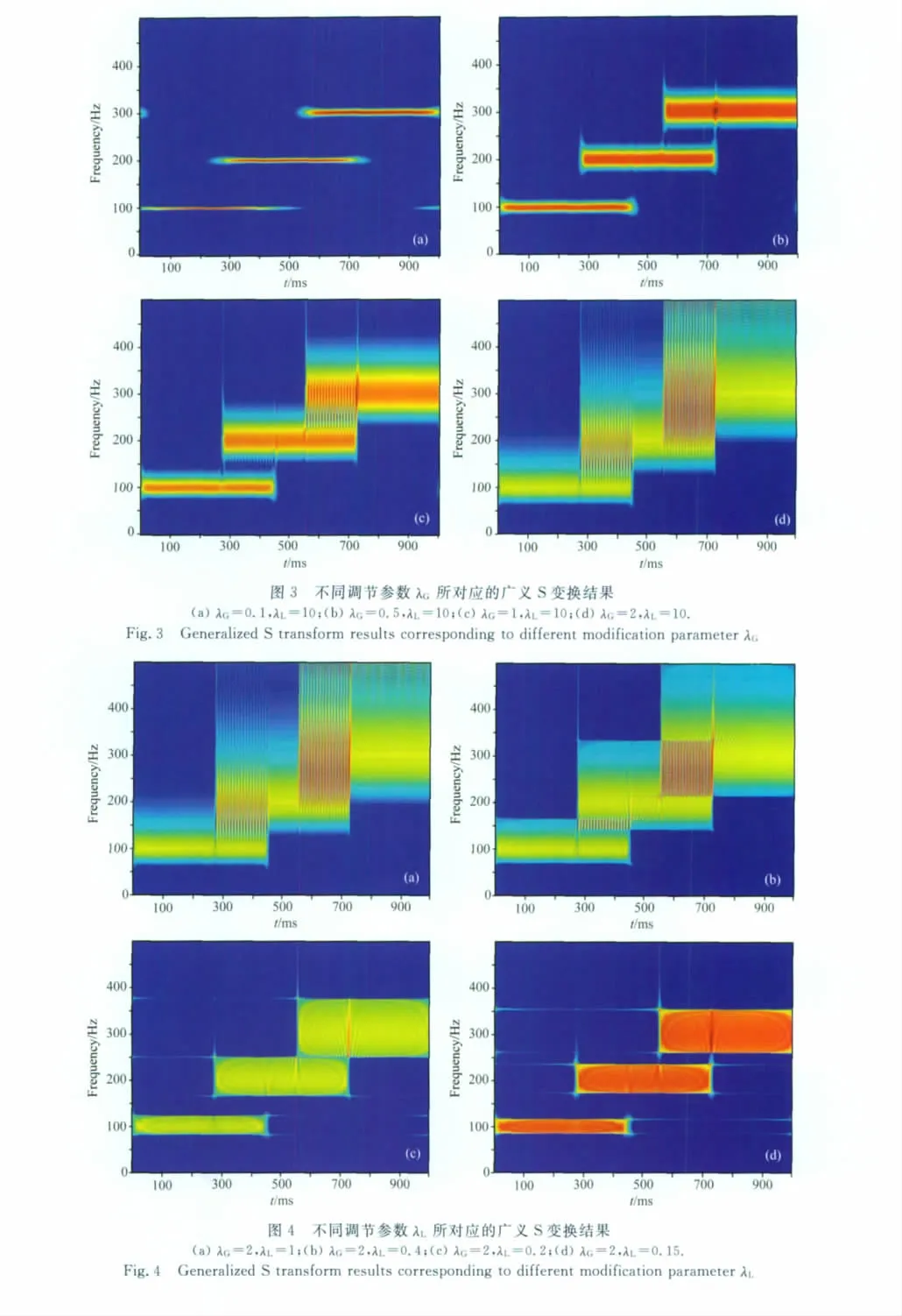
3.2.2 调节参数λL对广义S变换的影响

固定λG（文中固定λG为2），调节λL，对不同的λL，分别对信号h（t）进行广义S变换，变换结果为图4.

对比图4a和图3d，两者变换结果相同，在550～723ms时间段内，无法将200Hz和300Hz频率成分识别出来.随着λL的减小，广义S变换的频率分辨率在增大，λL≤0.2时，200Hz和300Hz频率成分逐渐分离，此时在时间-频率域内已经可以将它们识别出来.由图4a和图3d所对应的变换结果相同，表明在λG不变的情况下，λL增大到某一数值后，广义S变换结果不发生改变.当λG=1，λL=+∞时，对任何信号，广义S变换与S变换结果相同.

4 广义S变换识别实测探地雷达资料的层位

图5为某一湖区实测探地雷达资料.测量时，天线中心频率选用150MHz，采用的时间窗口为500ns，采样点数为512.总的记录道数为141道.本文对其中的第90道（图6）进行分析，分别对其进行S变换和广义S变换，图7为S变换结果.

对实测探地雷达数据进行广义S变换时，需要确定合适的调节参数λG和λL.选取λG和λL时，可以先确定λL（一般可令λL为1），再根据变换结果来调节λG，λG越大，广义S变换的时间分辨率越高.调节λG时，可先取λG为1，再逐渐增大λG，对比分析不同λG对应的广义S变换结果.当变换结果的时间分辨率随着λG的增大而变化不大时，选取此时的λG.

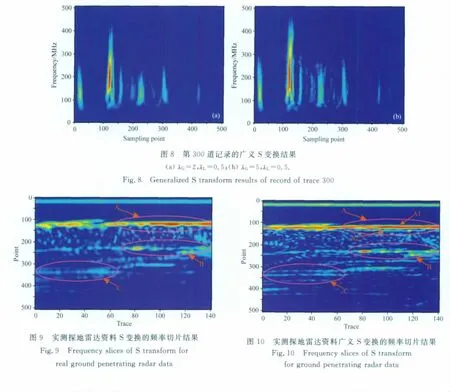
在选取λG的过程中，为了获得较高的时间分辨率，逐渐增大λG，但是同时会降低广义S变换的频率分辨率.为了对广义S变换的频率分辨率进行一定的补偿，在确定调节参数λG后，再适当减小λL，当变换结果中的不同频率成分能较好地分开时，选取此时的λL.λL不宜过小，否则会影响广义S变换的时间分辨率.图8为第90道数据的广义S变换结果，变换时选取的调节参数分别为λG=2、λL=0.5和λG=5、λL=0.5.

图5 实测探地雷达资料Fig.5 Measured ground penetrating radar data

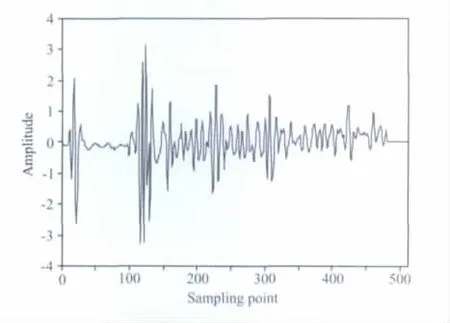
图6 实测探地雷达资料第300道记录Fig.6 Record of trace 300in ground penetrating radar data

从S变换结果（图7）中可以看到，105～135采样点间的回波信号中心频率在200MHz左右，相对于直达波的中心频率（130MHz左右）有明显提升.据此可以推断105～135采样点间的回波信号对应的为湖底淤泥沉积序列的反射回波信号，且淤泥沉积层的单层厚度小于为湖底淤泥的相对介电常数）.

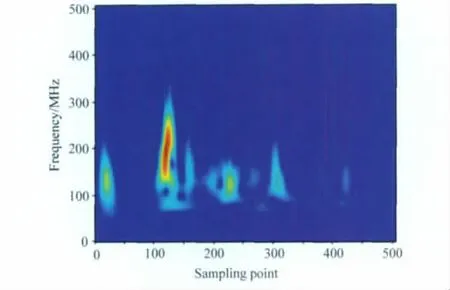
图7 第300道记录的S变换结果Fig.7 S transform result of the record of trace 300

对比分析图7、图8，105～135采样点间的回波信号在广义S变换结果（图8）中，可以被更精细地划分为两部分，前一部分信号的中心频率（相对于直达波的中心频率）有明显提升，而后一部分信号的中心频率变化不大.从而我们可以将105～135采样点间的回波信号对应的地下介质划分为两部分，前一部分对应的是湖底淤泥沉积序列，后一部分对应的是沉积序列底部的独立反射层.

为了更好地验证单道（第90道）雷达记录广义S变换分析结果，本文对实测的141道雷达数据分别进行S变换和广义S变换（变换时，取λG=5、λL=0.5）.再对变换结果进行频率切片分析（文中选用的频率为150MHz），图9和图10分别为S变换和广义S变换频率切片分析结果.从图10（A区域）中可以明显地看出，105～135采样点间地下介质可被划分为湖底淤泥沉积序列（A1）和沉积序列底部的独立反射层（A2）两部分，而在图9的相同位置，无法划分出沉积序列底部的独立反射层.频率切片分析结果也表面广义S变换提高了S变换的层位划分能力.

对比分析图7、图8，探地雷达回波信号经过广义S变换后，回波信号在时频平面内的能量分布沿时间方向上变窄，时间分辨率在增大，这一点也可以从频率切片分析结果中得到印证.对比分析图9和图10的B、C区域，图10中层位的反射回波信号清晰，能量分布沿时间方向上细窄，可以更精细地确定层位的厚度和深度信息.

5 结 论

本文在S变换的基础上，对S变换加以改进和推广，提出了一种广义S变换.通过引入调节参数，同时将低通滤波函数融入到广义S变换的时窗函数中，来调节广义S变换的时间分辨率和频率分辨率.利用广义S变换分析时变信号时，可以根据需要来选择合适的调节参数.理论信号分析和实测数据计算表面该变换具有很强的适用性.

广义S变换可以在频率域实现，有较高的计算效率.实际应用中，广义S变换的离散采样条件与S变换相同.在实测探地雷达资料的层位识别中，同S变换相比，广义S变换在确定层位深度、厚度和划分层位等方面的能力得到提高.

（References）

[1]Annan A P.Ground penetrating radar：Principles，procedures，＆applications，Sensors ＆Software Inc.Technical Paper，2003.

[2]陈义群，肖柏勋.论探地雷达现状与发展.工程地球物理学报，2005，2（2）：149-155.Chen Y Q，Xiao B X.On the status quo and development of Ground Penetrating Radar.Chinese Journal of Engineering Geophysics （in Chinese），2005，2（2）：149-155.

[3]李嘉，郭成超，王复明等.探地雷达应用概述.地球物理学进展，2007，22（2）：629-637.Li J，Guo C C，Wang F M，et al.The summary of the surface ground penetrating radar applied in subsurface investigation.Progress in Geophysics（in Chinese），2007，22（2）：629-637.

[4]Slob E，Sato M，Olhoeft G.Surface and borehole groundpenetrating-radar developments.Geophysics，2010，75（5）：A103-A120.

[5]李华，鲁光银，何现启等.探地雷达的发展历程及其前景探讨.地球物理学进展，2010，25（4）：1492-1502.Li H，Lu G Y，He X Q，et al.The progress of the GPR and discussion on its future development.Progress in Geophysics（in Chinese），2010，25（4）：1492-1502.

[6]武震，张世强，刘时银等.祁连山老虎沟12号冰川冰内结构特征分析.地球科学进展，2011，26（6）：631-641.Wu Z，Zhang S Q，Liu S Y，et al.Structural characteristics of the No.12Glacier in Laohugou Valley，Qilian Mountain based on the ground penetrating radar combined with FDTD simulation.Advances in Earth Science （in Chinese），2011，26（6）：631-641.

[7]杨天春，吕绍林，王齐仁.探地雷达检测道路厚度结构的应用现状及进展.物探与化探，2003，27（1）：79-82.Yang T C，LüS L，Wang Q R.The application and development of GPR in detection of pavement thickness and highway structures.Geophysical and Geochemical Exploration（in Chinese），2003，27（1）：79-82.

[8]冯德山，戴前伟.高速公路路面厚度探地雷达检测.地球物理学进展，2008，23（1）：289-294.Feng D S，Dai Q W.Application of ground penetrating radar in the survey of the pavement thickness in highway.Progress in Geophysics（in Chinese），2008，23（1）：289-294.

[9]秦瑶，陈洁，方广有等.基于探地雷达频谱反演法的薄层识别技术研究.电子与信息学报，2010，32（11）：2760-2763.Qin Y，Chen J，Fang G Y，et al.Research on thin-layer recognition technique based on the spectrum inversion method of Ground Penetrating Radar.Journal of Electronics &Information Technology （in Chinese），2010，32（11）：2760-2763.

[10]王惠濂，李大心，邓世坤等.探地雷达在建筑地基探测中的应用.地球科学 （中国地质大学学报），1993，18（3）：323-328.Wang H L，Li D X，Deng S K，et al.Application of Ground Penetrating Radar to construction foundation exploration.Earth Science（Journal of China University of Geosciences）（in Chinese），1993，18（3）：323-328.

[11]孙洪星，康永华.有耗介质探地雷达波传播衰减特性的研究.工程地质学报，1999，7（4）：344-348.Sun H X，Kang Y H.Study on GPR wave propagation attenuation behaviors in heterogeneous medium.Journal of Engineering Geology （in Chinese），1999，7（4）：344-348.

[12]底青云，许琨，王妙月.衰减雷达波有限元偏移.地球物理学报，2000，43（2）：257-262.Di Q Y，Xu K，Wang M Y.The attenuated radar wave migration with finite element method.Chinese Journal of Geophysics （in Chinese），2000，43（2）：257-262.

[13]Irving J D，Knight R J.Removal of wavelet dispersion from ground-penetrating radar data.Geophysics，2003，68（3）：960-970.

[14]刘四新，曾昭发.频散介质中地质雷达波传播的数值模拟.地球物理学报，2007，50（1）：320-326.Liu S X，Zeng Z F.Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium.Chinese Journal of Geophysics（in Chinese），2007，50（1）：320-326.

[15]John H B.Frequency-dependent attenuation analysis of ground-penetrating radar data.Geophysics，2007，72（3）：7-16.

[16]Gabor D.Theory of communication.Journal of the IEEE，1946，93：429-457.

[17]Gressman A，Morlet J.Decomposition of hardy functions into square integrable wavelets of constant shape.SIAM J.Math.Anal.，1984，15（4）：723-736.

[18]Stockwell R G，Mansinha L，Lowe R P.Localization of the complex spectrum：the S transform.IEEE Transactions on Signal Processing，1996，44（4）：998-1001.

[19]高静怀，陈文超，李幼铭等.广义S变换与薄互层地震响应分析.地球物理学报，2003，46（4）：526-532.Gao J H，Chen W C，Li Y M，et al.Generalized S transform and seismic response analysis of thin interbeds.Chinese Journal of Geophysics（in Chinese），2003，46（4）：526-532.

[20]刘喜武，年静波，刘洪.基于广义S变换的吸收衰减补偿方法.石油物探，2006，45（1）：9-14.Liu X W，Nian J B，Liu H.Generalized S-transform based compensation for stratigraphic absorption of seismic attenuation.Geophysical Prospecting for Petroleum（in Chinese），2006，45（1）：9-14.

[21]Pinnegar C R，Mansinha L.Time-local Fourier analysis with a scalable，phase-modulated analyzing function：the S-transform with a complex window.Signal Processing，2004，84（7）：1167-1176.

[22]Widess M B.How thin is a thin bed.Geophysics，1973，38（6）：1176-1180.

[23]Knapp R W.Vertical resolution of thick beds，thin beds and thin-bed cyclothems.Geophysics，1990，55（9）：1183-1190.

[24]Guha S，Kruse S E，Wright E E，et al.Spectral analysis of ground penetrating radar response to thin sedimentary layers.Geophysical Research Letters，2005，32：L23304，doi：10.1029／2005GL023933.

[25]Guha S，Kruse S，Wang P.Joint time-frequency analysis of GPR data over layered sequences.The Leading Edge，2008，27（11）：1454-1460.

[26]刘喜武，刘洪，李幼铭等.基于广义S变换研究地震地层特征.地球物理学进展，2006，21（2）：440-451.Liu X W，Liu H，Li Y M，et al.Study on characteristics of seismic stratigraphy by generalized S-transform.Progress in Geophysics（in Chinese），2006，21（2）：440-451.

[27]陈学华，贺振华，黄德济.时频域高分辨地震层序识别.吉林大学学报 （地球科学版），2008，38（1）：152-155.Chen X H，He Z H，Huang D J.Seismic sequence identifying with high resolution in time-frequency domain.Journal of Jilin University （Earth Science Edition） （in Chinese），2008，38（1）：152-155.

[28]Pinnegar C R，Mansinha L.The S-transform with windows of arbitrary and varying shape.Geophysics，2003，68（1）：381-385.