地震波干涉偏移及预条件正则化最小二乘偏移成像方法对比
王彦飞
中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室,北京 100029
1 引 言
通常的偏移手段对于垂向地震剖面(VSP)成像效果不是太好,因此人们发展了很多新的方法进行研究,比如近期发展起来的干涉偏移方法和偏移反演方法.干涉偏移(Interferometric migration),与光学中的干涉相关.干涉是光学物理的概念,通常指的是两列或两列以上的波在空间中重叠时发生叠加从而形成新波形的现象.Claerbout[1]指出对自由地表接收到的从底部来的透射地震记录进行自相关,等价于其自激自收模拟记录(包含负时间记录以及零时刻的脉冲响应).在忽略仪器响应的情况下,地震检波器记录到的地震信号等效于格林函数和地震子波的卷积.地震波干涉法的核心思想就是对记录的地震数据进行重新校准,得到以其中一个检波器为虚拟震源的新的地震记录.然后对虚拟震源求取格林函数并对新的地震记录进行偏移运算.地震波干涉偏移的目的是为了改善传统直接偏移方法的成像效果:如展宽成像区域并提高成像的分辨率.由于干涉思想的采用,该方法可以把弱信号(低信噪比、多次波)变为有用的信号,也就是所谓的被动源成像(Passive seismic imaging).该方法在最近的10年来得到了极大的发展[2-13].与之相对应,为了改善传统直接偏移方法的成像效果的另一种方法是地震波偏移及反演成像方法,即在传统直接偏移方法的基础上,通过增加反演迭代的次数来达到高分辨率成像的目的[14-18].
地震波偏移成像是基于对Born近似成像算子方程表达的深化.通常可以写成第一类算子表达的形式[19-21]:Lm=d.其中,L为正向模型算子(由核函数表征);m为地层反射模型;d为观测到的地震信号.在地震勘探领域,试图通过求mmig=L*d=L*Lm来得到对地层的偏移成像,其中L*为L的伴随算子,定义作 (Lx,y)= (x,L*y);mmig表示模糊的地层反射偏移图像;L*L表示模糊积分核算子,也称作分辨率函数或点扩展函数.该函数对于优化勘测规划,比如说选取最优偏移孔径,合适的采样以及选择偏移参数起着十分重要的作用.显然,对偏移成像作逆运算可以得到真实的反射模型m=(L*L)-1mmig=(L*L)-1L*d.但是,这样做的缺陷:(1)L*L是比L 更为不适定的算子,因而 (L*L)-1对数据误差/噪音高度敏感;(2)求逆运算的计算量巨大.对于偏移反演成像,发展起来的方法有基于PSF核函数的反演法[22],基于CG迭代的最小二乘法[15-16],非稳态的匹配滤波法[23],正则化反演成像法和非单调梯度迭代法[18,24-25].此外,更多的地球物理反演计算方法以期用到偏移反演计算上,如衰减的最小二乘法[26-27],带偏差原则的重开始共轭梯度法[28],全局收敛的信赖域算法和无记忆拟牛顿法[29-30],基于Bayes的统计推理的反演计算[31-33]以及奇异值展开法[17,19,34].这些方法有的已 经用到 地震偏移反演成像上.但这些方法对于偏移成像的反演计算可能收敛的非常慢[35-38].
本文研究干涉偏移方法和偏移反演成像方法对于地震成像效果的影响,探讨二者在提高成像分辨率上的异同.对于偏移反演,基于不适定性考虑以及最小二乘偏移反演计算的局限性,提出应用预条件正则化的偏移反演手段进行计算及数值模拟.
2 偏移成像原理
2.1 Born算子成像方程
设Green函数G(rg|rs)满足 Helmholtz方程
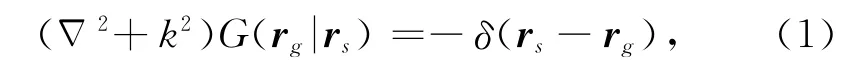
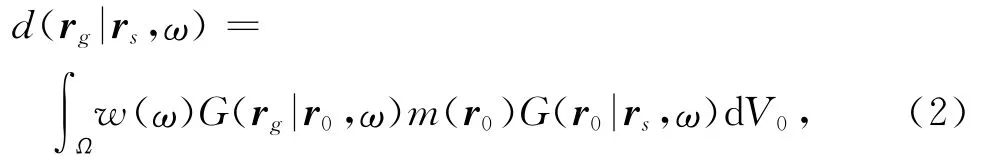
其中,d(rg|rs,ω)表示接收到的反射数据;w(ω)为频率域小波,m(r0)为地层反射函数,Ω为成像区间.定义算子L为

则得到Born算子成像方程为

由Born算子成像方程可以得到偏移公式:
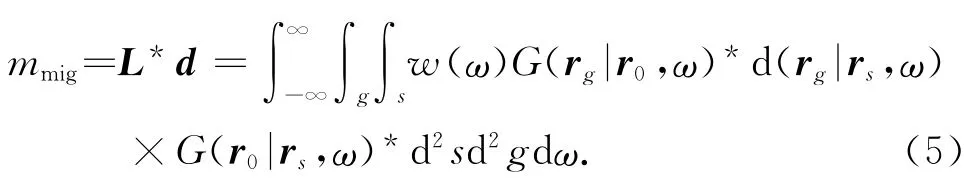
但由Born算子成像方程直接做偏移,成像效果较差,如采集脚印和偏移划弧现象很难消除,如图1b所示.因此需要对Born算子成像方程做改进.下面简单叙述一下两种改进方式:干涉偏移成像和偏移反演成像.
2.2 干涉偏移成像
在忽略仪器响应的情况下,地震检波器或地震仪记录到的地震信号等效于格林函数和地震子波的卷积.地震波干涉法的核心思想就是对记录的地震信号进行一定的数学处理,得到以其中一个检波器为震源的新的地震记录.如果对地震波场的格林函数进行运算后,能产生一个虚震源记录,那么在对地震子波做卷积之后,这种关系将仍然成立.因此,地震波干涉法的数学实现方式体现在虚拟震源格林函数的提取方法上[39].图2为关于VSP地震道干涉成像示意图.
对于震源在rs、检波器分别在rg1和rg2的数据d(rg1|rs)和d(rg2|rs),则可以定义它们的互相关公式为
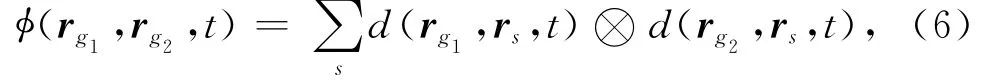
其中,φ(·)表示互相关.基于上述的互相关描述可以导出干涉偏移公式.设格林函数G(r0|rA)和G(r0|rB)分别满足相应的Helmholtz方程,对于VSP几何成像,在远场假设条件下,根据互易原理,He等[4]导出了干涉偏移成像公式:
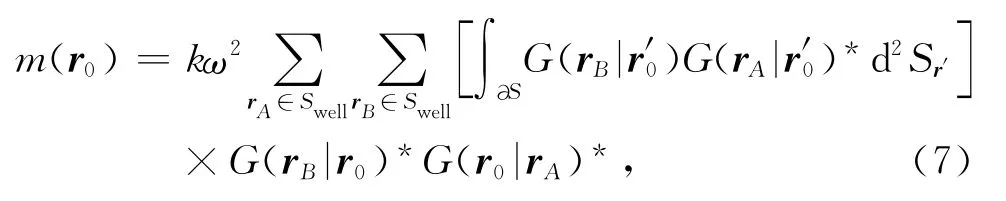
其中,Swell表示 VSP测井,G(r0|rA)*表示G(r0|rA)的复共轭,rB,rA∉∂S.按照互相关的定义,可定义
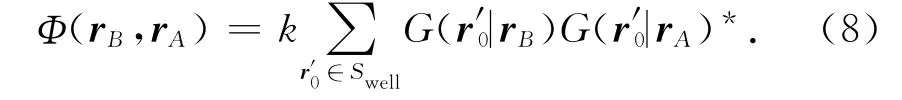
(8)式可以看做是虚拟震源在A点,由在B点的检波器记录得到的地震道记录.因此,公式(7)表明干涉偏移其实是对互相关得到的新的地震记录做偏移.
2.3 偏移反演成像
与干涉偏移不同的是,偏移反演成像的目的就是通过对偏移Green核函数和偏移图像作反卷积获得地球深部反射模型[15,17,22].但二者的共同目的是提高地震成像的分辨率.由第2.1节的Born近似,可得记录和反演合成地震数据按以下步骤实现:
(1)给定接收器和源以及点扩散模型m;
(2)计算点扩散响应d=Lm;
(3)偏移成像mmig=L*d=L*Lm;
(4)反演计算:
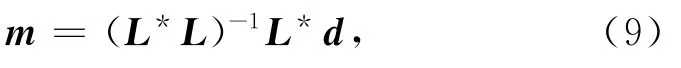
其中,L*定义作L的伴随算子.
按照 Yilmaz的思想[40],偏移反演需要计算(L*L)-1L*d.直接求逆不可取,因此计算实现上转化为求解一个偏移改变量能量最低的最小二乘问题
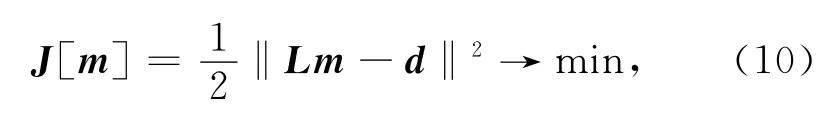
或
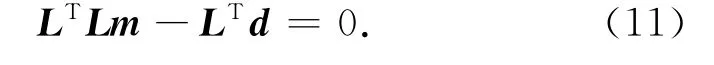
对于上述半正定的线性系统,有很多算法,比如利用改进的Cholesky分解法[17].但是,该计算方法只是在中等规模的问题时可以利用,因为其计算量可以达到O(1/6n3),这里n为变量的长度.对于大规模的偏移反演计算,现实可行的方法应该是迭代法.比如对于最小二乘偏移反演的迭代实现,Nemeth等[15]和Sjøberg等[16]采用了共轭梯度方法,其中的计算量主要集中在矩阵-向量积的计算上.但该方法由于共轭下降算法线性收敛速度的限制以及二次终止特性,将会导致计算时间漫长,从而影响了成像的分辨率和振幅的保真度,因此有必要研究一些改进措施.有关近期偏移成像振幅补偿和偏移反演成像算法的研究工作可见文献[14-16,18,22-25,41-44].
3 干涉偏移成像的数值实现
Yu和 Schuster以 及 He等[4,12,13]考 虑 了 干 涉偏移公式(7)的数值实现问题.记Φ(rg1,rg2,ω)为φ(rg1,rg2,t)的频率域表示,则对互相关的地震道φ(rg1,rg2,t)做偏移并对所有的位置rg1和rg2做叠加可得偏移公式:
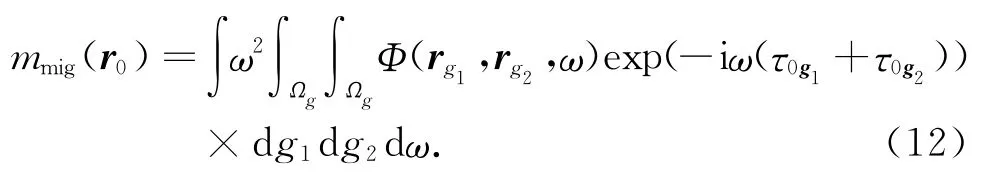
其中,τAB指的是波从A点传播到B点的走时.从上式可以看出,干涉偏移并不需要计算从震源到检波器的走时,但需要计算从虚拟震源到反射点的走时,对于三维偏移来说计算量巨大.He等[4]考虑了(12)式的经济型实现方式.数值上,上述积分可以做如下实现
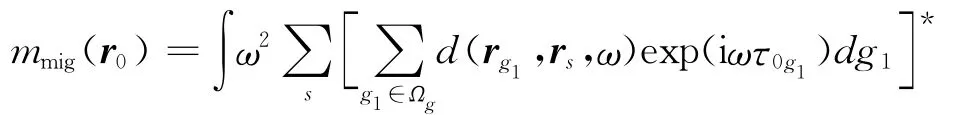

干涉偏移的好处是可以利用表面多次波成像,从而展宽成像区域提高分辨率.具体计算过程如下:
(1)分解垂直地震剖面数据为上行波dup和下行波ddown;
(2)通过滤波获得直达波ddirect,下行波ddown减去直达波ddirect得到多次波dmultiple;
(3)对直达波和多次波做互相关得到虚拟的地表地震剖面数据Φ;
(4)对上述的虚拟地表地震剖面数据Φ做偏移.
4 偏移反演成像的迭代正则化
4.1 正则化模型
正则化方法指的是寻找一族正则算子Rα(L,d)使得理论上观测数据d的噪声或误差水平趋于0时,Rα(L,d)收敛于能够求出的真实的地层反射模型m.Tikhonov标准正则化指的是求解一个极小化的正则泛函[17,34,45-46]:
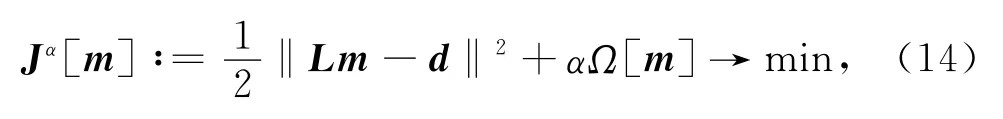
其中,Ω[·]为Tikhonov稳定子;α∈ (0,1)为可调节的正则参数,用于平衡不稳定性及光滑性.Ω[m]由用户根据问题的需要设定.如果Ω[m]为其中D为离散的对称正半定算子,表征对模型m施加的先验约束,则Rα(L,·)具有如下形式:
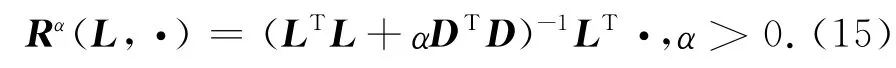
则地层反射模型m可以通过

得到.对于上述的非线性规划问题(14)式,有很多算法可以用来求解[17,34].但对于地震偏移反演成像来说,直接求逆计算量巨大,有必要研究合适可行的优化算法.我们研究迭代正则化方法,其迭代形式如下:
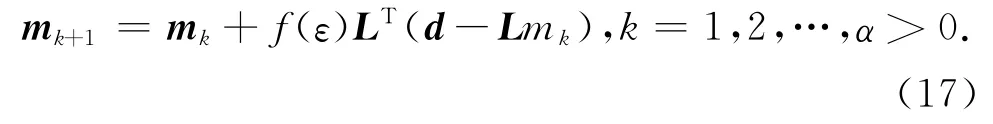
若f(ε)恒为 ( 0,1/‖LTL‖)中的常数,则对应着Landweber-Fridman迭代法;若f(ε)=argminJα(mkεεrk),其中rk=LTLmk-LTd,则对应着最速下降法[17,34].很明显,若令初始猜测值m0=0,并令k=1,f(ε)≡1,则一步梯度迭代法或一步Landweber-Fridman迭代法就是习惯上经常采用的Kirchhoff时间偏移公式.熟知一步梯度迭代法或一步Landweber-Fridman迭代法远远没有达到收敛的精度,因此直接的偏移会导致成像分辨率降低以及振幅恢复不准的缺点[18].
4.2 预条件共轭梯度迭代方法
下面给出选取正则算子Rα(L,·)的预条件形式.文献[25]探讨了一系列地震信号反演中梯度法的预条件问题.这里导出简单梯度迭代法和共轭梯度迭代法的预条件正则化公式.设P是一个对称正定矩阵,则条件数cond(P-1LTL)<cond(LTL)且P-1LTL的谱分布将比LTL的谱分布更集中.令C为一个非奇异矩阵,并定义分解式P=CCT.注意到公式(14)等价于极小化下面的一个二次规划问题[47]
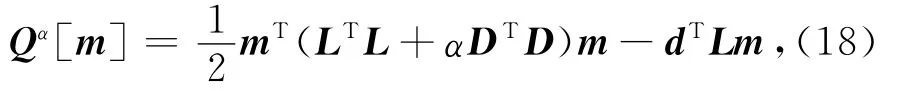
于是预条件问题可以写成
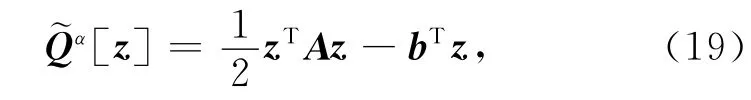
其中,A=C-1(LTL+αDTD)C-T,b=C-1LTd,z=CTm.Qα[m]和的梯度分别由下式算得

于是预条件的最速下降梯度迭代法可以写成:
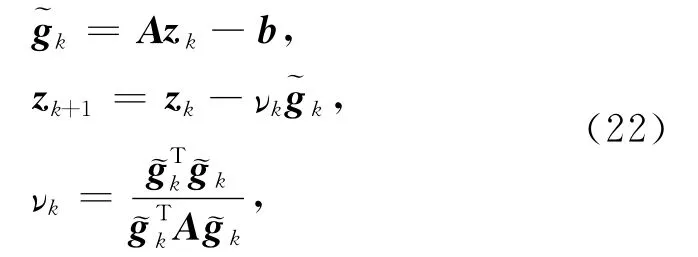
直接计算可得:
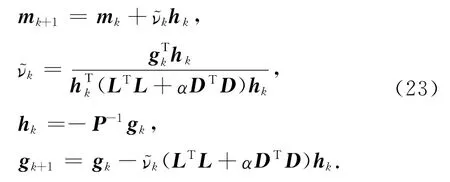
共轭梯度法具有二次终止性和较好的稳定性,该方法比最速下降方法稍微复杂一点.与最速下降方法不同的是,该方法在每个迭代步不必均采用最速下降方向,而考虑一个共轭方向hk-1.即如下的迭代公式:
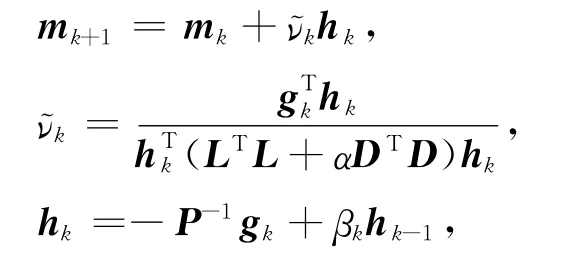
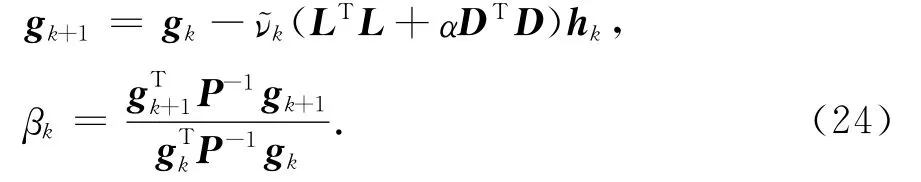
其中,gk为第k次迭代的梯度,即gk=LT(Lmk-d)+αDTDmk;hk为搜索方向;参数βk为共轭方向参数因子;νk为步长因子.在本文的计算中,预条件矩阵P取为对称矩阵LTL的逆的逼近.
4.3 共轭方向参数因子的优化选取
上述共轭方向参数因子βk的选取是基于Fletcher-Reeves(FR)方法,但FR方法并不是数值表现最好的.记ηk为搜索方向hk与负梯度方向-gk之间的夹角,并令预条件矩阵为单位阵,则cos(ηk)=当搜索方向与负梯度方向-gk之间的夹角ηk接近π/2时,则算法产生的步长可能非常小,导致算法表现变差.为此,我们考虑PRP方法,即选取参数因子βk为
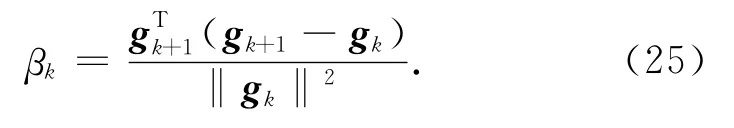
当搜索方向与负梯度方向之间的夹角ηk接近π/2并且迭代步长非常小以及 ‖gk+1-gk‖ < ‖gk‖时,则有可知下一次迭代的搜索方向将靠近负梯度方向-gk+1,从而避免了步长非常小的情况.考虑到预条件的情形,参数因子βk可以取为由于共轭梯度法产生共轭单调下降方向,该方向可能偏离目标值.因此,在多次迭代时,我们可以考虑重开始技巧,即对所有的k取β*k=max{βk,0},其中βk可以为FR的或PRP的.
5 数值模拟
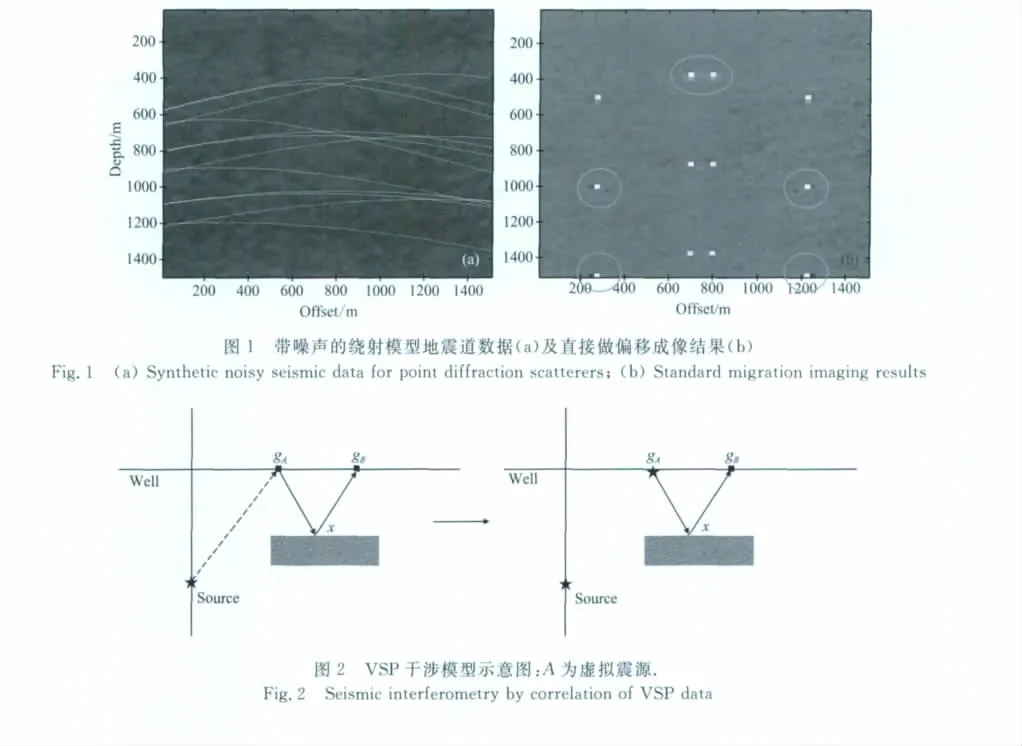
5.1 绕射点模型直接偏移成像及偏移反演成像对比
为了验证偏移反演算法在提高成像分辨率和振幅恢复方面的能力,我们进行数值试验.由于d为观测值,因此不可避免地带有各种噪声,假定该噪声具有可加性,则
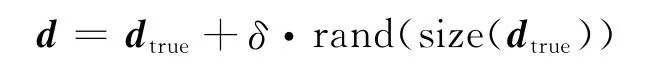
其中,δ为 (0,1)区间的噪声水平,rand(size(dtrue))具有与dtrue维数一致的Gauss随机噪声.dtrue由计算机做正向模拟生成.在本次试验中,我们取噪声水平δ为0.05.在构造正则算子Rα(L,d)时,需要选取正则参数.注意到如果α远远大于1,则将导致逼近问题对原问题过于光滑,从而计算结果与原问题的解相差甚远;相反,如果α远远小于1,则逼近问题未能将算子的谱做很好的改良,因而增加了误差/噪声的传播[34,48].在本次试验中,我们先验的选取α,即于区间(0,1)中取定一个合适的α值,且α>δ2,这样算法是可以保证稳定收敛的[48].设地下埋深有12个绕射散射点,采用56炮叠加,地震记录如图1a所示.直接的偏移成像结果见图1b.由图1b可以看出,直接的偏移对噪声控制能力差,成像分辨率质量不高.接着用正则化偏移反演进行计算.在预条件梯度迭代正则化偏移反演中,在噪声水平为0.05的情况下,采用如下的初始参数设置:初始模型赋零向量,正则参数取为α>δ2,正半定算子D取为单位矩阵,预条件矩阵取对称矩阵LTL的逆的逼近.成像的结果见图3a.同时画出了预条件共轭梯度迭代的误差分布,见图3b.为了验证正则偏移反演方法的振幅保真度明显好于标准的偏移算法,给出振幅对比如图4a和图4b.从图3和图4很明显看出,给出的预条件正则偏移反演方法具有快速的收敛性,只用了两次迭代则达到了很好的收敛效果.同时,很好地压制了噪声并且成像的分辨率和振幅的保真度要比标准的偏移成像结果好.
5.2 层速度模型干涉偏移成像及偏移反演成像对比
为了对比干涉偏移以及偏移反演算法在提高成像分辨率方面的能力,进行层速度模型VSP数据数值模拟.设一个5层速度模型,各层的厚度和速度是逐渐变化的,原始速度模型见图5a.在数据模拟中,取10个检波器放置在竖直井中,并进行80炮叠加;因为地震数据通常是带各种各样干扰的,因此我们取噪声水平δ为0.05进行随机干扰,获得图5b所示的原始地震记录.添加的噪声如图6a所示.

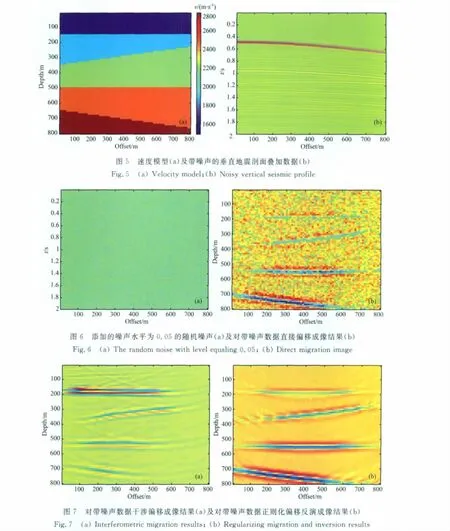
在预条件梯度迭代正则化偏移反演中,我们在噪声水平为0.05的情况下,采用如下的初始参数设置:初始模型赋零向量,正则参数取为α>δ2,正半定算子D取为单位矩阵,预条件矩阵取对称矩阵LTL的逆的逼近.标准的偏移成像结果见图6b.由图6b可以看出,直接的偏移对噪声控制能力差,成像分辨率质量不高.接着分别用干涉偏移方法和预条件正则化偏移反演进行计算,成像的结果分别见图7a和图7b.很明显干涉偏移和正则偏移反演方法很好地压制了噪声,成像的分辨率要比标准的偏移成像结果好.对比图7a和图7b发现,尽管干涉偏移和正则化偏移反演均能展宽成像区域并提高成像的分辨率,但后者似乎能够提供更宽的成像区域和更高的成像分辨率,而前者对噪声的压制要更高一些.
6 结 语
最近几十年Kirchhoff偏移在工业界得到了广泛的应用.但随着计算技术的进步以及应用的需求,更高质量的偏移成像需求越来越高.本文比较了直接的偏移、正则化偏移反演和干涉偏移三种方法的成像能力对比.特别是提出了预条件的梯度迭代正则化偏移反演方法.数值试验中,采用了带随机噪声的模拟地震剖面.数值模拟表明,干涉偏移和正则化偏移反演均能很好地控制噪声传播,成像效果较直接的偏移具有更好的分辨率,因此为这两种方法更广泛的应用提供了有希望的前景.
致 谢 感谢两位审稿人对论文的内容和格式上提出的良好建议.
(References)
[1]Claerbout J.Synthesis of a layered medium from its acoustic transmission response.Geophysics,1968,33(2):264-269.
[2]Bakulin A,Calvert R.Virtual source:New method for imaging and 4Dbelow complex overburden.74th Annual International Meeting,SEG,Expanded Abstracts,2004:2477-2480.
[3]常旭,刘伊克,王辉等.地震相干偏移与数据自参照偏移的关系.地球物理学报,2009,52(11):2840-2845.Chang X,Liu Y K,Wang H,et al.Seismic interferometric migration and data-referenced-only migration.Chinese J.Geophys.(in Chinese),2009,52(11):2840-2845.
[4]He R Q, Hornby B,Schuster G.3Dwave-equation interferometric migration of VSP free-surface multiples.Geophysics,2007,72(5):S195-S203.
[5]Schuster G T,Yu J,Sheng J,Rickett J.Interferometric/daylight seismic imaging.Geophysical Journal International,2004,157(2):838-852.
[6]Schuster G T,Katz L,Followill F,et al.Autocorrelogram migration:Theory.Geophysics,2003,68(5):1685-1694.
[7]Snieder R,Grêt A,Douma H,et al.Coda wave interferometry for estimating nonlinear behavior in seismic velocity.Science,2002,295(5563):2253-2255.
[8]Wang Y B,Luo Y,Schuster G T.Interferometric interpolation of missing seismic data.Geophysics,2009,74(3):SI37-SI45.
[9]Wapenaar K.Retrieving the elastodynamic Green′s function of an arbitrary inhomogeneous medium by cross correlation.Physics Review Letters,2004,93(25):254301-1-254301-4.
[10]Wapenaar K,Draganov D,Robertsson J O A,et al.Seismic Interferometry:History and Present Status.Geophysics Reprint Series No.26,Society of Exploration Geophysicists,2008.
[11]Wapenaar K,Fokkema J.Green′s function representations for seismic interferometry.Geophysics,2006,71(4):SI33-SI46.
[12]Yu J H,Katz L,Followill F,et al.Autocorrelogram migration:IVSPWD test.Geophysics,2003,68(1):297-307.
[13]Yu J H,Schuster G T.Crosscorrelogram migration of inverse vertical seismic profile data.Geophysics,2006,71(1):S1-S11.
[14]Hu J X,Schuster G T,Valasek P A.Poststack migration deconvolution.Geophysics,2001,66(3):939-952.
[15]Nemeth T,Wu C J,Schuster G T.Least-squares migration of incomplete reflection data.Geophysics,1999,64(1):208-221.
[16]Sjøberg T A,Gelius L J,Lecomte I.2Ddeconvolution of seismic image blur.Expanded Abstracts,SEG 73th Annual Meeting,Dallas,2003.
[17]王彦飞,斯捷潘诺娃I E,提塔连科V N等.地球物理数值反演问题[全球变化与地球系统科学系列].北京:高等教育出版社,2011.Wang Y F,Stepanova I E,Titarenko V N,et al.Inverse Problems in Geophysics and Solution Methods[Series in Global Change and Earth System Science].Beijing:Higher Education Press,2011.
[18]Wang Y F,Yang C C.Accelerating migration deconvolution using a non-monotone gradient method.Geophysics,2010,75(4):S131-S137.
[19]Aki K,Richards P G.Quantitative Seismology:Theory and Methods.San Francisco:W H Freeman and Company,1980.
[20]Claerbout J F.Imaging the Earth′s Interior.Oxford:Blackwell,1985.
[21]Stolt R H,Benson A K.Seismic Migration:Theory and Practice,Vol.5,Handbook of Geophysical Exploration,Section I.Seismic Exploration.London:Geophysical Press,1986.
[22]Lecomte I.Resolution and illumination analyses in PSDM:A ray-based approach.The Leading Edge,2008,27(5):650-663.
[23]Guitton A.Amplitude and kinematic corrections of migrated images for nonunitary imaging operators.Geophysics,2004,69(4):1017-1024.
[24]Sacchi M D,Wang J,Kuehl H.Regularized migration/inversion:new generation of imaging algorithms.CSEG Recorder,2006,31(S1):54-59.
[25]Wang Y F.Preconditioning non-monotone gradient method for retrieval of seismic reflection signals.Advances in Computational Mathematics,2012,36(2):353-376.
[26]Marquardt D W.An algorithm for least-squares estimation of nonlinear parameters.SIAM J.Appl.Math.,1963,11(2):431-441.
[27]Levenberg K.A method for the solution of certain nonlinear problems in least squares.Quart.Appl.Math.,1944,2:164-166.
[28]崔岩,王彦飞,杨长春.带先验知识的波阻抗反演正则化方法研究.地球物理学报,2009,52(8):2135-2141.Cui Y,Wang Y F,Yang C C.Regularizing method with a priori knowledge for seismic impedance inversion.Chinese J.Geophys.(in Chinese),2009,52(8):2135-2141.
[29]李振华,王彦飞,杨长春.正则化偏移成像的全局优化快速算法.地球物理学报,2011,54(3):828-834.Li Z H,Wang Y F,Yang C C.A fast global optimization algorithm for regularized migration imaging.Chinese J.Geophys.(in Chinese),2011,54(3):828-834.
[30]Wang Y F,Yuan Y X.Convergence and regularity of trust region methods for nonlinear ill-posed inverse problems.Inverse Problems,2005,21(3):821-838.
[31]Tarantola A.Inverse Problems Theory:Methods for Data Fitting and Model Parameter Estimation.Amsterdam:Elsevier,1987.
[32]Ulrych T J,Sacchi M D,Woodbury A.A Bayesian tour to inversion.Geophysics,2000,66:55-69.
[33]杨文采.地球物理反演和地震层析成像.北京:地质出版社,1989.Yang W C.Geophysical Inversion and Seismic Tomography(in Chinese).Beijing:Geological Publishing House,1989.
[34]王彦飞.反演问题的计算方法及其应用[当代科学前沿论丛].北京:高等教育出版社,2007.Wang Y F.Computational Methods for Inverse Problems and Their Applications[New Frontiers of Sciences](in Chinese).Beijing:Higher Education Press,2007.
[35]Nolet G.Solving or resolving inadequate and noisy tomographic systems.J.Comp.Phys.,1985,61(3):463-482.
[36]Nolet G,Snieder R.Solving large linear inverse problems by projection.Geophys.J.Int.,1990,103(2):565-568.
[37]VanDecar J C,Snieder R.Obtaining smooth solutions to large,linear,inverse problems.Geophysics,1994,59(5):818-829.
[38]Trampert J,Leveque J J.Simultaneous iterative reconstruction technique:physical interpretation based on the generalized least squares solution.Journal of Geophysical Research,1990,95(B9):12553-12559.
[39]陶毅,符力耘,孙伟家等.地震波干涉法研究进展综述.地球物理学进展,2010,25(5):1775-1784.Tao Y,Fu L Y,Sun W J,et al.A review of seismic interferometry.Progress in Geophysics(in Chinese),2010,25(5):1775-1784.
[40]Yilmaz O.Seismic Data Analysis.Investigations in Geophysics No.10.Society of Exploration Geophysicists,Tulsa,Okla,2001.
[41]Chen J,Schuster G T.Resolution limits of migrated images.Geophysics,1999,64(4):1046-1053.
[42]Schuster G T.Green′s functions for migration.Abstracts of Expanded Abstracts 67th SEG meeting,1997:1754-1758.
[43]Schuster G T,Hu J X.Green′s function for migration:Continuous recording geometry.Geophysics,2000,65(1):167-175.
[44]Yu J H,Hu J X,Schuster G T,Estill R.Prestack migration deconvolution.Geophysics,2006,71(2):S53-S62.
[45]Tikhonov A N, Arsenin V Y.Solutions of Ill-posed Problems.New York:John Wiley and Sons,1977.
[46]Engl H W,Hanke M,Neubauer A.Regularization of Inverse Problems.Dorcrecht:Kluwer Academic Publishers,1996.
[47]袁亚湘.非线性规划数值方法.上海:上海科学与技术出版社,1993.Yuan Y X.Numerical Methods for Nonlinear Programming(in Chinese).Shanghai:Shanghai Science and Technology Press,1993.
[48]肖庭延,于慎根,王彦飞.反问题的数值解法[计算方法丛书].北京:科学出版社,2003.Xiao Y F,Yu S G,Wang Y F.Numerical Methods for the Solution of Inverse Problems[Series in Numerical Methods](in Chinese).Beijing:Science Press,2003.

