P波和S波接收函数的贝叶斯联合反演
王 峻,刘启元
1 中国地震局地质研究所 地 震动力学国家重点实验室,北京 100029
2 中国地震局地震预测研究所,北京 100036
1 引 言
自1979年Langston[1]提出长周期远震P波的等效震源假定以来,P波接收函数方法在研究地壳上地幔速度结构中得到了迅速发展和日益广泛的应用.但是,已有的理论及实际研究表明[2],P波接收函数(P-RF)反演得到的地壳上地幔S波速度结构限于80~100km深度范围.Farra和 Vinnik[3]曾率先发表了S波接收函数(S-RF)的研究结果.由于S波接收函数中岩石圈底部Sp转换波震相不受地壳多次波的干扰,S波接收函数在岩石圈-软流圈(LAB)边界研究中得到了广泛应用,显示了S波接收函数在探测岩石圈结构方面的优势[4-6].由于缺少相应的速度结构,S波接收函数偏移叠加中的时间-深度转换限于采用全球标准速度模型.Vinnik等[7]发展了S波接收函数反演的模拟退火方法,并结合P波接收函数进一步确定反演的结果.
数值检验表明[8],接收函数仅对地壳介质的相对速度结构(或波阻抗)较为敏感,其反演结果依赖于初始模型.Wu等[9]认为,采取恰当的反演方法并非不能根据P波接收函数正确地估计地壳的速度结构.但是,由于S波接收函数的优势频率限于0.2Hz左右,其反演结果依赖初始模型的问题难以避免.
实际上,反问题的本质决定了地球物理反演必然存在某种程度的不确定性.减少反演非唯一性的出路在于尽可能减小模型参数的自由度[10-11].为此,本文在刘启元等[2]发展的P波接收函数非线性复谱比反演方法的基础上,进一步实现P波和S波接收函数的联合反演,以便同时获取岩石圈深度范围内的P波与S波速度结构.
2 S波接收函数
2.1 S波接收函数的特征
Yuan等[12]曾计算过S波接收函数理论地震图的波场特征.其结果表明,岩石圈底部的转换震相SLP只能在震中距大于60°时才能观测到,并指出由于实际地球介质中横向非均匀效应,实际能够观测到SLP转换震相的震中距范围为55°~85°,而且当震中距大于85°时,SKS将先于S波到达,以至于大于这个震中距范围的观测数据不适合S波接收函数研究.理论研究还表明[12-13],SMP和SLP震相的极性相反,转换系数(绝对值)随震中距增大而减小.
岩石圈间断面很可能不是一个简单界面.考虑具有梯度带结构的LAB界面上的SLP转换震相特征是必要的.为了对S波接收函数中的SP转换震相有更深入的认识,利用震源区和接收区速度结构不同的矩阵-射线方法[14],我们计算了S波接收函数中SLP震相与LAB速度结构的关系.
图1(a,b)分别给出了当岩石圈间断面为简单界面和梯度带结构时的S波接收函数合成理论地震图.结果表明,相比梯度带结构,一阶间断面形态的LAB对形成较强的SLP震相有利.图1c给出了接收区近地表具有4km厚沉积层的情况,表明S波初至震相被基底面转换震相所掩盖,SLP震相的振幅明显相对增强,这与P波接收函数类似[15].图1d给出了震中距范围65°~80°的S波接收函数及其叠加的计算结果,表明震中距65°~80°范围内的S波接收函数具有较好的相干特征,其叠加结果使接收区各个界面上生成的转换震相均得到相应加强.对于更大的震中距范围(图1a),由于S波接收函数相干特征变差,它们的叠加结果将导致S波接收函数的波形畸变.
2.2 S波接收函数估计
图2分别给出了对单台复谱域最大或然性反褶积方法(MLD)[2],三分量接收函数的最大或然性反褶积方法(MMLD)[16-17]以及单台时间域迭代反褶积方法(ITD)[18]分离S波接收函数所作的数值检验.数值检验所用的远震数据(图2(b,c))采用震源区和接收区速度结构不同的矩阵-射线方法计算得到[14].对比图2(d,e,f)可见,上述三种方法在相当程度上都能还原S波接收函数垂直分量的理论波形。由于避免了使用等效震源假定,MMLD方法(图2f)能够更可靠地估计S波接收函数.需要指出的是,这仅是多道最大或然性三分量接收函数反褶积方法的一种特例,即我们只根据多个台站记录到的单个远震事件分离三分量接收函数,而三分量接收函数多道最大或然性反褶积方法要求在某个范围内的一个事件阵的数据[16-17].我们的检验结果表明,这对于避免等效震源假定仍然是有效的.本文将采用这个方法获得S波接收函数的估计.
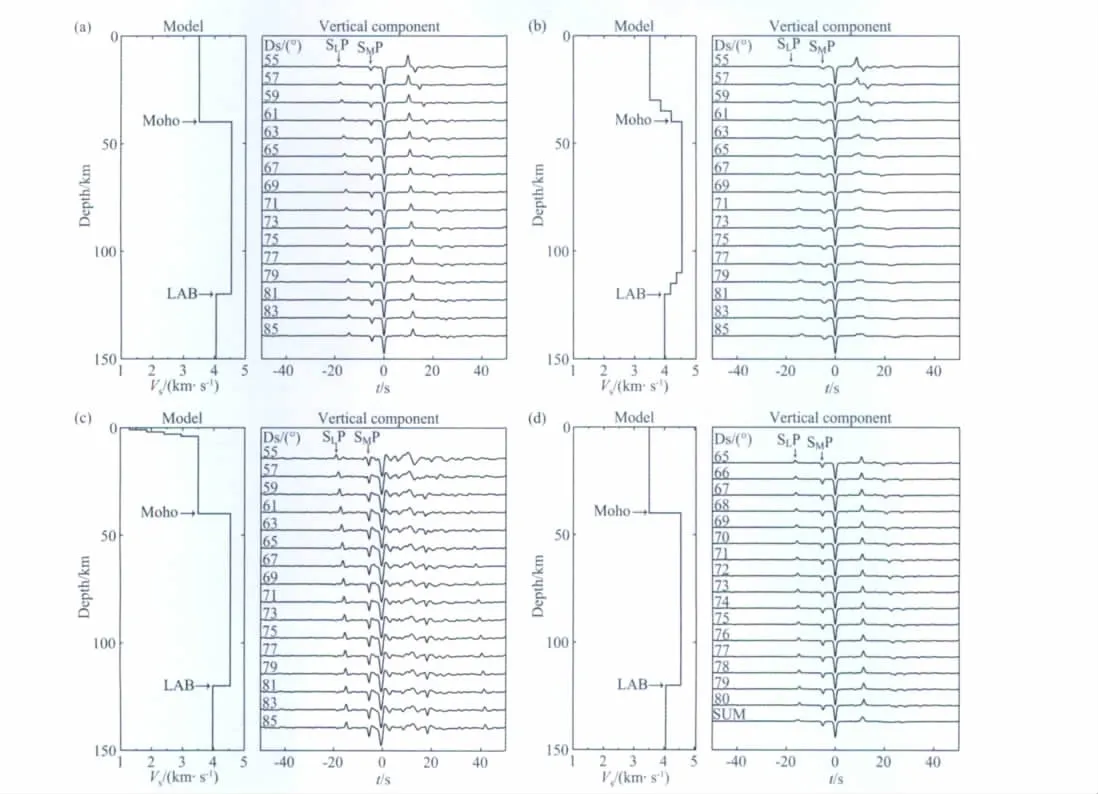
图1 S波接收函数理论地震图(a)岩石圈底部边界为简单界面;(b)岩石圈底部边界为梯度层;(c)近地表存在4km厚沉积层;(d)震中距65°~80°的S波接收函数叠加.各子图的左侧为接收区模型,右侧为相应的接收函数垂直分量(按径向分量的最大值归一).震源深度均为20km.Ds表示震中距.接收区以外的地球模型采用PREM模型.Fig.1 Synthetic S-receiver functions(a)LAB with first-order discontinuity;(b)LAB with gradient discontinuity;(c)4km thick sediment near the surface;(d)S-receiver function summed over distances 65°~80°.In the left side of each subfigure is the receiver model.In the right side of each subfigure is the vertical component of the S-receiver function normalized by the maximal amplitude of the radial component.Focal depths in computationsare 20km.Ds denotes the epicenter distance.The PREM model is taken as the earth model outside of the receiver area.
2003年4月—2004年9月,中国地震局地质研究所地震动力学国家重点实验室曾横跨天山布设了60个观测台站组成的流动宽频带地震台阵[19].作为一个例子,图3给出了其中部分台站的位置.图4给出了相应的S波及采用MMLD方法得到的相应S波接收函数的垂向及径向分量.零时刻相应于S波的初至.
3 P波和S波接收函数的联合反演
就接收函数反演而言,P波与S波接收函数具有各自的优势和局限性:(1)P波接收函数的优势频率约为1Hz,其模型空间的垂向分辨率为~2km;S波接收函数的优势频率约为0.2Hz,其模型空间的垂向分辨率为5~10km.(2)P波接收函数不利于探测深度超过80~100km 的速度结构变化[2,10],而S波接收函数在某种程度上可以弥补P波接收函数在这方面的不足.两者的结合可以实现高频和低频信息的互补及相互约束.
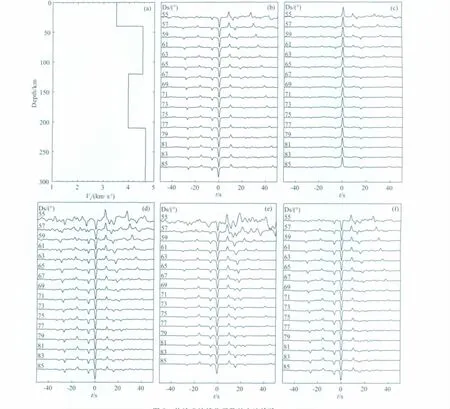
图2 估计S波接收函数的方法检验(a)接收区的S波速度模型;(b)S波接收函数的垂向分量;(c)S波接收函数的径向分量;(d)利用MLD方法估计的S波接收函数(垂直分量);(e)利用ITD方法估计的S波接收函数(垂直分量);(f)利用MMLD方法估计的S波接收函数(垂直分量).MMLD方法要求的多道观测数据来自介质参数相同,地壳厚度不同的远震合成S波波形数据.Ds:震中距.接收区以外的地球模型采用PREM模型.Fig.2 Numerical tests on the methods for isolating S wave receiver function(a)Receiver S-velocity model;(b)Vertical component of the S-receiver function;(c)Radial component of the S-receiver function;(d)Vertical component of S-receiver function estimated using MLD method;(e)Vertical component of S-receiver function estimated using the ITD method;(f)Vertical component of S-receiver function estimated using the MMLD method.The multiple-channel synthetic S waveforms generated by the crustal structure with same medium parameters,but different crustal thickness are taken as the data for testing the MMLD method.Ds denotes epicenter distance.The PREM model is taken as the earth model outside of the receiver.
虽然理论及实际研究已经表明[2,10],P波接收函数反演得到的地壳上地幔S波速度结构限于80~100km深度范围,但这并不意味P波接收函数不包含更大深度的上地幔速度结构的信息,只是这些信息被壳内混响的多次波掩盖,以至于仅靠P波接收函数反演难以提取相关的信息,并可能干扰对P波接收函数波形数据的正确解释.前人的结果表明[3-6],S波接收函数的探测深度可以达到岩石圈地幔.P波和S波接收函数的联合反演将弥补P波接收函数反演在探测深度方面的不足,并有助于避免把地幔速度结构的信息错误地归结为地壳的多次波.
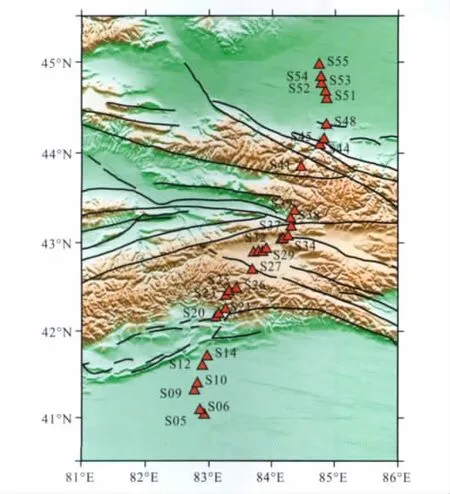
图3 横跨中国境内天山的台站分布红色三角形表示台站.S05-S55表示台站代码.Fig.3 Stations map across Chinese Tianshan The red triangles denote station.S05-S55denote the station code.
另外,P波接收函数主要对台站下方地壳上地幔的S波速度结构较为敏感,其反演的主要目标是解释其径向分量的波形[1-2,8].S波接收函数主要对台站下方地壳上地幔的P波速度结构较为敏感,其反演的主要目标是解释其垂向分量[7].但是,介质的P波和S波速度在物理上并非完全独立.泊松比表述了两者之间的内在联系.
对于P波接收函数非线性复谱比反演方法来说[2],其先验信息主要来自对地壳介质参数的一般认知.依据贝叶斯反演理论[20-21],P波与S波接收函数的联合反演可理解为把S波接收函数看作P波接收函数反演的先验信息,反之,也可以把P波接收函数看作对S波接收函数反演的惩罚约束.P波与S波接收函数的联合反演不但可以同时获取P波和S波速度参数,而且有助于两者的相互约束.
3.1 联合反演的算法
根据贝叶斯反演理论[20-21],模型空间的后验概率密度可以表示为
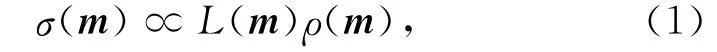
其中,L(m)称为或然性函数,它反映了模型预测结果与观测数据的拟合程度,ρ(m)为独立于观测数据的模型先验概率密度.在同时考虑P波接收函数与S波接收函数的情况下,我们有

和
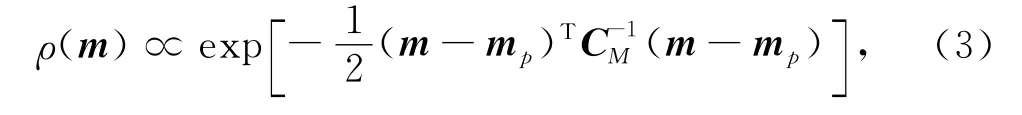
这里,g(m)为正演得到的合成地震图,d为观测数据矢量,m为模型参数矢量,*表示复共轭,T表示转置,而下标PR和SR分别表示P波和S波接收函数,下标p表示先验信息.CPR和CSR分别表示P波和S波接收函数的数据协方差矩阵.CM为先验模型的协方差矩阵.
根据式(2)和(3),我们可以得到相应的目标函数

反问题的求解意味着要求模型空间的后验概率密度σ(m)具有极大值,或者说需要寻求(4)式的极小值.为此目的,我们采用共轭梯度法.根据(4)式得到目标函数的梯度方向:
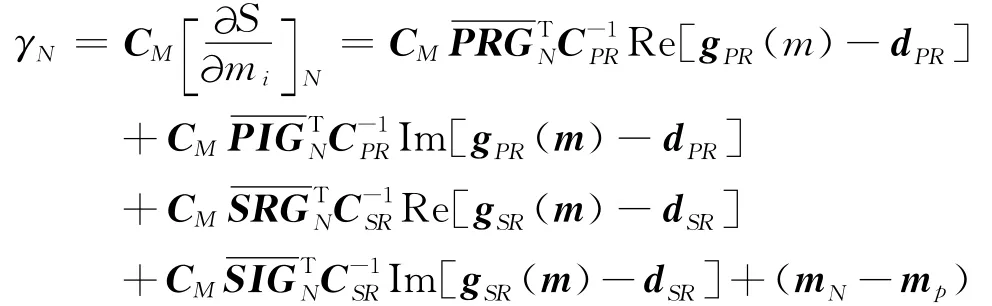
其中,
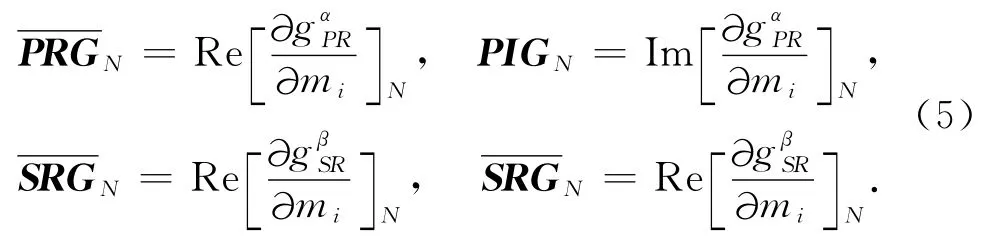
这里,Re表示实部,Im表示虚部,下标N表示第N次迭代,i=1,2,… ,l;α=1,2,… ,m;β=1,2,…,n.其中,l,m,n分别表示分层模型的层数,P波接收函数及S波接收函数的样点数.
P波和S波接收函数的正演采用Müller给出的反射率法[22].对于接收函数微分地震图的计算,我们采用Randall给出的方法[23].根据贝叶斯反演理论[20-21],可导出模型的后验协方差和模型空间解的分辨率
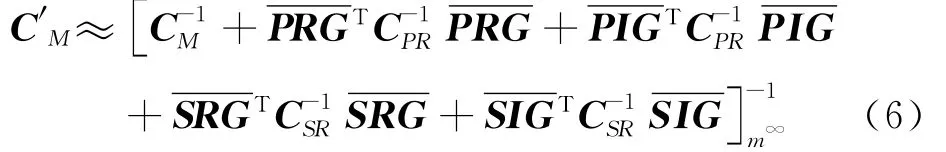
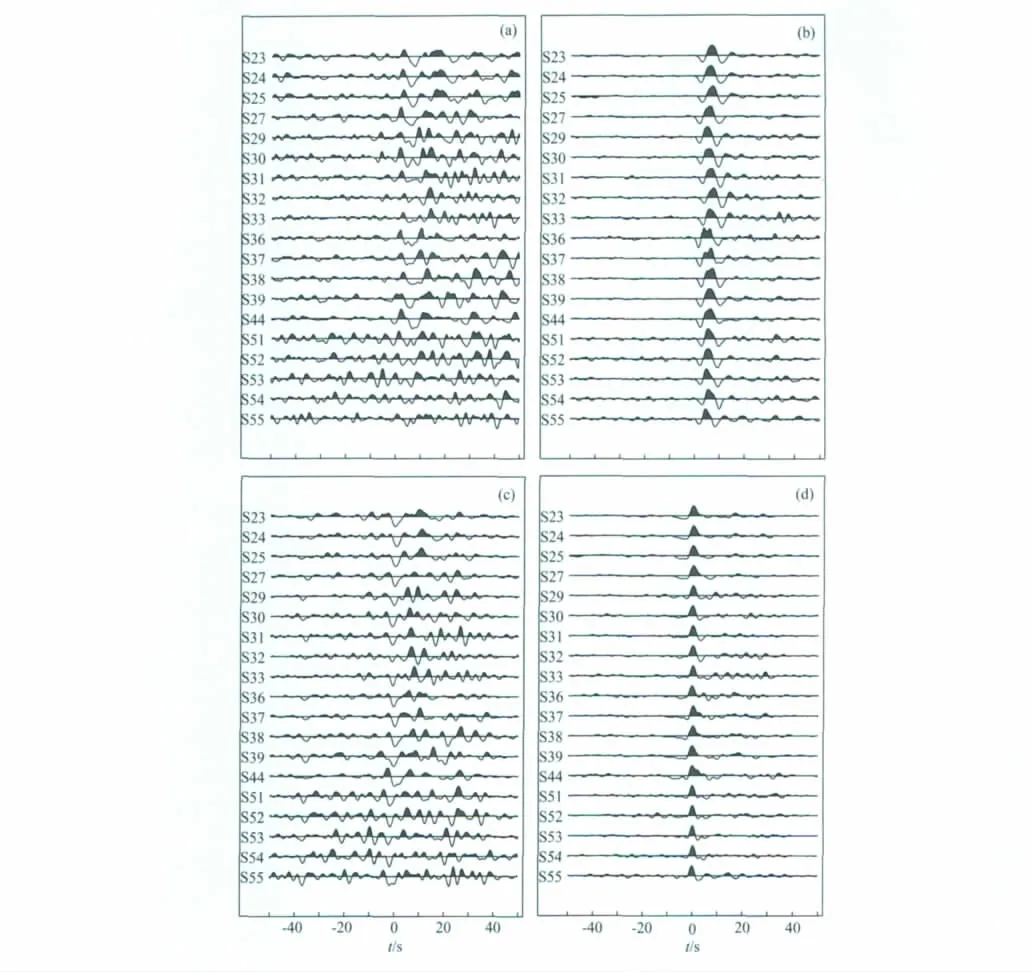
图4 横跨中国境内天山的S波接收函数(a)不同台站记录S波垂直分量;(b)不同台站记录S波的径向分量;(c)S波接收函数的垂直分量;(d)S波接收函数的径向分量.所用远震事件发震时刻:2003年7月21日13h53m58.49s.震级(Mw):6.4.震中位置:5.481°S,148.853°E.震源深度:189.6km.平均震中距:75.367°.平均台站方位角:111.653°.左侧为台站代码.数据处理:对远震事件的原始S波波形信号进行了低通滤波和重采样(5Hz),以便去除高频噪声;S波径向分量初至对齐,以便进行垂直分量叠加.Fig.3 S receiver function at the stations across Chinese Tianshan(a)Vertical component of S-waves;(b)NS component of S-waves;(c)Vertical component of S receiver functions;(d)Radial component of S receiver functions.Origin time:2003/07/21 13h53m58.49s.Magnitude(Mw):6.4.Location:5.481°S,148.853°E.Focal depth:189.6km.Epicenter distance averaged over stations:75.367°.Back azimuth averaged over stations:111.653°.The left side is the station code.Data processing:the original data of S-waves have been re-sampled after low-pass filtering.The sampling rate is 5Hz.The onsets of S-waves are aligned to sum all of traces.

这里,m∞表示模型空间中的最大或然性点,I为单位矩阵.
图5给出了本文联合反演算法的程序框图.对本文的联合反演算法,我们做以下几点简要说明:
(1)对于P波接收函数,我们引入了接收函数垂向分量与径向分量的初至振幅比.
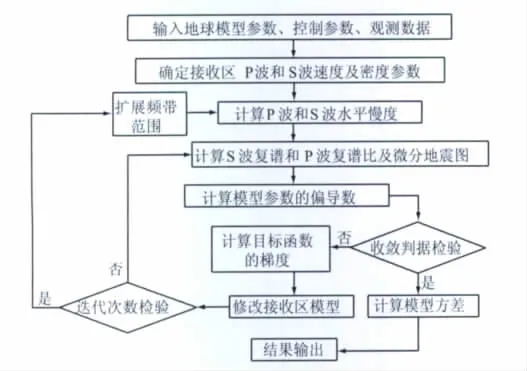
图5 P波与S波接收函数联合反演的流程图Fig.5 Diagram of the joint inversion of P-and S-receiver function
(2)P波与S波接收函数均采用逐步扩展的分频段反演,具体的频段分配见表1.理论和实际研究表明[2],接收函数反演包括1.0Hz以上的信息是必要的,缺少1.0Hz以上的短周期信息是不利于约束接收区的细结构.
(3)联合反演算法同时反演了P波和S波速度结构.通过限制接收区下方的地球介质的泊松比范围(0.2~0.35)有助于强化P波与S波速度参数的联系.
(4)反演收敛的判据主要依据P波与S波接收函数拟合的均方根误差.由于P波与S波振幅谱的量级不同,且它们的收敛速度也不协调,仿照文献[10],我们根据公式.
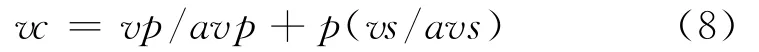
和

计算的总体方差的极小值作为收敛判据.这里,vp和vs分别表示P波和S波接收函数拟合的均方根误差,avp和avs分别表示P波和S波接收函数的观测振幅谱的算术平均.式(9)由迭代的初值给定.
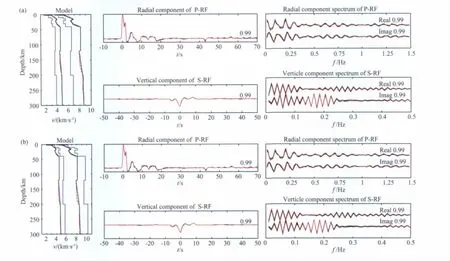
图6 P波与S波接收函数联合反演的数值检验左侧:接收区模型,其中黑色实线为“真实”模型,蓝色实线为初始模型,红色实线为反演得到的速度模型.中间:时间域接收函数拟合,红色实线:反演得到的接收函数;黑色实线:“真实”接收函数.右侧:复谱域接收函数拟合,黑色实线相应于“真实”接收函数的均方根误差范围,红色实线相应于反演得到的接收函数复谱.右边的数字为相关系数.Real:实部.Imag:虚部.Fig.6 Numerical test on the joint inversion of P-and S-receiver function Left:receiver model;black lines represent“true”model;red lines represent the inversion model;blue lines are the initial mode.Centre:waveform fitting of P-receiver functions(upper)and S-receiver functions(lower)in time domain;red solid lines are the results after inversion.Black solid lines are“true”receiver functions.Right:waveform fitting of P-receiver functions(upper)and S-receiver functions(lower)in complex spectrum domain.Black solid lines indicate the mean square deviations of the“true”receiver functions in complex spectrum domain.Red solid lines are the results after inversion in complex spectrum domain.The digits on the right are the correlation coefficients.
(5)虽然理论上利用预条件共轭梯度法可以加速反演的收敛[20-21],但当求解的问题具有很强的非线性时,预条件共轭梯度法很可能是不收敛的[2].
3.2 数值检验
图6给出了对本文方法所作的数值检验结果.由图6(a,b)可知,我们分别假定了两个远离“真实”模型的初始模型.它们的整体速度值偏离“真实”模型~20%.接收区以外的地球模型采用PREM模型.用于反演的数据为“真实”模型的理论P波和S波接收函数,并假定震中距为70°,震源深度为20km.数据的观测误差假定为相应振幅谱最大值的1%.图6表明,在接收区300km深度的范围内,无论初始模型的速度参数高于或者低于“真实”模型,反演的结果都能够比较好地预测接收区的“真实”速度参数.

表1 P波与S波频段分配(Hz)Table 1 Frequency band of P-and S-receiver fucuion(Hz)
3.3 反演实例
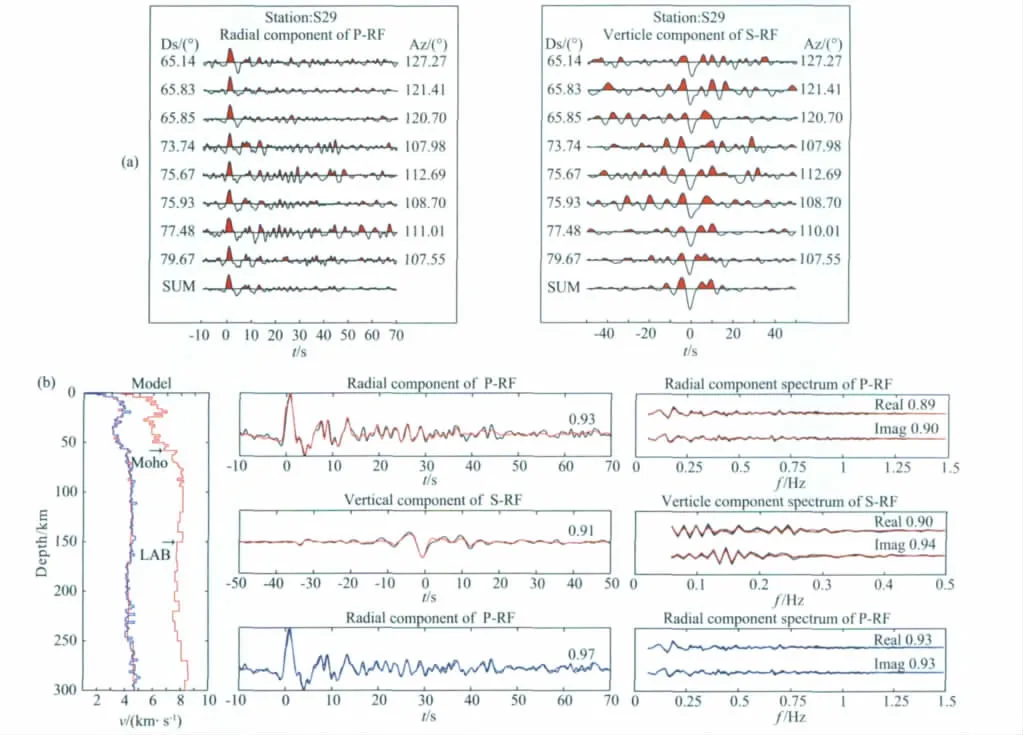
图7 反演实例:中国境内天山的地壳上地幔速度结构(a)P波接收函数的径向分量(左图)和S波接收函数的垂直分量(右图);Ds表示震中距.Az表示台站方位角;(b)P波和S波接收函数联合反演:左图:红色实线为联合反演得到的接收区P波和S波速度模型,蓝色实线为P波接收函数反演得到的S波速度模型;中图:联合反演得到的P波接收函数(上)和S波接收函数(中)及P波接收函数反演波形拟合(时间域);右图:联合反演得到的P波接收函数(上)和S波接收函数(中)及P波接收函数反演的波形拟合(复谱域).数据与预测结果的相关系数置于相应波形的右侧.Fig.7 Example:the velocity structure of the crust and upper mantle beneath Chinese Tianshan.(a)Radial component of P-receiver function(left)and the vertical component of S-receiver function(right);Ds denotes epicenter distance.Az denotes back azimuth;(b)Joint inversion of P-and S-receiver function:in the left is the P-and S-velocity model of the receiver by the joint inversion(blue color)and the S-velocity model of the receiver by the P-receiver function inversion(red color);in the center are the waveform fitting by the joint inversion of P- (upper)and S-receiver function(middle)as well as that by the P-receiver function inversion,respectively(time domain);in the right are the waveform fitting by joint inversion of P- (upper)and S-receiver function(middle)and P-receiver function inversion(lower),respectively(complex spectrum domain).The correlation coefficient is located in the right side of each waveform.
作为一个例子,图7分别给出了P波和S波接收函数联合反演及P波接收函数反演得到的天山宽频带流动地震台阵台站S29(图3)下方地壳上地幔P波和S波速度结构.两种反演的接收区初始模型均采用PREM模型.对于P波和S波接收函数联合反演,接收区地壳上地幔的模型分层:0~100km深度范围内,层厚为2km,100~300km深度范围内,层厚度为10km;对于P波接收函数反演,接收区地壳上地幔的0~300km深度范围内,层厚均为2km.图7a给出了用于反演的P波和S波接收函数.它们来自相同远震事件。实际经验表明,采用相同远震事件的P波与S波接收函数数据效果优于两者不同的情况.
图7b表明,(1)台站S29下方地壳厚度为58km,与前人P波接收函数反演得到的结果基本一致[24];(2)岩石圈底部边界为150km,这与S波接收函数偏移叠加研究给出的中天山岩石圈底部边界深度估计相近[5];(3)在220~270km 的深度上显示的梯度带结构可能是上地幔软流圈底部边界。
图7b的进一步分析可知,在0~100km深度范围内,联合反演给出的P波和S波速度结构基本上是协调一致的,联合反演和P波接收函数反演给出的S波速度结构基本上也是协调一致的.但在更大的深度上,情况并非如此.上述观察表明,P波接收函数主要对地壳及上地幔顶部的S波速度细结构比较敏感,而S波接收函数主要对P波速度结构的长周期分量比较敏感.因此,本文的联合反演方法对于大于100km深度上地幔的S波速度结构约束较弱.其结果主要反映的是P波接收函数提供的信息.与数值检验结果的差异是因为观测的P波接收函数低频分量相对不足.
4 结 论
本文在S波接收函数运动学及动力学特征研究和接收函数非线性复谱比反演方法的基础上[2],进一步发展了基于贝叶斯理论的P波和S波接收函数的非线性联合反演方法.根据本文的结果,我们可以得到以下主要结论:
(1)适用于S波接收函数反演的震中距范围约为55°~80°;为保证台站记录的S波有足够高的信噪比,用于S波接收函数反演的远震事件震级须大于5级.
(2)与陡变的岩石圈底部界面相比,梯度带类型LAB边界上生成的SLP转换波相对较弱;当台站下方近地表存在沉积盖层时,S波接收函数中SLP转换波的振幅将会增强.
(3)不依赖于等效震源假定的三分量接收函数多道最大或然性反褶积方法更适合S波接收函数的估计.
(4)数值检验结果表明,P波与S波接收函数联合反演可以同时提取地壳及岩石圈地幔的P波与S波速度结构;在初始模型速度参数偏离真实模型20%的情况下,能够对300km深度范围内的参数做出预测.
(5)利用本文方法对天山台阵台站观测的P波接收函数与S波接收函数的联合反演表明,该台站下方地壳厚度为58km,岩石圈底部边界为150km.致 谢 作者与陈九辉,郭飚,李昱,齐少华等的讨论使本文工作受益匪浅,在此表示感谢!
(References)
[1]Langston C A.Structure under Mount Rainier,Washington,inferred from teleseismic body waves.J.Geophys.Res.,1979,84(B9):4749-4762.
[2]刘启元,Kind R,李顺成.接收函数复谱比的最大或然性估计及非线性反演.地球物理学报,1996,39(4):502-513.Liu Q Y,Kind R,Li S C.Maximal likelihood estimation and nonlinear inversion of the complex receiver function spectrum ratio.Chinese J.Geophys.(in Chinese),1996,39(4):502-513.
[3]Farra V,Vinnik L.Upper mantle stratification by P and S receiver functions.Geophys.J.Int.,2000,141(3):699-712.
[4]Oreshin S,Vinnik L,Peregoudov D,et al.Lithosphere and asthenosphere of the Tien Shan imaged by S receiver functions.Geophys.Res.Lett.,2002,29(8):1191,doi:1029/2001GL014441.
[5]Kumar P,Yuan X,Kind R,et al.The lithosphereasthenosphere boundary in the Tien Shan-Karakoram region from S receiver functions:Evidence for continental subduction.Geophys.Res.Lett.,2005,32,L07305,doi:10.1029/2004GL022291,1-4.
[6]Soudoudi F,Yuan X,Liu Q Y,et al.Lithospheric thinkness beneath the Dabie Shan,central eastern China from S receiver functions.Geophys.J.Int.,2006,166(3):1363-1367.
[7]Vinnik L P,Reigber C,Aleshin I M,et al.Receiver function tomography of the central Tien Shan.Earth Planet.Sci.Lett.,2004,225(1-2):131-146.
[8]Ammon C J,Randall G,Zandt G.On the nonuniqueness of receiver function inversion.J.Geophys Res.,1990,95(B10):15303-15318.
[9]Wu Q,Li Y,Zhang R,et al.Wavelet modeling of broadband receiver functions.Geophys.J.Int.,2007,170(2):534-544.
[10]Liu Q Y,Li Y,Chen J H,et al.Joint inversion of receiver function and ambient noise based on Bayesian theory.Chin.J.Geophys.,2010,53(11):961-972.
[11]Scales J A,Snieder R.The anatomy of inverse problems.Geophysics,2000,65(6):1708-1710.
[12]Yuan X H,Kind R,Li X Q,et al.The S receiver functions:synthetics and data example.Geophys.J.Int.,2006,165(2):555-564.
[13]Aki K,Richards P G.Quantitative Seismology:Theory and Methods.San Francisco:W.H.Freeman and Company,1980,133-155.
[14]刘启元,范会吉.震源区和接收区结构不同情况下体波合成地震图的矩阵-射线方法.地球物理学报,1992,35(2):193-203.Liu Q Y,Fan H J.The ray-matrix method of synthetic seismograms for different source and receiver structure.Chinese J.Geophys.(in Chinese),1992,35(2):193-203.
[15]刘启元,邵学钟.天然地震PS转换波动力学特征的初步研究.地球物理学报,1985,28(3):291-302.Liu Q Y,Shao X Z.A study of the dynamic characteristics of PS converted waves with synthetic seismogram.Chinese J.Geophys.(in Chinese),1985,28(3):291-302.
[16]刘启元,Kind R.远震接收函数及非线性复谱波形反演.∥中国地球物理学会年刊.北京:地震出版社,1992,18.Liu Q Y,Kind R.Lithospheric receiver function and its nonlinear complex spectrum inversion.∥Annual of the Chinese Geophysical Society (in Chinese).Beijing:Seismological Press,1992,18.
[17]刘启元,KindR.分离三分量远震接收函数的多道最大或然性反褶积方法.地震地质,2004,26(3):416-425.Liu Q Y,Kind R.Multi-channel maximal likelihood deconvolution method for isolating 3-component teleseismic receiver function.Seismology and Geology (in Chinese),2004,26(3):416-425.
[18]Ligorria J P,Ammon C J.Iterative Deconvolution and Receiver-Function Estimation.Bull.Seism.Soc.Am.,1999,89(5):1395-1400.
[19]李顺成,刘启元,陈九辉等.横跨天山的宽频带流动地震台阵观测.地球物理学进展,2005,20(4):955-960.Li S C,Liu Q Y,Chen J H,et al.Passive broadband seismic array observation across Tianshan.Progress in Geophysics(in Chinese),2005,20(4):955-960.
[20]Tarantola A.Inversion Problem Theory,Method for Data Fitting and Model Parameter Estimation.Amsterdam:Elsevier,1987.
[21]Tarantola A.Inverse Problem Theory,and Methods for Model Parameter Estimation.SIAM,PA 19104-2688USA,2005.
[22]Müller G.The reflectivity method:a turtorial.J.Geophys.,1985,58(3):153-174.
[23]Randall G E.Efficient calculation of differential seismograms for lithospheric receiver functions.J.Geophys.Int.,1989,99(3):469-481.
[24]Li Y,Liu Q Y,Chen J H,et al.Shear wave velocity structure of the crust and upper mantle underneath the Tianshan orogenic belt.Science in China (Series D),2007,50(3):321-330.

