变化地磁场预测的支持向量机建模

易世华，刘代志，何元磊，齐 玮

第二炮兵工程大学，西安 710025

1 引 言

变化地磁场是地磁学和空间物理学等研究的重要内容，在很多应用研究领域都需要考虑变化地磁场的影响，如空间天气的监测和预报[1］、地震预报的地磁方法[2］、地磁导航与地磁寻的技术[3］等.随着应用研究的深入，对变化地磁场的精确建模与预测成为一项重要的研究课题.在地磁导航中，需要高精度、高时空分辨率的变化地磁场模型，用以消去磁场变化的影响.此外，变化磁场环境也是地球空间环境的重要组成部分，研究变化磁场模型在理论和实践中都有极为重要的意义[1，4-6］.

变化地磁场主要包括主磁场的长期变化和变化磁场的快速变化两种类型，分别有不同的物理起源和机制，受多种因素的制约和影响.长期变化是地球主磁场的一种长时间周期变化，在短期内通常表现为缓慢的趋势性变化；变化磁场主要起源于电离层和磁层电流体系（它们在地球内部的感应电流也有重要贡献），主要是由太阳风粒子和辐射引起，通常呈现出十分复杂的时间演化和空间分布特征[1］，难以用完备的理论模型精确描述.

虽然磁场变化具有十分复杂的特性，且包含一定的随机性成分，但也不是完全随机的，而是有一定周期性、相关性等规律性特点.通过把握这种规律性就可以对未来时刻的磁场值作出一定精度的预测，从而满足应用上的需求.随着非线性方法的发展，分形、混沌等理论也用于对变化磁场的分析研究[7-9］.结果表明，变化磁场具有混沌特性，其长期演化结果不可预测，但短期行为是可以预测的，采用合适的方法技术就可以实现对变化磁场的短期预测.文献[10-13］基于变化磁场观测数据开展了建模预测工作，但均没有以日地系统观点，综合空间和地面监测数据进行建模预测研究，而且建模的时间尺度基本上都以小时为主，远远满足不了辅助导航等对变化地磁场高精度高时空分辨率模型的需求.

观测和研究表明，地磁场在固体地球以外的空间分布，一方面取决于地球主磁场本身的强度和结构，另一方面取决于太阳风与行星际磁场的作用.具体来说，变化磁场与太阳、行星际空间、磁层、电离层中发生的一系列复杂现象有密切关系，所有这些现象从不同侧面反映了日地能量耦合过程的总体特点[1］.另一方面，从变化磁场的形态学研究可知，变化磁场的各种组分分别与太阳自转周、地球自转周、地球公转周、月球运转周等有密切关系.综上，我们可以将影响制约变化磁场的因素大致分为两类：一类是确定性的时间标度，即太阳自转周（地磁活动性巴特尔斯周变化）、地球自转周（磁场变化随地方时、世界时变化的部分）、地球公转周（季节变化），月球运转周（太阴日变化），以及随着时间推移的逐日变化、长期变化等；另一类是不确定的随时间变化的量，如太阳活动性（太阳黑子数、太阳射电流量、太阳风等参数）、磁层、电离层状态（电离层电子密度TEC等），以及地磁活动指数等.这些量在当前及过去时刻的值可由观测得到，在未来时刻的值需要借助其他预测手段得到，在此方面已有不少研究成果可供借鉴及应用[14-20］.未来某一时刻变化地磁场值，不仅与过去一定时间的磁场观测值有关，显然也与上述影响制约因素有关.可以认为，在太阳风和行星际磁场的作用下，地球磁场叠加上了一定的变量，经过一系列复杂过程，形成了若干时间以后的变化场值.

综上所述，为了实现对变化地磁场的高精度建模与预测，以物理起源为基础，按照日地系统观点，综合空间和地面监测数据，采用现代智能信号处理方法，构建变化场的经验综合模型将是一种好的研究思路.对磁场变化进行建模预测，实质上就是要采用数学手段表达其变化规律，建立映射关系模型.可以用不同方法构建此映射，从而发展出多种模型，包括统计回归、自适应滤波、灰色系统、神经网络、支持向量机等.由于支持向量机方法可以通过核函数实现从样本空间到高维特征空间的非线性映射，通过非线性映射，将低维空间中的非平稳过程映射到高维空间，是一种统计最优的技术，对于复杂的非线性系统，运用支持向量机方法能够更准确地对其进行建模预测[21-23］.本文采用求解较为简单的最小二乘支持向量回归机[24］对变化场进行建模预测.

2 支持向量机模型的建立和训练

2.1 建模算法

对于给定的训练集T= ｛（x1，y1），…，（xl，yl）｝，其中xi∈Rn，yi∈R，i=1，…，l，最小二乘支持向量回归机（Least squares support vector regression，LSSVR）[24］是寻求形如y=（w·x）+b的决策函数，用以推断任意输入x对应的输出y.其算法步骤为

（1）选取适当的核函数K（x，xi）和适当的参数C＞0；

（2）构造并求解二次规划

（4）构造决策函数

本文采用最常用的径向基核函数：K（x，xi）=exp｛-‖x-xi‖2／σ2｝，其中σ为核参数.在建模过程中，均采用交叉验证法选择最优的参数σ和C.

2.2 建模数据

地磁变化可以分为活动较为平静的时段和较为剧烈的时段，在活动剧烈时，磁场变化更为复杂多变，从地磁辅助导航等应用角度来说，也许我们不得不避开此时段.所以，建模与预测主要针对较为平静的时段，选用的数据为太阳活动与地磁活动较为平静的2009年全年的数据.该年Kp指数只有极个别大于5，其它均在5以下.具体为中国地磁台网乾陵台观测数据.根据文献[25-26］研究结果，Z分量是优良的匹配分量.所以，本文选用Z分量为建模预测对象，其它分量也可作类似处理.该台地理坐标为北纬34.570°、东经108.230°，海拔885m.本文选用的2009年地磁Kp指数、Dst指数、太阳黑子数、太阳射电流量、ACE卫星探测的太阳风速度、太阳风离子密度、行星际磁场南向分量等数据源自美国国家地球物理数据中心（http：∥www.ngdc.noaa.gov／）.

2.3 建模过程

在应用中，要求尽量提高变化地磁场序列的时间分辨率，但时间分辨率越高，计算量以及预测时长将会受到影响.综合考虑各种情况，同时在对变化地磁场序列各时间分辨率上的变化特性做统计分析的基础上，采用10min均值作为建模预测对象.在预测时长方面，结合应用需求，并根据文献[27］对Sq逐日变化的统计研究结果，即Sq的日变幅具有显著的逐日变化.可知，超过一天的预测将难以达到较高的精度.故此，预测时长最长为24h，以3h的短时预测为考察重点.

在建模过程中，首先直接采用地磁观测数据做训练和检测，依次以前一星期的数据做训练建立模型，后一星期的数据做预测检验（理论上用于建模的数据更长，将会有更好的结果.而在辅助导航中，希望能以较短的观测数据建立足够精度的变化场模型.权衡考虑，建模用数据长度选为1星期，后面建模中也同样如此）.以预测期为3h作标准，发现用前3点变化地磁场历史观测数据做建模时精度最高.因此，在模型输入中，地磁历史观测数据时间长度选定为3.在此基础上，输入向量依次增加其它各种影响制约因素.

考虑到日地系统是一个非常复杂的动力学系统，影响磁场变化的因素难以胜数，根据前人研究的结论[1，15］及所获数据的实际情况，选择了描述地磁活动性的Kp指数、Dst指数、描述太阳及行星际空间状态的太阳黑子数、太阳射电流量、ACE卫星探测的太阳风速度、太阳风离子密度、行星际磁场南向分量等变量作为输入.

在构建模型输入向量时，将所有变化序列最小时间尺度均化归到10min，并统一为世界时.将地方时、世界时、太阴时、太阳自转周、地球公转周都向圆周投影，以解决类似于“当日的23时”实际上与“次日的0时”非常接近的问题.将当前以及之前的两个变化地磁场实测值（共三个实测值）作为输入，在此基础上依次增加待预测点的各个时间坐标值，包括地方时、世界时、太阴时、太阳自转周时刻、地球公转周时刻以及日期数值等.接着再依次增加当前时刻的Kp指数、Dst指数、太阳黑子数、太阳射电流量.由于ACE卫星处在日地连线的拉格朗日点附近，其观测到的太阳风及行星际磁场参数传递到地球附近，能量输入及地球空间系统的响应有一定时延，借鉴前人研究工作结果[15］，选取当前时刻之前2～3h的太阳风速度、太阳风离子密度、行星际磁场南向分量等数据依次输入模型中（实际上，反映太阳活动性的太阳黑子数和太阳射电流量经过地球空间系统的响应过程，也是有一定时延的.在实验研究过程中，对此也作了考虑，并取得了有意义的结果）.对所有这些因素，均是依次输入，以建模结果来确定最有效的输入因素组合，从而最终确定模型的输入量.输出则为未来第1个时刻的磁场值.经过上述步骤，得到一个单步预测模型.在单步预测模型的基础上，用模型给出的单步预测值更新输入向量，依次类推进行迭代，从而实现多步迭代预测.

3 预测结果与讨论

考虑到变化地磁场活动性不同时，对应的物理过程也不同，从而关键的影响制约因素也会不同.所以，将2009年的数据，按Kp指数的大小分为平静期、中等活动期、较强活动期，分别进行建模预测.同时，按预测期（即预测时间长度）从10min（1步预测）到24h（多步迭代预测），给出模型预测精度的变化曲线.为了比对，采用了两种常见的简单处理方法（以下简称为简单方法），以检验预测模型的有效性.第一种方法是：直接用上一时刻的观测值作为下一时刻的预测值，即如果不考虑磁场变化，经过一定时间后，观察误差会有多大；第二种方法是：直接用上一时刻的观测值加前1个星期的平均日变化在该时段内的变化量作为预测值.用这两种简单方法与本文方法作对比.此外，在辅助导航中，我们关心的是由于变化场的影响，使实测磁场与地磁基准图产生了多大的偏离.因此，统一用平均绝对误差（MAE）作为预测性能指标，以衡量模型的预测精度.

3.1 平静期建模与预测

以2009年第23、24周的数据为例，作平静期建模与预测.图1为该时段的变化地磁场曲线及相应的Kp指数，此时段Kp小于2.5，地磁活动性很低，磁场变化也很有规律.

该模型的输入因素为变化地磁场历史观测数据和地方时.这一方面反映了变化地磁场的地方时依赖性，另一方面也反映出，地磁变化平静时受太阳等空间观测量的影响不大，仅用地磁历史观测数据结合地方时就能实现有效的短期预测.

图2给出了预测期为3h的模型预测结果.图3为不同预测期误差变化曲线，从中可看出，随着预测期的延长，预测误差也在逐步扩大.同时，本文的建模预测方法要明显优于上述简单方法.表1给出了不同预测期下的平均绝对误差.从中可看出，预测期为3h，预测误差为1.40nT.

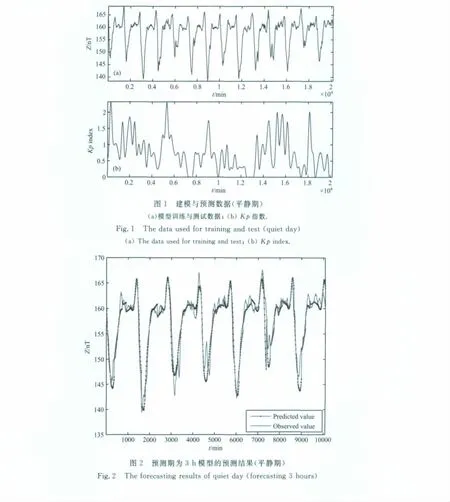
图3 不同预测期误差变化曲线（平静期）Fig.3 Mean absolute error from different forecasting time（quiet day）

表1 不同预测期下的平均绝对误差（平静期）Table 1 Mean absolute error from different forecasting time（quiet day）

3.2 中等活动期建模与预测

以2009年第15、16周的数据为例，做中等活动期建模与预测.图4为该时段的变化地磁场曲线及相应的Kp指数，此时段Kp在3至4之间，地磁活动性较低，磁场变化也较有规律.

该模型的输入因素为变化地磁场历史观测数据、地方时和太阳射电流量（经验证，当太阳射电流量用待预测点时刻之前40min的值作模型输入时，建模精度最高，这反映了地球空间系统响应的延迟，太阳辐射引起大气电离，进而影响电离层电流，从而导致磁场变化）.模型的输入因素反映了变化地磁场的地方时依赖性以及与太阳活动的相关性.

图5给出了预测期为3h，模型的预测结果.图6为不同预测期误差变化曲线，从中可看出，随着预测期的延长，预测误差也在逐步扩大.同时，本文的预测方法在多数预测期上都要优于简单方法.表2给出了不同预测期下的平均绝对误差.从中可看出，预测期为3h，预测误差为1.61nT.

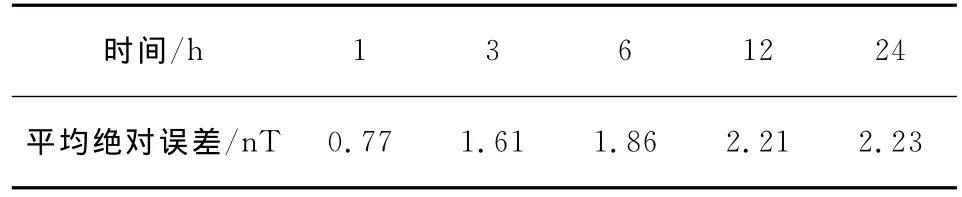
表2 不同预测期下的平均绝对误差（中等活动期）Table 2 Mean absolute error from different forecasting time（middle activity day）

3.3 较高活动期建模与预测

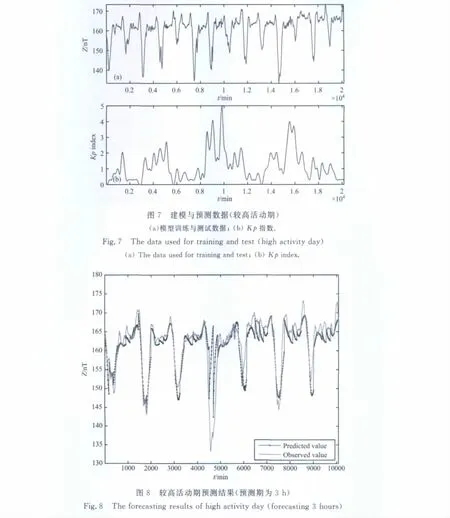
以2009年第25、26周的数据为例，做较高活动期建模与预测.图7为该时段的变化地磁场曲线及相应的Kp指数，此时段最大Kp指数为5，地磁活动性较高，磁场变化也较复杂多样.

图4 建模与预测数据（中等活动期）（a）模型训练与测试数据；（b）Kp指数.Fig.4 The data used for training and test（middle activity day）（a）The data used for training and test；（b）Kpindex.

图5 预测期为3h模型的预测结果（中等活动期）Fig.5 The forecasting results of middle activity day（forecasting 3hours）

图6 不同预测期误差变化曲线（中等活动期）Fig.6 Mean absolute error from different forecasting time（middle activity day）

该模型的输入因素为变化地磁场历史观测数据、地方时和行星际磁场南向分量.模型的输入因素反映了变化地磁场在较高活动水平时和行星际观测量有密切关系.

图8给出了预测期为3h的模型预测结果.图9为不同预测期误差变化曲线，从中可看出，随着预测期的延长，预测误差同样也在逐步扩大.同时，本文的预测方法与直接采用过去7天平均日变化方法效果接近.可见，当地磁活动性增加时，磁场变得复杂多变，预测难度增大，直接采用过去数天的平均日变化方法也许就是简单有效的方法.表3给出了不同预测期下的平均绝对误差.从中可知，预测期为3h，预测误差为2.67nT，明显高于平静期与中等活动期.

表3 不同预测期下的平均绝对误差（较高活动期）Table 3 Mean absolute error from different forecasting time（high activity day）

4 结 论

本文以日地系统观点，综合空间和地面观测数据，采用支持向量机构建了变化地磁场模型，并作预测，有效地提高了低地磁活动期的变化场预测精度.通过本文的工作，主要有以下结论：

（1）随着预测期的延长，预测误差会显著增大，但在较短的预测期内，还是能保持较高的预测精度.

（2）在不同地磁活动程度下，对磁场变化起关键性影响的因素各有不同，因而模型的输入因素会有不同，这是由于变化地磁场在不同活动程度下对应不同物理过程所决定的.

（3）随着地磁活动性的增大，变化地磁场时间演化复杂性增大，预测难度增加.当活动性较强时，直接采用过去数天的平均日变化来预测也许是既简单又有效的方法.不过，随着空间观测和理论研究的进步，本文方法将具有好的前景.

总之，变化地磁场不是孤立的，它是地球空间系统对太阳活动复杂响应过程的结果.将日地系统视作一个整体，根据系统各部分之间的能量、动量、质量的耦合关系，采用现代智能信号处理方法，将空间探测和地面观测有机地结合起来，建立过程的定量关系，构建日地空间统一模型，实现对变化地磁场的综合建模与预测，是提高预测精度的自然之路.实际上，所谓简单方法，可以近似认为是本文方法的一种特例而已.但综合建模的方法涉及因素众多，如何合理地取舍，并把握系统响应对因素变化的延时和累积效应，将是值得深入研究的问题.未来对变化地磁场（其他地球物理场也类似）的精确建模将有赖于观测、理论和计算技术等的发展和有机结合.随着“数字地球”计划等的逐步推进，地球系统的精确建模与预测将有望取得显著进展.值得说明的是，本文模型的时间分辨率为10min，在此基础上，利用谐波拟合或其他插值算法，可以得到任意时间点的变化地磁场值，满足地磁辅助导航要求.

图9 不同预测期误差变化曲线（较高活动期）Fig.9 Mean absolute error from different forecasting time（high activity day）

（References）

[1]徐文耀.地球电磁现象物理学.合肥：中国科学技术大学出版社，2009.Xu W Y.Physics of Electromagnetic Phenomena of the Earth（in Chinese）.Hefei：University of Science and Technology of China Press，2009.

[2]彭纯一，陈兴东.地磁方法在地震短临预报中的应用研究.东北地震研究，2007，23（3）：28-37.Peng C Y，Chen X D.Applicational study on the geomagnetic method for the short-term and imminent earthquake prediction.Seismological Research of Northeast China（in Chinese），2007，23（3）：28-37.

[3]彭富清.地磁模型与地磁导航.海洋测绘，2006，26（2）：73-75.Peng F Q.Geomagnetic model and geomagnetic Navigation.Hydrographic Surveying and Charting （in Chinese），2006，26（2）：73-75.

[4]徐文耀.地磁场的三维巡测和综合建模.地球物理学进展，2007，22（4）：1035-1039.Xu W Y.Three-dimensional survey and comprehensive modeling of geomagnetic field.Progress in Geophysics（in Chinese），2007，22（4）：1035-1039.

[5]徐文耀，区加明，杜爱民.地磁场全球建模和局域建模.地球物理学进展，2011，26（2）：398-415.Xu W Y，Ou J M，Du A M.Geomagnetic field modelling for the globe and a limited region.Progress in Geophysics（in Chinese），2011，26（2）：398-415.

[6]管志宁.地磁场与磁力勘探.北京：地质出版社，2005.Guan Z N.Geomagnetic Field and Magnetic Exploration（in Chinese）.Beijing：Geological Publishing House，2005.

[7]王赤，陈金波，王水.地球变化磁场的分形和混沌特征.地球物理学报，1995，38（1）：16-24.Wang C，Chen J B，Wang S.Fractal and chaotic features for varying component of the earth′s magnetic field.Chinese J.Geophys.（Acta Geophysica Sinica）（in Chinese），1995，38（1）：16-24.

[8]Hongre L，Saihac P，Alexandrescu M，et al.Nonlinear and multifractal approaches of the geomagnetic field.Physics of the Earth and Planetary Interiors，1999，110（3-4）：157-190.

[9]牛超，李夕海，刘代志.地球变化磁场Z分量的混沌动力学特性分析.物理学报，2010，59（5）：3077-3087.Niu C，Li X H，Liu D Z.Chaotic dynamic characteristic of Z component in geomagnetic variation field.Acta Physica Sinica （in Chinese），2010，59（5）：3077-3087.

[10]Sutcliffe P R.The development of a regional geomagnetic daily variation model using neural networks.Ann.Geophysicae，2000，18（1）：120-128.

[11]齐玮.辅助导航地磁变化场实时标识与建模研究[博士论文］.西安：第二炮兵工程大学，2009.Qi W.On Variational Geomagnetic Field Real Time Identifying and Modeling for Assistant Navigation.[Doctor′s thesis］（in Chinese）.Xi′an：The Second Artillery Engineering University，2009.

[12]牛超，李夕海，刘代志.基于混沌理论和LS-SVM的地球变化磁场短时预测.∥ 国家安全地球物理丛书（五）.西安：西安地图出版社，2009：224-229.Niu C，Li X H，Liu D Z.Prediction of the geomagnetic variation field based on chaos theory and LS-SVM.∥National Secure Geophysics Series （5th）（in Chinese）.Xi′an：Xi′an Cartographic Publishing House.2009：224-229.

[13]Yi S H，Huang S Q，Li X H，et al.Modeling and Forecasting of the Variable Geomagnetic Field at Multiple Time Scales.The 10th IEEE International Conference on Signal Processing.Vol.2.Beijing，China，2010：1335-1338.

[14]赵海娟，王家龙，宗位国等.用径向基函数神经网络方法预报太阳黑子数平滑月均值.地球物理学报，2008，51（1）：31-35.Zhao H J，Wang J L，Zong W G，et al.Prediction of the smoothed monthly mean sunspot numbers by means of radial basis function neural networks.Chinese J.Geophys.（in Chinese），2008，50（1）：31-35.

[15]薛炳森，龚建村.利用行星际监测数据进行地磁暴预报.空间科学学报，2006，26（3）：183-186.Xue B S，Gong J C.Forecasting Dst index with artificial neural network.Chinese Journal fo Space Science（in Chinese），2006，26（3）：183-186.

[16]Du A M，Nakamura R，Zhang T L，et al.Fast tailward flows in the plasma sheet boundary layer during a substorm on 9March 2008：THEMIS Observations.J.Geophy.Res.，2011，116：A03216，doi：10.1029／2010JA015969.

[17]Du A M，Sun W，Tsurutani B T，et al.Observations of dawn-dusk aligned polar cap aurora during the substorms of January 21，2005.Planetary and Space Science，2011，59（13）：1551-1558.

[18]Du A M，Xu W Y，Sun W.Experimental evidence of direct penetration of upstream ULF waves from the solar wind into the magnetosphere during the strong magnetic storm of November 9，2004.Planetary and Space Science，2010，58（7-8）：1040-1044.

[19]Du A M，Tsurutani B T，Sun W，et al.Anomalous geomagnetic storm of 21-22January 2005：A storm main phase during northward IMFs.J.Geophy.Res.，2008，113：A10214，doi：10.1029／2008JA013284.

[20]王秋军，杜爱民，赵旭东等.1998年8月6日亚暴期间极光电集流指数AE的特征分析.地球物理学报，2009，52（12）：2943-2950.Wang Q J，Du A M，Zhao X D，et al.Manifestation of the AE index in substorms on August 6，1998.Chinese J.Geophys.（in Chinese），2009，52（12）：2943-2950.

[21]王革丽，杨培才，毛宇清.基于支持向量机方法对非平稳时间序列的预测.物理学报，2008，57（2）：714-719.Wang G L，Yang P C，Mao Y Q.On the application of nonstationary time series prediction based on the SVM method.Acta Physica Sinica （in Chinese），2008，57（2）：714-719.

[22]毛宇清，王咏青，王革丽.支持向量机方法应用于理想时间序列的预测研究.气候与环境研究，2007，12（5）：676-682.Mao Y Q，Wang Y Q，Wang G L.An application study on prediction and analysis for ideal time series based on the SVM method.Climatic and Environmental Research （in Chinese），2007，12（5）：676-682.

[23]叶美盈，汪晓东，张浩然.基于在线最小二乘支持向量机回归的混沌时间序列预测.物理学报，2005，54（6）：2658-2573.Ye M Y，Wang X D，Zhang H R.Chaotic time series forecasting using online least squares support vector machine regression.Acta Physica Sinica （in Chinese），2005，54（6）：2658-2573.

[24]Suykens J A K，Gestel T V，Brahanter J D，et al.Least squares support vector machines.Singapore：World Scientific，2002.

[25]乔玉坤，王仕成，张琪.地磁匹配特征量的选择.地震地磁观测与研究，2007，28（1）：42-47.Qiao Y K，Wang S C，Zhang Q.Selection of the characteristic variable of geomagnetic for matching.Seismological and Geomagnetic Observation and Research，2007，28（1）：42-47.

[26]齐玮，王秀芳，李夕海等.基于统计建模的地磁匹配特征量选择.地球物理学进展，2010，25（1）：324-330.Qi W，Wang X F，Li X H，et al.Selection of characteristic components for geomagnetic matching based on statistical modeling.Progress in Geophysics （in Chinese），2010，25（1）：324-330.

[27]Cen G X，Xu W Y，Du A M.Statistical characteristics of the day-to-day variability in the geomagnetic Sq field.J.Geophys.Res.，2007，112：A06320，doi：10.1029／2006JA012059.