交流矢量调速系统继电反馈PID整定法

康现伟，李 鹏，王胜勇，卢家斌，王国强

（中冶南方（武汉）自动化有限公司，湖北武汉430205）

1 引言

按照偏差的比例（Proportional）、积分（Integral）和微分（Derivative）进行控制的调节器简称PID调节器。由于其算法简便、鲁棒性好、可靠性高等优点，PID控制算法被广泛应用于工业过程控制。

当前工业控制的状况表明90%以上的控制回路是采用PID控制策略［1]，在石化、化工、造纸等工业领域，甚至有97%的常规控制器都是PID控制器。因此，PID控制器可以视为自动控制的“面包与黄油”。

PID控制器在实际应用时需要进行参数整定。早期的参数都采用手动整定，现场工程师通过一系列调节试验绘制出过程动态特性曲线或频率响应曲线，再通过这些曲线由整定公式计算出PID参数。整个整定过程既费时又费力。而且实际生产往往具有非线性、不确定性，难以建立精确的数学模型，常规的PID控制器难以达到理想的控制效果。由于参数整定方法烦杂，常规PID控制器参数往往整定不良、性能欠佳，难以适应复杂环境。针对以上问题，人们一直在研究PID控制器参数的自整定技术，以适应复杂的工况和高性能指标的控制要求。随着现代电子技术和计算机技术的飞速发展，PID控制器的自整定技术也在近二十年来取得了长足的进步。自整定的发展减少了控制工程师现场调试工作量，节省了大量时间，且整定结果更加可靠，使一些复杂但是更加精细的设计方法能够应用于实际过程工业控制［2，3]。

本文首先介绍一些常用的整定公式，这些整定公式可以直接应用于PID自整定控制器。详细分析了继电反馈自整定方法，并推导出适用于工程的整定公式，将其应用到了交流矢量调速系统的PI参数自整定中。

2 PID参数自整定

在长期的工程实践中，人们已经积累了大量使用PID控制策略的经验。尤其是在工业过程控制中，由于控制对象的精确数学模型难以建立，系统参数又经常发生变化，因而运用现代控制理论进行分析、综合会耗费很大代价进行模型辩识，且往往不能得到预期的效果，所以人们常用PID调节器，并根据经验进行参数整定。几十年来，PID控制的参数整定方法和技术处于不断发展中，特别是近年来，国际自动控制领域对PID控制参数整定方法的研究仍在继续，许多重要国际杂志不断发表新的研究成果，PID控制的参数整定方法和技术也处于不断发展中。

2.1 Z-N参数整定方法

齐格勒-尼柯尔斯（Ziegler-Nichols）在大量实验的基础上，于1942年提出了一种实用的参数整定规则，简称 Z-N 规则［4～6]。

Z-N法中最常用的是响应曲线法，即在被控对象的输入端加一个阶跃信号，然后测出输出的阶跃响应曲线。如果被控对象既无积分环节，又无共轭复数极点存在，则阶跃响应曲线呈S型，如图1所示。

该曲线的特性可以用测得的延迟时间τ和时间常数T来表征，其相应的数学模型可以式（1）的传递函数近似地描述：

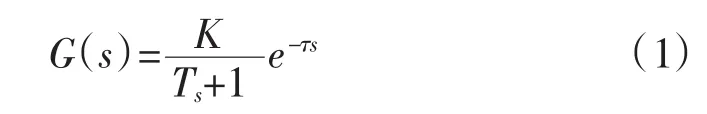
根据实验测得参数τ、T，再按照表1的规则。即可整定PID控制器的参数。

2.2 继电反馈法

Asortm和Hagglund在1984年提出基于继电反馈控制的PID参数整定法。

图1 阶跃响应曲线

表1 响应曲线法整定PID参数

继电反馈法是在闭环控制回路中加入继电控制，继电可以是带滞后的也可以不带滞后，利用继电控制的非线性特性使被控过程出现极限环振荡，这个振荡是周期性的，通过测量这个极限环的性质，获得过程的临界动态特性参数，即输出的频率与振幅，就可以测知对象临界点的信息，再利用ZN临界比例度整定公式获得PID控制器参数［7，8]。

继电反馈自整定技术有许多突出的优点。首先，这种方法耗时较少且易于使用，操作者只需简单地按下一个按键，即可自动整定出PID控制器参数；其次，继电反馈自整定调节试验是闭环进行的，适当选择继电参数可以使过程的频率响应维持在设定点附近，整个过程会处于线性区域，因此继电反馈自整定方法有可能适用于高度非线性的过程；第三，这种方法不需要先验知识来选取采样率，对于一些复杂的自适应控制器尤其有效。该方法简单、可靠、易于使用，已经广泛应用于工业PID控制器的参数自动整定。

3 适用于交流矢量调速系统的继电反馈PID整定法

在实际应用中，原始Z-N法的阶跃响应曲线法以及临界振荡法容易造成过流或电机失控而导致故障，难以应用到由交流矢量调速系统中，本文将继电反馈法应用于交流矢量调速系统。

在交流矢量调速系统中，通常都只采用PI控制器，其参数可以通过构建控制系统的传递函数模型来计算，但这种方法过于理想化，在构建出的模型里许多参数都采用了近似计算，公式复杂、变量过多导致精度降低，而且在实际的系统中，由于周围环境和设备自身的物理特性的影响，由控制模型计算出的PI参数往往不能满足工程应用的需求。继电反馈法原理简单，采用的变量较少且易于采集，因此本文将其应用于交流矢量调速系统，整个控制系统如图2所示。

图2 采用继电反馈法的交流矢量调速系统

该系统由转矩环、磁通环和速度环组成，转矩环、磁通环实际上是同级的内环（电流环），而速度环则是外环，内外环组成了双闭环调速系统。对于双闭环系统，输出的速度对内环的PI参数不敏感，因此该系统电流环采用传递函数计算出PI参数；外环速度环的PI参数直接影响系统的输出，因此采用继电反馈法整定PI参数。

在实际的工业过程控制中，继电控制信号往往是系统执行器的输入信号，该信号不能为负值。继电振荡的PID参数自整定算法的控制过程曲线如图3所示。被控对象只要在高频具有至少-π的相位之后就可在继电反馈状态下产生周期为T的等幅振荡，而其频率正是使被控对象相位滞后-π的频率，即奈氏曲线与负实轴焦点的频率ωn。设继电特性幅值为d，被控对象的输出为y（设被控对象振幅为a），由傅里叶级数展开继电特性输出可知，在临界频率ωn处的幅值近似为：

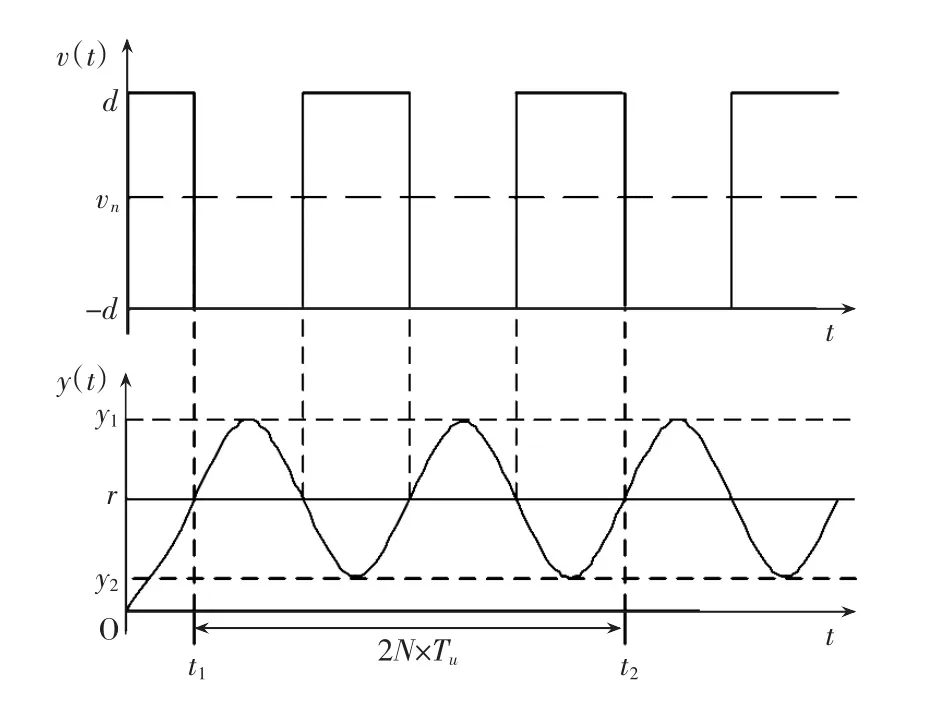
图3 自整定过程曲线

在实际测量时，为了消除环境以及被控对象物理特性的干扰，得到稳定的振荡波形，从第二个周期开始采样，截取N个完整的振荡周期，由图3可求出振幅A与振荡周期Tu，测量公式为：

其中：A为系统输出的振幅，Tu为临界振荡周期，y1为实际输出速度的波峰值，y2为波谷值，t1和t2分别是采样开始时间和结束时间。在测得A和Tu后，根据原始Z-N法中的临界振荡法，可以推得：

由式（2）～（6）可以推导出：

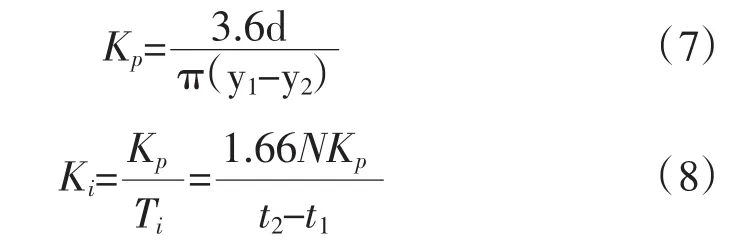
其中：d是实际输入目标值，即为给定的速度阶跃信号振幅。

4 PI参数整定实验及结果

实验采用的平台为变频器（CPU为TI的F2812 DSP）控制的对拖机组（7.5kW交流异步电机和作为负载的同轴直流电机），程序运行于DSP中。

进行两个实验，首先采用闭环继电振荡法整定PI参数，再采用原始Z－N法（临界振荡）计算出另一组PI参数。然后分别采用这两组PI参数对电机进行阶跃响应实验和稳速运行实验，记录相应的实验参数并加以比较。

4.1 PI整定实验

闭环继电反馈整定程序流程。

（1）通常继电振荡实验需在0频附近振荡，即振荡中线频率为0Hz，但为了测量，此处设定图3中振荡中线频率vn为15Hz。由于是采用的是闭环继电振荡，因此实际振幅比设定值通常要小很多，为了便于采样及提高计算精度，采用了较大的振幅给定值15。

（2）先给交流电机通励磁电流，等待一个直流磁化时间（即磁场建立所需要的时间，约等于转子时间常数），给电机输入一个30Hz的速度阶跃给定值。

（3）当电机速度达到vn时，立即将输入给定值设为0Hz的阶跃信号，此时由于惯性电机的转度仍会继续升高，到达峰值y1后就会减速。

（4）当电机速度下降为vn时，立即将输入给定值重新设为30Hz的阶跃信号，此时电机速度会先减小至y2，然后会开始加速。

（5）重复步骤3、4直到产生稳定的速度振荡（即多次y1的测量值都相同）并开始采样，当采集到N个完整振荡周期后停机。

（6）根据式（7）、（8）计算出速度环 PI参数。

图4所示为连续整定过程，需要注意的是，本文所介绍的方法是在闭环状态下进行的，需对电机安装编码器。

采用原始Z－N法（临界振荡）整定出的PI参数的方法较为常见，大多数教科书上都有介绍，因此这里不再赘述。

图4 变频器闭环继电反馈自整定过程曲线

4.2 性能比较实验

对两种方法整定出的参数分别施加10Hz的速度阶跃信号，其实验结果如图5所示。对于稳速运行状态，两种方法的速度脉动曲线如图6所示，其中纵坐标为额定频率的百分比，20%为10Hz。两种方法整定出的参数对比如表2所示。

图5 速度阶跃响应曲线

图6 速度脉动（纵坐标为额定频率50Hz的百分比）

表2 两次自整定结果

由实验结果可知，继电反馈法可以良好地应用于实际的交流矢量调速系统中，其整定效果远好于原始Z－N法，其主要优点有：

（1）整定时间短。由图4可以看到，整个闭环继电反馈整定过程不超过1s，极大地提高了PI参数的设置效率。

（2）整定后动态性能好。由图5和表2可知，与传统的Z－N法相比，通过继电反馈整定的PI参数上升和稳定时间短、超调量小，具体参数见表2。

（3）稳速运行时脉动小且波形稳定。由图6可以看到，继电反馈法整定出的PI参数在稳速运行时脉动很小，其速度波形规则、稳定，而Z－N法的速度波形则显得较为杂乱且有小幅波动。

5 结论

本文介绍了PID参数自整定的几种方法，并将继电反馈法按工程应用的需求加以简化，为了保护电机，将该方法改进为闭环下使用，减小了电机在整定时转速的实际振幅，将该方法应用于实际的交流矢量调速系统中。实验结果表明，采用继电振荡法取得了良好的整定效果，大大提高了变频器调节PI参数的效率及准确性，解决了实际工程中PI参数的整定基本靠手动调节的问题。

［1] Astrom.K.J，Hagglund，T.PID Controllers：Theory，Design and Tuning.Instrument Society of America，1995.

［2] 曹承志.微型计算机控制新技术［M] .北京：机械工业出版社，2001.150－165.

［3] 陶永华.PID控制原理和自整定策略［J] .工业仪表和自动化装置，1997，（4）：60－64.

［4] 王 伟，张晶涛，柴天佑.PID参数先进整定方法综述［J] .自动化学报，2000.26：347－355.

［5] 张晋格.控制系统CAD－基于MATLAB语言［M] .机械工业出版社，2004，162－164.

［6] 钱积新，王 慧，周立芳.控制系统的数字仿真及计算机辅助设计［M] .北京：化学工业出版社，2003.132－136.

［7] 谢元旦，夏淑艳.PID调节器参数的继电自整定方法［J] .控制与决策，1993，8（1）：77－79.

［8] 杨 智.自整定PID调节器设计方法［J] .甘肃工业大学学报，1998，24（1）：79－81.