低渗透油藏七点井网的有效动用程度

王军磊，周明旺，罗二辉，韩海水

（1.中国石油勘探开发研究院，北京100083； 2.辽河油田分公司 勘探开发研究院，辽宁 盘锦 124010）

0 引言

随着油气供给形势日趋紧张，人们投入到非常规油气藏（低渗透—超低渗透油藏、页岩气、煤层气等）的研究中.低渗透油藏的孔喉细小、结构复杂、渗流阻力大，流动时存在启动压力梯度现象，Song F Q等［1］通过实验发现启动压力梯度存在于微孔道中，且与孔道半径呈现半对数直线关系；Song F Q等［2］利用不同的边界层润湿性测试启动压力梯度，指出改变边界层润湿性能减小流体流动阻力；姚约东 、邓英尔、熊伟等［3-5］采用不同数学模型描述非线性流动现象.另外，启动压力梯度产生动边界问题［6-7］，王晓冬等［8］指出动边界传播受油井产量控制，油井产量越大，动边界传播越快；李爱芬等［9］通过渐进分析方法研究定压生产时油井的动边界运动规律，提出把油井见效时间做为合理井距的判断依据；Song H Q等［10］指出，启动压力梯度越大，含水致密气藏的压力传播距离越短.

计秉玉等［11］指出，在存在启动压力梯度的情况下，井网中只有部分原油得到动用，假设流体流动的轨迹是一条折线（实际是曲线），用三角流管计算不同井网下的有效动用因数；朱维耀等［12］在单井中提出一个控制半径的概念，应用到五点井网中近似计算井网有效动用因数.不论是三角流管法还是控制半径法都是针对实际流体流动线性数学模型.笔者采用流线模拟方法直观展示流体流动区和不动区，利用流线积分法计算井网有效动用因数，并结合实例做相关参数的敏感度分析.

1 渗流模型

在无限大均质储层中，n口油、水井（视为源汇项）同时生产，不考虑流体、岩石的压缩性及油水的流度差异，保持注采平衡，其质量守恒定理和渗流规律（流体在低渗透油藏中的流动是非线性的）分别表述为

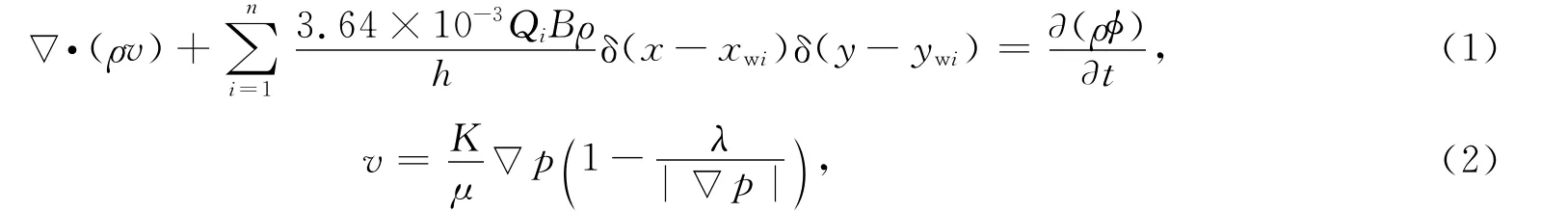
式（1-2）中：K为地层渗透率；ρ为原油密度；B为原油体积系数；h为储层厚度；φ为储层孔隙度；t为时间；p为储层压力；λ为启动压力梯度；d为油水井距；v为渗流速度；Qi、xwi、ywi分别为第i口井产量及坐标；δ为狄利克函数.

将式（2）代入式（1）可得二维直角坐标系下的井网压力控制方程为

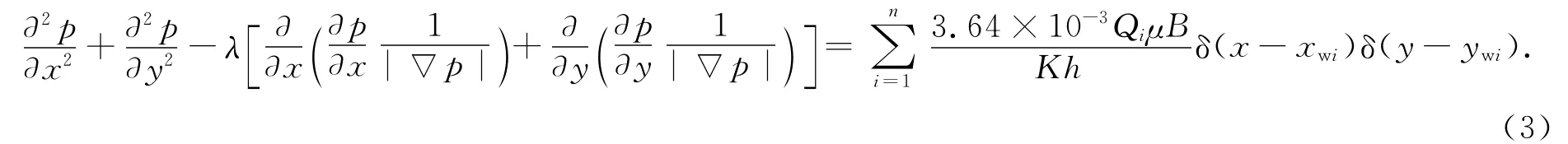
式（3）为非齐次线性方程，根据叠加原理将方程（3）分解为

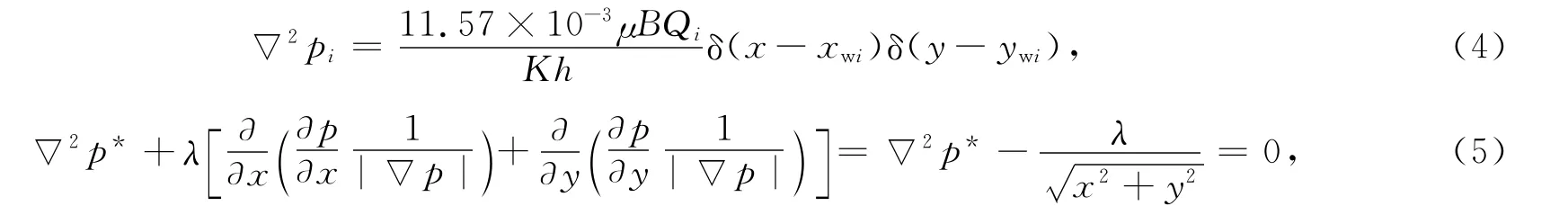
低渗透油藏井网的压力公式为

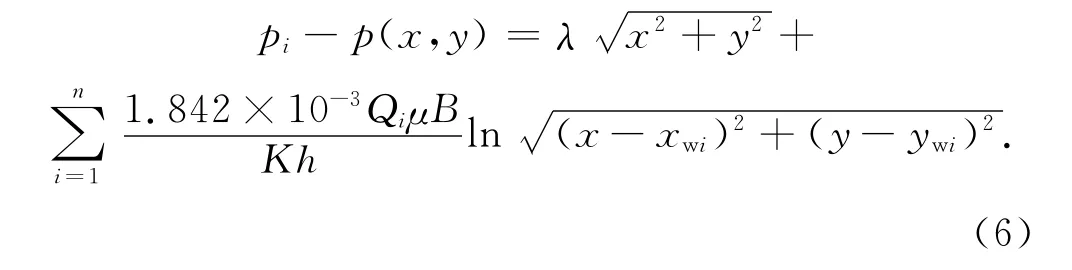
对于七点井网，注采关系见图1.选择一口注水井作为原点，绿色实线所包围的区域为一个井网单元.

利用注采平衡关系式Q1＝2Q2，结合贝塞尔公式［13］对式（6）进行处理，得低渗透七点井网的量纲一的压力公式为

在式（7）的基础上求解渗流速度场，从而获得整个流线场，以识别井网单元内的流动区及不动区，进而计算井网对原油的有效动用程度.

2 井网流线及有效动用因数

流线能直观描述流体运动的实际轨迹，流体质点沿流线从注水井出发至生产井结束，Pollock D W［14］提出的质点追踪法和Lebanc J L等［15］的解析流函数法能模拟流线.对于解析流线解，由于速度场来源于压力场，故可对速度场vxD沿yD积分而直接得到流函数.低渗透七点井网流函数表达式为

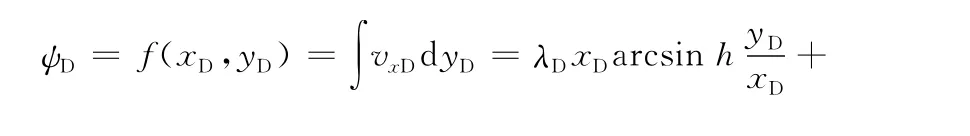
式中：ψD为常数，对应一条流线.流线方程满足f（xD，yD）-ψD＝0，其中在注水井点（xD→0，yD→0）式（8）可以近似表示为

此时流线方程可以写成yD≈xDtanψD，同理在生产井附近流线满足yD≈（1-xD）tanψD，表明流函数ψD是流线与主流线的夹角（水淹角），如果直接从水淹角引出直线，就构成常用的三角流管［11］.在1／12井网单元中水淹角ψD的变化范围为0～π／3，给定ψD后式（8）形成xD与yD之间的超越方程.利用数值方法可以快速计算相应的流线，在给定一系列的ψD后即可获得整个井网单元的流线分布.

在实际工程中，流体质点沿不同流线自注水井向采油井流动，并逐渐远离主流线，驱动压力梯度不断下降.当运动至驱动压力梯度小于启动压力梯度的空间点时，流体质点将不能按照原有的路径继续运动，而将朝主流线方向收缩以获得更大的驱动压力梯度，导致井间部分区域无法得到有效驱替而形成非流动区.计算不同量纲一的启动压力梯度下七点井网单元流线分布，见图2，其中蓝线所覆盖的区域为流动区.

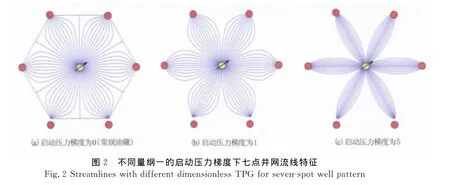
由图2可知，当量纲一的启动压力梯度为0时，即不存在启动压力梯度，流体质点流动到各处的驱动压力梯度不小于0，整个井网单元中分布流线，所有区域内的原油能够得到有效动用；当存在启动压力梯度时，流体质点沿流线开始朝主流线方向收缩，启动压力梯度越大，收缩程度越剧烈，意味着有效动用的区域不断减小，开发效果变差.在相同的注采条件下，启动压力梯度越大，剩余油富集区越大.

主流线（ψD＝0）与最外侧流线（ψD＝π／3）所包围的区域为井网有效动用的区域（流动区），通过对最外侧流线进行面积积分即可得到有效动用区域.定义有效动用因数为流动区面积与井网单元面积的比，其中流动区面积为

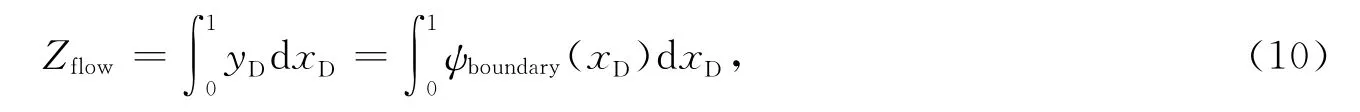
此处yD＝ψboundary（xD）为最外侧流线，满足公式

利用式（10）计算不同量纲一的启动压力梯度λD下的井网有效动用因数，见图3.当λD＝0时，有效动用因数为1，说明对于常规油藏，只要驱替时间足够长井网单元中的流体都能被有效动用（见图2（a））.当量纲一的启动压力梯度增大时，有效动用因数降低，变化趋势随量纲一的启动压力梯度增大逐渐变缓.

3 井网有效动用程度敏感度分析

由式（11）和图3可知，量纲一的启动压力梯度与有效动用因数呈单调反相关关系，结合量纲一的启动压力梯度定义，可得有效动用因数（SDC）与各个影响因素的相关性通式为

根据式（12），通过3个途径提高井网对原油的有效动用程度：

（1）增加地层有效渗透率.启动压力梯度与岩心渗透率往往呈现指数关系，如λ＝aK-n［16］（a、n为实验参数，通过数据拟合获得）.酸化或压裂是增大地层有效渗透率的常用手段.

（2）缩短井距.对低渗透油藏，缩小注采井距且在剩余油富集区部署加密井，将大大减小量纲一的启动压力梯度，提高有效动用因数.这种方法在低渗透油藏中后期调整中广泛使用.

（3）增大注采压差.增大注采压差能提高有效动用因数，但不能无限增大，它受到泡点压力和地层破裂压力的束缚.一般来说，注采压差应该保证采油井底压力高于泡点压力，而注水井底压力低于地层破裂压力.

增大地层有效渗透率、缩短井距和增大注采压差都能提高有效动用因数，但这些变量对不同储层的敏感程度不一.对于某个低渗透油藏（渗透率固定），缩短井距和增大生产压差往往存在最佳选择，以某油田为例，分析这种敏感性.某油田不同区块的岩样测试数据整理见表1.

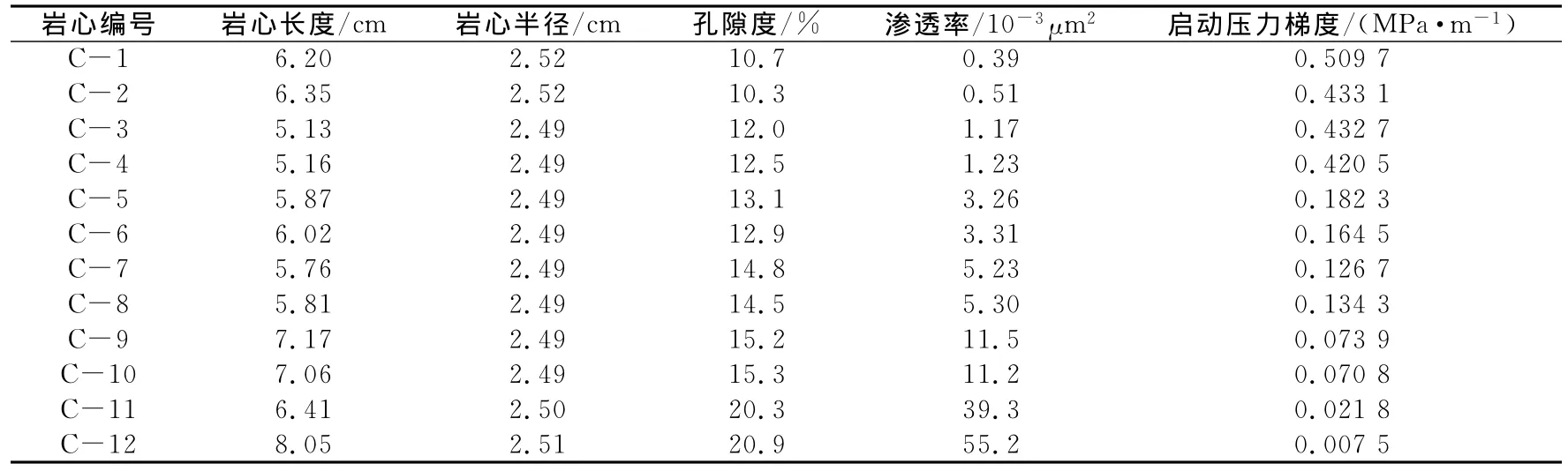
表1 某油田多个岩样测试数据Table.1 Parameters of core analysis and experimental TPGs based on some oilfield

通过线性回归，可以得到启动压力梯度与渗透率的函数表达式

选取8个低渗透区块进行计算，储层平均有效厚度为5m，地层原油黏度为5mPa·s，对应的渗透率分别为（0.67，0.83，1.08，1.26，1.51，1.87，2.42，5.45）×10-3μm2，井距调整范围为100～600m，注采压差在5～20MPa之间调整.

（1）油水井距影响.对不同区块，当注采压差固定时，有效动用因数随井距增大而增大，但变化趋势有所区别.当地层渗透相对较小时（如（0.67，0.835）×10-3μm2），曲线斜率的绝对值较大，表明缩小井距能大大增大井网的有效动用因数（见图4（a））.

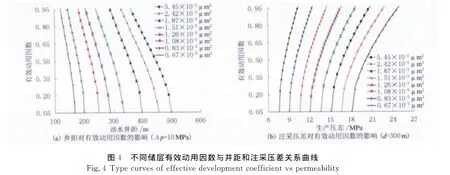
（2）注采压差影响.有效动用因数与注采压差存在正相关.当储层渗透率相对较高时，有效动用因数对注采压差更为敏感，小幅度增大注采压差能大大增加井网有效动用因数（见图4（b））.

4 结论

（1）由于存在启动压力梯度，流体在低渗透油藏中的流动规律异于常规油藏的.只有当注采压差能克服启动压力梯度的影响时，流体才参与流动；否则，将处于静止状态.

（2）对低渗透油藏，流线不能覆盖整个井网区域.不同的油藏，采用同样的井网动用程度不同，它随启动压力梯度的增大而减小.压裂酸化增加地层有效渗透率、提高注采压差、缩短井距都能提高井网的有效动用程度.

（3）储层渗透率越小，缩短井距对井网动用程度的提高更有益；较好的储层条件时，提高注采压差能大大提高井网动用程度.

［1］Song F Q，Bian S L.Measurement of threshold pressure gradient of microchannels by static method［J］.Chinese Physics Letters，2007，24（7）：1995-1998.

［2］Song F Q，Wang J D，Liu H L.Static threshold pressure gradient characteristics of liquid influenced by boundary wettability［J］.Chinese Physics Letters，2010，27（2）：111-120.

［3］姚约东，葛家理.低渗透油层非达西渗流规律的研究［J］.新疆石油地质，2000，21（3）：213-216.Yao Yuedong，Ge Jiali.Study on non-darcy flow pattern in low permeability oil reservoir［J］.Xinjiang Petroleum Geology，2000，21（3）：213-216.

［4］邓英尔，刘慈群.低渗油藏非线性渗流规律数学模型及其应用［J］.石油学报，2001，22（4）：72-78.Deng Yinger，Liu Ciqun.Mathematical model of nonlinear flow law in low permeability porous media and its application［J］.Acta Petrolei Sinica，2001，22（4）：72-78.

［5］熊伟，雷群，刘先贵，等.低渗透油藏拟启动压力梯度［J］.石油勘探与开发，2009，36（2）：232-236.Xiong Wei，Lei Qun，Liu Xiangui，et al.Pseudo threshold pressure gradient to flow for low permeability reservoirs［J］.Petroleum exploration and development，2009，36（2）：232-236.

［6］Pascal F，Pascal H，Murray D W.Consolidation with threshold gradients［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1981，5（3）：247-261.

［7］计秉玉，何应付.基于低速非达西渗流的单井压力分布特征［J］.石油学报，2011，32（3）：466-469.Ji Bingyu，He Yingfu.Formation pressure distribution of a single well based on low velocity non-Darcy flow［J］.Acta Petrolei Sinica，2011，32（3）：466-469.

［8］王晓冬，侯晓春，郝明强，等.低渗透介质有启动压力梯度的不稳态压力分析［J］.石油学报，2011，32（5）：847-851.Wang Xiaodong，Hou Xiaochun，Hao Mingqiang，et al.Pressure transient analysis in low-permeability media with threshold gradients［J］.Acta Petrolei Sinica，2011，32（5）：847-851.

［9］李爱芬，刘艳霞，张化强，等.用逐步稳态替换法确定低渗透油藏合理井距［J］.中国石油大学学报：自然科学版，2011，35（1）：89-93.Li Aifen，Liu Yanxia，Zhang Huaqiang，et al.Determination of reasonable spacing in low permeability reservoirs by means of series of steady state analysis［J］.Journal of University of Petroleum，2011，35（1）：89-93.

［10］Song H Q，Zhu W Y.A study of effective deployment in ultra-low-permeability reservoirs with non-darcy flow ［J］.Petroleum Science and Technology，2010，28（16）：1700-1711.

［11］计秉玉，李莉，王春艳.低渗透油藏非达西渗流面积井网产油量计算方法［J］.石油学报，2008，29（2）：256-261.Ji Bingyu，Li Li，Wang Chunyan.Oil production calculation for areal well pattern of low-permeability reservoir with non-darcy seepage flow［J］.Acta Petrolei Sinica，2008，29（2）：256-261.

［12］朱维耀，刘今子，宋洪庆，等.低／特低渗透油藏非达西渗流有效动用计算方法［J］.石油学报，2010，31（3）：452-457.Zhu Weiyao，Liu Jinzi，Song Hongqing，et al.Calculation of effective startup degree of non-darcy flow in low or ultra-low permeability reservoirs［J］.Acta Petrolei Sinica，2010，31（3）：452-457.

［13］孔祥言.高等渗流力学［M］.合肥：中国科技大学出版社，1999：89-97.Kong Xiangyan.Advanced mechanics of fluid in porous media［M］.Hefei：University of Science ＆ Technology Press，1999：89-97.

［14］Pollock D W.Semianalytical computation of path lines for finite-difference models［J］.Ground Water，1988，26（6）：743-750.

［15］Lebanc J L，Caudle B H.A streamline model for secondary recovery［C］.SPE 2865，1971.

［16］贾振岐，赵辉，汶锋刚.低渗透油藏极限井距的确定［J］.大庆石油学院学报，2006，30（1）：104-107.Jia Zhenqi，Zhao Hui，Wen Fenggang.Oil well production on non-linear flow in low permeability oil reservoir［J］.Journal of Daqing petroleum institute，2006，30（1）：104-107.