基于实物期权模型的土地供应时机分析

李红波，刘亚丽

(昆明理工大学建筑工程学院，云南昆明 650500)

土地供应政策参与国家宏观经济调控发挥了重要作用。国家通过土地供应量的控制和供应结构的管制实现对住房价格的调控［1-2］，完善土地供应方式影响居住用地市场［3］，运用经济、法律和行政等多种手段调控土地供应总量和结构、市场准入、土地价格等，实现宏观调控的目标［4］。部分研究表明［5］，由于受调控主体、城市土地市场运行状况、调控的体制环境及实施机制、政策工具自身特性的综合影响，土地供应政策发挥作用与效果存在时滞。因此，设定一定的指标来反映政策工具的“超前”或“滞后”，提高政府对市场运行态势的预测、判断能力，把握好调控力度及调控时间，根据用地需求变化适时调整供地量，把握好供地节奏和时机，有利于房价的稳定和房地产宏观调控目标的实现。

城市土地需求差异转换、市场竞争加剧、外部经济环境时好时坏、银根时紧时松、利率变化等因素导致土地市场行情的动态性和不确定性，行情的不确定性变化要求地方政府具有一定应变能力，能在变化的行情中把握土地供应策略和时机。土地是房地产经济的直接生产要素，土地供应成为调控过热房地产市场的直接有效工具，要兼顾土地供应产生的经济效益和社会效益。因此，如何分析、应对土地市场行情的不确定性，有必要探讨土地供应时机问题。

一、土地供应的实物期权

在期权理论中，其标的资产可以是实物商品(如土地、房屋、工厂、矿产等)、金融商品(如股票、债券等)，也可是期货。如标的资产是金融商品或金融期权合约，则这样的期权为金融期权;如果是实物商品，则这样的期权为实物期权。两者的本质区别在于标的资产类型不同。两类资产的特性决定了两种期权的区别，也存在一定的关联性。持有土地的价值期权与金融期权之间存在密切联系，如表1。

表1 金融期权与土地实物期权的比较［6］

无论是金融期权还是实物期权都是一种选择权。期权赋予持有者一种作出某种选择的权利，但持有者不用必须行使该权利。实物期权是指存在于实物资产投资中，具有期权性质的权利，广义的理解可以认为是决策者对投资项目的选择权，即是决策者在付出一定成本后便拥有了在一定的时间里投资或不投资、以怎样的方式投资、决定投资规模大小等的权利，也即是决策者拥有投资的灵活性。这种灵活性使决策者能够应对环境的不确定性，是具有价值的。而传统的项目评价方法为折现现金流方法(简称DCF)，通过计算地块出让年限内的净现值(简称NPV)，没有体现这种灵活性的价值，其结果导致项目投资价值低估。NPV应用于土地开发投资进行评估，导致对开发价值的低估，从而使投资者丧失更好的供地时机。实物期权模型应用于土地开发决策在部分文献有所探讨［7-9］，研究结果表明，土地的价值应当由净现值和灵活性价值两部分组成：地块价值 =NPV+灵活性价值。

国外很多文献借用实物期权理论研究土地开发时机选择［10-12］，但未见文献阐述政府土地供应时机问题。一般而言，私有制下的土地供应主体多元化，政府制定土地市场规则并监督执行，而不参与土地市场经营活动。

在中国土地市场，从政府作为土地供应方来看，也可尝试运用期权的观点看待土地供应时机，解释土地市场不确定性问题。笔者拟用实物期权方法，根据土地市场不确定性特征，充分考虑地块的时间价值和管理柔性以及不确定性的信息带来的土地价值。

二、实物期权模型

假定土地储备中心购买土地价格为p0，动态地价p()t服从几何布朗运动：

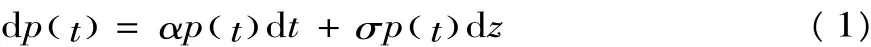
其中，α是地价p的漂移参数，即是p的瞬时增长率，σ是地价p的方差参数即是p期望增长率的标准差，而dz是维纳过程的增量，服从均值为0、方差为dt的正态分布(dz=ε，ε～N(0，1)，E(dz)=0)。

式(1)表明，随着时间推移，政府会得到更多的新信息，但土地未来价值一直不确定，而且对土地储备越久的地块估计价值，其方差越大，即越不准确，体现了观望的灵活性及其价值。

土地供应时机等同于永久性看涨期权，拥有以预先确定的土地价格p()t供应土地的权利而不是义务，土地供应时机选择决定何时执行看涨期权，问题转化为期权定价问题，期权价格p()t由其最佳执行时间和执行时的净收益确定。如果土地期权价值确定，那么最佳执行时间也将被确定，为了寻找最佳土地供应时机，就要找到当前的期权价值。

地方政府土地供应收益风险中性，设无风险利率为r，土地期权价值在时刻t的表达式：

地方政府通过选择最佳土地供应时刻T来实现最大土地期权价值F(p)，注意到持有期权本身不会产生现金流：

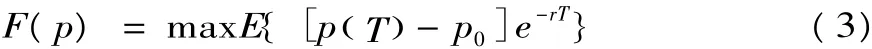
式中：T为土地供应的未来时间，p(T) 为T时刻土地价格，e-rT为按连续复利率r计算的折现因子。

土地供应时机选择需要作出的决策是开始供应或继续等待，决策看作构成了一个连续时间上的最优停止时间。持有期权本身并不能产生现金流。持有它的唯一回报是资本利得，因此可得到在土地供应之前dt时间段的贝尔曼方程(Bell Equation)为：

式(4)的经济意义是，一项土地资产在时间段dt价值的预期变化E( dF) ，应等于该项资产的无风险收益rFdt。利用Ito引理展开dF，得到方程带入贝尔曼方程，整理移项，消去dt，得到与时间无关的Black-Scholes期权定价偏微分方程［13］：

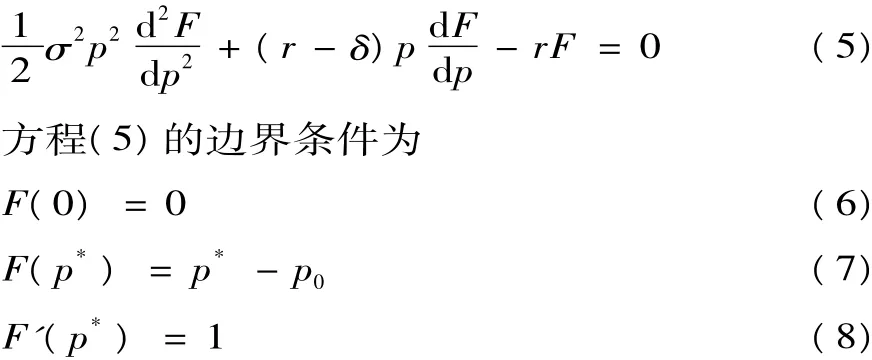
δ=r-a表示r与a之间的差异，经济意义是土地供应的机会损失。式(6)表示当土地供应时无购地者，土地交易未发生，土地供应无效，不产生收益，所以期权价值为F(0)=0。式(7)给出在参照时点，即T=0时，推迟供应或马上供应的临界值p=p*，则有F(p*)=p*-p0。式(8)给出了光滑粘连条件(价值匹配条件)，对临界值p*，有F'(p*)=1。

方程(5)是典型欧拉齐次方程，则实物期权价值的二阶常微分方程式的特征根为：

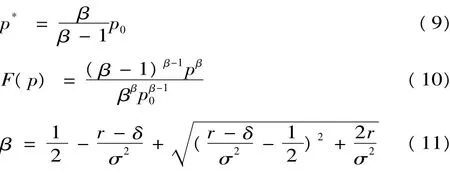
式(9)给出了土地供应的临界条件，即p≥p*。式(10)描述了在土地价格p0条件下，实物期权价值F(p)与土地价格p之间的关系。式(11)是F(p)中参数β的描述。式(9)和(10)给出了土地供应的最优规则及土地价值，即临界值p*。

三、土地供应最优时机特征

在土地供应的最优时点，分析各参数变化幅度对于土地供应最优时机的影响，通过MATLAB软件，分别分析σ、δ、r变化引起期权价值F(p)和临界值p*的变化进行模拟。

其一，当不确定性 σ提高时，δ=0.01，r=0.05，而p0分别取10和30对比模拟，期权价值F(p)增加，临界值p*也提高。土地市场的不确定性增加了土地供应的机会价值，意味着当土地市场变得更加不确定时，土地市场价值可能会上升。从模拟曲线可见，F(p)、p*对σ成近似线性关系，F(p)、p*的绝对变化幅度与初始土地价格p0相关，p0越大，F(p)、p*的变化幅度越大。

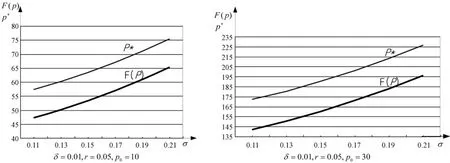
图1 不确定性σ与期权价值F(p)和临界值p*关系模拟曲线

其二，当机会损失 δ提高时，σ =0.15，r=0.05，而p0分别取10和30对比模拟，期权价值F(p)下降，从而临界值p*下降。机会损失δ变得越多，p的预期增长率下降，期权价值F(p)越低。从模拟曲线可见，F(p)、p*对δ曲线斜率逐渐变小，F(p)、p*的变化幅度随δ增大而变小，同时F(p)、p*的绝对变化幅度与初始土地价格p0相关，p0越大，F(p)、p*的变化幅度越大。

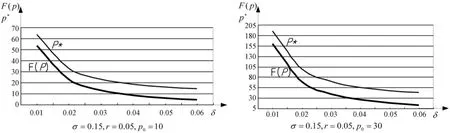
图2 机会损失δ与期权价值F(p)和临界值p*模拟曲线

其三，若无风险利率r提高，δ=0.01，σ =0.15，而p0分别取10和30对比模拟，则期权价值F(p)增加，因而临界值p*也提高。由于未来时刻T的成本价格p0的现值为p0e-rT，若供应土地就获得的回报的现值为p0e-δT。因此，若δ固定，r提高会降低土地购置成本的现值，但不会降低其回报，即收益与成本之差相对固定。从模拟曲线可见，F(p)、p*对r几乎成线性关系，F(p)、p*的绝对变化幅度与初始土地价格p0相关，p0越大，F(p)、p*的变化幅度越大。

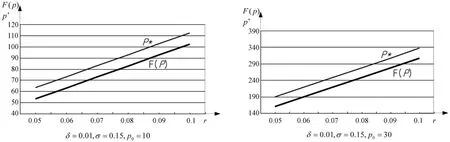
图3 无风险利率r与期权价值F(p)和临界值p*模拟曲线

四、土地供应政策的启示

从地方政府的公共服务职能来看，假定土地出让收入单纯用于公共支出产生社会效益(包括公共基础设施建设和保障性住房建设)，在此，期权价值F(p)泛化为经济价值和社会价值。

启示之一：不确定性σ来源于土地市场行情的不确定性，不确定性越大，土地开发商囤积土地可能性也越大，政府土地供应等待也越有价值(包括经济价值和社会价值)。理由是：(1)在不确定性环境下，土地开发商面临的风险越大，越不会急于开发，前期供应的土地囤积于开发商手中，表明市场土地量充足，不能继续供应土地;(2)在不确定性环境下，政府持续持有土地，供应时机和供应结构才能留有灵活性调整的机会。一旦单纯考虑财政收入，土地大量供应市场，此时倘若遭遇市场出现危机或需要保障性住房用地时，地方政府无地可供。因此，在市场行情不确定性较高的情势下，政府应持续持有土地，而不是卖空。

启示之二：由于机会损失 δ存在，期权价值F(p)随δ发生变化。土地市场δ越大，市场行情看跌，土地供应等待的期权价值下降，土地储备量就应减持，减少征地和拆迁。

启示之三：无风险利率r提高，则期权价值F(p)增加，因而临界值p*提高，意味着开发商购买土地价格提高，而土地储备中心降低土地购置成本的现值，却不影响政府土地供应的纯收益。因此，通过土地供应政策结合利率调整来调控土地市场，对开发商影响较大，对政府土地纯收益影响较小。

综上所述，地方政府要根据市场行情调节土地市场供求关系，选择恰当的土地供应时机，在保证经济价值和社会价值实现的前提下高效利用土地，兼顾土地所有权收益、土地开发商的经济利益和居民的社会福利。

［1］丰雷，苗田，蒋妍.中国土地供应管制对住宅价格波动的影响［J］.经济理论与经济管理，2011(2)：33-40.

［2］任超群，张娟锋，贾生华.土地供应量对新建商品房市场的影响——基于35个大中城市的实证研究［J］.软科学，2011，25(5)：1-4.

［3］丁洪建.土地供应政策对城市居住用地市场的影响机制及程度分析［J］.中国房地产，2010(4)：41-43.

［4］王兴，杜新波，杨景胜.土地宏观调控的机制框架与对策研究［J］.资源与产业，2011，13(2)：57-61.

［5］张红霞，谭术魁.城市土地市场调控政策工具的时滞研究——以武汉市为例［J］.中国土地科学，2010，24(1)：50-55.

［6］杨春鹏.实物期权及其应用［M］.上海：复旦大学出版社，2003：15-23.

［7］张金明，刘洪玉.实物期权与土地开发决策模型［J］.土木工程学报，2004，37(5)：92-95.

［8］刘涛.基于噪声实物资产的房地产开发调控政策［J］.系统工程理论与实践，2009，29(9)：58-63.

［9］刘涛，刘丽霞.基于实物期权的土地转化开发决策研究［J］.数学的实践与认识.2009，39(13)：56-63.

［10］GRAEME G.House prices，development costs，and the value of waiting［J］.Journal of Urban Economics，2010，68(1)：56-71.

［11］JEAN-DANIEL M S，MARLON G B.Uncertainty and the timing of an urban congestion relief investment：The noland case［J］.Journal of Urban Economics，2006，59(2)：189-208.

［12］CHRISTOPHER R C.House price uncertainty，timing of development，and vacant land prices：Evidence for real options in Seattle［J］.Journal of Urban Economics，2006，59(1)：1-31.

［13］王家华.高技术投资决策的期权方法与应用研究［M］.北京：中国金融出版社，2009：57-68.